简论数学符号语言的特征

摘 要：数学符号语言与其他语言相比，有其独特鲜明的特征，主要表现为符号的统一性和简洁性以及语义的确定性。不仅便于记录和阅读，而且更能加速思维的进程和高效传播，它打破了国界，成为了“最具公共语言的一门学科”。数学符号语言体系的形成和发展，促进了数学研究和数学知识的传播，同时也把人类语言学推向了新的高度和广度。

关键词：数学 符号语言 特征

语言是人类最重要的交际工具，与人类思维有着密切的联系，是人类思维和表达思想的手段，也是人类社会最基本的信息载体。人们借助语言保存和传递人类文明的成果[1]。人类语言有三个关键要素：信息、思维和思想。任何信息只有赋予语义，形成概念，经过形式化处理进行信息加工，通过思维形成思想，才能达到交流的目的。从这个意义上说，人类的语言也可以理解为人的思维为着交际的目的而传输的可供感知的信息。随着人类进化的演进发展，人类语言的形式也逐渐多样化，从语言的“信息传递”表现方式来分析，人类使用不同的器官和工具来表达思想，有了以声音为载体的声音语言，典型的为人类的口语、音乐等；通过肢体动作表现的肢体语言，如人的表情、手势语、体态语等，比较典型的是聋语；以图形、文字和符号为载体的书面语言，这类语言表达和保存的人类思想已蔚为大观，构成了人类现代文明的基础，形成了不同的学科。

数学是一门古老的学科，我国古代的“六艺”中就有“数”，属于人类书面语言中的重要组成部分。伽利略说过，数学是上帝用来书写宇宙的文字。基于这种理念，美国天文学家、科普作家卡尔·萨根认为，宇宙中的文明无论差异多大，都有一种共同的语言——数学语言，为此，还把数学语言作为宇宙语言的首选。数学语言也有文字语言、图像语言和符号语言之分。本文中的数学符号语言是指在数学中用以表示数学概念、数学关系等的符号和记号。包括表示数学概念的符号，表示数学关系和数学推理所使用的符号，以及其他专用符号等。数学通过符号语言传递现实世界中的数、量、关系及其空间形式。

数学符号语言是为适应数学思维特殊需要而出现的，它通过把具体事物“一般化”后用抽象的数字、字母、图形、关系式等保存和传递数学研究的成果，建构数学的知识大厦。数学发展到今天，已成为一个符号化的世界，闯入这个世界，处处都要和符号打交道，符号就是数学存在的具体化身。因此，数学符号是数学科学专门使用的特殊语言，是含义高度概括、形体高度浓缩的一种科学语言，也就是说，它是一种便于记录和阅读、加速思维进程和高效传播思维的科学书面语言，其作用不仅促进了数学研究的发展和数学知识的传播，同时也把人类语言学推向了新的高度和广度。

数学符号语言有以下三个主要特征：

一、符号的统一性

符号的统一性是数学符号语言的一大特征。无论什么国家的人，无论操用哪个国家和地区的语言的人看到a+b=b+a，都知道这是乘法交换律，这种数学约定或数学符号不仅展示了数学符号语言的全球统一性，更表达了数学思维“一般化”的过程。这里的“a+b=b+a”实际上是“32+56=56+32”“148+91=91+148”等无数个加法算式的“一般化”表达。

2014年微信上流行一个段子：“手机尾号暴露了你的年龄”。个中秘密，从数学的视角理解其实是一个数学语言的统一化和数学思维“一般化”的过程。

一旦把微信中的日常语言（见左栏）改用数学特定的符号语言来描述（见右栏），秘密就暴露无疑了。

微信中的要求： 用数学符号语言表达：

看一下你手机的最后一位 设手机的最后一位为x

把这个数字乘上2 2x

然后加上5 2x+5

再乘以50 （2x+5）×50

把得到的数目加上1764 （2x+5）×50+1764=100x+2014

用这个数目减去你出生那一年 100x+（2014-出生那一年）

得到的三位数，第一位是你手机的最后一位 百位上的数字是x，

最后两位就是你的实际年龄 （2014-出生那一年）

从右边那栏用数学符号语言表达的“一般式”中可知，后两位当然就是你的实际年龄了。“手机尾号暴露了你的年龄！”这个“神秘”的段子，在数学符号语言体系中就现出了“原形”，年龄是利用数学知识“计算”出来的，而不是“算命先生”算出来的。

把日常语言转化成数学符号语言，能揭示事物的本质属性，数学的魅力也就在这里。如对于上述左边的“日常语言”，不懂中文的人是“看不懂”的，但对具有初中文化程度的任何国家的人都能从右边的“数学符号语言”中知道其含义。因此，数学可称之为“最具公共语言的一门学科”[2]。

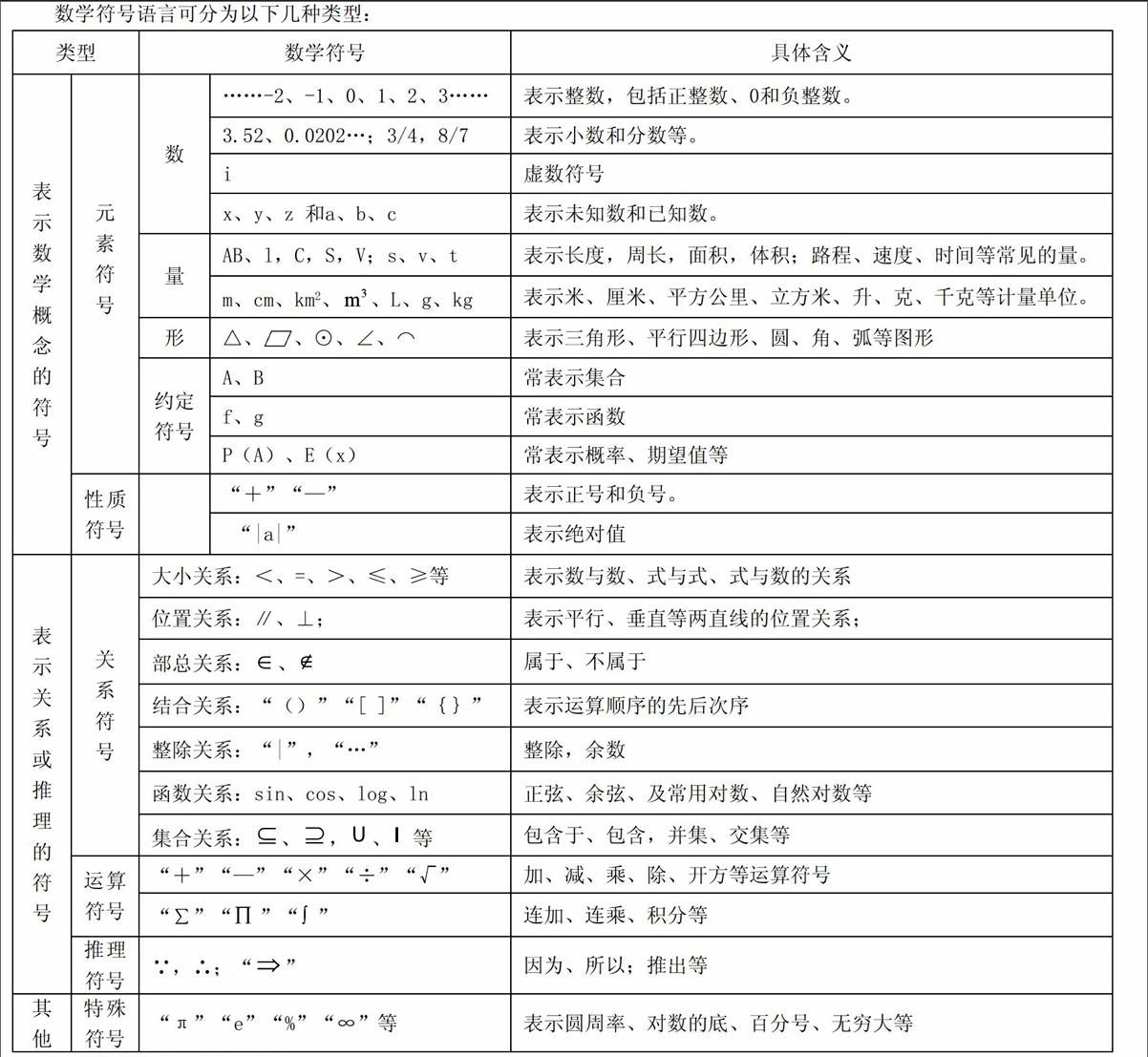
数学符号语言可分为以下几种类型：

这些符号都具有国际通用性。

数学符号语言的统一性，还体现在各国对数学的理解上。笔者曾让中国大陆和新加坡教师用图像语言描述数学老师，大家都不约而同地用“教‘1+2=3的图片”来描述数学老师的形象，也说明了数学符号语言的国际通用性。

数学在近两个世纪中取得了显著的进展和辉煌的成就，尽管有着许多因素，但数学符号语言的统一性厥功至伟。通过数学符号语言传达数学思想，简化思维过程，推动了数学自身的发展。

二、符号的简洁性

求简是数学的价值追求。回顾数学发展的历史，不难发现，为了更简洁、更容易书写、更便于理解和交流，经过一代又一代人的努力，数学符号从“1、2、3、4，+、-、×、÷”等记录数及其运算，“△”“⊙”“⌒”，“∥”“⊥”等描述空间图形及其关系到等 ，解决“无限”及其运算问题，经历了漫长的符号创造过程，如加号“+”和减“-”，直到1489年，在德国人约翰内斯·韦德出版的《适合所有商业的漂亮敏捷的计算法》一书中首次出现后才慢慢在全球范围内统一使用这个简单明确的符号。

再来看求和符号“∑”。通过“”把“1+2+3+……+99+100”这么长的连加算式用一个符号“”表示出来了，而且通过∑前后上下各个符号的变化可以表达更复杂的代数运算式，如等，如果用文字语言，不知要化多少篇幅，才能表达清楚。

这一点，从文字代数与符号代数的比较中也可以看得很清楚。今天看似十分简单的代数式“（10+x）2=100+20x+x2”，古代用文字表达则要叙述为“如果要求10和根自乘的结果，就要施行如下运算过程：10乘10得100；根乘10等于10个根；10乘根等于10个根；根乘根等于平方。总之，这个自乘的结果等于100，20个根和根平方”，多么冗长。古代人掌握简单的数的概念需要经历非常漫长、艰难的过程，而今天小学一年级的学生不仅能很快理解初步的数的概念，并且能掌握100以内的加减运算等，究其原因，除了古今人们实践和认识的条件不同外，十分重要的一个原因就是今天已有了一个规范统一简洁的数学符号语言系统。

数学符号语言的简洁性还表现在表达思想和推理过程的简洁与明了中。如定理“在有余数的除法里，如果被除数和除数能被同一自然数整除，那么，余数也能被这个自然数整除”，我们可用数学符号语言表示为：

如果a÷b=q…r，且d|a，d|b，那么，d|r

证明：∵a÷b=q…r，

∴a=bq+r

∵d|b

∴d|bq

又∵d|a，∴d|（bq+r）

∴d|r

这个定理的证明过程用数学符号语言表达，思维清晰，符合逻辑，能让读者一目了然地看到推理的过程。

三、语意的确定性

数学符号语言还具有语意确定性的特点，数学符号语言的语意是确定无疑的，思想是上下一贯、有根有据的。爱因斯坦曾说：在描述各种关系时要尽可能达到最高标准的严格精确性，这样的标准只有用数学语言才能做到。

许多数学符号的产生与发展也充分证明了这一点。如，最初是捷克的鲁道夫于1525年出版的《常用代数技巧规则下的速算》一书中使用符号“√”，后来笛卡儿添上一横线变成后才作为数学上的通用符号。有了这一横，就可以把谁的平方根看得一清二楚，避免语义上的混乱。

数学符号中虽然也有同一个符号语意不同的情况，如[ ]，它既可以表示中括号，也可以表达闭区间，又如加号和正号等，但它们使用在不同语境中，语义是非常明确的。

即便是界限模糊的一些概念，数学上也要想方设法，使之语义确定。如人们平时说的胖与瘦、高与矮，他们的界限是模糊的。《红楼梦》中用文学语言对“瘦弱的林黛玉”着墨很多，但100个人的心中有100个不同的“林妹妹”形象，这是文学语言的魅力。针对林妹妹“瘦”到什么程度的问题，如果用数学语言来表达，就是要确定什么是“瘦的”。假设40千克以下的人是“瘦的”，那么41千克是“瘦”还是“胖”呢？

“秃头悖论”也反映了这个问题。如果我们事先约定，头发根数不超过某一确定的常数n的人为秃头，那头发根数为n+1的人是否是秃头？根据约定，应该不算是秃头，但他只比头发根数为n的人多了1根，这样定性实在有悖常理。但如果约定，当N=n时为秃头，则N=n+1也为秃头。如此，根据数学归纳法，可以推得世界上所有的人都是秃头。显然，这是更加荒谬的结论，但推理的过程没有错呀！问题的根源在于“秃头”这个概念本身的语义模糊不清。

美国控制论专家L·A·查德通过研究数学的基础——集合论，发现普通集合论是扬弃了模糊性而抽象出来的。如一个对象a或者有某种性质，或者没有，即a要么属于集合A，要么不属于A，两者必居其一，而且只能居其一，决不容许模棱两可。用数学符号语言表示就是：

这是一个函数式，这个函数的值域是集合{0，1}。但查德认为，客观事物之间界限不分明的中介状态是普遍的，为此他对普通集合进行了推广，把点集改造为区间[0，1]，用介于0、1之间的一个数来说明该人的体重“多大程度上属于瘦的”，程度越高，这个数就越大。如设体重小于40千克的人是瘦子，其属于“瘦子”的程度（数学上叫做隶属度）为1，体重为60千克的人不是瘦子，其属于“瘦子”的程度或隶属度为0，那么，体重为a千克的人属于“瘦子”的隶属度就可以通过数学符号语言g（x）=（60- x）/（60-40），x[40，60]表达出来。如当x=50时，g（x）=0.5，当x=45时，g（x）=0.75，通过这个隶属函数g（x）就可以比较谁更“瘦”一点，显然45千克的人比50千克的人更“瘦”一点。这个隶属度在我们的生活中并不陌生，说“某事有80%的把握”，这里的80%，就是隶属度，这是模糊数学所研究的内容。模糊数学“硬”是把界限模糊的量用“数据”表示出来了，让这些概念的语义确定，关系明确不含糊。

由此可见，数学符号语言具有严密性和确定性的特点，能更加完善、准确、明了地把概念传递给人，它摆脱自然语言的多义性，避免了在推理中产生歧义而造成逻辑上的混乱。如果说文学语言、图像语言在传达思想时的模糊性和内省性，是为了表达人丰富的内心和情感世界，那么数学符号语言的确定性，则把人类的思维和推理过程表达得清楚明白，合乎逻辑。英国著名哲学家、数学家罗素说过“数学就是符号加逻辑”。

物理可以用实验解决问题，但数学必须用“数据”和“一般化”的论证。哥德巴赫猜想至今尚未解决就是因为没有找到“一般化”的论证方法。用简洁统一的符号、确定无误的概念进行推理和论证，这既是数学符号语言的特征，也是数学学科本身的特征。数学通过数学符号语言保存和传递数、量、关系和空间形式，并通过符号语言加速思维的进程，高效传播思维和数学思想方法。

（本文是教育部人文社会科学研究规划基金项目[项目批准号：11YJA880086]研究成果之一。）

参考文献：

[1]辞海编辑委员会.辞海[Z].上海：上海辞书出版社，1990：447.

[2]吴晓红，郑毓信.从质疑到释疑：数学教育国际比较可比性解读

[J].比较教育研究，2007，（8）.

[3]孟艾菊，娄亚敏.数学符号语言和自然语言的关系探微[J].现代

语文（语言研究版），2014，（3）.

[4][日]黑木哲德著.数学符号理解手册[M].赵雪梅译.上海：学林

出版社，2011：8.

[5]郑毓信.数学思维与小学数学[M].南京：江苏教育出版社，

2012：9.

（沈丹丹 浙江宁波 宁波大学教师教育学院 315211）