基于对偶树复小波变换的模糊图像质量评价*
2015-09-22杨蔚蔚
刘 婧,王 威,李 骥,杨蔚蔚
(长沙理工大学计算机与通信学院,湖南 长沙 410114)
基于对偶树复小波变换的模糊图像质量评价*
刘 婧,王 威,李 骥,杨蔚蔚
(长沙理工大学计算机与通信学院,湖南 长沙 410114)
小波域和结构相似度SSIM的质量评价方法已经成为图像处理领域的研究热点,然而都存在一定的缺陷:传统的离散小波变换缺乏平移不变性,其方向选择性也十分有限;对于严重模糊的图像,SSIM评价结果并不十分准确。基于此,提出了一种适应于模糊图像质量评价的新算法。该算法用对偶树复小波变换DTCWT将图像进行分解来获取复小波系数,然后对所得到的六个方向的高频子带系数分别进行平均梯度幅度值的结构相似度 MGSIM测量,最后将所得到的全部 MGSIM的均值作为最终的原始模糊图像的模糊值。仿真实验验证了本方法比结构相似度更吻合人眼的视觉效果,与主观评价方法具有很好的一致性,并且在各方面的性能都优于目前有关文献的方法。
小波域;对偶树复小波变换;SSIM;平均梯度幅度值的结构相似度(MGSIM)
1 引言
在图像处理过程中,如何对图像处理结果进行质量评价是一个值得重点关注的问题。模糊性是图像最常见的失真类型之一,导致图像失真的原因有多种,如光学系统的像差、相机与物体间的相对机械运动等。由于模糊图像的广泛存在,所以对模糊图像质量评价算法的研究具有非常重要的意义。当前经常使用的评价方法可以分为主客观这两种常见的类型。其中可信度最高的评价方法是数字图像的主观评价DMOS(Different Mean Objective Score)方法[1],主观评价方法通常会进行大量重复实验,不仅耗时多、费用高,并且无法建立对应的数学模型,脱离人工不能得到结果,因此不能应用到实际的视频和图像处理系统当中[2]。所以,图像质量的客观评价方法目前已成为研究的热点[3]。依据对原始图像的参照程度,客观图像质量评价可分为三类:全参考质量评价、半(弱)参考质量评价以及无参考质量评价[4]。在许多环境下,参考图像无法获取,因此需要深入研究无参考质量评价方法。
Feichtenhofer C H等人[5]根据人类视觉系统特性提取模糊图像边缘的梯度特征来建立 PSI (Perceptual Sharpness Index)指标,通过PSI指标直接计算图像质量;Ferzli R等人[6]采用恰可察觉模型JNB(Just Noticeable Blur)对模糊图像进行质量评价;Marziliano P等人[7]利用图像中的边缘平均宽度作为图像模糊测度,方法简单易行,可以取得更好的评估效果,Moorthy K A等人[8]提出先用分类算法求出失真概率,再单独计算失真强度并加权和等。以上都是从一定角度出发,构造了模糊图像质量评价指标,取得了一定的成果。但是,评价结果存在一定的缺陷,还需要进一步提高和改善,例如文献[5]的方法要求一次性先定义大批参数来进行失真概率的学习。
结合上述分析,本文提出了一种基于对偶树复小波变换和平均梯度幅度值结构相似度 MGSIM (Mean Gradient magnitude based structure SIM-milarity)相结合的模糊图像质量评估方法,先将图像进行对偶树复小波变换分解,针对六个方向的高频子带系数进行平均梯度幅度值的结构相似度测量,然后将所得到的全部 MGSIM的均值作为最终的原模糊图像的模糊值。
2 结构相似度计算
2.1 由模糊图像得到参考图像
原始无失真图像在经过高斯低通滤波器后可以得到一幅模糊图像,所得到的图像模糊程度是由低通滤波器的带宽来决定的。经过对原始无失真图像、模糊图像和滤波器使图像模糊的研究,发现人类对模糊值变化较小的图像之间的差异难以察觉。
自然图像a在经过11×11并且σ=1.5的高斯低通滤波器以后得到模糊图像b,同样的原理,把模糊图像b也经过相同高斯滤波器之后可以得到再模糊图像c。全参考图像质量评价中,必须要有清晰图像a作为参考,才能去评价模糊图像b的好坏。根据前面分析,如果没有清晰图像作为参考图像,那么可以用再模糊图像c作为模糊图像b的参考图像。因此,对模糊图像b的无参考图像质量评价问题,就转化为以模糊图像c作为参考图像的全参考图像质量评价问题。与模糊图像相比,清晰的图像包含有更详细的信息,即高频分量,所以可以通过高斯低通滤波器构造模糊图像c。
2.2 SSIM计算
图像与图像之间的像素差异即图像的高度结构性,用人眼直接观察时容易被忽略。考虑到多方面问题Zhou Wang等人[9]提出了一种新的结构相似度SSIM(Structural SIMilarity)图像质量评价方法。
SSIM包含了自然图像和失真图像分别在亮度、对比度以及结构信息各方面的对比,这三部分均可由单独的函数来表示,通常使用的计算方法如下:
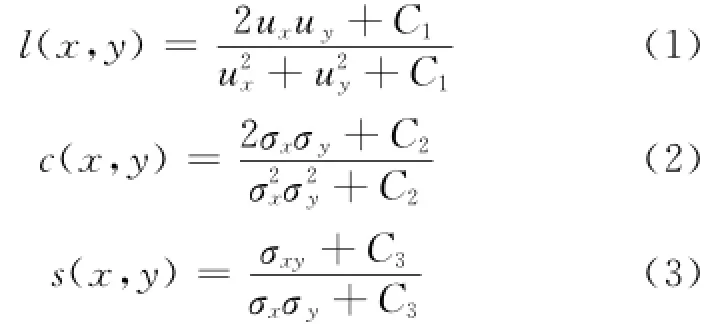
综合以上计算结果,可以得到模型的评判方法[10]:

其中,x为自然图像,y为质降图像,ux和uy为自然图像与质降图像中局部像素块的平均亮度值,σx和σy则表示为两幅图像中局部像素块的量度标准差,σxy为两幅图像中对应像素块的亮度相关系数。参数α、β、γ均大于零,以调整三个部分所占的比重,一般都取1;C1、C2、C3用于增加计算结构的稳定性,C1、C2、C3为较小的值。MSSIM(Mean Structural SIMilarity)算法将一幅图像划分成M个图像块,每一个图像子块的大小统一为N×N。由此整幅图像的MSSIM定义为:

2.3 MGSIM计算
虽然SSIM可以用来作为一种检测图像质量好坏的指标,但是对于严重模糊图像评估结果SSIM可靠 性 不 高[11,12]。人 类 对 图 像 的 边缘 信 息部分极度敏感,梯度能够很好地显示对比度和细节等不易察觉的图像纹理特征的变化,能够更好地评估图像的质量好坏,因此可以把梯度看成图像的重要结构信息,进行基于梯度的结构失真的图像质量评价方法[13]。
梯度幅值可以采用以下公式计算:

在图像质量评价中我们研究的是数字图像,对于数字图像一般可以用差分运算代替微分运算。公式(6)可借用差分公式来近似代替:
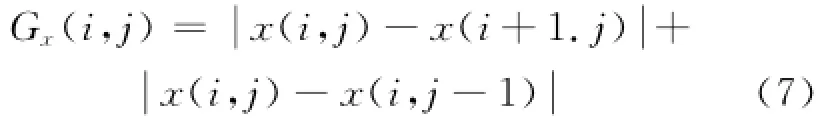
计算梯度的方法有很多,可用八邻域绝对值和来代表图像的梯度幅度值。图像x和y的梯度相似度g为:

其中Gx(i,j)、Gy(i,j)分别表示图像x和图像y在 (i,j)点的梯度幅度值。
将式(4)中的s(x,y)用梯度相似度g(x,y)代替,就可以得到GSIM。那么整个图像的梯度结构相似度可以由每一个子图块的GSIM的均值来求得:
设两幅图像x、y,xi、yi表示图像的子块,i∈[1,M],整个图像分块数为M,则:

MGSIM着重于图像之间细节上的相似度,因此更符合人眼视觉系统。
3 结合MGSIM和DTCWT无参考模糊图像评价算法
自离散小波变换DWT(Discrete Wavelet Transform)出现以来,它作为信号和图像处理的工具已经得到了一定的肯定,但是传统的离散小波变换存在缺少平移不变性和有限的方向选择性两个方面的弊端。
为了进一步克服离散小波变换所带来的弊端,Kingsbury N G在1998年提出对偶树复小波变换DTCWT((Dual Tree Complex Wavelet Transform)[14]这一新的小波变换,它是以离散小波变换为基础的一种新型小波变换模型,是二叉树算法的一种,不仅保留了DWT和CWT(Complex Wavelet Transform)的优点,而且还解决了其他小波变换的缺点,并且还具有更多比较好的优点,它有平移不变性和多方向性。
对偶树复小波变换是两个实值离散小波变换的和,它会得到±15°、±45°和±75°六个方向的子带,但是传统的离散小波变换只能够产生三个方向子带,分别是0°、45°和90°。一维的对偶树复小波变换分解公式如下:

其中,ζ表示一维向量,w(ζ)是尺度函数,φ(ζ)是扩散母小波,N是自然数集合,j和l分别是平移和扩散指数,Sj0,l是尺度系数,cj,l为复小波系数。
与一维对偶树复小波变换类似,二维对偶树复小波变换把二维图像Zα,β进行分解,分解如下:
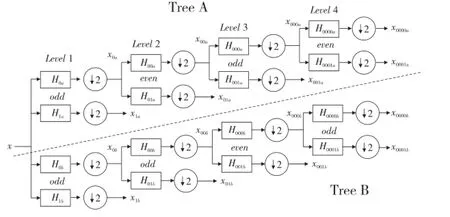
Figure 1 Principle diagram of the dual tree complex wavelet transform图1 对偶树复小波变换原理图

其中,θ∈Θ={±15°,±45°,±75°}是复小波函数的方向,这样就可以把Zα,β分解成一个复数的低通子带和六个复数值高通子带。
图1是DTCWT的详细图[15],该图给出了两个互相平行的小波树,即树A和树B。滤波器H0b和H1b与滤波器H0a和H1a之间的延迟恰好是一个采样值的间隔,那么就可以确保Tree B中的第一层的向下采样取到Tree B中因隔点采样运算而舍弃的不能保留的采样值。
在实现对偶树复小波变换的正变换后,还要实现其逆变换。为了实现其逆变换,我们在每棵树中都使用了双正交滤波器,这也是因为该滤波器的完全重构特性,同时为了达到整个系统近似的平移不变性,必须对最后两棵树所得到的结果求平均。经过二维对偶树复小波变换后,得到一个低频子带和六个方向的高频子带,方向分别是±15°、±45°和±75°,这么多的方向可以更好地描述图像纹理、边界等特征,可更好地用于图像后期处理。
4 实验结果与分析
4.1 实验流程
基于上述分析,模糊指标计算的具体步骤如下:
(1)为原图像构造参考图像。将原始模糊图像经过大小为11×11,σ=1.5的高斯低通滤波器得到再次模糊图像,作为参考图像。经过这一步就把原有的无参考图像质量评价转换成了全参考图像质量评价。
(2)提取对偶树复小波系数。将原始模糊图像和再模糊图像分别进行对偶树复小波变换得到± 15°、±45°和±75°的六个方向的子频带。
(3)MGSIM计算。把两幅图像得到的第i个系数分别进行平均梯度幅度值的结构相似度计算MGSIM(xi,yi)。
(4)对每一个频带的MGSIM求取平均值,获得整幅图像的平均梯度幅度值的结构相似度。最后将所得到的全部MGSIM的平均值等同于最后的评价图像的模糊值blur:

其中,N表示子频带个数;MGSIM表示每个子频带的平均梯度幅度值的结构相似度。MGSIM越大,所求的blur值越大,表示原始图模糊图像的质量越差,反之则质量越好。
本文方法的流程图如图2所示。

Figure 2 System flowchart图2 系统流程图
4.2 实验结果分析
实验选用LIVE实验室提供的blur图片库来验证本文方法的有效性(软硬件平台:PC;OS:Windows XP;CPU:2.71 GHz;RAM:2 GB;Software:Matlab 7.0)。选用两个客观参量作为评价指标,即经过非线性回归之后的皮尔逊相关系数CC(Correlation Coefficent)和斯皮尔曼等级相关系数SROCC(Spearman Rank Order Correlation Coefficient)。SROCC与CC是0到1的值,它们值越接近1,代表其性能越好。
为了对小波变换与对偶树复小波变换做深入比较,用Lena图进行了实验。图3为小波变换结果,图3a~图3c分别是90°、0°和高频结果图。图4为对偶树复小波变换结果图,图4a~图4f分别表示在方向—15°、—45°、—75°、75°、45°、15°的图像。对比两个变换后的结果,我们可以看出具有更多方向图像的对偶树复小波变换可以更好地描述图像在各个方向上的纹理特征。
图5a表示原图像,图5b~图5g分别是高频上方向为—15°、—45°、—75°、75°、45°、15°的变换结果。其中图5h是低频图像,因为低频图像很容易受到噪声、光照等因素的干扰与影响,所以它一般不用于图像质量评价中。
为了进一步评价本文方法的性能,本文算法与目前已有算法[5~7]的对比如表1所示。

Figure 3 Results after the wavelet transform图3 小波变换后结果

Figure 4 Results 1 after the dual tree complex wavelet transform图4 对偶树复小波变换后结果1
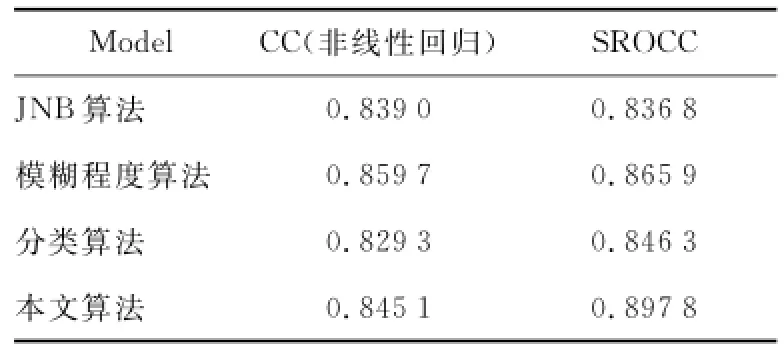
Table 1 Per formance comparison of different evaluation algorithms表1 不同评价算法的性能比较
由表1可见,与JNB算法、分类算法中的方法比较,本文算法的结果和主观评价方法的一致性、准确性都有比较明显的提升,相对于分类算法在CC评价值上提升了将近2个百分点,在SROCC上提升了5个百分点。把CC和SROCC这两个重要质量衡量指标结合起来思考,发现本文算法在一定程度上能够获得比较好的性能。
总之,由表1中的比较可以看出,本文中提出的方法预测的图像客观质量评价与图像主观评价更加一致,更加符合人眼视觉系统,而且计算复杂度低。因此,本文所提出的新方法可以用于对无参考模糊图像进行质量评价。

Figure 5 Results 2 after the dual tree complex wavelet transform图5 对偶树复小波变换后结果2
5 结束语
针对模糊失真图像,本文提出了一种基于对偶树复小波变换和平均梯度幅度值结构相似度相结合的模糊图像质量评估方法,通过高斯低通滤波将原始图像再模糊,对原始图像和模糊图像经过对偶树复小波变换和MGSIM等步骤,最终得到原始图像模糊值。实验结果表明,本方法是一种较准确可靠的无参考模糊图像评价方法。怎样把这种构造参考图像的评价方法应用到其他各种失真类型的无参考图像质量评价中将是以后工作的研究重心。
[1] Sheikh H R,Sabir M F,Bovik A C.A statistical evaluation of recent full reference in image quality assessment algorithms[J].IEEE Transactions on Image Processing,2006,15(11):3440-3451.
[2] Wang Hong-jiao.Research and implementation of the image quality assessment method[D].Xi'an:Xi'an University of E-lectronic Science and Techology,2014.(in Chinese)
[3] Lu W,Gao X B,Li X L,et al An image quality assessment metric based Contourlet[C]∥Proc of IEEE International Conference on Image Processing,2008:1172-1175.
[4] Wang Zheng-you,Li Zhen-xing,Lin Wei-si,et al.Improved image quality assessment model incorporating H VS and FSIM[J].Chinese Journal of Scientific,2013,33(7):1606-1612.(in Chinese)
[5] Feichtenhofer C H,Schallauer F H.A perceptual sharpness metric based on local edge gradient analysis[J].IEEE Signal Processing Letters,2013,20(4):379-382.
[6] Ferzli R,Karam L J.A no-reference object image sharpness metric based on just-noticeable blur[J].IEEE Transactions on Image Processing,2009,18(4):717-728.
[7] Marziliano P,Dufaux F.Winkler S,et al.Perceptual blur and ringing metrics:Application to JPEG 2000[J].Signal Processing:Image Communication,2004,19(2):163-172.
[8] Moorthy K A,Bovik A C.A two-step framework for constructing blind image quality indices[J].IEEE Signal Processing Letters,2010,17(5):513-516.
[9] Zhou Wang,Conrad Bovik.Image quality assessment:From error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.
[10] Li Ling-ling,Wang Hui,Yan Cheng-xin.Study on regional segmentation image fusion technique based on improved structure similarity[J].Application Research of Computers,2014(6):1914-1917.(in Chinese)
[11] Liu An-min,Lin Wei-si,Narwaria Manish.Image quality assessment based on gradient similarity[J].IEEE Transactions on Image Processing,2012,47(17):962-963.
[12] Gu Shan-bo,Shao Feng,Jiang Gang-yi,et al.An objective quality assessment metric for stereoscopic images based on just noticeable distortion[J].Journal of Optoelectronics Laser,2012,23(5):999-1004.(in Chinese)
[13] Yang Chun-ling,Kuang Kai-zhi,et al.Gradient based structural similarity for image quality assessment[J].Journal of South University of Technology,2006,34(9):22-25.(in Chinese)
[14] Kingsbury N G.Image processing with complex wavelets [J].Philosophical Transactions:Mathematical,Physical and Engineering Science(S1364-503x),1999,357(1760):2543-2560.
[15] Kingsbury N.Image processing with complex wavelets[EB/ OL].[2000-11-08].www-sigproc.eng.cam.ac.uk/publication/ngk/ngk99a.ps.gz.
附中文参考文献:
[2] 王洪娇.图像质量评价方法的研究及实现[D].西安:西安电子科技大学,2014.
[4] 王正友,李振兴,林维斯,等.结合 HVS和相似特征的图像质量评价方法[J].仪器仪表学报,2013,33,(7):1606-1612.
[10] 李玲玲,王蕙,闫成新.基于改进结构相似度的区域划分图像融合技术研究[J],计算机应用研究,2014(6):1914-1917.
[12] 顾珊波,邵枫,蒋刚毅,等.失真的立体图像质量客观评价方法[J].光电子·激光,2012,23(5):999-1004.
[13] 杨春玲,旷开智,陈冠豪,等.基于梯度的结构相似度的图像质量评价[J].华南理工大学学报,2006,34(9):22-25.

刘婧(1991 ),女,湖南益阳人,硕士生,研究方向为智能信息处理。E-mail:123410932@qq.com
LIU Jing,born in 1991,MS candidate,her research interest includes intelligent signal processing.
王威(1974),男,山东青岛人,博士,教授,研究方向为智能信息处理。E-mail:wangwei@csust.edu.cn
WANG Wei,born in 1974,PhD,professor,his research interest includes intelligent signal processing.

李骥(1981),男,湖南娄底人,博士,讲师,研究方向为信号处理和电磁散射。E-mail:hangliji@163.com
LI Ji,born in 1981,PhD,lecturer,his research interests include signal processing,and electromagnetic scattering.

杨蔚蔚(1988 ),女,湖南常德人,硕士生,研究方向为智能信息处理。E-mail:1732648392@qq.com
YANG Wei-wei,born in 1988,MS candidate,her research interest includes intelligent signal processing.
Blur image quality assessment based on DTCWT
LIU Jing,WANG Wei,LI Ji,YANG Wei-wei
(School of Computer and Communication Engineering,Changsha University of Science&Technology,Changsha 410114,China)
Wavelet domain and structural similarity(SSIM)quality assessment method have become hotspots in the field of image processing,however,both of them have some flaws:the traditional discrete wavelet transform lacks of translational invariance and its direction selectivity is also highly limited;for severe blurred images,the results of the SSIM are not very accurate.Therefore,we propose a new algorithm for blur image quality evaluation.This algorithm uses dual tree complex wavelet transform(DTCWT)image decomposition to obtain the complex wavelet coefficients and the high frequency sub band coefficients of all the six directions.Then the structural similarity of the average gradient amplitude is measured.Finally all the mean gradient-magnitude-based structural similarity(MGSIM)average is calculated as the final fuzzy values of the original blur images.Experimental results show that the proposed method fits the visual characteristics of human eyes better in contrast with the structural similarity method,and well matches the results of subjective evaluation methods.The assessment results are better than the current literature in terms of overall performance.
wavelet domain;dual-tree complex wavelet transform;SSIM;mean gradient magnitude based structural similarity
TP391.4
A
10.3969/j.issn.1007-130X.2015.08.023
1007-130X(2015)08-1573-06
2014-09-05;
2014-12-16
博士后基金资助项目(2013M542467);国防973基金资助项目
通信地址:410114湖南省长沙市长沙理工大学计算机与通信学院
Address:School of Computer and Communication Engineering,Changsha University of Science&Technology,Changsha 410114,Hunan,P.R.China
