基于小波阈值的非局部均值去噪*
2015-09-22李嘉浪李华君
李嘉浪,李华君,徐 庆
(天津大学计算机学院,天津 300072)
基于小波阈值的非局部均值去噪*
李嘉浪,李华君,徐 庆
(天津大学计算机学院,天津 300072)
非局部均值去噪算法充分利用了图像的全局信息,因此比传统的局部去噪算法有着更好的去噪效果。但是,非局部均值去噪算法计算时间复杂度较高,故利用小波阈值的方法对其进行改进,改进后使用非局部均值处理的数据量大幅减小。实验表明,改进后的算法比非局部均值算法去噪效果基本持平,且运行速度更快。
非局部均值;小波阈值滤波;图像去噪
1 引言
数字图像在获取和传输的过程中容易受到噪声的污染,被污染的图像会影响图像的进一步处理,对图像的理解和识别带来一定的困难。有效的去噪算法对后续的应用处理有着重要的意义。
图像去噪处理方法一般分为三大类:第一类是空间域法,比较常用的方法有高斯滤波法[1]、中值滤波法[2]和双 边滤 波 法[3]。第 二 类 是 基于贝 叶 斯最大后验概率推出的能量泛函模型。能量泛函包含两部分:数据模型和先验模型。比较常见的有马尔可夫 随 机场模 型[4]、熵 理 论[5]和几何 模 型 方法[6]。第三类是变换域的处理方法,将图像变换到频率域中进行处理,比较常见的方法有傅里叶变换和小波变换[7]。其中由于小波处理的独特优越性,近年来成为了图像处理的一个重要工具。
Buades A[8]针对空间域的加性噪声提出了非局部均值NLM(Non-Local Means)去噪模型。该算法主要采用全局搜索的方法,充分利用图像的冗余信息,得到图像每一个像素的灰度值。算法使用了块匹配的思想,从而增强了图像匹配的鲁棒性。由于该算法效果显著,在近些年得到了广泛的关注和改进。
Orchard J[9]提出将图像先映射成一个低维度的矩阵,缩短运算时间,同时降维矩阵保留了原图的主要特征。Tasdizen T[10]提出了基于主成份分析法的快速NLM去噪PNLM(PCA Non-LocalMeans)。先求出图像块的特征值和特征向量,将特征值按从高到低进行排列,然后取前六个特征值对应的特征向量,将图像块映射到这六个特征向量上。图像块降到一个低维度的矩阵,降低了时间复杂度;同时保留了图像的主要信息,故去噪效果与原NLM效果基本持平。Vignesh R等[11]提出阈值法,当块间距离超过阈值时,说明搜索块和待处理块的相关性较差,将其丢弃,以提高运算效率,同时加大相似块的权重,改进去噪效果。Brox T等[12]提出先进行图像分类,利用k均值算法将相近的像素划为一类,NLM只在相近的类中进行计算,减少计算的时间。Van De Ville D等[13]将均方误差作为目标函数,当均方误差达到最小时相应的参数设置为NLM的最优参数。Mahmoudi M[14]使用像素块的平均值和梯度值作为评价像素块相似的标准,对于不相似的像素块及时丢弃。文献[15]在NLM权重计算过程中用1范数代替2范数,从而使得边缘更加清晰饱满。Sun Z[16]对文献[15]进行了改进,将两个块相似度的计算改为p范数(0<p<1)。
本文针对NLM时间复杂度较高的问题,提出将小波阈值和非局部均值去噪进行结合的方法,将图像进行两层小波分解。对于第二层的低频部分L2进行保留,第二层的高频部分使用小波阈值去噪。将处理后的第二层进行逆小波变换,得到第一层的低频图像L 1′。对L 1′进行改进的NLM处理,第一层的高频部分用小波阈值处理,最后进行小波逆变换得出去噪后的图像。利用小波特性,保留了图像的纹理特征,得到较好的去噪效果,并提高了算法的运行速度。
2 非局部均值去噪算法
图像噪声模型可以写为:
v(i)=u(i)+n(i) (1)
其中,u(i)代表着未被污染的图像的像素值,n(i)代表着噪声,v(i)代表着污染后图像的像素值。
非局部均值去噪中目标像素点的估计值是由图像中所有的像素点加权平均得到的,权重的大小是由两个以像素点为中心的像素块的相似度来决定的:
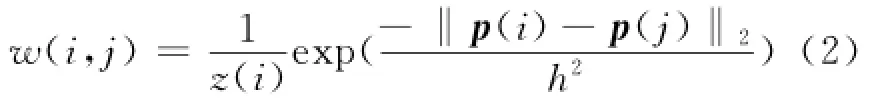
其中,z(i)的作用是实现权重的归一化,i是目标像素点,j是图像中所有的像素点。像素i和像素j的相似度依赖于灰度级矩阵P(i)和P(j)的相似度,P(i)是指以i为中心的n×n的像素矩阵块,n一般取7。P(i)和P(j)的相似度通过高斯加权欧式距离‖P(i)—P(j)‖2来表示。h为滤波参数,控制指数函数的衰减速度,即权重的衰减速度。
在遍历了所有的像素点后得出了图像中所有像素点对于目标像素点的权重,最后将所有像素点进行加权均值即可得到目标像素点的像素值:

其中,u(i)代表着i点的预测像素值,u(j)代表原始图像在j点的像素值。
3 小波阈值去噪
小波阈值去噪是小波去噪中比较有代表性的一种方法。小波去噪的实质是一个函数逼近问题:即根据衡量准则,如何在由小波母函数伸缩和平移展成的函数空间中,区分出信号和噪声,寻找对原信号的最佳逼近。小波阈值收缩去噪利用了小波变换中多分辨特性对特定信号的“集中能力”,即如果一个信号的能量集中于少数小波系数,那么这些系数值必然大于能量分散的噪声小波系数值。
小波阈值收缩法中,最为重要的是选择阈值和阈值函数。阈值太小,去噪后图像仍有噪声;相反,阈值太大,重要的图像特征将被滤掉,引起失真。直观上讲,对于给定的小波系数,噪声越大,阈值就越大。所以,大多数阈值选择过程是针对一组小波系数,根据其统计特性,计算出阈值。
本文小波阈值的选取主要采用的是Bayes shrink法,该计算公式如下:
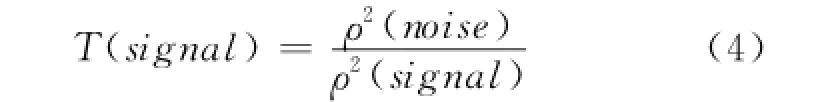
其中分母表示图像的信号方差估计,分子表示噪声的信号方差估计。当小波系数小于阈值时,说明信号受噪声的影响较大,故置为0;当小波系数大于阈值时,说明信号受噪声的影响较小,所以进行保留。
假设小波系数是 wj,k,变换后的 小波系数为w'j,k,u为小波阈值,软阈值和硬阈值函数表示如下:
软阈值法:

硬阈值法:
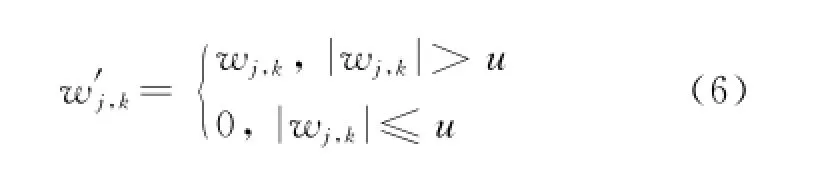
4 基于小波阈值的非局部均值去噪
图像在采集、转换和传输过程中受到成像设备和外部环境的干扰而产生噪声,这些噪声有一定的共同点,即在一定的频段会表现出一定的特征。小波变换是一种窗口大小固定但其形状可改变、时间窗和频率窗都可改变的时频局部化分析方法。经小波变换后图像的大部分能量多集中在趋势变换系数而不是波动系数。图像经小波变换后在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率。这种特性使得小波变换具有对信号的自适应性,能较好地分析处理信号的局部特性。
图像和噪声经过小波变换后表现出不同的统计特征,图像本身的能量主要集中在低频,与幅值较大的小波系数对应。噪声主要分散在小波变换后的高频部分,与幅值较小的小波系数相对应。故改进算法主要将图像进行多分辨率分解,在低频部分用改进的NLM进行去噪处理,而在高频部分则采用小波硬阈值的方法进行处理。
其步骤可总结如下:
(1)对一幅含有噪声的图像,进行二维小波分解。分解为低频图像L1和高频的细节信息图像H 1。
高频的细节信息又包含了三个部分:水平细节信息、垂直细节信息和对角细节信息。
(2)使用Bayes shrink法对高频图像H 1进行小波阈值去噪,得到H 1′。
(3)对L 1进行小波分解,分解为低频图像L2和高频图像H 2。
由于L1中噪声部分和图像信息混合在一起,并没有较为明显的区分。因此需要进行分解,需要分解的层数与图像质量和特性有关。通过实验得出分解到二层的时候处理效果已经达到处理要求。
(4)使用Bayes shrink法对高频图像H 2进行小波阈值去噪,得到H 2′。
第二次分解后的低频部分L2主要含有图像的整体信息,故不作任何处理;高频部分 H 2含有图像细节和噪声,使用小波硬阈值法进行噪声的过滤,得到H 2′。
(5)通过小波逆变换对L 2和H 2'进行重构。
(6)对(5)重构得到的低频图像使用改进的NLM去噪算法,得到图像L 1′。对NLM算法进行改进,即用每一迭代得出的新像素值取代对应原图的原始像素值,在下一次迭代时使用上一次迭代更新后的图像像素值,使得信息的提取更加准确。
具体步骤如下:
①对于L 1′中的每一个像素点i,计算图像所有像素值的权重w(i,j),权重的计算如下:
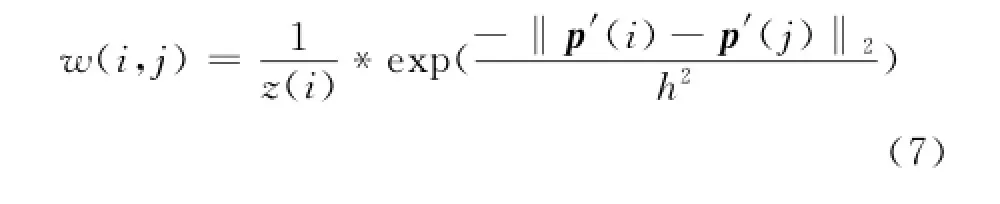
其中,P'(i)、P'(j)分别为更新后图像L 1′中以i和j为中心的像素块。
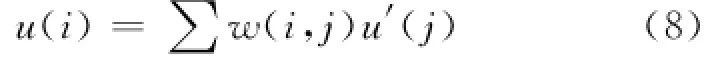
其中,w(i,j)为公式(7)中得到的各个像素点的权重,u'(j)为更新后图像L 1′中第j个像素点的像素值。
②更新L 1′中第i个像素点的像素值为u(i)。
(7)通过小波逆变换对H 1'和L1'进行重构,得到最终的输出图像。具体算法的流程如图1所示。

Figure 1 Denoising processing图1 去噪流程图
5 实验仿真结果
将改进后的NLM去噪和原始的NLM、小波阈值去噪以及PNLM进行比较。测试的图像采用国际标准RGB测试图像House和Pepper,大小是256×256像素。评价标准为峰值信噪比PSNR (Peak Signal to Noise Ratio)。添加的噪声为高斯白噪声,方差为30~50。实验结果见表1。
由表1可以看出,基于小波阈值的NLM去噪算法与原始的 NLM去噪算法相比,在σ较小时PSNR略有不及,但在σ比较大的时候,PSNR有略微反超。与小波阈值去噪算法相比,PSNR的提高比较明显。
图2为表1所列方法的处理结果图,实验中的噪声量σ为30。改进后的去噪算法的PSNR与NLM以及PNLM在处理效果的指标上基本持平。但是从肉眼观察来说,更符合人眼的视觉标准,且色彩更加饱和,边缘更加清晰。相比NLM原算法,基于小波阈值的NLM充分考虑了时间复杂度问题,使得NLM处理的数据量降低为原来的1/4。设图像尺寸为m×m,邻域图像尺寸块为n×n,权重的搜索窗口限定在t×t,其原始NLM计算的时间复杂度为O(m2·n2·t2),计算时间复杂度很大。基于小波阈值的非局部去噪算法将图像进行了两层小波分解,NLM算法主要在第一层的低频图像进行迭代。第一层的低频图像是原始图像的1/4大小,权重的搜索窗口限定为1/2t×1/2t,邻域尺寸不变,故在小波阈值分解后NLM处理的时间复杂度为O(1/16·m2·n2· t2)。
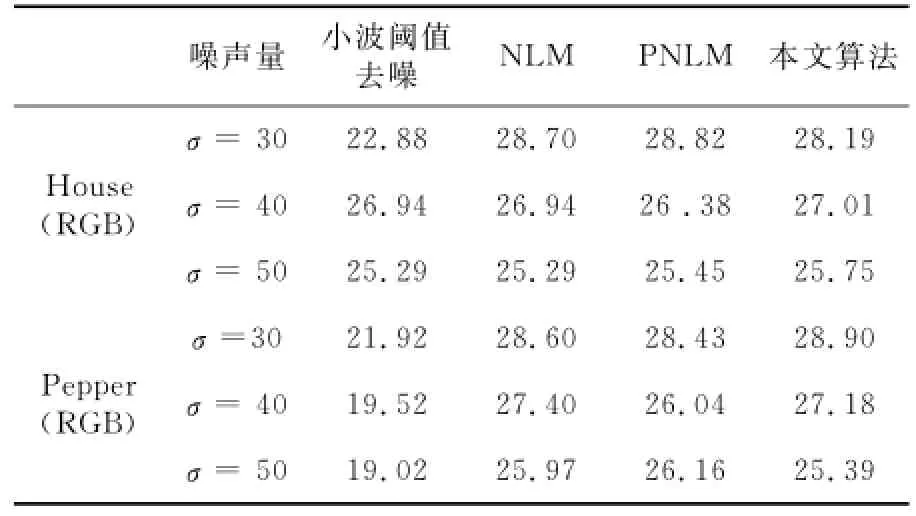
Table 1 PSNR comparison between the wavelet shreshold NLM and other methods表1 基于小波阈值非局部去噪与其它方法的峰值信噪比PSNR结果对比

Figure 2 Results of different denoised methods图2 不同方法对House的去噪结果图
将基于小波阈值的非局部均值去噪算法与原始的NLM、小波阈值去噪以及PNLM运行时间进行比较,实验结果见表2。由于本文所提出的算法分为二维小波分解、小波阈值去噪以及 NLM去噪,其中小波分解以及小波阈值去噪需占用一定时间,故实际的执行时间未达到原算法的1/16。以上的测试是在主频为Intel Core Duo 2.53 GHz、1 GB内存的计算机上得出的。

Table 2 Execution time comparison between the wavelet shreshold NLM and other methods表2 基于小波阈值的非局部均值去噪与其它方法的执行时间对比 s
6 结束语
本文提出了一种基于小波阈值的快速非局部均值去噪算法。该算法对图像进行了两层小波分解。对于第一层和第二层的高频部分使用小波阈值去噪,对于逆变换后第一层的低频图像使用改进的NLM去噪。通过实验证实了基于小波阈值的NLM算法,在去除噪声的同时更好地保持了图像的边缘信息,且相较其他NLM改进算法运行的时间大幅降低。
[1] Lindenbaum M,Fischer M,Bruckstein A.On Gabor's contribution to image enhancement[J].Pattern Recognition,1994,27(1):1-8.
[2] Ahmad M O,Sundararajan D.A fast algorithm for two dimensional median filtering[J].IEEE Transactions on Circuits and Systems,1987,34(11):1364-1374.
[3] Tomasi C,Manduchi R.Bilateral filtering for gray and color images[C]∥Proc of the 6th International Conference on Computer Vision,1998:839-846.
[4] Bremaud P.Markov chains:Gibbs fields,Monte Carlo simulation,and queues[M].Berlin:Springer,1999.
[5] Arias P,Caselles V,Sapiro G.A variational framework for non-local image inpainting[C]∥Proc of the 7th International Conference on Energy Minimization Methods in Computer Vision and Pattern Recognition,2009:345-358.
[6] Rudin L,Osher S,Fateni E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1-4):259-268.
[7] Chang S G,Yu B,Vetterli M.Adaptive wavelet thresholdingfor image denoising and compression[J].IEEE Transactions on,Image Processing,2000,9(9):1532-1546.
[8] Buades A,Coll B,Morel J M.A non-local algorithm for image denoising[C]∥Proc of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2005:60-65.
[9] Orchard J,Ebrahimi M,Wong A.Efficient non-local means denoising using the SVD[C]∥Proc of the 15th IEEE International Conference on Image Processing,2008:1732-1735.
[10] Tasdizen T.Principal components for non-local means image denoising[C]∥Proc of the 15th IEEE International Conference on Image Processing,2008:1728-1731.
[11] Vignesh R,Oh B T,Kuo C C J.Fast non-local means (NLM)computation with probabilistic early termination[J].IEEE Signal Processing Letters,2010,17(3):277-280.
[12] Brox T,Kleinschmidt O,Cremers D.Efficient nonlocal means for denoising of textural patterns[J].IEEE Transactions on Image Processing,2008,17(7):1083-1092.
[13] Van De Ville D,Kocher M.Nonlocal means with dimensionality reduction and SURE-based parameter selection [J].IEEE Transactions on Image Processing,2011,20(9):2683-2690.
[14] Mahmoudi M,Sapiro G.Fast image and video denoising via nonlocal means of similar neighborhoods[J].IEEE Signal Processing Letters,2005,12(12):839-842.
[15] Chaudhury K N,Singer A.Non-local Euclidean medians[J].
IEEE Signal Processing Letters,2012,19(11):745-748.[16] Sun Z,Chen S.Analysis of non-local Euclidean medians and its improvement[J].IEEE Signal Processing Letters,2013,20(8):303-306.

李嘉浪(1988),女,山西临县人,硕士生,研究方向为计算机图像处理。E-mail:542617751@qq.com
LI Jia-lang,born in 1988,MS candidate,her research interest includes computer image processing.

李华君(1989 ),女,湖南吉首人,硕士生,研究方向为计算机图形可视化。E-mail:411617428@qq.com
LI Hua-jun,born in 1989,MS candidate,her research interest includes computer graphic visualization.

徐庆(1969 ),男,天津人,博士,教授,研究方向为计算机图形学。E-mail:qingxu@tju.edu.cn
XU Qing,born in 1969,PhD,professor,his research interest includes computer graphics.
Non-local means denoising based on wavelet threshold
LI Jia-lang,LI Hua-jun,XU Qing
(School of Computer Science,Tianjin University,Tianjin 300072,China)
The non-local means denoising algorithm can use the globe information of the picture,therefore it has better denoising effect than other traditional algorithms.However,since its time complexity is high,we put forth a new non-local means denoising algorithm based on wavelet threshold filter,which use much less data than the traditional non-local means.Experimental results show that compared to the traditional non-local means,the denoising effect of our algorithm is basically the same,but the running speed is faster.
non-local means;wavelet threshold filter;image denoising
TP317.4
A
10.3969/j.issn.1007-130X.2015.08.019
1007-130X(2015)08-1546-05
2014-04-08;
2014-07-12
国家自然科学基金资助项目(U1333110)
通信地址:300072天津市天津大学计算机学院
Address:School of Computer Science,Tianjin University,Tianjin 300072,Tianjin,P.R.China
