GO法在软件体系结构可靠性分析中的应用*
2015-09-22贺慧琳
贺慧琳
(南华大学数理学院,湖南 衡阳 421001)
GO法在软件体系结构可靠性分析中的应用*
贺慧琳
(南华大学数理学院,湖南 衡阳 421001)
GO法是一种系统可靠性分析方法,可将GO法应用到软件体系结构的可靠性分析中。根据软件体系结构自身的特点及构件之间的关系,分别建立了软件体系结构六种基本结构的GO模型,并进行了定量GO运算。通过一个实例,说明了应用GO法对软件体系结构的可靠性进行分析的全过程。实践表明:运用定量GO运算能够方便地计算出整个软件体系结构的可靠度,通过定性GO分析还可评估各构件及连接件的重要性,对后期系统的设计与开发具有一定的指导意义。
GO法;可靠性分析;软件体系结构
1 引言
为了适应大规模、高复杂性软件的开发,20世纪90年代后,基于构件的软件开发技术被广泛应用,这是一种“构件开发+基于体系结构的构件组装”的开发技术[1],这种开发技术将体系结构的开发作为系统开发过程的一个关键性环节,它在软件需求与软件设计之间起到了桥梁的作用,软件体系结构SA(Software Architectures)的好坏将会直接影响到软件的质量。随着人们对软件质量的要求越来越高,软件的可靠性作为衡量软件质量的一个重要因素也受到了人们的重视。因此,对软件体系结构的可靠性分析实际上就是在软件开发早期对系统可靠性进行的评估,这使得人们能够尽早发现系统中可能存在的问题,不仅有助于提高软件的质量,而且对系统后期的开发具有一定的指导意义。
近年来,已有许多国内外学者对软件体系结构的可靠性进行了研究,并提出了一些基于软件体系结构的可靠性模型,如Yacoub模型[2]、Wang模型[3]和毛晓光通用模型[4]。这些现有的模型可分为两 类[5]:基 于路 径 的 模 型[2]和 基于状 态 的 模型[3,4]。基于路 径的 模 型 通常 根 据 软件 各 执 行路径的可靠性及执行概率来计算软件可靠性,容易出现路径无穷长问题[4]。而基于状态的模型通常假设构件的控制转移行为具有马尔科夫随机性,利用Markov链来描述构件的状态转移,但未对构件间的确定性转移行为进行分析,此外,当系统复杂性增加时,可能会出现状态空间组合爆炸问题。以上两类模型都没有考虑软件体系结构自身的结构特点,因此无法从组成软件体系结构的基本结构出发来指导软件体系结构的设计[6]。
GO法是一种以成功为导向的系统可靠性分析技术,多适用于有实际物流如电流的系统可靠性分析。GO法的主要步骤就是建立GO图和进行GO运算,它通过对系统的分析来构造相应的模型,这个模型称为GO图,通常可根据系统流程图、原理图或结构图来建立GO图。GO图主要由操作符和信号流组成,系统中的元件、部件或子系统可统称为单元,操作符可用来代表单元功能和单元输入、输出信号之间的逻辑关系;而信号流则用于连接操作符生成GO图,它表示系统单元的输入和输出以及单元之间的关联。GO法定义了17种标准操作符[7],操作符的定义及运算规则详见文献[7~9]。
对于软件体系结构的定义,目前学术界尚未形成统一的意见,但是,多数定义都强调了体系结构的基本要素是构件、连接件及其约束。其中,构件是指具有一定功能的软件单元,连接件是构件之间的连接单元,用于建立构件间的交互,约束确定了体系结构的构件与连接件的连接关系。因构件和连接件被用于构建系统或软件体系结构时所起的作用不同,构件与连接件不交;构件、连接件是一个体系结构,构件之间通过连接件经有限次连接后仍是 一 个 体 系 结构[10]。
文献[6]从软件体系结构自身结构特征出发,把整个软件体系结构看作是由六种基本结构嵌套构成的。本文基于文献[6]的理论,尝试用GO法及故障树法对软件体系结构的六种基本结构及整个软件体系结构进行可靠性建模,实现在软件开发早期对软件进行可靠性评估,并通过两种方法的对比说明GO法应用与软件可靠性分析的优缺点。
2 基本结构的可靠性分析
根据SA自身的特点及构件之间的关系,可以把整个SA看作是由顺序结构、与汇合结构、或汇合结构、与分支结构、或分支结构和迭代结构六种基本结构嵌套构成[6]。本节分别用 GO法和故障树法对这六种基本结构进行可靠性建模。
在GO图中,可用操作符代表构件和连接件,构件及连接件都有两个状态,若能正常工作即为成功状态,若失效则为故障状态,因此构件和连接件可用类型1操作符表示。GO图操作符中第一个数字表示操作符的类型,第二个数字表示操作符的编号,编号必须唯一,这里操作符及信息流的编号与构件、连接件的编号保持一致。
在故障树法中,可将构件及连接件的失效作为故障事件。
用GO图和故障树法分析软件体系结构可靠性的前提是必须已知构件和连接件的可靠性,通常可由构件开发者或供应商提供。
设PCi表示编号为Ci(即构件)的操作符的成功概率,PLi表示编号为Li(即连接件)的操作符的成功概率,PSi表示编号为i的信号流的成功概率,PR表示输出信号流的成功概率,PS表示系统故障概率。设置操作符0作为虚拟输入操作符,其成功概率为1,即P0=1。
(1)顺序。
顺序结构的SA如图1a所示。SA由n个构件组成,n个构件连续处理能够完成某个功能,当且仅当n个构件、连接件全部正常工作,系统才正常工作[6]。为顺序结构建立的GO图及故障树如图1b和图1c所示。

Figure 1 Serial software architecture,its GO chart and fault tree图1 顺序型SA及其GO图和故障树
定量GO运算根据文献[7~9]给出的各操作符运算规则,可得到各信号流成功概率的计算式:
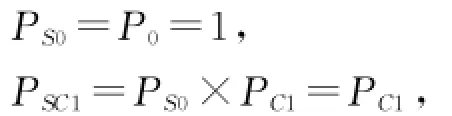
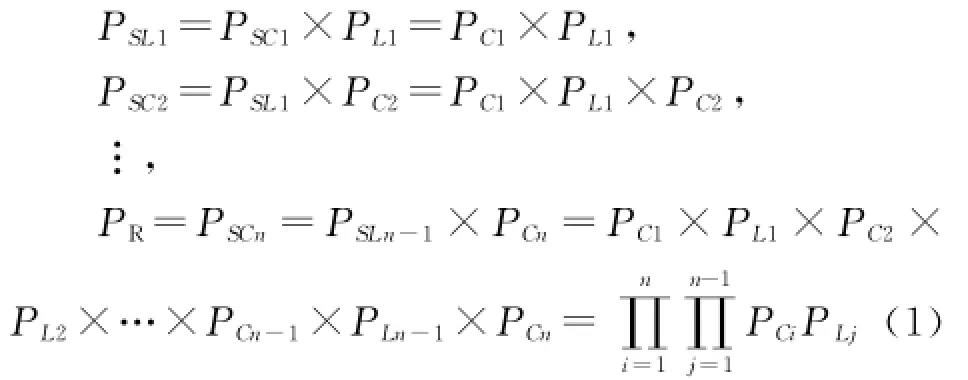
根据图1c所示故障树得到系统故障概率计算式为:
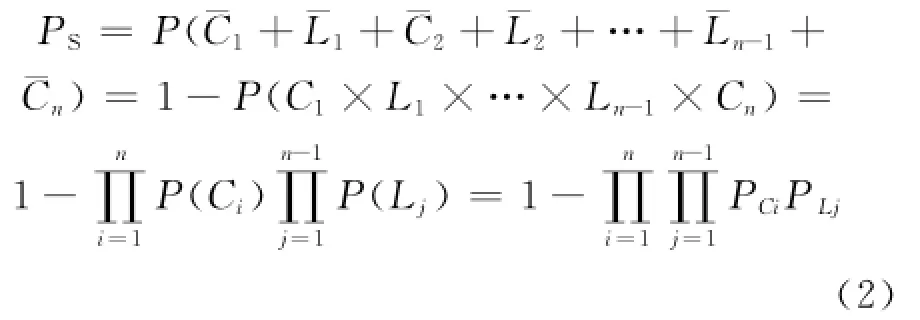
(2)与汇合。
与汇合结构的SA如图2a所示。SA由n+1个构件组成,由n个构件共同与某一构件协作来完成某个功能,当且仅当n+1个构件和n个连接件全部正常工作,系统才能正常工作[6]。n个构件之间的逻辑关系可用类型10与门操作符表示,为与汇合结构建立的 GO图及故障树如图2b和图2c所示。

同理可得信号流成功概率的计算式:,该公式与式(1)一致,表明由GO法

(3)或汇合。
或汇合的SA如图3a所示。SA由n+1个构件组成,选择n个构件中的任一构件和第n+1个构件协作就能够完成某个功能,即只要构件Ci、连接件Li和 构 件Cn+1正常 工 作 时,系 统 才 正 常工作[6]。n个构件之间的逻辑关系可用类型2或门操作符表示,为或汇合结构建立的GO图及故障树
由故障树求得系统故障概率计算式为:
如图3b和图3c所示。
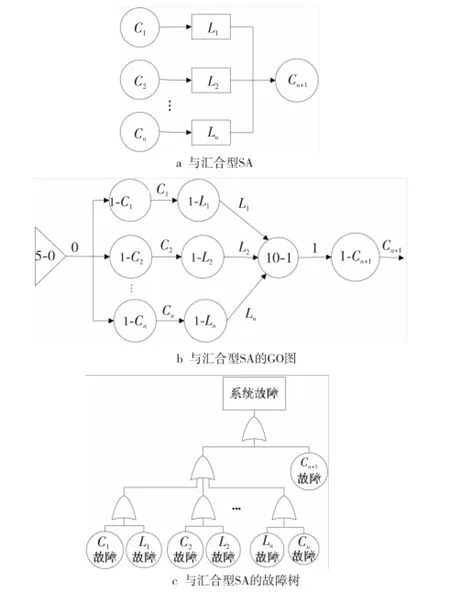
Figure 2 And confluence software architecture,its GO chart and fault tree图2 与汇合型SA及其GO图和故障树

同理可得信号流成功概率的计算式为:
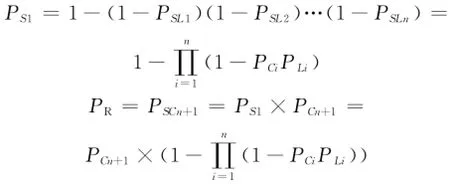
由故障树求得系统故障概率计算式为:

(4)与分支。
与分支的SA如图4a所示。SA由n+1个构件组成,要经过一个构件与n个构件共同来完成某个功能[6],系统正常 工 作 的 条 件是 构 件 C0和n条支路都正常工作。n条支路之间的逻辑关系可用类型10与门操作符表示,为与分支结构建立的GO图及故障树如图4b和图4c所示。
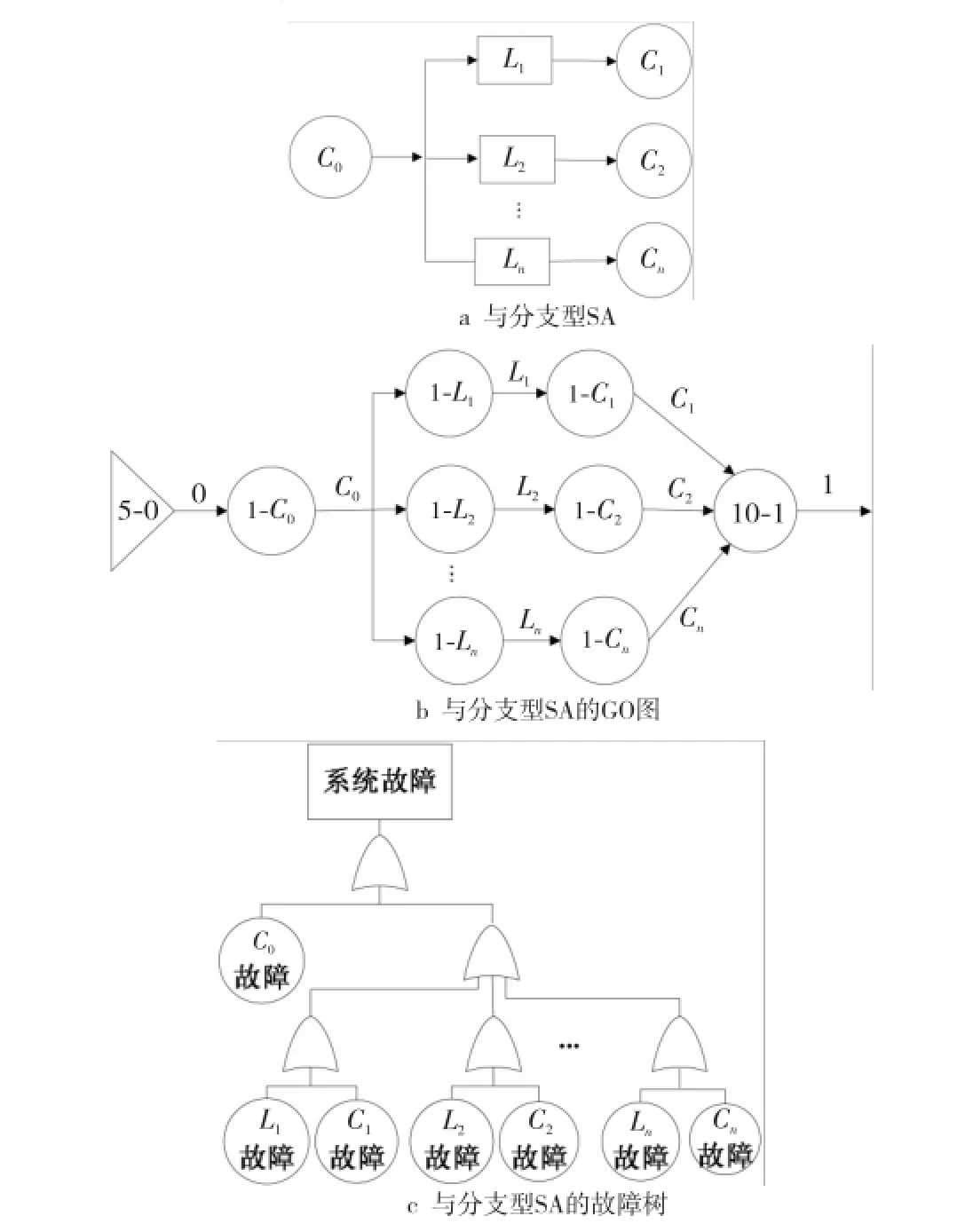
Figure 4 And branch software architecture,its GO chart and fault tree图4 与分支型SA及其GO图和故障树
同理可得各信号流成功概率的计算式为:
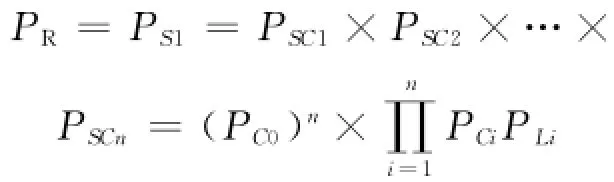
上式中信号流Ci(i=1,…,n)不独立,有共有信号C0,因此上式不成立,需要进行修正,根据文献[7]的方法,可用共有信号概率的一次项代替其高次项来进行简化,即是对共有信号项的修正,修正后的概率表达式为:
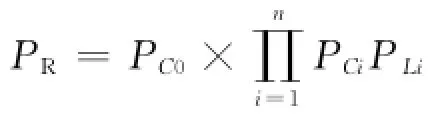

(5)或分支。
或分支的SA如图5a所示。SA由n+1个构件组成,经过一个构件与n个构件中的某一个构件共同来完成某个功能[6],系统正常工作的条件是构件C0能正常工作,且n条支路中至少有一条能正常工作。n条支路之间的逻辑关系可用类型2或门操作符表示,为或分支结构建立的GO图及故障树如图5b和图5c所示。
由故障树求得系统故障概率计算式为:
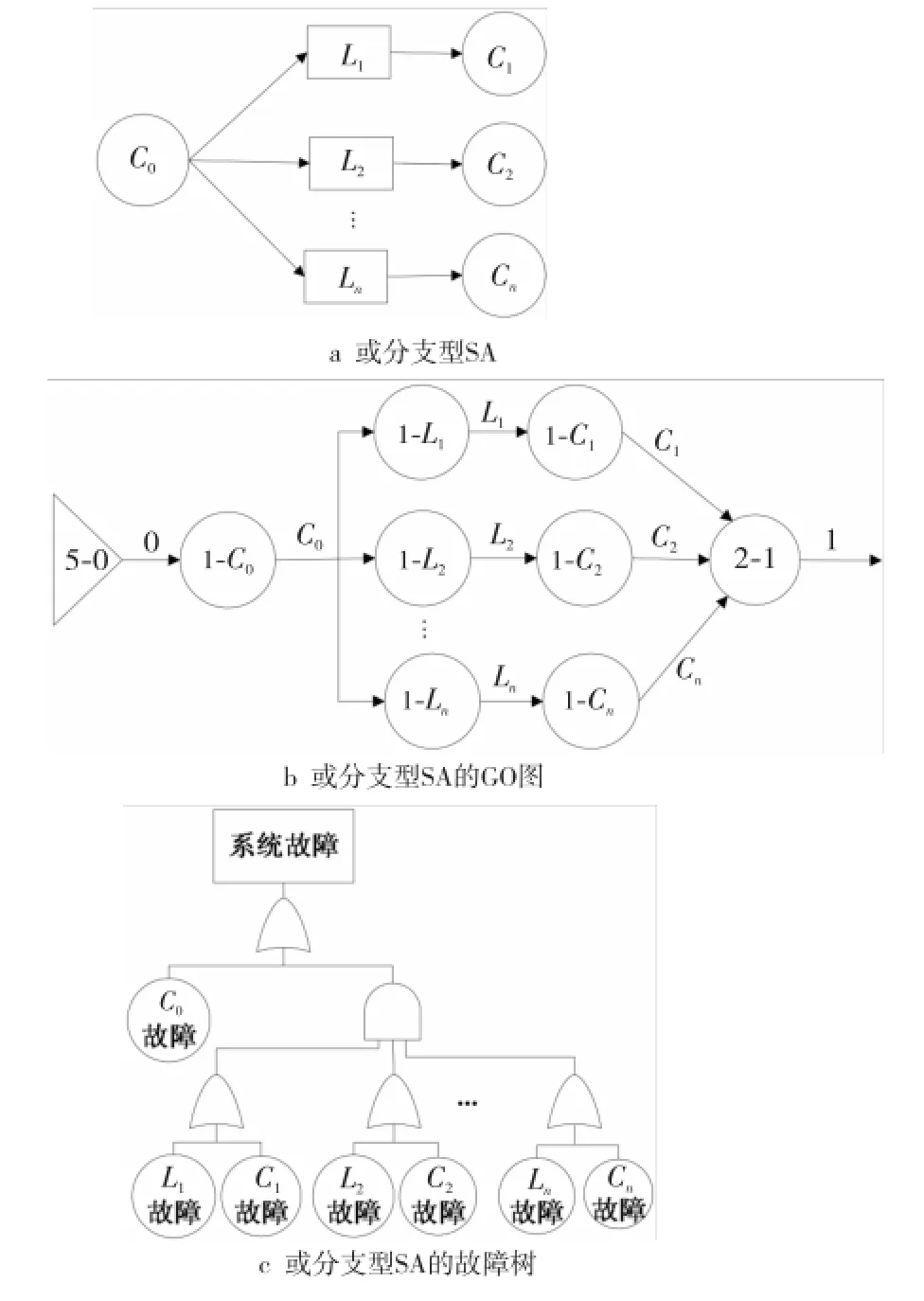
Figure 5 Or branch type software architecture,its GO chart and fault tree图5 或分支型SA及其GO图和故障树
此结构中也包含共有信号C0,共有信号修正方法与(4)相同。修正后的输出信号流成功概率的计算式为:


(6)迭代。
迭代的SA如图6a所示。SA由1个构件组成,某个功能是n次执行该构件来完成,即当且仅当构件C、连接件L、迁移过程正常工作时,系统才正常[6]。为迭代结构建立的 GO图及故障树如图6b和图6c所示。
由故障树求得系统故障概率计算式为:

Figure 6 Iteration software architecture,its GO chart and fault tree图6 迭代型SA及其GO图和故障树
文献[6]中迭代结构SA的可靠性等于构件与连接件可靠性乘积的n次幂,那么当n越大,则系统可靠性将越小,甚至可能趋近于0,这显然不合理。GO运算考虑的是由 GO图描述的系统结构的可靠性,由参考文献[8,9]可得闭环系统的定量计算公式为(该公式不考虑部件的维修率):PR= PS0×PC1×PL1=PC1×PL1。如果要计算系统运行时的可靠性,在处理迭代结构时也不能简单地将系统的可靠性计算为构件与连接件可靠性乘积的n次幂。

由故障树求得系统故障概率计算式为:C1、L1,2和B构件组成的顺序结构,其中B又可看成是由C2、L2,3、L2,4、C和D 组成的或分支,C是由C3、L3,5、L3,6、C5和C6构成的与分支,D是由C4、L4,7、L4,8、C7和C8构成的或汇合。

Figure 7 Software architecture diagram图7 一个软件体系结构图
3.1 基于故障树法的软件体系结构可靠性分析
故障树分析法是一种自顶向下识别系统故障的方法,它已被广泛用于软件的可靠性分析中,应用故障树法分析软件系统时,可从一个系统故障(顶事件)的失败事件着手,来找到引发故障的所有可能因素(基本事件),通过自上而下地分析因素间的因果逻辑关系,并以图形演绎方法建立软件故障树,最后根据建立的故障树进行可靠性分析。
为图7建立的故障树如图8所示。

Figure 8 Fault tree of figure 7图8 图7例子的故障树
3 实例研究
本节应用文献 [6]的实例作为研究实例,如图7所示,分别说明应用GO法和故障树法对该SA进行可靠性分析的具体过程,并对两种方法得出的结果进行对比分析。
图7所示的软件体系结构可看成是由构件
对图8所示故障树求取其最小割集为:{C1},{L1,2},{C2},{C1},{L2,3,C},{L2,3,D},{L2,4,C},{L2,4,D},{L2,3,L2,4}。
假设构件的可靠性分别为:PC1=0.97,PC2= 0.97,PC3=0.96,PC4=0.94,PC5=0.95,PC6= 0.95,PC7=0.90,PC8=0.90,连接件的可靠性分别为:PL1,2=0.97,PL2,3=0.95,PL2,4=0.92,PL3,5= 0.95,PL3,6=0.95,PL4,7=0.90,PL4,8=0.90。计算得到的系统故障率为:
PS=1—PC1×PL1,2×PC2×(1—(1—PL2,3×PC3×PL3,5×PC5×PL3,6×PC6)×(1—PL2,4×PC4×(1—(1—PC7×PL4,7)(1—PC8× PL4,8))))=0.1264
那么,系统成功概率为0.873 6。
3.2 基于GO法的软件体系结构可靠性分析
用GO图分析软件体系结可靠性的前提是构件和连接件的可靠性已知。设构件Ci成功状态概率为PCi,连接件Li的成功状态概率为PLi。
3.2.1 定量计算
基于GO法的软件体系结构可靠性分析步骤:第一步对系统软件体系结构进行分解,通过递归的方法,每次依顺序、与汇合、或汇合、与分支、或分支或迭代的形式,对系统的软件体系结构自顶向下进行逐级分解,直至分解所得的每一个部分都只含有单一的顺序、与汇合、或汇合、与分支、或分支或迭代结构为止[6]。第二步建立 GO图,根据分解后的软件体系结构建立GO图,对于分解出来的各个部分可先建立GO子图;然后用一个等效操作符代表相应的GO子图,GO子图的输出信号流的成功概率作为等效操作符的成功概率;最后建立起整个软件体系结构GO图。第三步GO运算,根据建立的GO图,进行GO运算。
下面以图7所示软件体系结构为例,说明应用GO法对该SA进行定量计算的具体过程,其步骤如下:
(1)对软件体系结构进行逐级分解,分解结果如前所述。
(2)建立GO图。通常对于分解出来的位于顶层的与分支或或分支结构可以不用建立GO子图,而是将其直接画在整体GO图中;其他情况下,对于分解出来的与分支、或分支、与汇合、或汇合及迭代结构都应绘制GO子图,因此为图7中的C、D分别建立了GO子图,如图9a和图9b所示,整个软件体系结构的GO图如图9c所示,其中编号为C'3、C'4的操作符是图9a、图9b所示GO子图的等效操作符。
(3)GO定量运算。假设的构件及连接件可靠性见3.1节。

上式中信号流C'3和C'4包含共有信号C2,因此在求信号流1的概率时需要进行修正,修正并代入后的计算式如式(3)所示,它也是SA的可靠性计算公式,它与文献[6]中给出的计算公式相同,与故障树分析结果一致。
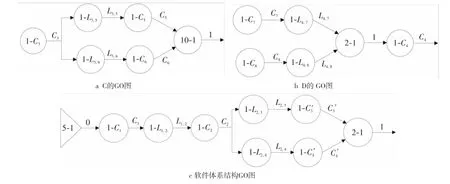
Figure 9 GO chart and sub graphs for the software architecture图9 软件体系结构GO图及其GO子图


3.2.2 定性分析
GO法的特点之一就是可以应用操作符状态概率计算式来直接定量计算系统状态概率,而不必首先进行定性分析[7]。另外,对于两状态系统,GO法可直接应用定量计算结果进行定性分析,得到系统最小割集。文献[7]中给出了直接定性分析方法。对图7采用文献[7]中给出的方法求得最小割集,如表1所示,与故障树法得到的最小割集一致。

Table 1 The minimal cut sets of the system表1 系统最小割集
最小割集中操作符故障状态的组合代表系统功能部件故障事件的组合,最小割集的发生概率可用这些部件故障概率的乘积表示。计算得到系统最小割集发生概率的总和为0.136 6,这是系统故障概率的近似值,可作为系统故障概率的上限。进行系统定性分析时,可将最小割集的发生概率作为评价其重要度的依据,对于发生概率高的最小割集中操作符代表的构件,在实际系统开发中应给予重点关注。
3.3 结果分析
相比文献[6]的方法,本方法既可以对SA的可靠性进行定量计算,又可以进行定性分析,另外还可以利用GO图直接进行定性GO分析[7]。本文提出的方法可在软件开发的各阶段对软件可靠性进行分析。在开发早期,在构件及连接件可靠度已知的情况下,可通过定量GO运算对整个软件体系结构的可靠性进行评估,而定性GO分析又可说明各构件及连接件的重要性,对后期系统的设计与开发具有一定的指导意义。在开发后期,同样可通过定量GO运算计算整个软件的可靠性,通过定性GO分析来分析系统故障原因。
当用GO图模拟比较复杂的系统结构时,可以通过分解的方法,先建立GO子图,再建立GO图,降低GO图的复杂性,从而降低分析的复杂性。另外借助Matlab工具可以实现简便的定量计算。
对图7采用故障树法进行分析时,得到的最小割集及系统成功的概率计算结果与GO法分析结果一致。GO法最大的优势就是可以直接进行定量计算,而不需要事先求出最小割集;GO法能够计算出各输出信号流的成功概率,而故障树法只能得到最终系统的故障概率;GO法是依照系统原理图或结构图来建模,对于不同的入建模型差别不会很大,方便检查核对,而故障树的建立受人为因素影响较大,不同的分析人员所建立的故障树可能会有较大的差别。
4 结束语
GO法目前多用于工程系统可靠性分析,将GO法应用于软件可靠性分析中尚处于研究阶段。本文探讨了如何将GO法应用于软件体系结构的可靠性分析中,实践证明,此方案是可行的。
当然方法也有缺陷,如,该方法被用在软件开发早期对软件进行可靠性评估时,进行定量GO运算须已知构件及连接件的可靠性数据;由软件体系结构建立GO图目前还是手工建模;在对复杂系统进行建模时,虽然可以通过分解的方式降低建模的复杂度,但仍具有一定的难度,从而造成实用性较差;此外,构件的状态迁移概率并没有在 GO图中反映出来。接下来的工作包括对GO图进行扩展,将构件的状态迁移属性添加到GO图中,使其更具有通用性;为建模过程的自动化提供方便有效的工具支持,使其更具有实用性。
[1] Feng Chong,Jiang He,Feng Jing-fang.The theory and practice of software architecture[M].Beijing:People's Posts and Telecommunications Publishing House,2004.(in Chinese)
[2] Yacoub S M,Cukic B,Ammar H H.A scenario-based reliability analysis approach for component-based software[J]. IEEE Transactions on Reliability,2004,53(4):465-480.
[3] Wang Wen-li,Pan Dai,Chen Mei-hwa.Architecture-based software reliability modeling[J].Journal of Systems and Software,2006,79(1):132-146.
[4] Mao Xiao-guang,Deng Yong-jin.A general model for component-based software reliability[J].Journal of Software,2004,15(1):27-32.(in Chinese)
[5] Gokhale S S.Architecture-based software reliability analysis:Overview and limitations[J].IEEE Transactions on Dependable and Secure Computing,2007,4(1):32-40.
[6] Zhou Na-qin,Zhang You-sheng.Reliability analysis based on software architecture[J].Computer Engineering and Applications,2008,44(30);68-71.(in Chinese)
[7] Shen Zu-pei,Huang Xiang-rui.Principle and application of GO methodology:A system reliability analysis methodology [M].Beijing:Tsinghua University Press,2004.(in Chinese)
[8] Wang Gui-li.System reliability analysis GO methodology and research[D].Harbin:Harbin Institute of Technology,2006. (in Chinese)
[9] Xu Zhi,Chen Bin-bing.Equivalent substitution idea for maintainable closed-loop system GO methodology[J].Communications Technology,2009,42(11):238-240.(in Chinese)
[10] Zhang You-sheng.Software architecture[M].2nd edition. Beijing:Tsinghua University Press,2006.(in Chinese)
附中文参考文献:
[1] 冯冲,江贺,冯静芳.软件体系结构理论与实践[M].北京:人民邮电出版社,2004.
[4] 毛晓光,邓勇进.基于构件软件的可靠性通用模型[J].软件学报,2004,15(1):27-32.
[6] 周娜琴,张友生.基于软件体系结构的可靠性分析[J].计算机工程与应用,2008,44(30):68-71.
[7] 沈祖培,黄祥瑞.GO法原理及应用:一种系统可靠性分析方法[M].北京:清华大学出版社,2004.
[8] 王桂丽.系统可靠性分析 GO法及其应用的研究[D].哈尔滨:哈尔滨工业大学,2006.
[9] 徐志,陈彬兵.可维修闭环系统GO法等效代换思路[J].通信技术,2009,42(11):238-240.
[10] 张友生.软件体系结构[M].第2版.北京:清华大学出版社,2006.

贺慧琳(1980),女,湖南衡阳人,硕士,讲 师,研 究方 向 为 系 统 可 靠 性。E-mail:hhl1998hhy@qq.com
HE Hui-lin,born in 1980,MS,lecturer,her research interest includes system reliability.
Application of the GO methodology in reliability analysis of software architecture
HE Hui-lin
(School of Mathematics&Physics,University of South China,Hengyang 421001,China)
The GO methodology is a method of system reliability analysis,which is applied in the reliability analysis of software architecture.Based on the characteristics of software architecture and the relationship among components,we build GO models with six basic structures,and conduct quantitative GO operations.We demonstrate the whole process of reliability analysis of software architecture using the GO methodology through an example.The practice indicates that the reliability of software architecture can be calculated through quantitative GO operations.The importance of components and connectors can be evaluated via qualitative GO analysis,which has a certain guiding significance for the design and development of the system.
GO methodology;reliability analysis;software architecture
TP302.7
A
10.3969/j.issn.1007-130X.2015.08.016
1007-130X(2015)08-1525-08
2014-05-23;
2014-12-02
湖南省衡阳市科技局基金资助项目(2013KJ19)
通信地址:421001湖南省衡阳市南华大学数理学院
Address:School of Mathematics&Physics,University of South China,Hengyang 421001,Hunan,P.R.China
