串联谐振注入式有源电力滤波系统稳定性分析

王少杰，王鸿健，罗安



串联谐振注入式有源电力滤波系统稳定性分析

王少杰1, 2，王鸿健1，罗安2

(1. 邵阳学院 电气工程系，湖南 邵阳，422000;2. 湖南大学 电气与信息工程学院，湖南 长沙，410082)

为了兼顾系统的滤波性能及无功补偿，又能维护系统的稳定性，提出一种新型串联谐振注入式有源电力滤波器拓扑结构并建立相应的数学模型，对其工作原理进行系统分析，探讨它在电网电压畸变、电网电压波动性以及在系统延时和惯性情况下的工作原理，并分别对电网电压畸变、电网电压波动性、系统延时及惯性这3种情况的稳定性进行系统分析研究，利用仿真软件对其结果进行仿真。研究结果表明：上述系统具有良好的稳定性和可靠性，满足了无功补偿，可以较好地应用于工业电力系统。

串联谐振；有源电力滤波；稳定性；延时；惯性

随着电力电子装置的广泛应用，电力系统的谐波污染日益严重。传统的滤波方法是采用基于谐振原理的无源滤波器，只能滤除设定次数的谐波，且易与电网产生串、并联谐振。有源滤波器(active power filter，APF)因能动态治理各次谐波而成为谐波滤除的主要发展方向[1−3]。目前的研究重点主要集中于有源滤波器的拓扑结构、控制策略、补偿特性、谐振抑制能力、谐波检测方法[4−8]和电流跟踪控制算法[9−15]，对系统稳定性问题涉及很少，为此，本文作者在新型串联谐振注入式有源电力滤波器拓扑结构上，分析在电网电压畸变、电网电压波动时、系统延时和惯性情况下的稳定性。

1 新型串联谐振注入式有源电力滤波器拓扑结构

新型串联谐振注入式混合型有源电力滤波器SRIHAPF(series resonant injection hybrid active power filter)如图1所示。图1中：S为电网阻抗；S为电网电流；F为无源支路电流；L为负载电流。假设电源谐波电压为Sh，电网系统阻抗为Sh，负载谐波电流源为Lh，而有源部分被控制为理想的谐波电压源I，则带有注入式结构的传统混合型有源电力滤波器的谐波域单相电气模型可以表示为图2，其中Sh，Fh，Lh，Ph，Ch，Rh和Gh分别为电网支路、无源支路谐波、负载支路、并联无源支路、有源支路、附加电感电路、串联谐振注入支路的电流，Sh，Ph，Gh和Rh分别为电网阻抗、无源部分阻抗、有源串联谐振支路等效阻抗、附加电抗电路阻抗。

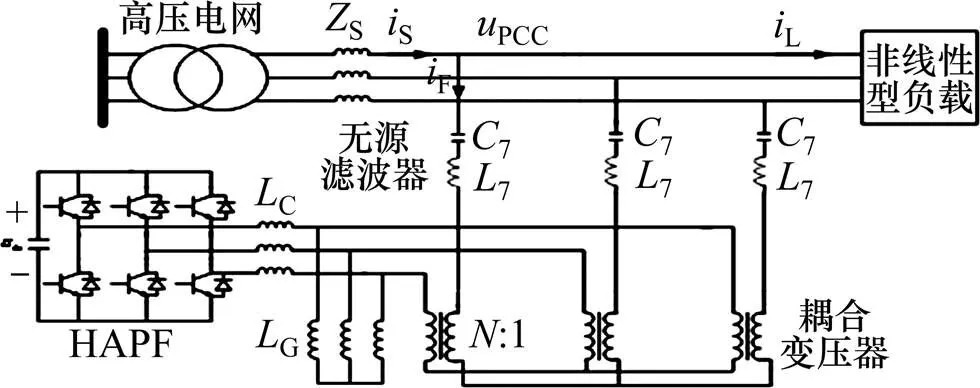
图1 串联谐振注入式混合型有源电力滤波器

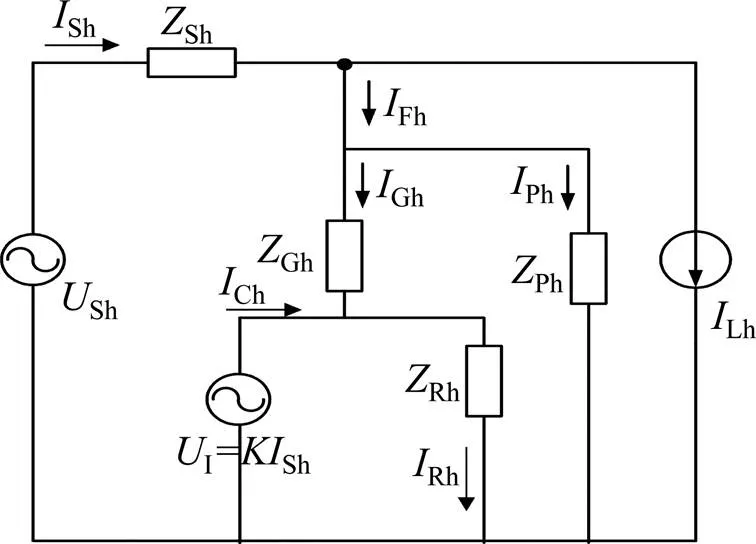
图2 SRIHAPF系统单相等效电路图

串联谐振混合有源滤波器SRIHAPF则没有基波并联支路，即Rh为一小电感阻抗，Gh为相应的由传统的注入电容的等效阻抗替换为一组单调谐滤波器的等效阻抗。图2所示为单相等效电路图。

2 电网电压畸变时SRIHAPF稳定性分析

理想条件与实际工况常常是有差别的，从严格意义上说，它们都不是理想的谐波电流源或谐波电压源。在实际工况中，将一个很大的谐波阻抗与理想的谐波电流源并联所形成的电路成为电流型谐波源。而理想的谐波电流源内阻抗为无穷大，相当于断路，见图3。非理想谐波电流源等效阻抗为Lh，无源支路电流为Ph1，谐波阻抗支路电流为Ph2。针对实际工况与理想条件的差别，下面有针对性地分析非理想谐波电流源条件下的SRIHAPF补偿的特性。

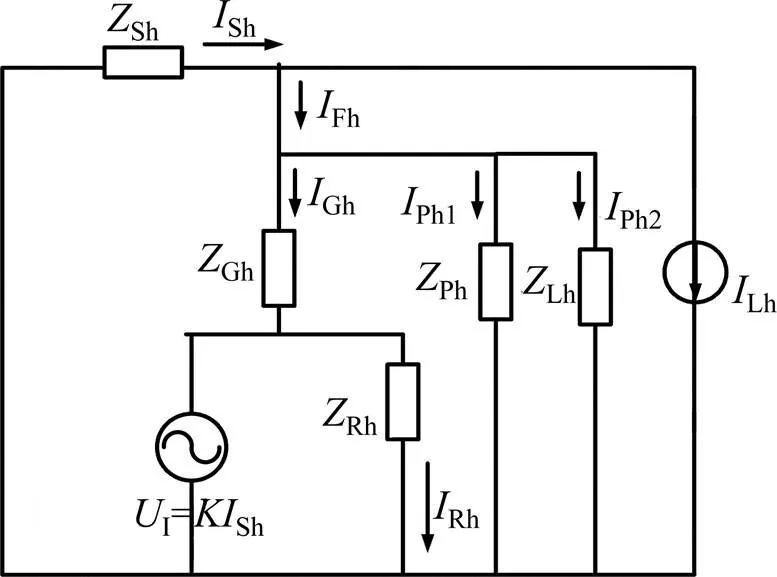
图3 SRIHAPF补偿非理想谐波电流源的单相等效电路

对于非理想的谐波电流源，电路方程为

则其谐波电流抑制函数为

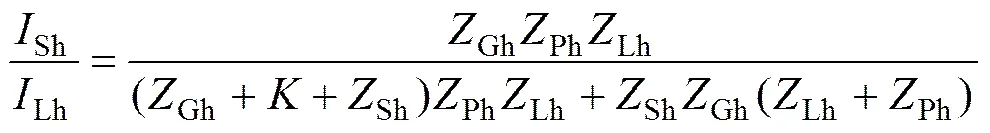
据式(2)，可以将Lh看成为1个等效阻感元件。下面分析SRIHAPF在不同的谐波源内阻抗Lh下，其补偿非理想谐波电流源的特性。

当无源滤波器投运和SRIHAPF工作时，取L= 1 Ω，可以得出不同的L谐波抑制函数频谱特性可由图4描述。取L为50，5和0.5 mH，在=0时，PPF的补偿特性如图4(a)所示；取L为50，5和0.5 mH，在=20时，SRIHAPF的补偿特性用如图4(b)所示。发现图4(b)中的3条曲线差不多重叠，由此可知：无源滤波器的补偿性能受谐波源内阻抗Lh的影响较大，SRIHAPF的补偿特性受谐波源内阻抗Lh较小。

: (a)0；(b) 20

/mH: 1—50; 2—5; 3—0.5

图4 SRIHAPF对非理想谐波电流源的补偿特性

Fig. 4 Compensation characteristics of non-ideal harmonic current of SRIHAPF

经分析可知：对于非理想谐波电流源，PPF补偿特性受谐波源内阻抗的影响不大；SRIHAPF的补偿特性几乎不受谐波源内阻抗影响。

3 电网电压波动时SRIHAPF稳定性分析

图5所示为电网电压聚升时SRIHAPF的暂态仿真波形。由图5可知，在0.6 s时SRIHAPF的有源滤波部分投入运行，假定0.8 s时电网电压由35 kV骤升到100 kV。由图5(b)和(c)可知：直流侧电压约有60 V波动，但是在0.2 s之内就恢复了稳定；a相电流、b相电流和c相电流峰值约有15 A波动，不过在0.2 s之内就恢复了稳定。

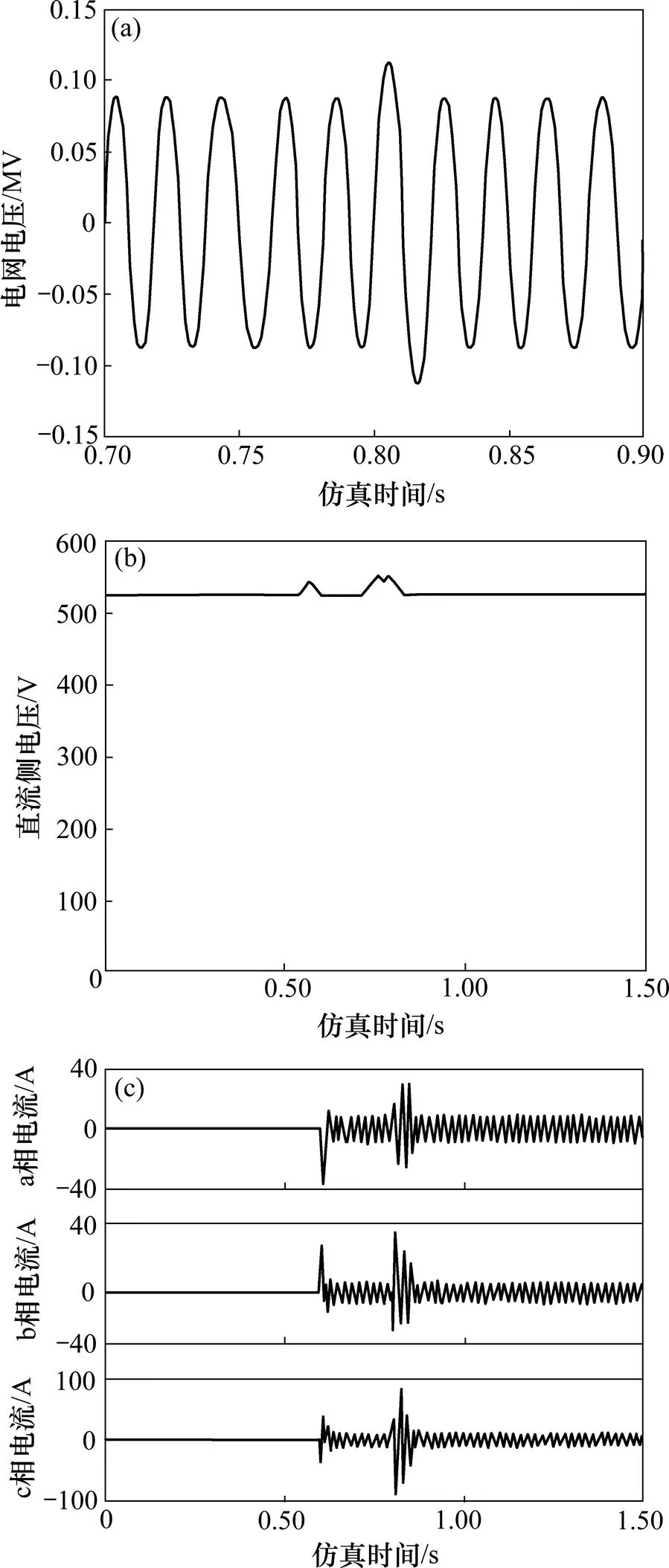
(a) 电网电压波形图；(b) 有源逆变器直流侧电压；(c) 有源逆变器三相输出电流

图5 电网电压聚升时SRIHAPF稳定性暂态仿真波形

Fig. 5 Transient simulation waveforms of SRIHAPF when grid voltage rises suddenly

电网电压骤升时，SRIHAPF稳定性暂态仿真波形如图6所示。0.6 s时有源滤波器投入运行，假定0.8 s时电网电压下陷。从图6可以看出：直流侧电压和有源逆变器3相输出电流发生突变后很快恢复至稳定值，说明系统具有很好的鲁棒性。

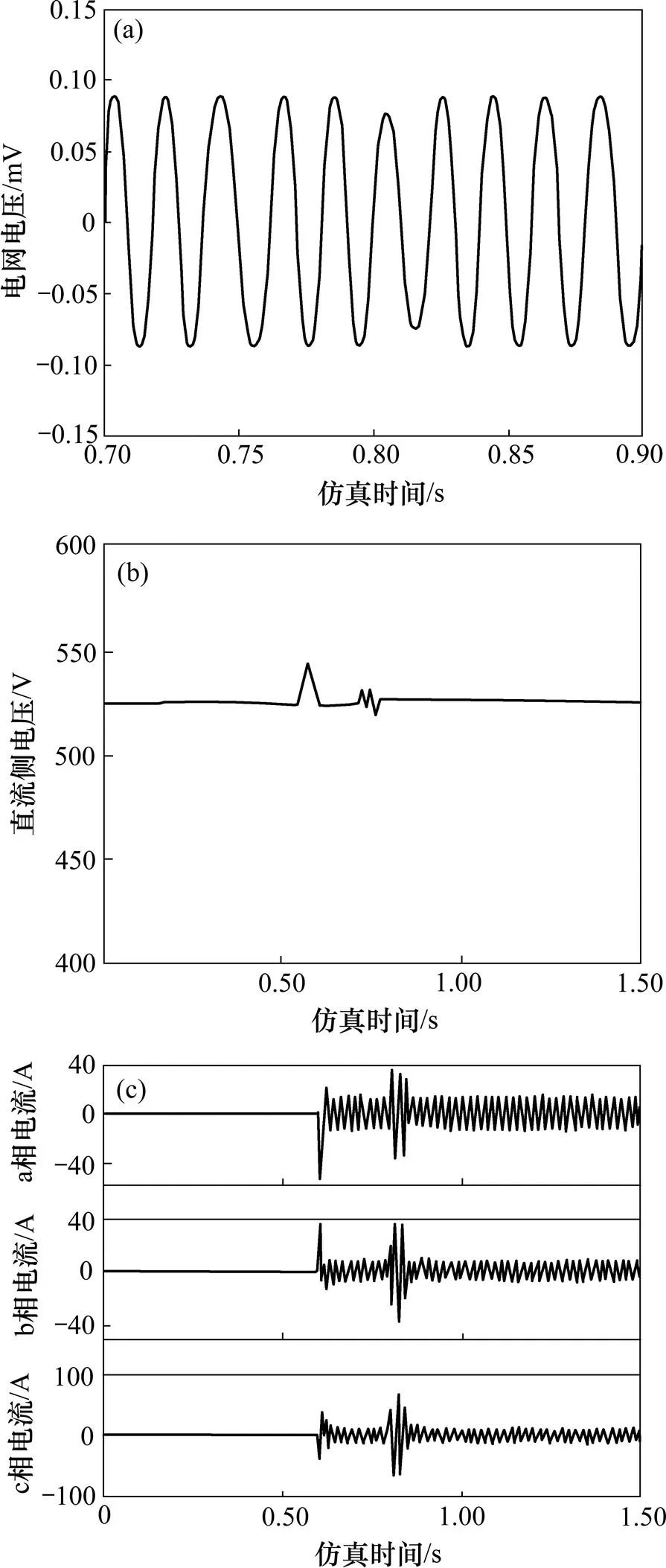
(a) 电网电压波形；(b) 有源逆变器直流侧电压；(c) 有源逆变器3相输出电流

图6 电网电压聚升时SRIHAPF稳定性暂态仿真波形

Fig. 6 Transient simulation waveforms of SRIHAPF when grid voltage rises suddenly

综上所述，该系统结构简单，能较好地处理高电压等级电网中的谐波，同时能够补偿大容量的无功功率。其最大的优点是有源部分承受的基波电压低，所需逆变器的容量小，且在系统上电瞬间、电网电压发生突变及电网发生故障时，有源部分受到的冲击很小，系统稳定性高。

4 考虑系统延时和惯性情况下SRIHAPF稳定性分析

SRIHAPF的稳定性对于整个系统的稳定运行至关重要。当把有源部分作为受控电压源时，这时仅单独考虑谐波电流源的作用，控制好I(I=×Sh，Sh为电网支路电流的谐波分量，为控制放大倍数)。串联谐振支路和无源部分就只发挥补偿的作用。只从谐波电流源的影响程度考虑，即Sh=0，并根据KCL和KVL定律，得

化简式(3)得

由式(4)得

SRIHAPF抑制负载谐波电流的系统闭环控制流程如图7所示。

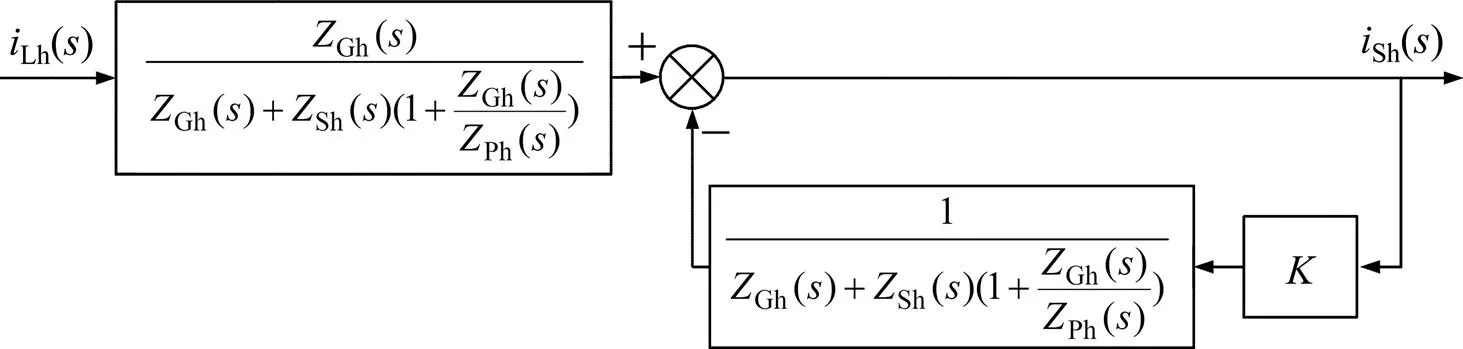
图7 SRIHAPF系统闭环控制框图

假设电网阻抗为

无源滤波器由5次和11次单调谐滤波器组成：

因此，无源部分s域的表达式为

谐波电流串联谐振在7次时的阻抗为

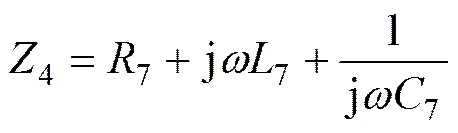
则系统的电流闭环传递函数为

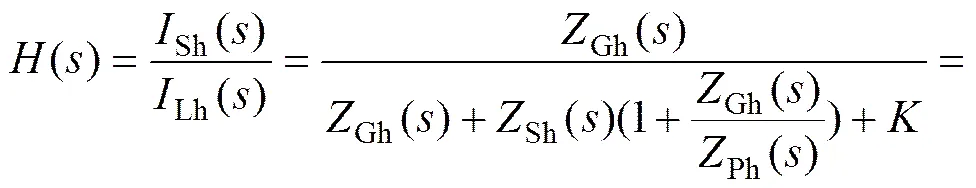
系统的特征方程为

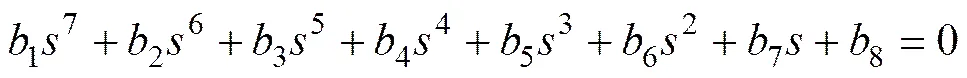
式(11)是阶次较高的方程，其根很难求出，为此，采用劳斯判据(Routh)分析系统的稳定性。在系统闭环情况下，特征方程的Routh如表1所示。

表1 闭环特征方程的Routh

表1中：

分析式(12)可知：保证系统稳定的条件就是闭环特征方程的所有系数均大于0，而分布在劳斯判据(Routh)表中第1列的所有元素都要大于0。鉴于分布在闭环特征方程中的全部系数都大于0，因此，在满足下列不等式组的前提下就可以解决问题：

在式(12)中，分别将表1中无源滤波器和电网参数代入，求解不等式组，结果发现式(13)恒成立，这说明系统的稳定性不受的影响。即使上述参数重新设置，结论还是一样。可见：尽管SRIHAPF系统闭环传递函数阶数很高，但其稳定性也很好，较大也能保证系统的稳定性。但考虑系统延时的影响，太大就会使系统不稳定。

当考虑系统延时和惯性时，设SRIHAPF离散控制系统中存在的总延时为d，用1个纯延时环节表示，SRIHAPF中的逆变环节为一阶惯性环节，有源滤波器的传递函数APF为

式中：APF为该有源滤波器的响应时间。为了分析方便，将线性近似为

由于延时d很小，随着阶数的增加，高次项值急剧减小直至可以忽略不计。在主要谐波补偿频率的低频段，系统闭环频率特性基本不受高次项影响，而在高频段可能会引起系统闭环频率特性的一定偏差，但整体来说对分析结果无大影响，此时，SRIHAPF的控制框图如图8所示。

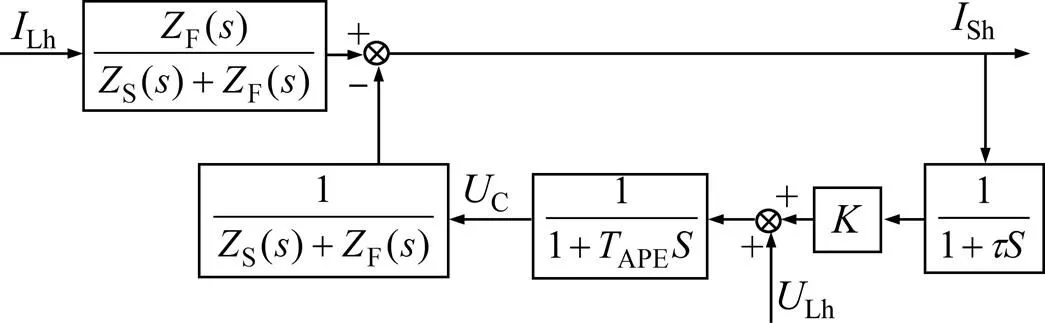
图8 考虑系统延时和惯性时系统的控制框图

设F为无源支路阻抗，则系统的闭环传递函数为

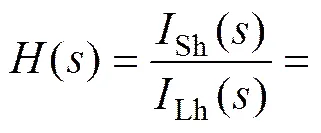
可知系统闭环根轨迹方程为

由系统固有延时和数据采集处理构成的总延时d会对系统的稳定性产生一定的影响，越大，电网谐波电流的抑制效果越好，但相应的闭环控制系统存在系统延时和惯性，这对系统的开环增益也提出了要求，过大的开环增益将直接导致系统不稳定。下面分析和系统稳定性之间的关系。

延时变化时系统闭环根轨迹见图9。从图9的根轨迹中可以看出根的取值范围；将根的取值代入式 (16)可得出相应的，不同根对应的见表2。从图9可知：当最大值为563时所对应的系统总延时d=20 μs，这时平面的右半平面不会出现系统的闭环极点；当d=50 μs时，可取最大值452，一旦取＞452，便有1对闭环极点越过虚轴，进入平面的右半平面；当d=100 μs时，使系统全部闭环极点位于平面左半平面的的最大值为325。闭环极点在系统不同延时下，不出现平面右半平面的最大取值见表2。从表2可知：受系统延时的影响，要维护系统稳定，在延时较大的情况下，只能取最大值中的较小值。

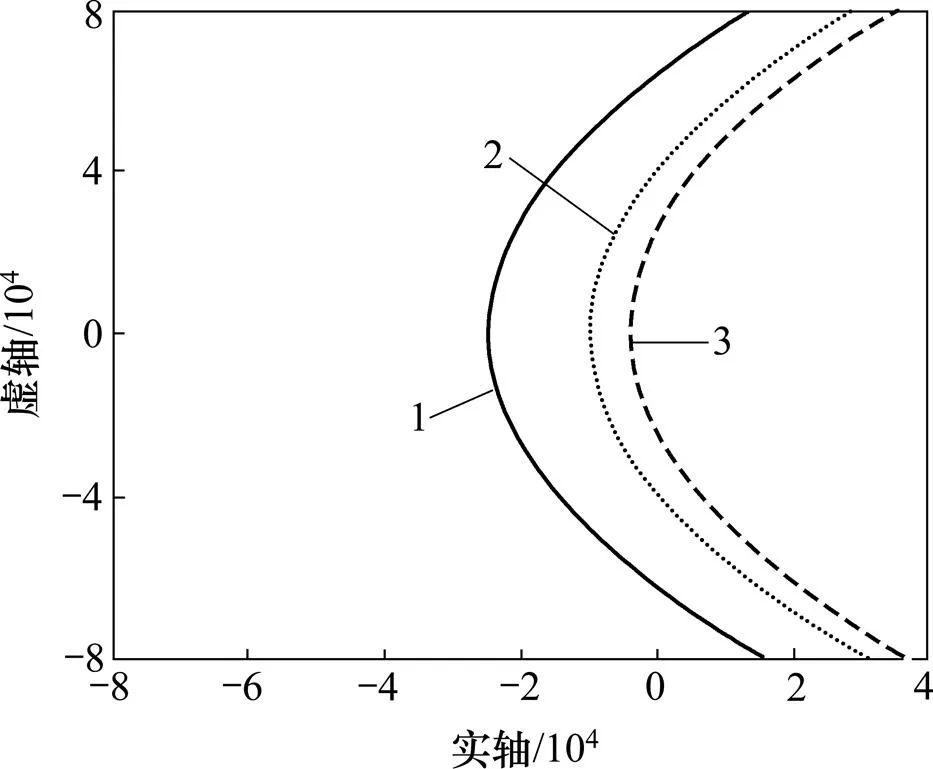
d/μs: 1—100; 2—50; 3—20

图9 延时变化时系统闭环根轨迹图

Fig. 9 Root locus of delay time in closed loop system

表2 不同延时系统稳定的K最大值Kmax

经分析可知：在同一延时条件下，随着增大，系统的稳定裕量变小并有2对闭环极点慢慢向虚轴逼近；当大于一定值时，系统进入不稳定状态，并且1对闭环极点跨越虚轴进入平面的右半平面；当更大时，该对闭环极点朝右远离虚轴，使得系统的稳定性较前更差。因此，要使系统的稳定性良好，不能太大。

5 结论

1) 提出了一种新型的串联谐振注入式混合有源滤波器的拓扑结构，并建构了相应的数学模型。

2) 在电压畸变时，SRIHAPF具有较好的补偿特性，它几乎不受谐波源内阻抗的影响，具有较好的稳定性。

3) 当电网电压波动时，SRIHAPF能够补偿大容量的无功功率，能较好地处理高电压等级电网中的谐波，还使有源部分承受较低的基波电压，所需逆变器的容量小，具有较好的鲁棒性，系统稳定性较高。

4) 当max趋近某一定值时，谐波抑制效果较好。

[1] 王兆安, 杨君, 刘进军. 谐波抑制与无功功率补偿[M]. 北京: 机械工业出版社, 1998: 1−30.
WANG Zhaoan, YANG Jun, LIU Jinjun. Harmonic suppression and reactive power compensation[M]. Beijing: Mechanical Industry Press, 1998: 1−30.

[2] 罗安. 电网谐波治理和无功补偿技术及装备[M]. 北京: 中国电力出版社, 2006: 5−25.
LUO An. The technology and equipment of harmonic elimination and reactive power compensation[M]. Beijing: China Electric Power Press, 2006: 5−25.

[3] 周臻, 夏向阳, 唐伟, 等. 基于非线性控制APF在HVDC中的谐波抑制研究[J]. 中南大学学报(自然科学版), 2013, 44(9): 3746−3751.
ZHOU Zhen, XIA Xiangyang, TANG Wei, et al. Application of active power filter on AC side of HVDC based on nonlinear control[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3746−3751.

[4] 胡志坤, 胡锰洋, 桂卫华, 等. 基于−变换的改进i−i基波正序有功和无功电流检测算法[J]. 中南大学学报(自然科学版), 2010, 41(3): 1015−1021.
HU Zhikun,HU Mengyang,GUI Weihua,et al.An improvedi-idetection approach of positive fundamental active and reactive current based ontransformation[J].Journal of Central South University (Science and Technology),2010，41(3):1015−1021.

[5] 陈海荣, 徐政. 采用空间矢量检测谐波电流的有源电力滤波器仿真研究[J]. 电网技术, 2005, 29(11): 60−64, 72.
CHEN Hairong, XU Zheng. Simulation study of active power filter detecting harmonic currents by space vector[J]. Power System Technology, 2005, 29(11): 60−64, 72.

[6] 范瑞祥, 罗安, 周柯, 等. 并联混合型有源电力滤波器的建模和控制策略分析[J]. 中国电机工程学报, 2006, 26(12): 55−61.
FAN Ruixiang, LUO An, ZHOU Ke, et al. The modeling and the control strategy analysis of shunt hybrid active power filter[J]. Proceedings of the CSEE, 2006, 26(12): 55−61.

[7] 付青, 罗安, 王丽娜. 基于自适应智能控制的混合有源电力滤波器复合控制[J]. 中国电机工程报, 2005, 25(14): 46−51.
FU Qing, LUO An, WANG Lina. A novel hybrid control based on the adaptive intelligent theorems for the shunt hybrid active power filter[J]. Proceedings of the CSEE, 2005, 25(14): 46−51.

[8] 漆铭钧, 罗安, 刘定国. 注入式有源滤波器工程应用的关键技术[J]. 电工技术学报, 2009, 25(3): 77−82.
QI Mingjun, LUO An, LIU Dingguo. The key technology in engineering application of injection type active power filter[J]. Journal of Electrician Technique, 2009, 25(3): 77−82.

[9] 王少杰, 罗安, 孙贤大. 谐波及无功电流检测低通滤波器的优化设计方法[J]. 中南大学学报(自然科学版), 2010, 41(3): 1022−1027.
WANG Shaojie, LUO An, SUN Xianda. An optimal design of low-pass filter in detection harmonic and reactive currents[J]. Journal of Central South University (Science and Technology), 2010, 41(3): 1022−1027.

[10] Corasaniti V F, Barbieri M B, Amera P L, et al. Hybrid active filterfor reactive and harmonics compensation in a distribution network[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 670−677.

[11] ZHAO Hengbing, Wu J, Kawamura A. An Accurate Approach of nonlinearity compensation for VSI inverter output voltage[J]. IEEE Trans on Power Electronics, 2004, 19(4): 1029−1035.

[12] Ryu H S, Lim I H, Lee J H, et al. A dead time compensation method in voltage-fed PWM inverter[J]. IEEE Trans on Power Electronics, 2006, 14(8): 911−916.

[13] 范瑞祥, 罗安, 李欣然. 并联混合型有源电力滤波器的系统参数设计及应用研究[J]. 中国电机工程学报, 2006, 26(2): 106−111.
FAN Ruixiang, LUO An, Li Xinran. Parameter design and application of shunt hybrid active power filter[J]. Proceedings of the CSEE, 2006, 26(2): 106−111.

[14] 童立青. 串联混合有源电力滤波器新型控制技术研究[J]. 浙江大学学报, 2009, 14(2): 38−45.
TONG Liqin. The new control technique of the series hybrid active power filter[J]. Journal of Zhejiang University, 2009, 14(2): 38−45.

[15] 周柯, 罗安, 楚红波. 新型大功率并联混合注入式有源滤波器的研究与应用[J]. 电工电能新技术, 2008, 24(1): 44−47.
ZHOU Ke, LUO An, CHU Hongbo. A new high power shunt hybri injection type active power filter research and application[J]. Advanced Technology of Electrical Engineering and Energy, 2008, 24(1): 44−47.

Stability of series resonance injection hybrid active power filter

WANG Shaojie1, 2, WANG Hongjian1, LUO An2

(1. Department of Electrical and Information Engineering, Shaoyang University, Shaoyang 422000, China;2. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)

To ensure the filtering performance of the system and the reactive power compensation, and to maintain the stability of the system, a new type of series resonant injection active power filter topology was put forward by establishing the mathematical model and analyzing the working principle of the system, the power grid voltage distortion, voltage fluctuation, system delay and inertia principle were analyzed, the stability of the above three conditions was studied, and the results were simulated using the simulation software. The results show that the system has good stability and reliability, satisfying the reactive power compensation, and it can be used in industrial power system.

series resonant; active power filter; stability; delay; inertia

TM864

A

1672−7207(2015)01−0120−07

2014−02−10；

2014−04−22

湖南省教育厅重点科研项目(13A089)；湖南省教育厅优秀青年科研项目(12B116) (Project(13A089) supported by the Key Scientific Research, Education Department of Hunan Province; Project(12B116) supported by Outstanding Youth Project of Education Department of Hunan Province)

王少杰，男，博士，副教授，从事高电能质量输配电技术研究；E-mail: shaojiew@163.com

10.11817/j.issn.1672−7207.2015.01.017

(编辑 陈灿华)