直升机分扭传动直齿轮疲劳寿命评估方法

丁晟，刘少军，胡贇



直升机分扭传动直齿轮疲劳寿命评估方法

丁晟，刘少军，胡贇

(中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083)

为得到直升机主减速器分扭传动系统中关于直齿轮的疲劳寿命评估方法，在Lundberg−Palmgren疲劳寿命理论(L−P理论)和Hertz接触理论的基础上建立主动轮单齿疲劳寿命评估模型。该模型所需参数主要与轮齿啮合时的最大Hertz接触应力相关。为利用有限元分析软件ANSYS求解此应力，确定主动轮单齿在啮合区的各啮合界点，并推导啮合区上的载荷分布规律，得到基于载荷谱多工况作用下主动轮的疲劳寿命评估方法，并针对某直升机在单工况作用下的直齿轮给出疲劳寿命评估算例。研究结果表明，该方法所得疲劳寿命估算值比试验值更加保守，是一种安全、有效的疲劳寿命估算方法。

直齿轮；疲劳寿命；Lundberg−Palmgren理论(L−P理论)；Hertz接触理论；载荷分布

疲劳寿命分析是直升机研究的重要内容，同时也是传动系统可靠性校核的关键技术指标。该指标要求直升机的零部件具有设计要求的疲劳寿命，而且需以要求的置信度保证直升机在使用期内发生疲劳损坏的概率极小。从20世纪40年代起，尤其是近30年来，各国围绕直升机的疲劳寿命评估开展了大量研究，如美国在ART(advanced rotorcraft transmission)，RDS-21 (rotorcraft drive system for the 21 century)计划以及NASA公布的相关文件中，都将传动系统的寿命列为关键技术[1−3]。然而，这些研究往往更多地关注传动系统中结构件的疲劳寿命，对于传动系统中关键、重要部件的疲劳寿命研究较少，国内在这方面的研究更是欠缺。事实上，以高周振动疲劳为主的直升机传动系统关键、重要部件的特点是载荷复杂、结构特殊、飞行状态复杂多变，加之其多为单通道传力的构件，一旦在飞行中发生疲劳破坏往往导致灾难性事故，因而，有必要对直升机传动系统中关键、重要部件的疲劳寿命进行评估[4]。本文以直升机分扭传动系统中的直齿轮作为研究对象，考虑到其所处工况的多变性以及外加载荷的复杂性，其疲劳失效的机理与疲劳寿命的计算方法都与一般齿轮的不同，因而本文拟在基于Lundberg− Palmgren疲劳寿命理论和Hertz接触理论的基础上，建立直齿轮疲劳寿命评估模型，形成可靠的疲劳寿命评估方法。

1 分扭传动结构

直升机主减速器中齿轮传动系统[5]如图1所示。整个齿轮传动系统分为3级：第1级齿轮传动为斜面齿轮传动，通过斜面齿轮30与斜面齿轮34的啮合传动将转速方向从向变为向；第2级齿轮传动为分扭构型传动，通过直齿轮38与直齿轮42A和42D以及直齿轮40与直齿轮44B和44C的啮合传动将功率分为4条路径传输，避免了扭矩过大导致直齿轮过快疲劳失效问题；第3级齿轮传动为人字齿轮传动，通过人字齿轮48A，48B，48C和48D与人字齿轮32的啮合传动将功率合一并输出。

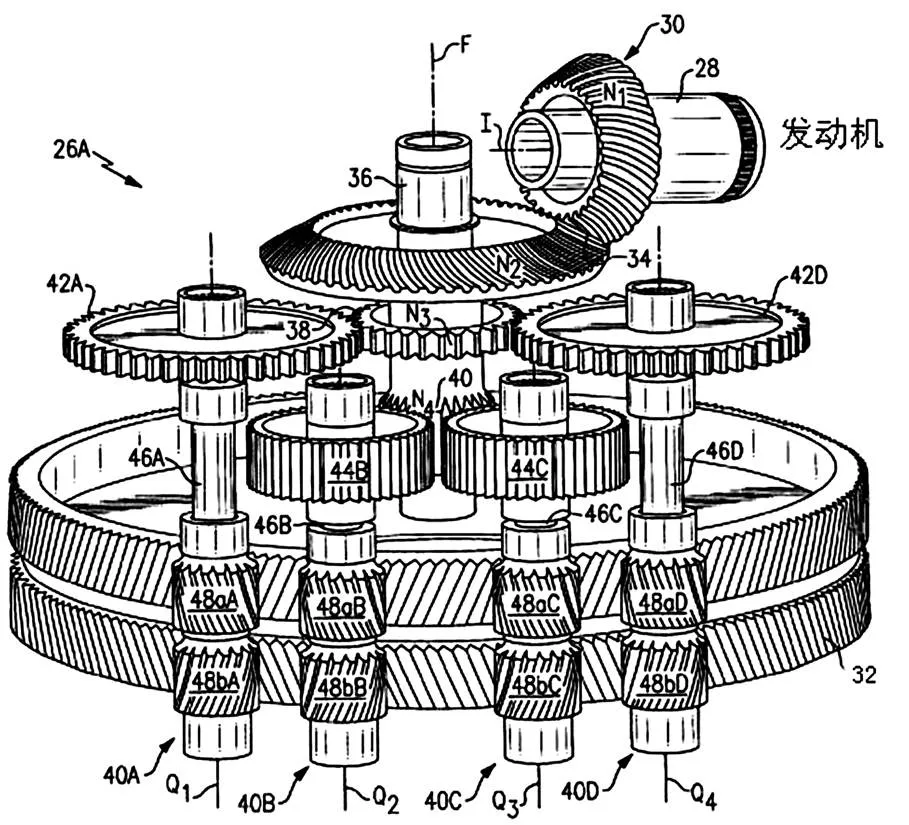
图1 单分扭齿轮箱模块示意图

2 疲劳寿命评估方法

2.1 疲劳寿命评估理论

2.1.1 Lundberg−Palmgren疲劳寿命理论

Lundberg等针对轴承的疲劳寿命建立了数学分析模型[6]。该模型假定轴承疲劳失效源于接触下表面由高应力影响下轴承材料中应力分布的不协调所引起的疲劳点蚀，对于生存概率、应力影响因子和寿命三者之间有如下关系式：

式中：为生存概率；为高应力影响区域的体积；为应力循环次数即寿命；G为Weibull斜率；和为材料指数；0为临界应力深度；为临界应力。

在此数学模型基础上，文献[6]认为，基于疲劳失效原理的相似性，此模型同样适用于对齿轮疲劳寿命的评估。因此，当生存概率通常作为设计指标既定时，式(1)左边变为常量，则应力循环次数可以视为只与高应力影响区域体积、临界应力深度0和临界应力相关的变量。式(1)变换后的比例关系式如下：

对于航空用AISI 9310钢直齿轮，其Weibull斜率G以及材料指数和已由NASA给出通用值[7]，故下面着重探讨高应力影响区域体积、临界应力深度0和临界应力的转化求解。

2.1.2 Hertz接触理论

忽略齿轮啮合时的相对滑动及摩擦，其啮合时的接触可以近似看成Hertz线接触[8]。对于材料相同的1对齿轮，其啮合时接触椭圆的长、短半轴、表达式[9]如下：

式中：为齿宽；为外加载；0为与弹性模量有关的系数；为综合曲率半径。0和表达式如下：

式中：为弹性模量；1/为泊松比；和分别为主动轮和从动轮曲率半径，

1为主动轮分度圆半径；为主动轮压力角；1和2分别为主动轮和从动轮齿数。

对于航空用齿轮，其疲劳失效通常是由最大反向正交剪应力引起，此最大反向正交剪应力作用在距接触表面下距离为0处，振幅在之间变动。在Hertz线接触理论中，应力深度与接触椭圆短半轴之间，振幅与最大Hertz接触应力max之间，外加负载与最大Hertz接触应力max之间有如下关系式：

式中：1为“单齿”啮合区渐开线弧长。

由式(3)，(6)和(7)可知：忽略轮齿固有属性参数，高应力影响区域体积、临界应力深度0和临界应力这3个着重探讨的参数主要与最大Hertz接触应力相关。

此外，由于齿面接触应力为脉动循环，需将最大Hertz接触应力通过Goodman公式转化为对称循环的当量应力，其转换公式如下[11]：

2.2 单齿在1个啮合周期内的载荷分布

疲劳寿命评估主要与最大Hertz接触应力max相关，本文拟通过有限元分析软件ANSYS来实现其求解。在求解之前，需要确定轮齿在啮合周期内的载荷分布。

2.2.1 单齿啮合内界点和外界点的确定

AGMA 913-A98[12]给出了齿轮啮合时内界点和外界点的确定方法，如图2所示。图2中：点为齿廓啮合起始点；点为齿廓啮合终止点；点和点为单对齿啮合的内界点和外界点。

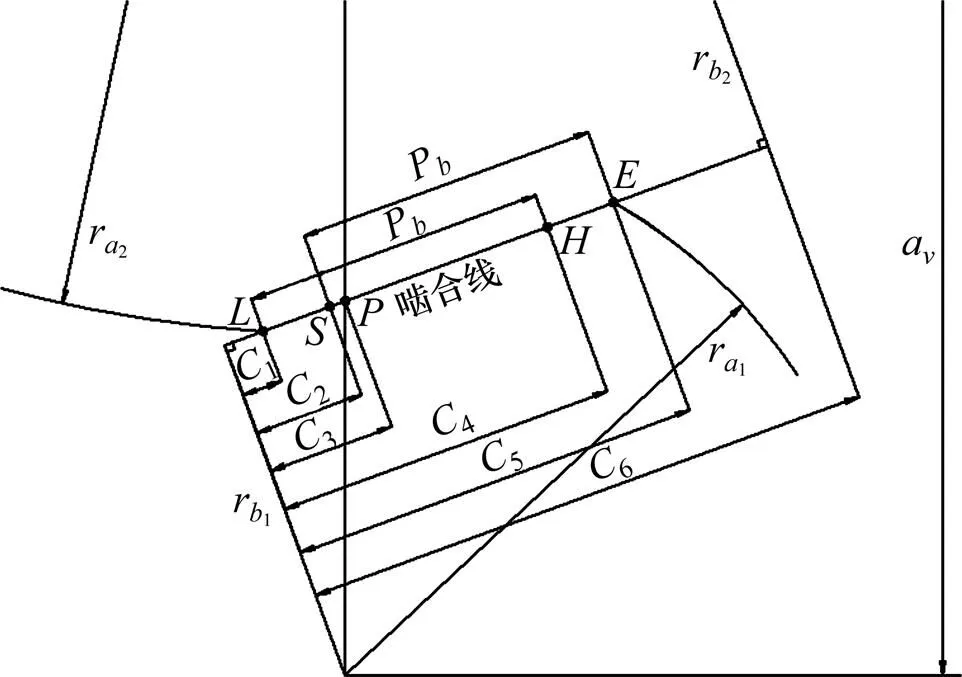
图2 啮合界点的确定

据此可知，在直角坐标系内，各啮合界点到坐标原点的距离为

式中：r为齿轮基圆半径；r为齿轮齿顶圆半径；a为中心距；p为齿轮基节。

2.2.1 啮合区上任一点法向力

对于齿轮单齿，沿实际啮合区域载荷分布近似服从如下规律[13]：

式中：L和L为载荷分配系数，参考美国航空发动机减速器齿轮强度计算方法中的参数，选用，[13]；为啮合起始点距齿顶弧长；为啮合内界点距齿顶的弧长；为啮合外界点距齿顶的弧长；为啮合终止点距齿顶的弧长；为该点距齿顶弧长；0为加载于齿顶时的法向力，

式中：为功率；为转速。

2.2.2 啮合区上任一点加载角

在直角坐标系中，沿渐开线上加载力与加载角如图3所示。

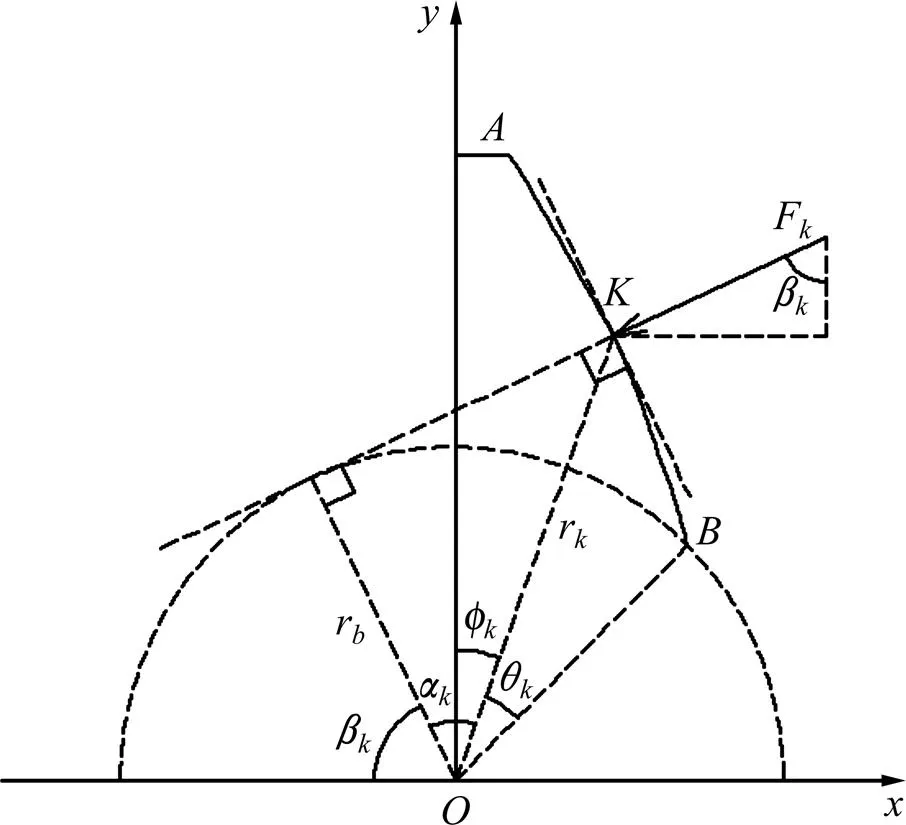
图3 渐开线上加载力与加载角简图

则啮合线上任一点的加载角为

2.3 疲劳寿命评估模型

2.3.1 主动轮单齿疲劳寿命评估模型

考虑到当设计指标生存概率为90%时，应力循环次数即为主动轮1个单齿的疲劳寿命10，联立式(2)，(3)，(4)和(6)，并略去常量比值，由式(2)得到如下比例关系式：

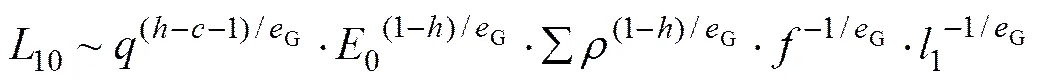
引入材料系数G，式(15)变成

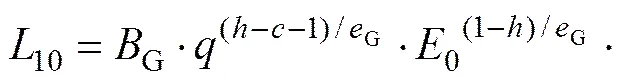
当生存概率=90%时，据式(16)可得主动轮单齿的疲劳寿命10。

2.3.2 主动轮疲劳寿命评估模型

由式(1)可知有如下比例关系式：

由式(17)可知：对于同一研究对象，以90%生存概率下的疲劳寿命10作为基准。生存概率有如下关系式：

根据独立事件的基本概率理论，对于齿数为1的分扭传动主动轮，其同时带动2对从动轮，主动轮生存概率S与主动轮单齿生存概率的关系式如下：

对于主动轮，当主动轮生存概率S为90%时，将式(19)代入式(18)有

当生存概率S为90%时，由式(20)可得主动轮的疲劳寿命L。

2.3.3 多工况下主动轮疲劳寿命评估模型

直升机在实际飞行过程中具有不同的飞行状态，各状态对应的工况可以由载荷谱得到。齿轮所处工作环境复杂而多变，其在各工况综合作用下的疲劳寿命如下：

3 疲劳寿命评估实例

3.1 主动轮基本参数与所处工况

所研究直齿轮副基本参数及材料性能分别如表1和表2所示。

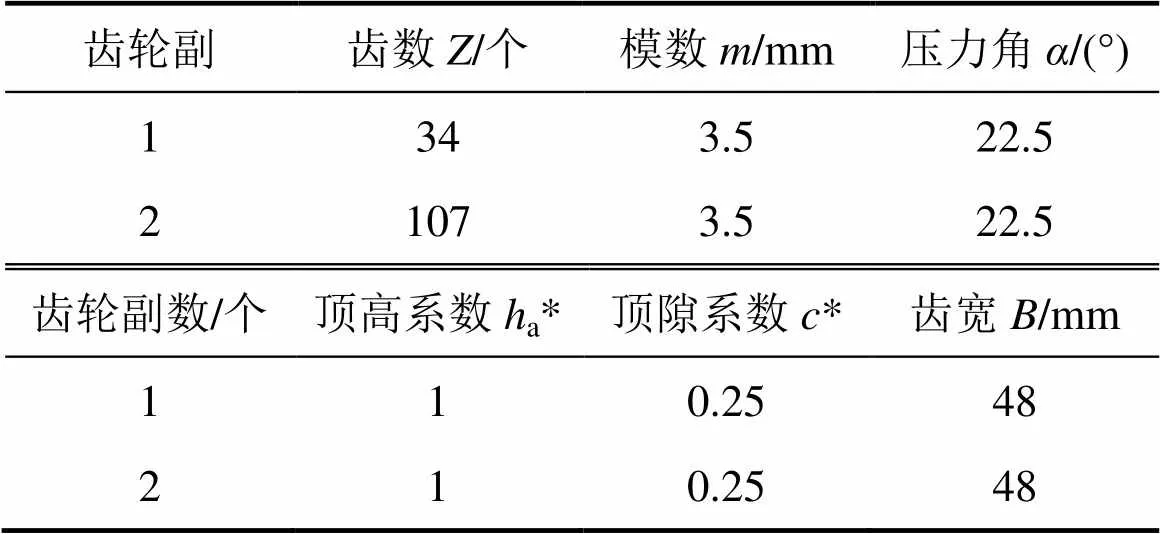
表1 齿轮副基本参数

表2 材料性能

直升机飞行谱中含多种工况，分别对应于正常飞行时不同的飞行状态。本文为了方便说明和简化计算，只选取其中某一飞行状态进行研究，即以远航速度平飞侧滑15°，质量为“中2”时作为研究对象所处工况，其结果如表3所示。

表3 传动系统部分载荷谱

3.2 ANSYS求解最大Hertz接触应力

一个完整的平面单齿轮廓通常由齿顶曲线、工作齿廓、过渡曲线和齿底曲线这4部分组成。在这4部分曲线中，工作齿廓是轮齿啮合区域，过渡曲线虽不参与齿轮的啮合运动，但其对齿轮的应力和变形影响较显著，故有必要精确地作出工作齿廓和过渡曲线的实际齿廓。本文在ANSYS中采用APDL参数化语言对主动轮单齿进行建模。

为了求解主动轮单齿在1个啮合周期内的最大Hertz接触应力，在ANSYS中采用SOLID185作为单元类型，它为八节点低阶六面体单元，对单齿模型生成四节点的四边形映射网格，并最终经体扫略生成三维实体网格。

完成网格划分后，需对模型进行位移约束和施加载荷。假定主动轮轮齿不动，通过外加负载沿啮合区移动即移动载荷的方式来模拟齿轮副在1个啮合周期内的实际接触情况，对轮齿两侧面及底面施加全位移约束。

主动轮在啮合过程中同时带动2对从动轮，对于一侧啮合单齿而言，另一侧外加负载对其最大Hertz接触应力的影响可忽略不计。故为了求解方便，只考虑一侧外加负载。

在ANSYS求解过程中，将单齿二维端面上的实际啮合渐开线均分为21等分，则在此端面上载荷作用关键点为22个点，由此衍生到三维体中接触线为22条。每条接触线上节点个数及其坐标已知，则依据式(11)和(14)可分别得到其法向作用力和加载角。采用DO循环分别加载共22次，最终得到沿渐开线Hertz接触应力分布如图4所示。

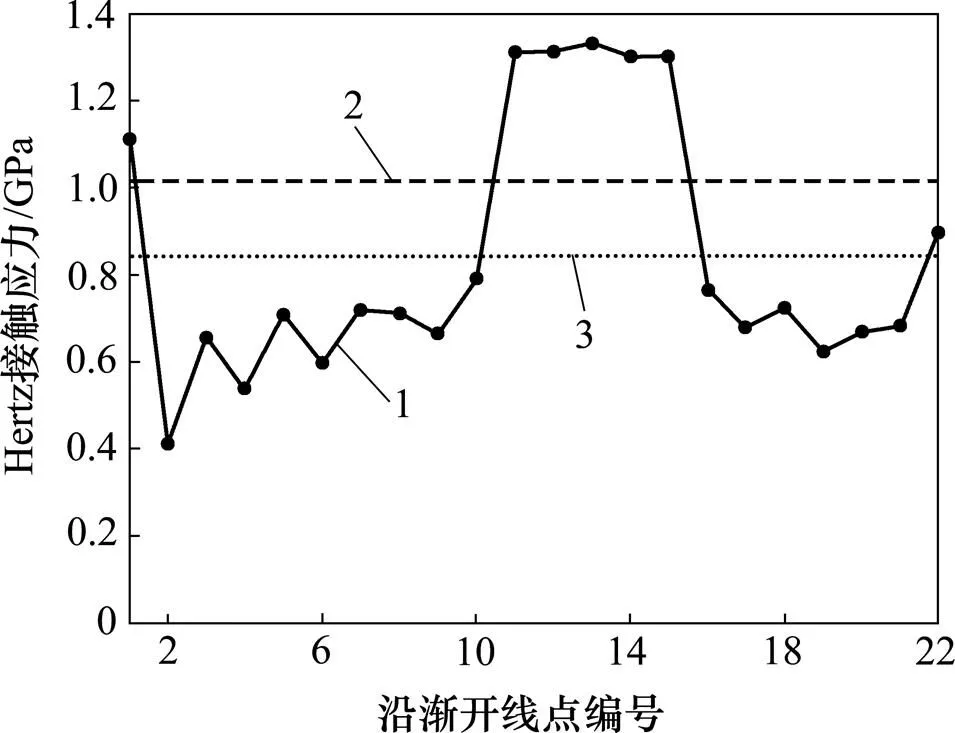
1—沿渐开线Hertz接触应力；2—修正最大Hertz接触应力；3—平均Hertz接触应力

图4 沿渐开线Hertz接触应力

Fig. 4 Hertz contact stress along involute line

其中，第13步为1个啮合周期内最大Hertz接触应力出现时的载荷步，其应力云图如图5所示。由此可知最大Hertz接触应力为1.331 GPa，代入式(8)得到Goodman修正当量应力为1.011 GPa。

图5 最大Hertz接触应力所处载荷步Von Mises应力云图

3.3 主动轮单工况下疲劳寿命评估

在直升机处于以远航速度平飞侧滑15°、质量为“中2”的飞行工况时，对于主动轮而言，其功率为487.5 kW，转速为7 626 r/min，在此工况下产生的Goodman修正当量应力为1.011 GPa。Lewis实验室[6]给出航空用AISI 9310渐开线直齿轮的材料影响系数为B=4.08×108，=31/3，=7/3，e=3/2。在ANSYS后台数据中可以查得最大Hertz接触应力作用点在和方向的坐标分别为2.58 mm和59.90 mm，“单齿”啮合区渐开线弧长为1.513 mm。

将上述参数代入式(16)计算得到主动轮单齿疲劳寿命10为1.978 3×106次，将其代入式(20)计算得到主动轮在该工况下疲劳寿命L为1.187 5×105次。中航某所AISI 9310直齿轮在某型齿轮疲劳试验机上于该工况下疲劳寿命的实验结果为1.620 0×105次。与之相比相对误差为26.7%，考虑到润滑对疲劳寿命的影响，且加上评估值比试验值更加保守，可以认为该疲劳寿命评估方法是有效且精确的。

4 结论

1) 在L−P疲劳寿命理论和Hertz接触理论的基础上，建立了直升机主减速器中分扭传动主动轮的疲劳寿命评估模型，得到其疲劳寿命的评估方法。

2) 利用所得到的针对直齿轮的疲劳寿命评估方法，对直升机传动系统载荷谱中某一工况下的主减速器直齿轮中的主动轮疲劳寿命进行评估，并与试验结果进行对比，研究结果表明，该方法是一种安全，有效的疲劳寿命估算方法。

[1] Pulikollu R V, McDaniels R, Krishnan G．Model based fatigue life prediction for AA 7075-T651[R]．Huntsville: American Helicopter Society International Condition based Maintenance Specialists Meeting, 2009: 328−337.

[2] Giglio M, Manes A, Fossati M. Fatigue life analysis of Al8090 helicopter fuselage panels[J]. Key Engineering Materials, 2007, 348(1): 637−640.

[3] Braddock C E, Battles R A. Design of an advanced 500-hp helicopter transmission[R]. Washington: NASA, 1983.

[4] 王海波. 直升机传动系统初始寿命确定[D]. 哈尔滨: 哈尔滨工程大学能源与动力工程学院, 2006: 10−16.
WANG Haibo. The primary life of the helicopter transmission system confirmed[D]. Harbin: Harbin Engineering University. School of Energy and Power Engineering, 2006: 10−16.

[5] Gmirya Y. Multi-path rotary wing aircraft gearbox: US,7918146B2[P]. 2009−11−12.

[6] Zaretsky E V, Lewicki D G, Savage M, et al. Determination of turboprop reduction gearbox system fatigue life and reliability[J]. Tribology & Lubrication Technology, 2008, 64(1): 40−50.

[7] Vlcek B L, Hendricks R C, Zaretsky E V. Probabilistic analysis for comparing fatigue data based on Johnson-Weibull parameters[J]. ASME International Design Engineering Technical Conferences, 2008(4): 457−469.

[8] Pedrero J I, Pleguezuelos M, Munoz M. Critical stress and load conditions for pitting calculations of involute spur and helical gear teeth[J]. Mechanism and Machine Theory, 2011, 46(4): 425−437.

[9] Genzalez P I, Iserte J L, Fuentes A. Implementation of Hertz theory and validation of a finite element model for stress analysis of gear drives with localized bearing contact[J]. Mechanism and Machine Theory, 2011, 46(6): 765−783.

[10] 周长江, 唐进元, 吴运新. 基于精确模型的齿根应力和轮齿变形载荷历程分析[J]. 机械设计与研究, 2004, 20(3): 67−70.
ZHOU Changjiang, TANG Jinyuan, WU Yunxin. Load-hist evaluation of stresses and deflection of spur gear teeth based on exact model[J]. Machine Design and Research, 2004, 20(3): 67−70.

[11] 薛向珍, 李育锡, 王三民. 某直升机主减速器传动系统的寿命与可靠性计算方法[J]. 航空动力学报, 2011, 26(3): 635−641.
XUE Xiangzhen, LI Yuxi, WANG Sanmin. Method of life time and reliability of some helicopter’s main reducer[J]. Journal of Aerospace Power, 2011, 26(3): 635−641.

[12] 成大先. 机械设计手册(第3卷)[M]. 北京: 化学工业出版社, 2008: 14-12−14-20.
CHENG Daxian. Handbook of mechanical design(Vol 3)[M]. Beijing: Chemical Industry Press, 2008: 14-12−14-20.

[13] 鲍洪, 安琦. 渐开线直齿轮轮齿载荷及应力计算方法[J]. 华东理工大学学报, 2012, 38(1): 116−122.
BAO Hong, AN Qi. A method of calculating load and stress of involute spur gear[J]. Journal of East China University of Science and Technology, 2012, 38(1): 116−122.

Evaluation method of fatigue life for split torque transmission spur gears in helicopter

DING Sheng, LIU Shaojun, HU Yun

(State Key Laboratory for High Performance Complex Manufacturing, School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

To obtain the fatigue life evaluation method for split torque transmission spur gears in helicopter’s main reducer, an mathematical model of single pinion tooth based on Lundberg−Palmgren fatigue life theory (L−P theory) and Hertz contact theory was established. The parameters of this model were mostly related to the maximum Hertz contact stress. To solve the stress by the software of ANSYS, the boundary points and the regularities of loading distributions on the meshing area were determined, including the force and angle of loading at any point in this area. According to the data above, the fatigue life evaluation method for pinion under varieties of working conditions based on loading spectrum was finally obtained, and an example which proves the method reasonable of pinion under one working condition was given. The results show that the evaluation result calculated by this method is securer than the test result, which indicate that the method is a safe and effective evaluation method of fatigue life.

spur gears; fatigue life; L−P theory; Hertz contact theory; loading distribution

TH132.4；V215.5

A

1672−7207(2015)01−0135−06

2014−02−10；

2014−04−22

国防预研项目(81302XXXX) (Project(81302XXXX) supported by the National Defense Beforehand Research Project)

刘少军，教授，博士生导师，从事深海矿产资源勘探与开采技术及直升机疲劳寿命与可靠性分析方法研究；E-mail: liumen503@gmail.com

10.11817/j.issn.1672−7207.2015.01.019

(编辑 陈灿华)