风电场风机测量风速缺损值的组合填充模型
2015-09-21彭丽霞刘玉宝潘林林曹一家
杜 杰,彭丽霞,刘玉宝,潘林林,王 雷,曹一家
(1.南京信息工程大学 计算机与软件学院 江苏省大气环境与装备技术协同创新中心,江苏 南京 210044;2.南京信息工程大学 教育部互联网应用示范基地 江苏省网络监控中心,江苏 南京 210044;3.南京信息工程大学 大气科学学院,江苏 南京 210044;4.美国大气研究中心,美国 博尔德 80301;5.国电南瑞科技股份有限公司,江苏 南京 211106;6.湖南大学 电气与信息工程学院,湖南 长沙 410082)
0 引言
风电场风机测量风速的完整性无论对于研究风电场出力、还是对于研究风机布局以及风机紊流影响等都具有重要意义[1-3]。为了开发更加精确的风电场出力预报系统,美国大气研究中心NCAR(National Center for Atmospheric Research)着手研究精细化预报系统,完整的风电场风机风速采集数据是这一系统顺利实施的关键环节之一[4]。但是针对美国科罗拉多州某风电场的风机测量风速进行分析发现,最突出的问题是有缺损的数据,时间跨度从10 min至几小时。虽然通过一些策略,如持续法和插值法可以填充这些缺损的数据,但持续法假设风速不变,插值函数的非线性特性很难与风速变化趋势一致,使得缺损值填充效果不好。现有研究表明风力数据的缺失对风电的预估产生重要影响,必须加以考量[5]。
针对风电场测量风速缺损值的填充方法,目前大多围绕空间相关性展开,用邻近站点的测量数据进行补缺[6-8]。通过分析该风电场实际工况,可发现以上文献的填充方法面临全新的考验。首先,由于风电场内多台相邻风机共用一条数据传输线路,当发生传输故障时,往往风电场内相邻多台风机同时发生风速缺测的工况,使得填充所参考的邻近风机的测量风速不存在,影响模型精度;其次,由于该风电场风机众多,如果考虑到风电场地势高低起伏的地理环境、风机的尾流效应,以及季节对风速风向的影响等因素,风电场中邻近风机的风速很难保证强相关性。因此缺乏单一有效的缺损风速值填充模型。
本文引入动态时间规整DTW(Dynamic Time Warping)算法,结合空间邻点 SNN(Spatial Nearest Neighbor)法和 Pearson相关系数 PCC(Pearson Correlation Coefficients)法,分别搜寻与缺损测量风速风机风速演化最为相似的若干台风机及对应的测量风速时序,构建小波神经网络的训练集,进行单个模型的风速缺损值填充实验,然后挑选出较好的模型进行基于熵权的组合,进一步提高填充精度。实验结果表明,本文方法对于风电场内邻近多台风机同时缺测风速的工况,填充效果明显优于现有方法。本文方法针对风电场内所有风机进行测试,因此具有普适性。
1 风机测量风速非线性分析
研究的风电场位于科罗拉多州北部,共274台风机,编号1至274号,风机分布于落基山麓,每2台风机间隔400~700 m,风机分布如图1所示,所采集的风机测量风速数据时间跨度从2008年10月23日至2009年1月31日,采样间隔10 min。
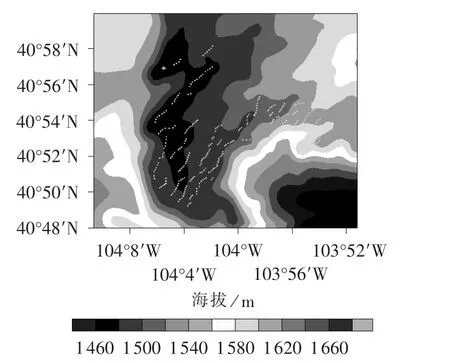
图1 科罗拉多州东北部Xcel能源公司风电场风机分布Fig.1 Layout of wind turbines in wind farm of Xcel Energy Company at northeastern Colorado
本文随机选取8号风机风速时间序列,经计算其Hurst指数H=0.876,表示系统存在长期记忆性,具有分形的特点[9]。重构相空间、构造递归图是最直接的研究混沌系统可预测性的方法之一,分别采用互信息法[10]和小数据量法[11]计算延迟时间τ=5 和嵌入维数m=5,由此计算出的递归图如图2所示[12]。可见,在前500个采样点,平行于主对角线的直线段较多,但比较凌乱,长度短;而600~800采样点区间几乎没有这样的直线段,意味着本风电场风速的混沌特性并非全时间区域,具有很强的分段特性且不显著,因此采用重构相空间的建模方法对于本风电场不太合适。
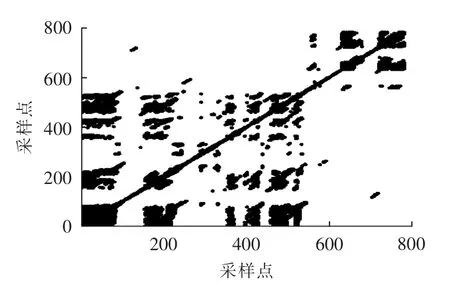
图2 8号风机测量风速递归图Fig.2 Recurrence figure of wind speed measurements for No.8 wind turbine
2 风速缺损值小波神经网络组合填充模型
2.1 模型思路
本文所做的实验表明该风电场风机测量风速呈现复杂的弱混沌特性,不适合从重构相空间的角度来研究。本文最主要的工作在于从二维时间域上采用多种方法对风速时间序列的相似性进行分析,提取最相似的若干台风机的测量风速,引入对于该类时间序列泛化性能较优的小波神经网络,构建基于熵权的缺损风速小波神经网络组合填充模型。
2.2 邻点判别方法
(1)SNN 法。
采用大圆距离计算两风机距离 d(i,j),其中 i、j为风机编号。d(i,j)越小说明i号和j号风机在空间上越靠近。
(2)PCC 法。
采用积差方法,以两变量与各自平均值的离差为基础,通过2个离差相乘来反映两变量之间相关程度 R(i,j)。 R(i,j)越大说明 i号和 j号风机的采样风速时序线性相关性越强。
(3)DTW 算法。
DTW算法研究两时间序列经拉伸和收缩后的相似性问题[13]。进行DTW计算的两风速时序可以不等长,符合风速测量的实际工况;同时,将2条风速时序在时间轴上进行拉伸/收缩的非线性映射,更符合形态相似、但发生时刻和发生幅度不一致的风速的实际工况,因此其理论基础特别适合于风的处理。
假设i号和j号风机的采样风速数据分别为I={I1,I2,…,It,…,IN}和 J={J1,J2,…,Jt,…,JN},其中,N为采样点的个数。构造矩阵dN×N,其中dN×N的每一个元素为:
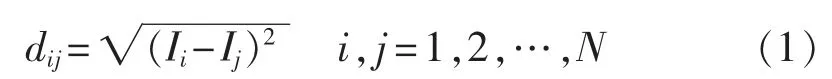
在矩阵dN×N中,把相邻的矩阵元素的集合称为弯曲路径,记为 W= {w1,w2,…,wk,…,wK},W 的第 k个元素 wk=(i,j)k,这条路径满足下列条件:
a.N≤K<2N-1;
b.w1=(1,1),wK=(N,N);
c.对 wk=(i,j)、wk-1=(i′,j′),满足 0≤i-i′≤1、0≤j-j′≤1。
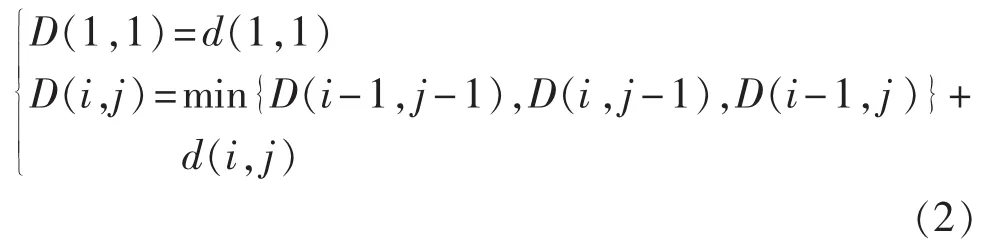
DTW(I,J)越小,说明 i号和 j风机测量风速在时间轴上伸缩后相似度越高。
2.3 小波神经网络算法及改进
小波神经网络是以小波函数为基底的神经网络,结合了小波变换良好的时频局部化性质和传统神经网络的自学习功能,具有较强的逼近和容错能力,适合风速快速变化的特性[14]。
本文采用3层小波神经网络结构,Morlet母小波基函数,学习方法采用增加动量项的梯度下降法,但是在学习目标上不采用传统的迭代次数或误差精度的衡量标准。原因在于风的波动性大,传统的学习方法不易达到训练的精度要求,导致神经网络训练次数往往会达到设定的上限,容易造成对于训练集的过学习,反而降低了神经网络的泛化性能;降低训练的精度要求又会使得神经网络对训练集学习不充分,影响模型效果。因此,本文以前后2次训练的累积误差的比值为衡量标准。其依据和优点为:
a.梯度下降法前后2次迭代的累积误差比值越接近1,说明此时的神经网络对于样本的训练误差下降有限,训练基本达到目标,如果继续训练,增加了模型对于样本的过学习,若此时结束训练,模型尚未出现过拟合的情形;
b.以神经网络2次训练累积误差比值作为衡量标准,避免了对于不同学习样本,需设定不同的学习精度或者最大迭代次数的不便,更加适合于波动性剧烈的风速的建模。
经实验,以2次训练累积误差比值达到0.993作为结束训练的判定标准。本文的学习方法普遍在学习20~40次就达到训练目标,极大地缩短了训练时长,同时提高了模型的泛化性能。
2.4 基于信息熵的组合填充模型
熵是系统信息量的度量,熵越大,系统的信息量越小,系统的变异程度也越小。本文利用熵来衡量单项填充方法对历史风速的拟合误差序列的变异程度,若变异程度越大,则在组合填充中对应的权系数就越小[15]。 具体过程如下。
a.记第i种单项方法在第t步长时的相对填充误差eit的比重pit为:
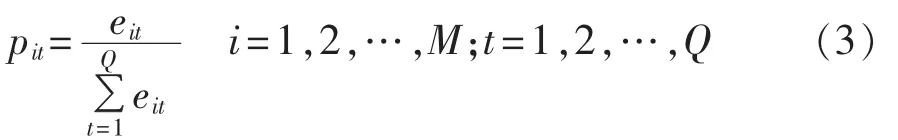
其中,M为填充方法总数;Q为总的填充步长。
b.计算第i种单项方法的相对填充误差的熵hi:
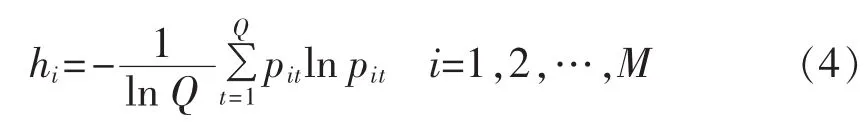
c.计算第i种单项方法相对填充误差序列的变异程度系数di:
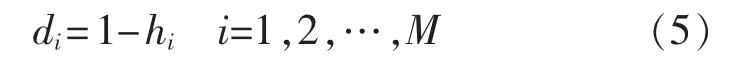
d.计算各单项方法在组合模型中的加权系数大小 ωi:
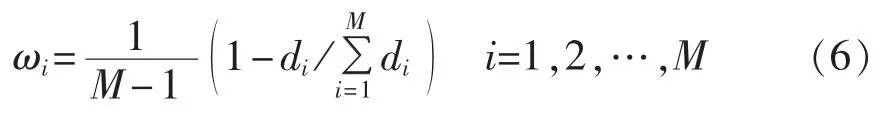
e.计算组合填充值。
3 计算实例与分析
分别以SNN法、PCC法和DTW算法为衡量标准,寻找与缺损测量风速风机在缺损采样点附近风速演化相似的风机,并以其相对应的风速时序构建神经网络训练集和测试集,进行风电机测量风速缺损值的模拟填充实验。对风电场内所有274台风机进行模拟填充,选取前800个没有缺损值的数据集作为测试集,以第650个采样点为开始,每隔1 h,共模拟了 650、656、662、668、674、680 这 6 个缺损测量风速起始点,每个测试点进行20个步长的缺损值填充实验,并以平方误差和(SSE)衡量各个方法的效果:
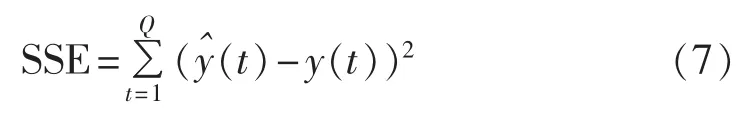
3.1 实验1:模型参数的确定
本模型需确定以下2组参数。
a.用于衡量风速演化相似性的风速时序长度。
除SNN法外,PCC法和DTW算法都需要确定进行相似性比较的风速数据的长度Len。基于风速的高度非线性,Len过短只是针对超短时相似性度量,过长则是长时平均相似性,此处最要衡量的是填充起始点前后的风速相似性。
b.神经网络的输入层-中间层节点数。
神经网络的学习效果与训练集密切相关,当训练集与建模对象强相关时,建模效果也较好。此处神经网络的输入层神经元个数即为与缺损测量风速风机风速演化最相似的风机的台数,而训练集则为这些风机的测量风速。
风电场内274台风机有6个模拟缺损值发生点,针对以上3种填充方法,分别构建小波神经网络模型PCC_NN、DTW_NN和SNN_NN,输入层节点数nInput_NN为3~6,中间层节点数nMiddle_NN为nInput_NN+1~2nInput_NN+3,Len从 1 h(6 个采样点)至 20 h(120 个采样点)。本文采用C语言编写相应的代码,采用MPI构造并行运行环境,在南京信息工程大学高性能计算中心进行计算,对所有结果进行统计,发现当nInput_NN为4、nMiddle_NN为9时,神经网络的泛化能力最优。并且,依据SNN_NN和DTW_NN,SSE随着 Len的增加迅速降低,并在Len为11 h时基本达到最低值,之后变化缓慢。 因此,选择 nInput_NN=4、nMiddle_NN=9、Len=11 h(66个采样点)进行风电场风机缺损风速的填充实验。
3.2 实验2:邻近风机同时缺测风速时的填充效果
因为风电场中相邻的若干台风机共用一条传输线,因此当数据采集或者传输环节出现问题,往往会导致多台风机同时缺测风速的发生,目前已发表文献均未研究此种工况。本文测试了当风电场内相邻多台风机同时发生缺测风速的工况下,选择实验1确定的模型参数,并以相邻缺测风速风机台数等于3时,对3种方法的效果进行对比,结果如表1所示。
由表1可见,DTW_NN模型无论是SSE,还是最小SSE占比,都要远好于另外2种模型,原因在于DTW算法本质上衡量的是风速时序在时间轴上的非线性相似性,PCC法是线性相关性法则,而风速是强非线性的;SNN法仅仅以空间距离为标准,当邻近风机都缺损测量风速时,其填充效果最差,但是,DTW算法在最小SSE占比上并不占绝对优势。
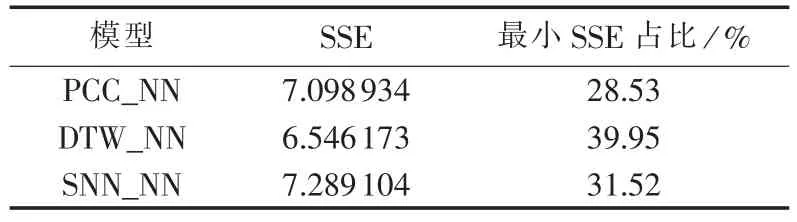
表1 邻近3台风机同时缺测时3种模型补缺效果对比Table1 Comparison of wind speed measurement interpolation for three adjacent wind turbines among three models
3.3 实验3:组合填充效果
选择PCC_NN、DTW_NN和SNN_NN模型,以实验1确定的模型参数,模拟相邻缺测风速风机台数为3~10,共8组实验,构造基于信息熵的组合填充模型ECF_NN。实验取各模型针对补缺起始点前20步风速的预测值作为组合模型确定权重的训练集,20步填充SSE如图3所示。首先,组合模型的3个子模型中,DTW_NN模型的精度最高,其20步填充SSE均值为6.9668,较PCC_NN模型降低了14.11%,较SNN_NN模型降低了13.32%;其次,ECF_NN精度最高,且SSE波动小,其20步填充SSE均值为5.9909,较DTW_NN模型降低了14.01%。
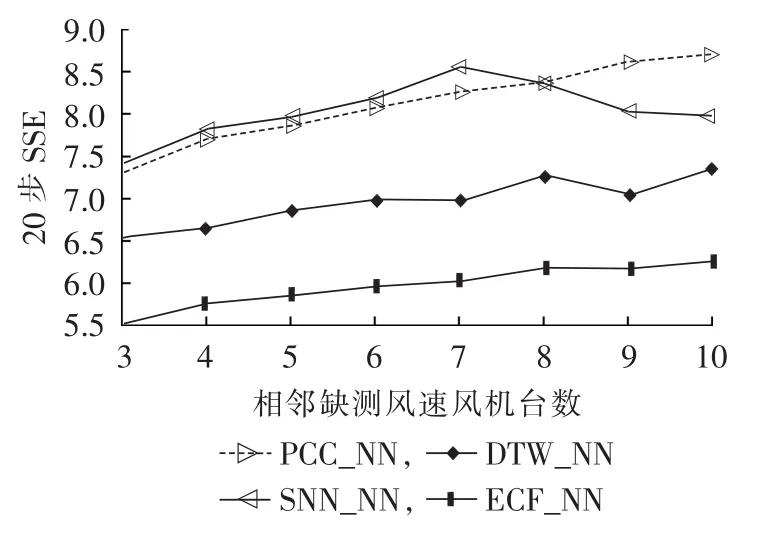
图3 4种模型填充效果对比Fig.3 Comparison of interpolation results among four models
3.4 实验4:对比实验
最后,以8号风机为例,采用本文提出的组合模型与差分自回归移动平均模型ARIMA(Auto Regressive Integrated Moving Average model)以及持续法进行对比。ARIMA模型识别中,8号风机风速时序经过1阶差分之后达到平稳,通过AIC准则定阶法确定为ARIMA(2,1,2)结构。 选取第 270 点作为缺损测量风速起始点,填充结果如图4所示:组合填充法的SSE最小,为 19.8891;ARIMA 法 SSE为71.1221;持续法的SSE最大,达到174.6365。对所有274台风机6个填充起始点进行填充实验,模拟每一台风机邻近3~10台风机同时缺损测量风速,如表2所示,可见,本文的组合模型的SSE最小,当邻近3台风机同时缺测风速时,其SSE仅为5.53,而当邻近有10台风机同时缺测风速时,其SSE也仅为6.27,而ARIMA法和持续法的SSE分别达到16.29和21.56。
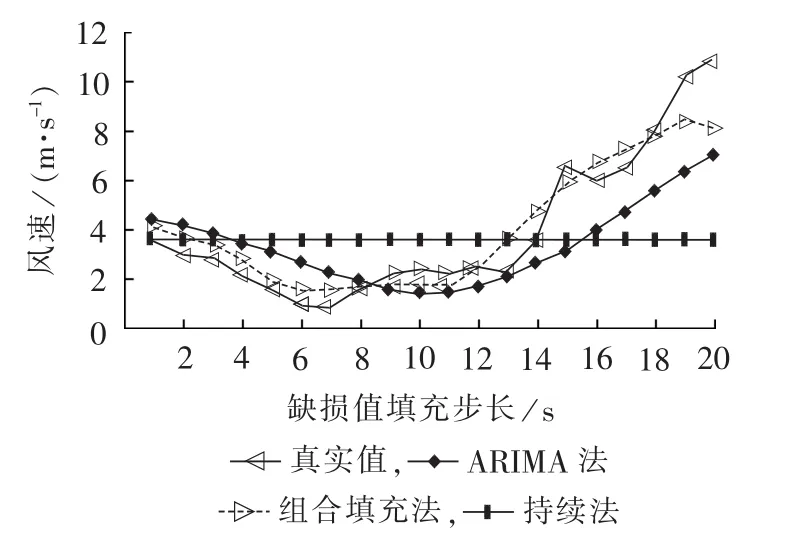
图4 8号风机风速补缺实验结果Fig.4 Experimental results of wind speed interpolation for wind turbine No.8
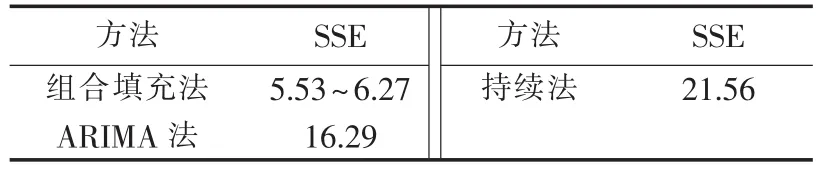
表2 实际风速与3种方法风速补缺对比Table 2 Comparison between actual and interpolated wind speeds for three methods
4 结论
针对风电场内邻近多台风机同时缺损测量风速的工况,采用DTW算法,结合PCC法、SNN法,从二维时间域搜寻与缺损测量风速风机风速演化最为相似的若干台风机,利用这些风机的风速构建神经网络,并在此基础上建立基于信息熵的组合填充模型。
a.针对风电场内邻近多台风机同时缺损测量风速的工况,由于DTW算法衡量的是风速在时间域上经收缩/拉伸的非线性相似性,因此在补缺效果上要好于基于线性相关性的PCC法和SNN法。
b.改进的小波神经网络模型以2次训练累计误差比作为神经网络学习指标,缩短了训练时间,避免了过学习的发生,更加适合于波动性剧烈的风速的建模。
c.实验表明,组合填充模型的填充误差最小,风电场内274台风机所做的实验增加了本文算法的普适性。
