基于自适应分支系数的并网光伏电站接地距离保护

张 尧，晁 勤，王厚军，李育强，王一波

（1.新疆大学 电气工程学院，新疆 乌鲁木齐 830046；2.新疆工程学院，新疆 乌鲁木齐 830091；3.国网新疆供电公司 昌吉电业局，新疆 昌吉 831100）

0 引言

国际、国内光伏发电市场发展迅速，以并网发电和离网发电2种方式共存，其中并网方式以90%的份额占主导地位。目前我国青海格尔木并网光伏电站的容量已达300 MW，计划到2020年，青海省将形成7500 MW的光伏并网发电量。随着并网光伏电站容量的增加，光伏电站升压接入110 kV电网提供的短路电流也在不断增加，对110 kV电网的距离主保护影响很大，不容忽视。因此光伏电站接入110 kV电网对距离保护的影响及应对措施研究非常必要。

现有关于光伏电站并网对保护影响的研究，主要集中在对电流保护的影响和应对措施方面[1-5]，对距离保护的影响研究较少。文献[6]以双馈风电场为研究背景，分析得出基于工频傅氏算法的相量距离保护元件由于风电场送出线电压、电流主频不同而影响其动作性能。文献[7]分析了分布式电源接入配电网对并网联络线保护的影响，指出由于分布式电源归算至并网变110 kV母线侧的阻抗过大，分布式电源侧的距离保护有可能拒动，会威胁到变压器的绝缘安全。文献[8]指出分布式电源的正向助增电流会使距离保护Ⅱ段范围缩小，可能降低其灵敏度，但未进一步探讨分支系数的改进方法。文献[9]对光伏电站的等效阻抗用标准测试条件下的开路电压乘以串联个数与短路电流乘以并联个数的比值来确定。但是由于光照和温度等实际运行条件与标准测试条件存在差异及各部分光伏阵列特性不一致[10]，光伏电站的等效阻抗可能存在较大误差。

因此本文首次提出一种新思路——构建正常运行实测光伏电站发电量P和光伏电站等效阻抗XG2与接地距离保护分支系数Kf三者之间的相互关系模型，进而确立自适应接地距离保护整定判据。本文采用序分量原理，以及目前光电逆变器直流侧电压和交流侧电流短路时若超过额定值20%将会损坏逆变器的特性，研究P、XG2、Kf三者之间对应关系的规律，既避免光伏电站等效阻抗可能存在的误差，又获得光伏电站发电量P与分支系数Kf的定量关系系数，并定量给出了分支系数Kf的修正值；采用自适应原理建立了接地距离Ⅱ段阻抗整定值判据。仿真验证结果表明该方法有效、实用。

1 基于序分量原理建立光伏电站等效阻抗XG2与分支系数Kf间的关系模型

光伏电站的接入使得原来的单电源网络变成多电源网络，构成助增电源的情形。由于光伏电站具有不同于常规电源的P-I特性，提供的短路电流偏小，使得原来按最小分支系数确定的接地距离保护的保护范围变小，降低了距离保护的性能。

合理地确定分支系数，可弥补接地距离保护范围变小的不利因素。本文以图1所示的新疆某地区光伏电站电网构架为例，采用序分量原理推导并建立光伏电站等效阻抗XG2与分支系数Kf的模型。

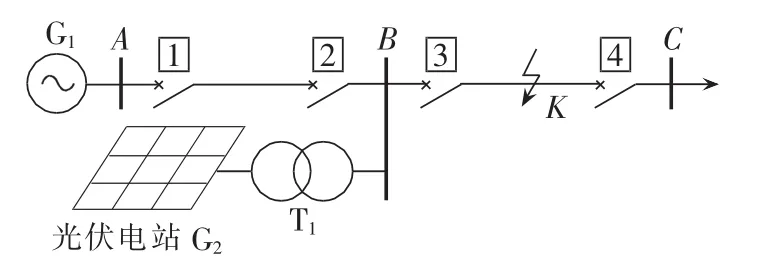
图1 某实际光伏电站结构Fig.1 Structure of an actual PV station

如图1所示，光伏电站接入母线B时，对于母线A处的距离保护Ⅰ段，由于其只保护线路AB的85%，因此不受光伏电站的影响。而距离保护Ⅱ段保护范围要覆盖本线路全长，必须延伸到线路BC，当K点发生单相接地短路时，由于光伏电站的接入形成助增电源，保护装置1的距离保护Ⅱ段测量到的电压与电流的比值大小不再与距离长短成正比。因此需要考虑光伏电站引起的助增分支系数的影响。

保护装置1的A相电压采用序分量表示为式（1）：

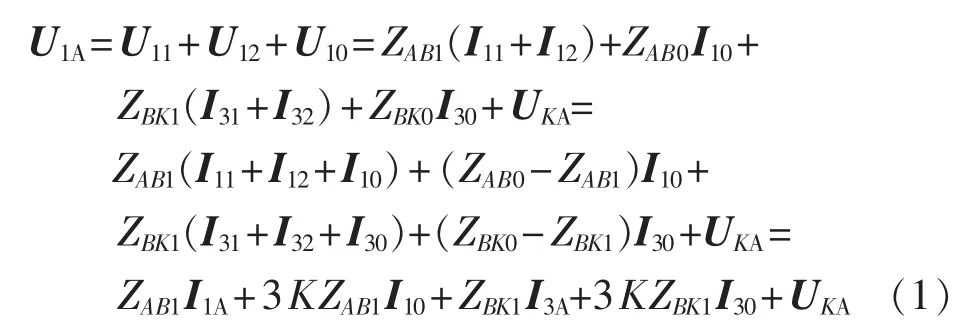
假设线路发生金属性短路，那么保护装置1的测量阻抗为：

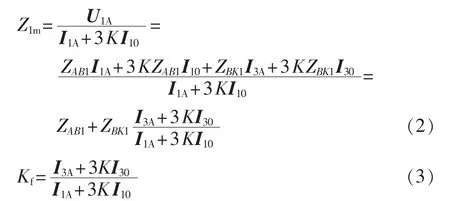
其中，Kf为分支系数。

采用序分量法可将分支系数式（3）转化为：

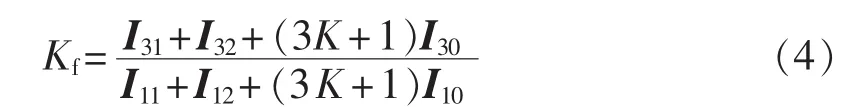
其中，I11与I31之间关系根据图1推导为式（5）：

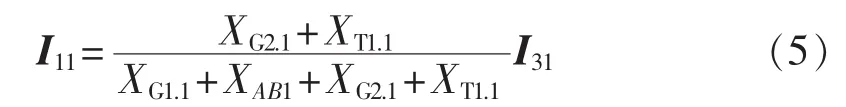
当K点发生单相接地故障时有：

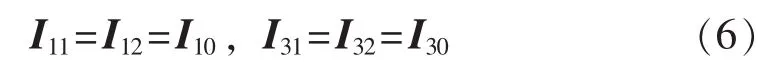
将式（5）、（6）代入式（4），化简后得出光伏电站等效阻抗XG2.1与分支系数Kf之间的关系模型为：

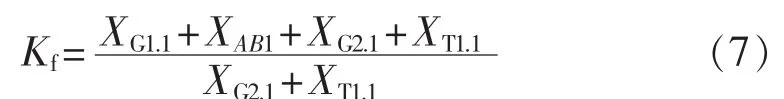
其中，XG1.1、XT1.1、XAB1分别由等效电源 G1、变压器 T1、线路AB的阻抗正序分量决定，其值为定值；光伏电站阻抗XG2.1随光照强度和温度变化，由阻抗的正序分量组成，故等价为光伏电站等效阻抗XG2。

2 确定光伏电站发电量P与分支系数Kf的对应关系

图2为并网光伏电站的简化电路图，由数十个光伏组件+逆变器组并联组成，经过升压变压器实现高压交流输电[6]。众所周知，光伏电站发电量P随光照强度增大而增大，光伏电站等效阻抗XG2与光照强度也存在一定关系，确定等效阻抗XG2与发电量P之间的对应关系，是分析光伏电站发电量P与分支系数Kf间关系的前提[11-13]。

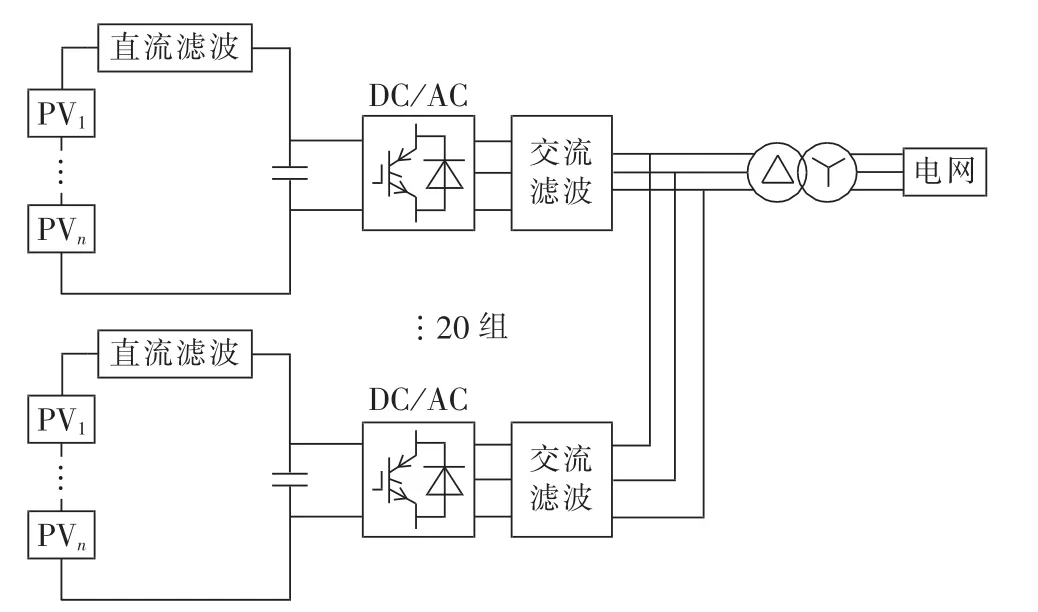
图2 并网光伏电站的简化电路Fig.2 Simplified circuit of grid-connected PV station

2.1 光伏电站发电量P与等效阻抗XG2相关性分析

2.1.1 光伏电站等效阻抗XG2计算方法

工程用光伏组件数学模型[14-16]如式（8）、（9）所示。

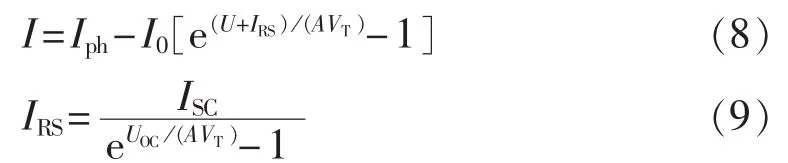
其中，Iph为给定光照下的短路电流；A为二极管理想常数；VT为组件热势能；UOC为开路电压；ISC为短路电流。

若光伏电站等效阻抗用式中的光伏电池组件输出电流I、输出电压U推导确定将存在较大误差，可能的原因为：开路电压UOC和短路电流ISC是在标准测试条件，即温度Tref=25℃、光照强度Gref=1000 W/m2下测试的，与光照等实际运行条件存在差异；数十个光伏组件+逆变器组并联组成的各部分光伏电池特性的不一致，使得组合输出特性为多峰值P-U曲线。因此本文采用现场实测值确定光伏电站等效阻抗以适应各种不同光照和温度等运行方式的改变。

根据图2可知1组光伏组件与逆变器是串联关系，因此1组光伏组件+逆变器的等效阻抗X′G2可由在不同光照强度下DC/AC直流侧实测电压与实测电流的比值叠加交流侧实测电压与实测电流的比值近似求取，再根据图2所示各组光伏组件+逆变器为并联关系求取光伏电站的总等效阻抗XG2，如式（10）所示。

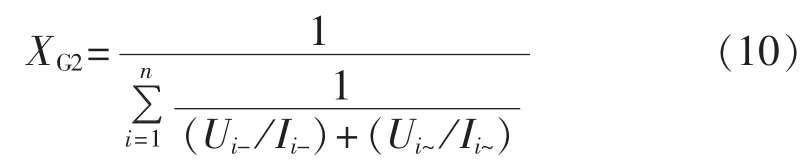
其中，Ui-、Ui～分别为第i组光伏组件+逆变器的直流侧和交流侧实测电压；Ii-、Ii～分别为第i组光伏组件+逆变器的直流侧和交流侧实测电流；n为光伏组件+逆变器并联组数。

2.1.2 P-XG2相关性分析及建模

由实测数据可获得不同光照强度下每组光伏组件+逆变器的输出功率，对各组光伏组件+逆变器的输出功率求和即为光伏电站发电量P，由式（10）可得光伏电站等效阻抗。由于光伏电站发电量P随光照强度增大而增大，因此也随输出电流增大而增大，而输出电压变化幅度较小，表明光伏电站等效阻抗XG2随发电量P的增大而减小，其变化趋势如图3所示。

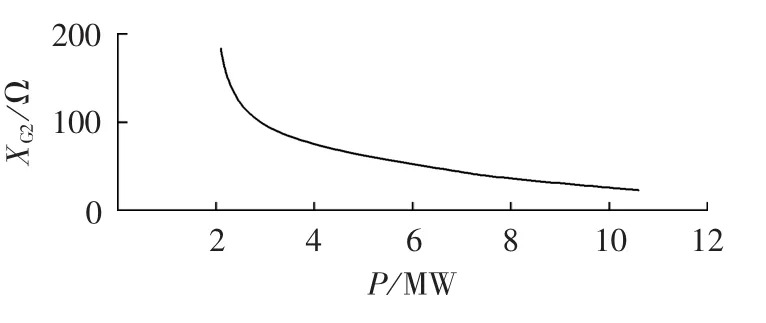
图3 光伏电站发电量P与光伏电站等效阻抗XG2的关系Fig.3 Relationship between P and XG2

若根据实测数据及式（10）绘制并计算出反映光伏电站实际P-XG2关系的曲线图，可采用曲线拟合法求解P-XG2模型：

其中，α、β在具体算例验证中确定。

2.2 基于P、XG2、Kf三者之间对应关系构建P-Kf模型

由前面推出的 XG2、Kf之间的关系式（7）和 P、XG2之间的关系式（11），可获得 P、Kf之间的关系模型为：

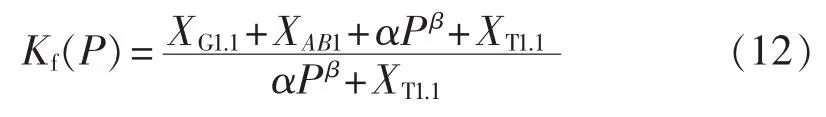
3 基于自适应原理建立接地距离保护判据

如图1所示的保护装置1距离保护Ⅰ段由于不受光伏电站的影响，按原保护定值整定，公式略。距离保护Ⅱ段若按原保护定值整定，最小分支系数必定取1，意味着光伏电站的发电量P为0，有可能造成接地距离保护Ⅱ段拒动，因此按照P、Kf之间的关系式（12），建立基于分支系数自适应的接地距离保护Ⅱ段整定值式（13）及保护判据式（14）：

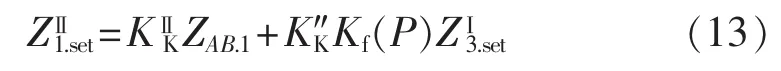
其中，P的单位为MW；ZⅡ1.set为保护装置1的接地距离保护Ⅱ段的整定值；KⅡK、K″K为距离保护Ⅱ段可靠系数；ZAB.1为线路AB的正序阻抗；ZⅠ3.set为保护装置3的接地距离保护Ⅰ段的整定值；Z1m为保护装置1的测量阻抗。

4 算例验证

新疆某地区额定功率为10 MW的光伏电站，采用500 kW的逆变器并网，有20组逆变器并联。光伏电站的输出电压是415 V，经箱式变压器升到35 kV，再经总变压站升到110 kV，汇入110 kV电网。

线路BC长50 km；等效电源G1的各序阻抗为XG1.1=XG1.2=15 Ω；变压器T1的各序阻抗为XT1.1=XT1.2=10 Ω，XT1.0=30 Ω；线路各序阻抗为 Z1=Z2=0.4 Ω/km，Z0=1.2 Ω /km。

表1为2014年7月5日新疆某地区10 MW并网光伏电站2号逆变器直流侧交流侧实测数据，限于篇幅，其余组实测数据略。由表1可知，实测数据与不同光照强度光伏模块的电流电压特性曲线[8]吻合；不同光照强度下的直流侧电压电流和交流侧电压电流均不同，随着光照强度的减弱，电流也随之减小，电压变化不大。

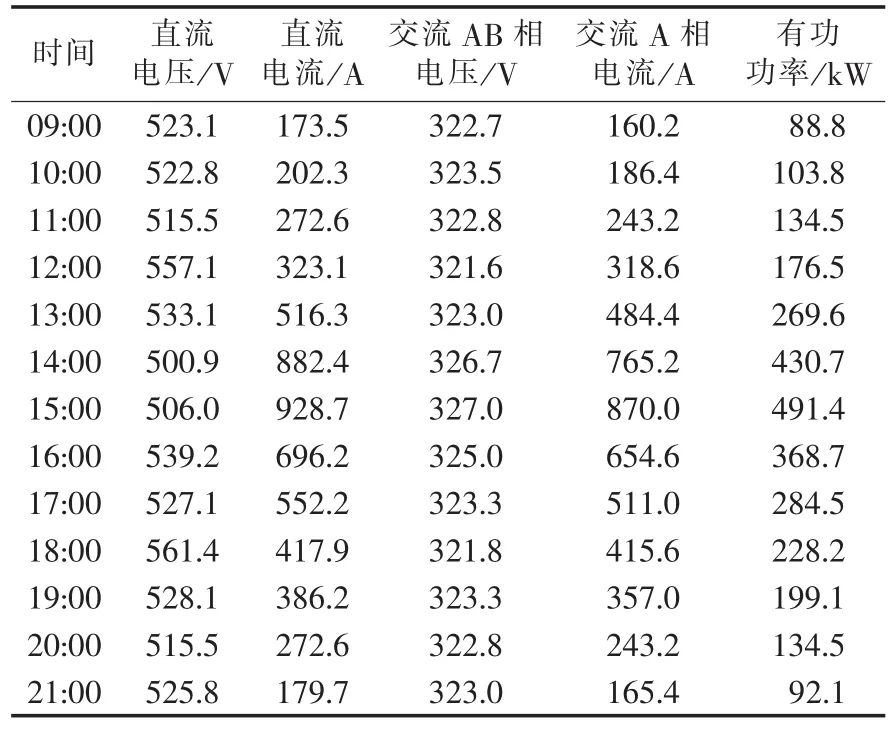
表1 2号逆变器直流侧和交流侧数据Table 1 DC-and AC-side data of inverter No.2

4.1 确定P-XG2关系模型中的α、β

将表1中的直流电压电流和交流电压电流代入式（10）中的分母得到1组光伏组件+逆变器的等效阻抗X′G2。选取一部分典型运行数据见表2，表中用箭头的多少表征光照强弱。

将同一时刻20组逆变器直流侧交流侧数据代入式（10）得到XG2，同时将20组逆变器的输出有功功率相加得到 P，取 α=3507.5、β=-1.03，采用曲线拟合法求解得：

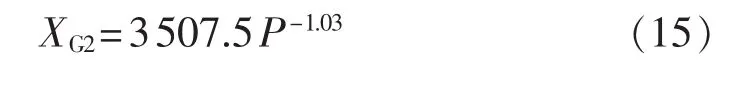
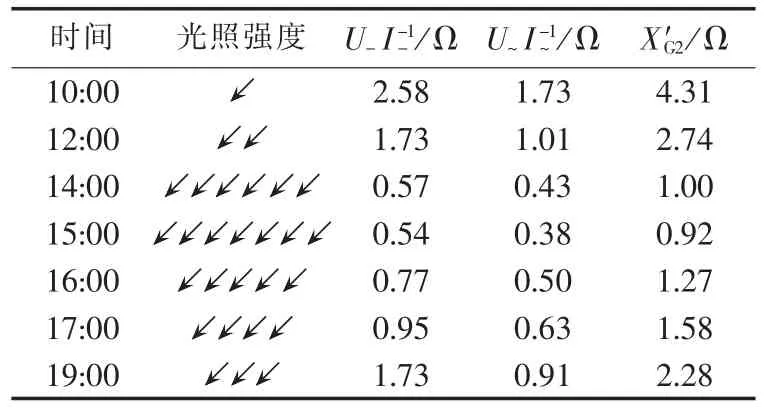
表2 2号逆变器直流侧数据及1组光伏组件+逆变器的等效阻抗Table 2 DC-side data of inverter No.2 and equivalent impedance of PV module group and inverter

4.2 P、XG2、Kf三者之间对应关系验证

由表1和式（1）联立求解可获得光伏电站P、XG2、Kf三者之间的关系，如表3所示。

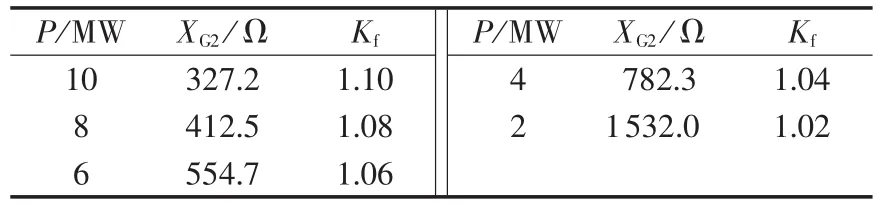
表3 P、XG2和 Kf的关系Table 3 Relationship among P，XG2and Kf

通过表3可知光伏电站等效阻抗变化范围较大，比常规电源的阻抗变化范围大很多。光伏电站等效阻抗XG2随着光伏电站发电量P的增大而减小，相应的分支系数Kf却增大。

确定光伏电站发电量P与分支系数Kf的相关系数，是实现光伏电站接入电网自适应距离保护的前提。由图4可知Kf和P基本符合线性关系，其斜率为0.01/MW左右，可简化为：

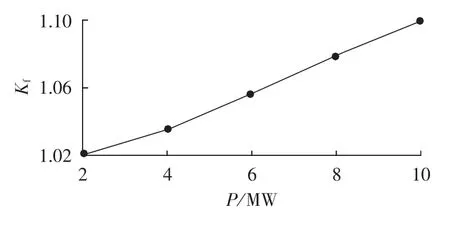
图4 P与Kf的线性关系Fig.4 Linear relationship between P and Kf

4.3 自适应距离保护Ⅱ段验证

已知光伏电站发电量 P，由式（13）和（16）求解得ZⅡ1.set，如表4所示，表中，保护范围指其和线路AC的百分比。

自适应接地距离保护整定值根据光伏电站发电量P的变化，自动调整分支系数，使距离保护性能处于更好状态，比原距离保护的保护范围显著增大，提高了保护的灵敏度。

保护装置3的距离保护Ⅰ段时间整定为0 s，保护装置1的距离保护Ⅱ段整定时间为0.5 s，满足保护装置1的距离保护Ⅱ段与保护装置3的距离保护Ⅰ段间保护范围和时间的配合要求。保护装置1的距离保护Ⅲ段按负荷阻抗整定，它的整定值远比距离保护Ⅱ段大，自然满足与Ⅰ段和Ⅱ段的协调配合关系。

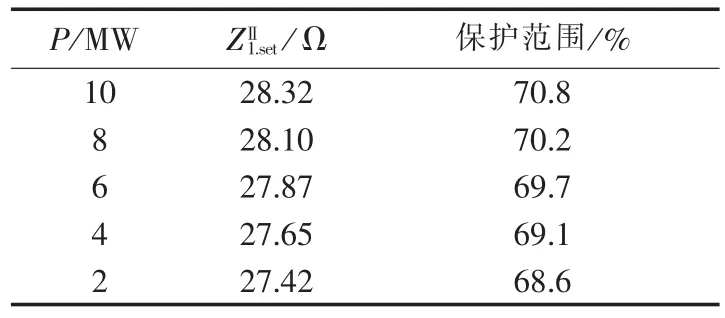
表4 P、ZⅡ1.set及保护范围的关系Table4 Relationship among P，ZⅡ1.setand protection range

5 结论

本文推导出光伏电站等效阻抗XG2与分支系数Kf间的关系模型，利用光伏电站逆变器直流侧电压、电流和交流侧电压、电流数据，分析了光伏电站发电量P与等效阻抗XG2间的关系，以光伏电站等效阻抗XG2为桥梁，发现P、Kf间基本呈现线性关系，从而建立了自适应接地距离保护Ⅱ段阻抗整定值判据。