互联电网静态电压稳定预防控制模型及其算法

户秀琼 ，颜 伟 ，余 娟

（1.四川省攀枝花学院 电气信息工程学院，四川 攀枝花 617000；2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

随着我国电力建设的发展，六大跨省电网的建成使我国电力系统已经发展成了大规模互联电网。互联电网在带来巨大经济效益的同时，也使得电网的主干线路经常运行在稳定极限的边缘，产生了一些新的引起电压失稳甚至系统崩溃等问题的因素，增加了互联电网发生电压失稳事故的可能性[1-2]。特别是在故障和／或重负荷的双重作用下，重载薄弱支路所传输的功率极易超过其传输能力，使得互联电网失去潮流可行解或潮流平衡点，引发静态电压失稳事故，最终导致损失大量负荷甚至系统瓦解[3-5]。因此，采取有效的预防控制措施来改善当前互联电网的运行状态，以保证其在正常运行状态、预想故障以及重负荷情况下的静态电压稳定性具有重大实际意义[3-4]。

现有针对静态电压稳定问题的预防控制已经取得了较多的研究成果[6-10]，但针对互联电网静态电压稳定问题的预防控制却少有研究。文献[11]提出了大型互联电网的静态电压稳定预期电压控制策略。该策略针对不满足静态电压稳定裕度要求的关键时段，建立了预期电压控制优化模型，约束条件包括关键时段所对应的系统基态潮流等式约束、静态电压稳定裕度约束以及系统各控制量的运行约束；并采用集中式优化算法求解。文献[11]所提预期电压控制的思想与电压稳定预防控制的思想类似，但其针对的是某些不满足静态电压稳定裕度要求的预测时段，而预防控制则是针对某些不满足静态电压稳定裕度要求的预想故障。

然而，在电力市场环境下，互联电网为了实现更大范围的资源优化配置，同时在更大的市场内进行竞争，在保证其静态电压稳定性的同时，各区域间传输断面功率还必须调整至指定值以满足交易功率约束，但文献[11]却没有考虑这个问题。

另外，在互联电网中，文献[11]所采用的集中式算法存在数据实时收集困难、数据资源异构、数据通信量及存储量大等缺点。而分布式算法则能够根据各子网内部的局部数据和目标独立进行计算，数据通信量及存储量小，在避免内部重要数据外泄的同时，又能保证全局仿真分析的精度和速度要求。因此，分布式算法已经成为解决多区域互联电网一体化仿真计算的重要工具和手段。

在目前已有的分布式算法中，辅助问题原理APP（Auxiliary Problem Principle）算法应用最为广泛[12-14]，但其研究至今还不成熟，在突破凸函数的理论限制、提高算法收敛性能和稳定性方面还需要做进一步深入研究。文献[15]将分解协调内点法与APP算法进行了比较，发现分解协调内点法在计算时间、目标函数的精确性、迭代次数方面均比APP算法具有优势。

鉴于此，本文提出考虑断面功率约束的互联电网静态电压稳定预防控制优化模型及其算法。该预防控制模型以控制代价最小为目标，其约束条件包含正常运行状态以及各预想故障状态下区域电网间传输断面的功率约束。针对互联电网分层分区管理的特点，根据所提优化模型进一步建立互联电网静态电压稳定预防控制的分解协调优化模型，并采用分解协调内点法求解，以此降低模型的求解难度，提高其求解效率。

1 互联电网静态电压稳定预防控制模型

对于互联电网的静态电压稳定预防控制而言，不但要考虑正常运行状态下的运行约束以及预想故障状态下的静态电压稳定裕度约束，还应该考虑各运行状态下区域电网间传输断面的功率约束。而断面传输功率的设定值在正常运行状态下以及预想故障状态下可能会因为系统的调节能力不同而不同。因此，本文所建立的互联电网静态电压稳定预防控制数学模型具体如下所述。

1.1 目标函数

静态电压稳定预防控制的目标往往是以尽可能小的控制代价保证系统在正常运行状态及预想故障状态下均具有足够的静态电压稳定裕度。其控制措施包括调节发电机有功和无功出力、投切可调电容器和电抗器、调节有载调压变压器分接头以及切负荷[7]。因此，本文所提预防控制优化模型的目标函数如下：

其中，PGi、QGi、QCi、QRi、kt分别为发电机有功出力、无功出力、可调电容器注入无功、可调电抗器注入无功、有载调压变压器变比，当前运行状态下（预防控制之前的正常运行状态）的运行变量以下标“0”表示，预防控制后正常运行状态下的变量以上标“0”表示；Ci为负荷节点所切有功负荷量；NG、NB、NC、NR、NT分别为发电机节点数、系统节点数、可调电容器组数、可调电抗器组数、有载调压变压器台数；wpi、wqi、wri、wci、wkt、wli分别为各个控制措施的权重，在实际工程中，一般而言，发电机的有功和无功调节成本相对较低，因此其权重可取为0.1，而可调电容器、可调电抗器、有载调压变压器的调节成本相对较高，其权重可取为1，切负荷的调节成本比其他控制措施的调节成本稍大一些，其权重可取为 10[7]。

1.2 正常运行状态下的可行性约束

预防控制后的互联电网需要满足正常运行状态下的可行性约束以及区域电网间传输断面的功率约束，如式（2）—（13）所示。

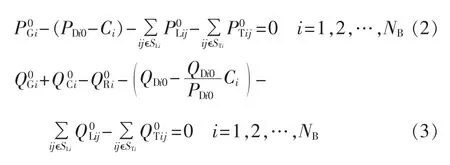
其中，PDi、QDi分别为系统各节点有功、无功负荷；Ui、ei、fi分别为系统节点电压幅值及其实部与虚部；em、fm分别为有载调压变压器支路引入的虚拟节点电压相量实部和虚部[16]；Ncut为电网中联系各个子网的断面个数；Slink，n为区域电网间第n个断面所包含的联络线的集合；SLi为与节点i相连的线路支路集合；STi为与节点i相连的有载调压变压器支路集合；Pcut，n为区域电网间第n个断面的有功功率设定值；Pij，n为区域电网间第n个断面中的联络线上传输的有功功率；PLij、QLij、PTij、QTij分别为线路支路上的有功功率以及无功功率、有载调压变压器支路上的有功功率以及无功功率[16]。

式（2）与式（3）表示预防控制后正常运行状态下的系统潮流方程；式（4）与式（5）表示在有载调压变压器支路中引入虚拟节点之后的电压转换方程[16]；式（6）表示预防控制后正常运行状态下区域电网传输断面的功率约束；式（7）—（13）表示预防控制中各个控制变量与状态变量的上下限约束。

1.3 预想故障状态下的静态电压稳定裕度约束

为方便说明，此处将有静态电压稳定裕度要求的正常运行状态作为预想故障状态的一个特例。预想故障下的静态电压稳定裕度约束以及区域电网间传输断面的功率约束如式（14）—（21）所示。

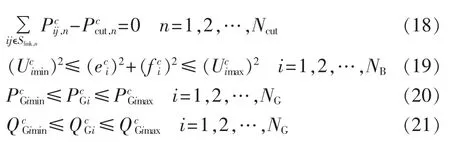
其中，各个变量的上标“c”表示该变量属于预防控制之后预想故障状态下的变量；λ为系统或者某节点负荷增长裕度的参数，通常也称为负荷裕度或者静态电压稳定裕度[4，6]，λc为系统在第 c 个预想故障下需要满足的静态电压稳定裕度期望值，可根据实际工程需要来确定。

对于静态电压稳定预防控制问题，要求预防控制后，在正常运行状态的基础上发生预想故障，在不施加新的控制措施的前提下，系统仍然具有期望的静态电压稳定裕度。即要求可调电容器注入无功、可调电抗器注入无功、有载调压变压器变比、切负荷量在预想故障状态下均保持为预防控制后正常运行状态下的值。

式（14）与式（15）为预想故障状态下系统满足静态电压稳定裕度期望值时的潮流方程；式（16）与式（17）为预想故障状态下有载调压变压器支路引入虚拟节点之后的电压转化方程；式（18）为预想故障状态下区域电网间断面的功率约束；式（19）—（21）为预想故障状态下系统节点电压幅值、发电机有功出力以及发电机无功出力的上下限约束。

如今的互联电网具有分层分区管理的特点，各个调度中心只负责维护和管理自身电网的数据。如果上述模型采用传统的集中式优化算法求解，势必会遇到基础数据的拼接问题。而且随着互联电网规模的日趋扩大，上述模型还有可能遇到收敛性问题。而现有的基于多区域的分解协调算法可以很好地解决这些问题。考虑多区域的分解协调算法需要对系统进行切分并建立相应的分解协调模型。下面将根据上述优化模型，介绍对系统的切分以及相应的分解协调模型及算法。

2 分解协调模型与分解协调内点法

2.1 互联电网的切分

本文采用母线撕裂法来对互联电网进行切分，并以如图1所示的两区域互联电网为例来说明该切分方法。

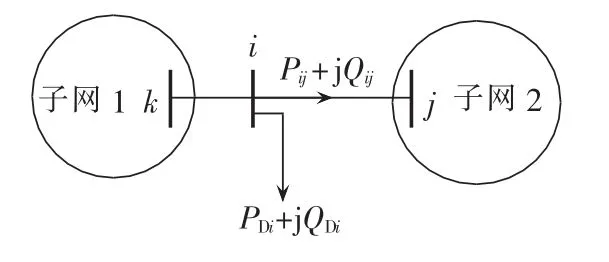
图1 两区域互联电网Fig.1 Interconnected power grid of two regional power grids

图1中，子网1和子网2通过联络线ij相连，其传输功率为Pij+jQij。其中节点i属于子网1，节点j属于子网2，而节点i又与子网1中的节点k相连，且节点i处的负荷为PDi+jQDi。

将子网1中的节点i作为边界母线，并采用母线撕裂法对边界母线进行处理，可以得到2个虚拟节点i1和i2，见图2。其中节点i1可作为子网1的边界节点，节点i2可作为子网2的边界节点。图2中，Pi1+jQi1与Pi2+jQi2分别为子网1和子网2在边界母线撕裂后所产生的注入功率；且节点i的负荷归到了子网1中，子网之间的传输断面联络线归到了子网2中。

图2 切分后的两区域互联电网Fig.2 Divided interconnected power grid of two regional power grids

由图2可知，切分后的系统要与原系统等效，节点i1与节点i2的电压实部和虚部必须分别相等，且节点i1与节点i2的注入功率要满足功率平衡条件。因此，将边界节点i1及i2的电压实部、虚部以及注入功率作为边界变量，根据第1节中所给出的优化模型，可以建立相应的分解协调模型。

2.2 分解协调优化模型

在图2所示的两区域互联电网中，子网1和子网2中除去边界节点后的内部系统变量分别用xI1、xI2来表示；而边界节点变量用xB来表示。对于子网1而言，其边界节点变量记为 xB1=（ei1，fi1，Pi1，Qi1）T；对于子网 2 而言，其边界节点变量记为 xB2=（ei2，fi2，Pi2，Qi2）T。其具体分解协调模型如式（22）—（27）所示。

式（22）表示互联电网切分后的目标函数，其具体表达式可参见式（1）；式（23）与式（24）分别表示子网1和子网2中的等式约束，对于图2所示的互联电网而言，子网1的等式约束表示形式参见式（2）—（5）以及式（14）—（17），对于子网2的等式约束表示形式可参见式（2）—（6）以及式（14）—（18）；式（25）与式（26）分别表示子网1和子网2中的不等式约束，其均可用式（7）—（13）以及式（19）—（21）来表示；而式（27）就是子网1和子网2之间的耦合关系约束，也是边界变量的协调方程，可以将其进一步表示成式（28）。

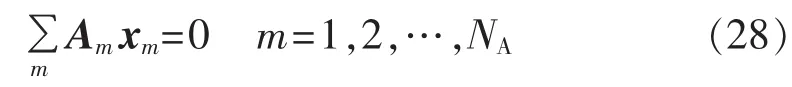
其中，NA为子网个数；Am为第m个子网与其他子网相耦合的关系矩阵；xm为第m个子网的优化变量（包括内部变量和边界变量）。

2.3 求解模型的分解协调内点法

针对如式（22）—（28）所描述的分解协调模型，本文采用文献[15]所提的分解协调内点法进行求解。其具体的求解步骤如下。

（1）设定分解协调内点法的最大迭代次数，互补间隙容许误差ε1以及库恩-图克KT（Kuhn-Tucker）条件容许误差ε2均为10-6。置当前迭代次数为K=0。给定各个优化变量以及拉格朗日乘子的初始值。

（2）计算各个子网优化模型的互补间隙（原对偶内点法中的对偶间隙）Gi以及残数（原对偶内点法迭代过程中库恩-图克方程的残差）Di。 若 G=max（G1，…，GNA）＜ε1且 D=max（D1，…，DNA，Dd）＜ε2（其中 NA为子网的个数，Dd为耦合关系约束对应的残数），则停止计算，输出最优值；否则转入步骤（3）。

（3）置K=K+1，如果K大于分解协调内点法最大迭代次数，则表示算法不收敛，停止计算；否则，转入步骤（4）。

（4）根据以下步骤更新各个子网的原变量以及对偶变量。

a.根据每个子网的目标函数、等式约束以及不等式约束对优化变量的雅可比矩阵以及海森矩阵，求解每个子网降阶后的修正方程的系数矩阵Mm及残数Bm。

b.结合各个子网边界变量的耦合关系矩阵Am，形成降阶后的修正方程中各子网耦合变量的分块系数矩阵 Em=[Am，0q×Nm]（其中 Nm为每个子网的等式约束个数，q为总的区域之间耦合关系约束的个数）。

d.计算得到Δyd之后，按照下式所示的求解各子网内部变量的解耦方程求得各个子网内部变量的增量：Mm[Δxm，Δym]T=-Bm-ETmΔyd（其中 xm、ym分别为各个子网的原变量以及等式约束的拉格朗日乘子，且在分解协调内点法中统称为各子网的内部变量；Δxm、Δym分别为其增量）。

e.根据各个子网的迭代步长以及前面所得到的优化变量的增量，对优化变量进行更新。

（5）返回步骤（2）。

3 互联电网静态电压稳定预防控制计算步骤

本文所提互联电网静态电压稳定预防控制的计算步骤如下。

a.获取互联电网的初始运行状态。

b.采用电压崩溃临界点的非线性规划算法，对每个预想故障状态下的系统静态电压稳定性进行分析。将不满足静态电压稳定裕度要求的预想故障作为关键预想故障。如果所有的预想故障都满足静态电压稳定裕度要求，则停止计算，并输出预防控制结果；否则，转入步骤c。

c.针对关键预想故障，根据第1节所述内容建立预防控制优化模型；进而根据第2节内容建立其分解协调优化模型，并采用分解协调内点法求解。

d.采用所得到的预防控制结果对初始运行状态下的互联电网控制变量进行调整，并返回到步骤b。

4 仿真分析

4.1 测试系统的基础数据

为了验证本文所提互联电网静态电压稳定预防控制模型及其算法的正确性和有效性，对如图3所示的两区域互联电网进行了仿真分析。需说明的是，该系统是由2个IEEE 118节点系统构成的236节点系统，而每个圆代表一个IEEE118节点系统。该互联电网中各节点的编号构成如下：设区域号为n，则各区域节点i对应原IEEE118系统的编号为i+（n-1）×118，各子区域中的系统数据均与原IEEE 118节点系统数据相同。其中，区域电网间断面所包括的3条联络线的支路电阻标幺值分别是0.014 5、0.016 4、0.0247，支路电抗标幺值分别是 0.0481、0.0741、0.064，支路电纳标幺值分别是0.01198、0.01972、0.062。同时，为了使该测试系统在预想故障状态或者重负荷状态下可能出现静态电压稳定问题，增加节点43和节点161的负荷为36+j14MV·A，增加节点44以及节点162的负荷为62+j31 MV·A。并根据实际工程要求，将正常运行状态下以及预想故障状态下的静态电压稳定裕度期望值 λ 取为 0.1[6]。

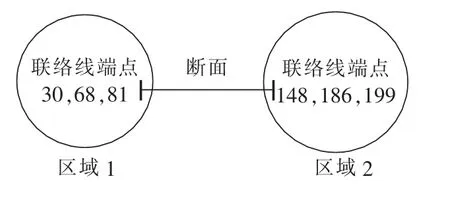
图3 IEEE 118×2测试系统Fig.3 IEEE 118×2 test system

4.2 仿真结果及分析

为了考察断面不同功率设定值给互联电网静态电压稳定预防控制结果带来的影响，本文针对以下3种情况分别进行了预防控制仿真分析：

a.预防控制后正常运行状态下以及预想故障状态下互联子网传输断面功率指定值为5 p.u.；

b.预防控制后正常运行状态下以及预想故障状态下互联子网传输断面功率指定值为4 p.u.；

c.预防控制后正常运行状态下以及预想故障状态下互联子网传输断面功率指定值为3 p.u.。

首先对上述3种仿真条件下的测试系统进行静态电压稳定性分析，可以得到其关键预想故障以及相应的静态电压稳定裕度，如表1所示。由表1可以发现，在这些关键预想故障状态下，系统的静态电压稳定裕度都小于其期望值0.1，不满足静态电压稳定裕度要求，需要实施预防控制。

表1 预防控制之前的关键预想故障及其相关信息Table 1 Critical contingencies before preventive control

根据表1所示的关键预想故障以及上述3种仿真条件，按照本文第1节与第2节所述的方法建立互联电网静态电压稳定预防控制优化模型，进而采用分解协调内点法进行求解，并在串行计算模式下进行了仿真分析。同时，为了进一步说明采用分解协调内点法求解本文优化模型的正确性和有效性，本文还针对集中式优化算法（此处采用的是预测-校正原对偶内点法）进行了对比仿真分析。2种算法中，互补间隙的容许误差均取为10-6。

仿真过程中，无论是集中式优化算法还是分解协调内点法，降阶后修正方程的求解是影响算法计算时间的重要因素，修正方程系数矩阵的维数越高，求解修正方程则越困难。表2给出了分解协调内点法与集中式优化算法中，降阶后修正方程系数矩阵的维数。由此可以看出，集中式优化算法中的修正方程系数矩阵维数远大于分解协调内点法中的修正方程系数矩阵维数，从而理论上说明了集中式优化算法求解修正方程的难度远高于分解协调内点法。此处需要说明的是，由于在3种仿真条件下，所得到的关键预想故障数目分别相同，同时又是针对同一测试系统，因此，每种仿真条件下2种优化计算方法的修正方程系数矩阵维数是分别相同的。所以，表2仅展示了其中一种仿真条件下2种计算方法的修正方程系数矩阵维数。

表2 2种计算方法下的修正方程系数矩阵维数Table 2 Dimensions of corrected equation coefficient matrix for two algorithms

在针对3种不同仿真条件进行仿真分析时发现，无论是集中式优化算法还是分解协调内点法，其预防控制过程都仅需要迭代1次就可以使得系统在正常运行状态下以及预想故障状态下满足静态电压稳定裕度要求，同时能满足区域电网间传输断面的功率约束。表3与表4分别给出了采用集中式优化算法与分解协调内点法求解预防控制优化模型所得到的结果。

表3 不同断面功率指定值下集中式优化算法的仿真结果Table 3 Simulative results of centralized optimal algorithm for different interface power settings

表4 不同断面功率指定值下分解协调内点法的仿真结果Table 4 Simulative results of decomposition-coordination interior point method for different interface power settings

从表3与表4的预防控制代价上看，采用分解协调内点法所得到的预防控制代价与集中式计算方法得到的预防控制代价一致，说明分解协调算法能达到与集中式优化算法等效的计算精度。从迭代次数上看，分解协调内点法的迭代次数比集中式优化算法的迭代次数要多，这是由系统分区之后各子区域边界变量在优化过程中需要不断交互协调而造成的。从计算时间上看，集中式优化算法比分解协调内点法的计算时间稍多一点，这是因为集中式优化算法中降阶后修正方程的矩阵维数很大，而分解协调内点法中降阶后修正方程的系数矩阵维数较之则大幅减少，从而减少了计算时间，这从表2也能体现出来。由此看出，在考虑断面功率约束的互联电网静态电压稳定预防控制中，建立分解协调优化模型并采用分解协调内点法求解是正确有效的，也是很有必要的。

另外，从表3与表4的预防控制代价中还可以看出，当断面功率指定值为5 p.u.时，所得到的预防控制代价最小；而当断面功率指定值为3 p.u.时，所得到的预防控制代价最大。这是因为在实施预防控制之前，断面传输功率就是5.0702 p.u.，所以在实施预防控制的过程中，将断面传输功率指定为5 p.u.时，对系统设备的调整就相对小一些，预防控制代价就小一些；而当断面功率指定为3 p.u.时，在实施预防控制的过程中，对系统设备的调整就相对大一些，预防控制代价也就大一些。

同时，表3与表4也给出了预防控制之后静态电压稳定裕度较小的2个预想故障及其静态电压稳定裕度。由此可以发现，经过预防控制后系统在正常运行状态下以及预想故障状态下均能满足静态电压稳定裕度要求。

以上仿真结果表明，当互联电网在正常运行状态下或者预想故障状态下出现静态电压稳定问题时，采用本文所提静态电压稳定预防控制模型及算法对互联电网实施预防控制之后，可以使系统在正常运行状态下和预想故障状态下均满足静态电压稳定裕度要求与断面功率约束要求，提高了系统的静态电压稳定裕度，证明了本文所提考虑断面功率约束的互联电网静态电压稳定预防控制模型及其算法的正确性和有效性。

5 结论

本文提出了考虑断面功率约束的互联电网静态电压稳定预防控制模型及其算法。该预防控制模型包含了正常运行状态下的可行性约束、预想故障状态下的静态电压稳定裕度约束以及区域电网间传输断面功率约束。针对互联电网分层分区管理的特点，建立了相应的分解协调优化模型，并采用分解协调内点法求解。针对测试系统的仿真分析表明了本文所建立的互联电网静态电压稳定预防控制模型既能保证系统在正常运行状态以及预想故障状态下的静态电压稳定性，也能满足系统在各个运行状态下区域电网间传输断面的功率约束，证明了本文所建立预防控制模型的正确性和有效性。通过集中式优化算法与分解协调内点法的仿真对比分析则表明了集中式优化算法在求解大型互联电网静态电压稳定预防控制优化模型时，其难度远高于分解协调内点法，说明了在大型互联电网的静态电压稳定预防控制中建立分解协调优化模型并采用分解协调内点法进行求解的正确性与必要性。因此，本文所提互联电网静态电压稳定预防控制模型及其算法能为运行调度人员监视以及控制互联电网的安全稳定运行提供决策支持。