基于SE-DEA模型的扩展黑启动方案恢复相对效率研究

王大江，顾雪平，贾京华

（1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2.河北电力调度通信中心，河北 石家庄 050021）

0 引言

大停电后快速有序的恢复是减小停电损失的有效措施，在现代电力系统规模日益扩大、结构越来越坚强，已经进入以智能化为主要特征的第三代电网的背景下[1]，各种故障仍有可能发生，自然灾害亦是电网安全稳定运行面临的威胁，灾难性事故仍无法完全避免，近期发生的多起大停电事故及其恢复过程再次提供了实例[2-3]。大停电后的恢复过程是一个复杂的控制决策问题，根据恢复过程中不同时期的任务，通常分为黑启动、网架重构和负荷恢复3个阶段，黑启动阶段是恢复的初始阶段，是后续恢复的基础和前提。

国外学者从20世纪80年代开始对恢复问题进行研究，随后国内外众多学者对黑启动问题进行了深入研究，取得了卓有成效的成果，主要包括黑启动方案制定的原则及框架[4-7]、黑启动阶段相关技术问题仿真分析[8-12]、黑启动方案优化及评估决策[13-15]；国内多数电网公司根据各自电网结构和电源分布特点制定了相应的黑启动预案及进行了部分实际黑启动试验[16-20]；文献[21]首次提出了以黑启动电源同时启动多个被启动机组的扩展黑启动恢复策略，突破了常规启动策略启动1台机组的思路限制；文献[22]进一步对考虑后续恢复影响的扩展黑启动方案进行优化决策。在黑启动阶段同时启动多台机组可为后续恢复提供更大功率支持，加快恢复进程，为大停电后的恢复提供了一种新思路，对扩展黑启动方案恢复效率评估具有重要意义，能够为优选综合效率高的恢复方案提供科学依据。

数据包络分析DEA（Data Envelopment Analysis）是一种重要的非参数生产单元相对效率测度方法，由于具有评估结果客观等众多优点而得到较广泛应用[23-26]，现有的研究中多数采用数据包络分析的基本模型，局限性是无法对有效的决策单元进一步排序。为克服该不足，专家进行了有益的改进[27-29]，文献[27-28]将数据包络分析与层次分析法相结合，充分发挥了2种方法的优点，但文献[27]在构造判断矩阵时受专家主观偏好因素制约，评估准则权重客观性相对不足，影响方案最终排序结果；文献[28]由数据包络分析计算结果构造的判断矩阵会出现元素全为1的情况而无法对方案排序；文献[29]引入最优与最差2个虚拟方案，建立改进后的数据包络分析模型，但采用改进后模型计算出的公共权重受约束条件中非阿基米德无穷小量ε取值的影响，会得出不同的排序结果。

本文提出了基于改进后的超效率数据包络分析SE-DEA（Super Efficiency DEA）模型的扩展黑启动方案恢复相对效率评估方法，首先构建了反映其恢复过程中多种要素的输入、输出指标，在此基础上采用超效率数据包络分析模型对扩展黑启动方案相对效率进行测度，最后河北南网实际电网的应用验证了所提指标的合理性和方法的有效性。

1 数据包络分析模型原理

1.1 CCR模型

数据包络分析模型是由著名运筹学家Charnes、Copper、Rhodes等在1978年提出的一种重要的效率评价方法[30]，将工程效率的概念推广到多输入多输出系统的相对效率评价中，评价依据决策单元实际的输入和输出，避免了主观因素的影响，采用数学规划原理评估决策单元的相对效率，随后得到迅速发展和广泛应用。

第一个重要的数据包络分析模型是CCR（Charnes-Copper-Rhodes）模型，假设有n个决策单元，每个决策单元Dj有m项输入和s项输出，即Xj和Yj，在满足平凡性、凸性、锥性、无效性和最小性公理体系条件下的生产可能集为：

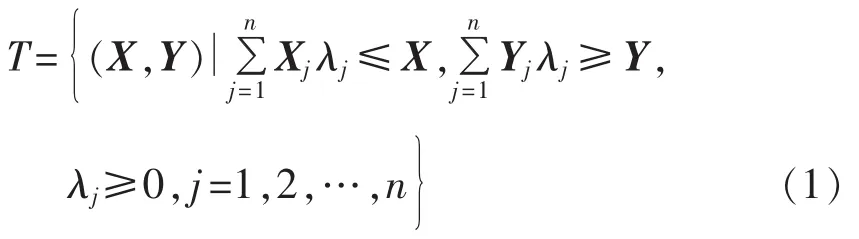
在上述生产可能集中，对于某一决策单元Dk，评价其相对效率的输入型CCR模型可用如下线性规划模型表示：

其中，θ为被评价单元Dk的相对效率值；λj为输入、输出指标的权重系数；xij和yrj分别为Dj中第i个输入量和第r个输出量；xik和yrk分别为Dk中第i个输入量和第r个输出量。

引入松弛变量s-i、s+r和非阿基米德无穷小量ε（一般取 10-6）后，模型（2）的对偶规划形式如式（3）所示。

1.2 超效率CCR模型

在利用CCR模型计算决策单元相对效率时，得到的有效决策单元效率值都为1，而有效决策单元往往不止1个，因而无法对有效的决策单元之间进一步详细地区分效率高低。为了克服基本CCR模型出现的不足，Andersen、Petersen在1993年提出了一种改进的方法，称为超效率模型，输入型超效率CCR模型可表示为：

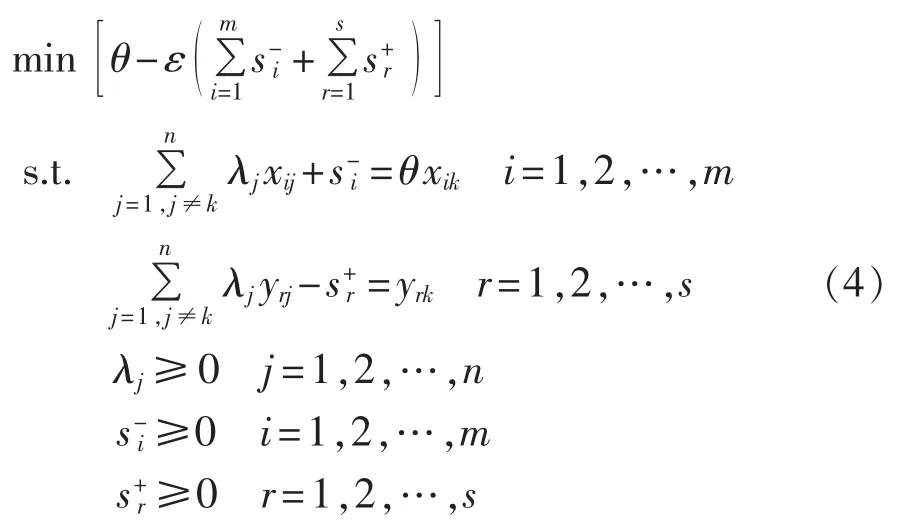
式（4）中数学变量含义与式（3）中的含义相同，对比两式可知，超效率CCR模型与基本CCR模型的区别在于被测单元Dk被从参考集内移去，Dk与其他所有决策单元的线性组合进行比较，有效决策单元效率计算结果可能超过1，故称之为超效率模型，而对于非有效决策单元，效率计算结果与基本CCR模型相同。

通过图1可直观说明该模型，图中有4个决策单元，分别为A、B、C、D，设每个决策单元有2个输入指标和 1 个输出指标，输入指标分别为（1，4）、（2，2）、（5，1.5)、（3，3），为方便起见，输出指标设为 1。 由 AB线段和BC线段组成有效前沿面，决策单元A、B、C为有效单元，D为非有效单元，A、B、C以各自为参考点，相对效率值均为1，把B从参考集中移去，新的前沿面由AC虚线所组成，B点与参考集中其他单元比较，B′成为B的新参考点，得到B的相对效率值为1.42，对A、C决策单元采用同样方法求出对其他决策单元的相对效率值分别为2和1.33，对无效决策单元D，超效率评价值不变，为0.667，则可实现对所有决策单元的排序，结果为A＞B＞C＞D。

图1 超效率CCR模型图解Fig.1 Diagram of SE-CCR model

2 扩展黑启动方案恢复相对效率评估

2.1 评估指标的构建

扩展黑启动方案的制定包含启动电源的选择、被启动机组的确定及其启动顺序优化、为被启动机组提供启动功率的充电路径的优化等问题，是一项复杂的系统优化决策问题，而采用超效率数据包络分析模型评估已制定的扩展黑启动方案恢复相对效率时，首先要建立科学合理的评估指标，在遵循制定指标的系统性、科学性、适用性等基本准则下，从黑启动方案制定的基本原则出发[23]，结合扩展黑启动恢复过程中的具体实际特点，借鉴已有的研究成果[15]，建立的评估指标如表1所示。

表1 各项评估指标Table 1 Assessment indexes

2.2 指标的定义

a.机组恢复的充电路径由相对长度较长、不同电压等级的线路所组成，由于线路对地电容产生的大量无功功率及开关的合闸操作，可能会引起工频过电压、操作过电压及黑启动电源自励磁等问题，而充电功率的大小与线路对地电容正相关，路径中经过变压器变换电压次数的增多会增加三相不同期合闸和变压器发生铁磁谐振的概率，因此可用充电路径线路电纳及电压转换次数表示路径恢复代价指标R，计算公式为:

其中，L为恢复路径中线路条数；Bl为线路l折算到同一电压等级下的线路电纳；Tc为路径中电压转换次数；α为转换系数。

b.机组启动功率指标Pcr为各台被启动机组恢复时由各种辅机组成的厂用电系统消耗的功率之和。

c.恢复总时间指标Ts是由黑启动电源经充电路径为被恢复机组提供启动功率开始到所有机组全部启动成功后并网经历的时间。

d.黑启动阶段恢复的机组容量越大、机组升负荷率越大，能够为后续恢复以更短的时间提供更多功率支持，重要负荷周围的机组启动同样有利于后续恢复，因此机组恢复效果指标从机组特性、对后续恢复的影响等方面考虑，将其定义为：

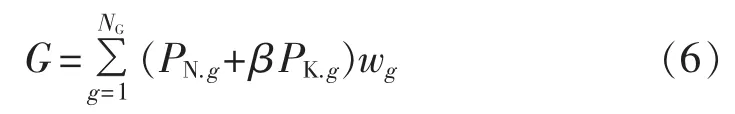
其中，NG为恢复的机组数；PN.g为机组g的额定功率；PK.g为机组g的升负荷率；β为转换系数；wg为机组g的优先级，由其周围的负荷重要程度决定。

e.黑启动阶段形成的局部小网络是后续恢复的基础，不同方案形成的小网络拓扑位置不完全相同，定义网络重要度指标反映局部小网络的重要程度，从网络拓扑连通性角度计算该指标。设恢复的小网络中节点数为N，wij为节点i与j之间直接相连线路的权值（本文取折算到同一电压等级下的电抗），与节点i直接相连的线路个数为Ni，lih为节点i到节点h间最短路径的权值，将节点i的重要度定义为：

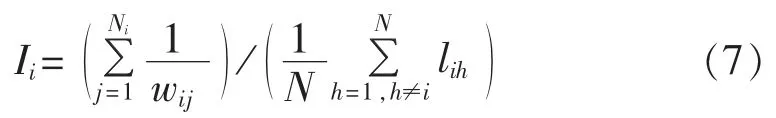
则局部小网络的网络重要度为：

2.3 扩展黑启动方案相对效率评估步骤

综合上述超效率数据包络分析模型和评估指标，扩展黑启动方案恢复相对效率评估步骤如下：

a.建立适用于方案相对效率评估的指标；

b.确定多个可行的待评估扩展黑启动方案；

c.根据各方案恢复的局部小网络及机组参数，计算得到评估指标；

d.以超效率数据包络分析模型对每一个待评估方案建立规划方程，并求解得到各方案的恢复相对效率。

3 算例分析

3.1 算例描述

将上述评估方法应用于河北南网实际电网中，以其扩展黑启动方案作为研究实例，河北南网以张河湾抽水蓄能电站为启动电源，其装机容量为4×250 MW，通过技术校验合格可行的2套扩展黑启动方案恢复形成的局部网络如图2所示，分别以KD1、KD2表示其方案号，转换系数α取0.5，β取1。

图2 河北南网扩展黑启动方案的网络结构Fig.2 Network structure of extended black-start restoration plans for Hebei Southern Grid

启动1台机组的常规黑启动策略作为扩展黑启动策略的一种特例，为了比较2种恢复方式效率的差异性，将常规黑启动方案纳入评估方案集中，常规黑启动方案如表2所示。

表2 常规黑启动方案列表Table 2 Conventional black-start plans

根据河北南网电网的实际数据，通过计算分析得到各方案的输入、输出指标值，如表3所示。

表3 各恢复方案的输入、输出指标值Table 3 Value of input and output indexes for different restoration plans

3.2 计算结果

按照上述超效率数据包络分析CCR模型（4），以表3中的输入、输出指标数据分别对各个待评估方案建立评估模型，以方案KD1为例，具体模型如式（9）所示。

利用数学规划软件求解得到方案KD1相对效率θ=1.5，求解所有评估方案的规划模型得到各自相对效率，如表4所示。各方案基本CCR模型效率计算结果见表4中第2列，采用文献[29]中改进数据包络分析模型在ε分别取0.0001和0.00004时的计算结果见表4中第4、5列。

表4 各恢复方案的相对效率评估结果Table 4 Relative efficiency evaluated by different methods for different restoration plans

从表4可以看出，基本CCR模型计算结果中有多个相对效率值为1的有效方案而无法对有效方案进一步排序，对于有效的方案，可根据其超效率模型评价值进一步区分优劣；文献[29]中改进数据包络分析模型也可对有效方案进一步排序，但计算出的方案效率值受ε取值的影响，ε取不同值时，同一方案效率值不同，方案排序结果不同。因此，超效率数据包络分析模型评价值更具客观性和参考性，具有更大应用优势。

在算例中，方案KD1启动5台机组，启动机组数最多，形成的局部小网络规模较其他方案大，其路径指标、启动功率指标相对最大，但其机组恢复效果、网络重要度指标最好，故其相对效率最高；方案KD2启动4台机组，其相对效率次之；扩展黑启动方案KD1、KD2的恢复相对效率均高于常规黑启动方案D1—D5的恢复相对效率。通过分析可知评估结果与实际相符合、客观合理，扩展黑启动是对常规黑启动的合理有效扩展。

4 结论

本文结合黑启动方案制定的基本原则与扩展黑启动恢复过程的具体实际问题，建立了适用于扩展黑启动方案相对效率评估的输入、输出指标，采用超效率数据包络分析模型对扩展黑启动方案恢复相对效率进行评估，评估结果客观合理，可为恢复方案制定决策提供多角度的参考依据，河北南网扩展黑启动方案的实例计算结果验证了所提指标的合理性和评估方法的有效性，该方法理论清晰，结果直观，同样可为电力系统中其他方面的效率评估问题提供参考。