利用基波电流相量变化率识别行波保护中雷击干扰

刘兴茂，林 圣，李小鹏，何正友

（西南交通大学 电气工程学院，四川 成都 610031）

0 引言

超／特高压输电线的继电保护快速、可靠地切除线路故障能有效保证电网的暂态稳定并提高输电线的传输容量[1]。与基于工频量的传统保护相比，利用暂态量构成判据的行波保护具有超高速动作的优点，且不受系统振荡、线路分布电容、电流互感器饱和等因素的影响[2-4]。然而，行波保护原理仅仅根据装置检测的高频暂态行波的特征识别区内外故障，并不区分该暂态行波是由短路故障产生还是由其他因素引起。所以，行波保护原理难以正确区分故障产生的高频行波与雷击输电线引起的高频干扰信号，造成行波保护的可靠性不足，影响行波保护在输电线中的实际应用。因此，快速、准确识别雷击干扰对于提高行波保护的可靠性以及促进行波保护实用化具有重要意义。

通过众多学者的深入研究，多种抗雷击干扰的方法相继被提出。文献[5-7]选取不同的信号处理工具分解暂态电流信号，利用高、低频段分量的能量比构成判据，但是仅依据能量比不易区分弱故障性雷击与非故障性雷击。文献[8]综合利用电流故障分量的能量分布差异和波形特征进行雷击干扰识别，由于对端母线的反射作用导致由非故障性雷击产生的雷电波具有截波的特征，该方法会将发生在线路末端的非故障性雷击误判成故障性雷击。文献[9]依据暂态电压的线模和零模信息构成判据可以正确区分感应雷击与短路故障，但该判据不能识别直击雷产生的雷击干扰。文献[10]提出“波形一致性系数”的概念并以此进行雷击干扰识别，但影响该系数大小的因素有待进行理论分析，以便为门槛值的整定提供依据。

本文在分析短路和雷击产生的附加电流分量特征的基础上，研究了附加电流分量对基波电流相量变化率的影响，由此提出利用基波电流相量变化率识别雷击干扰的方法。仿真结果表明本方法能可靠识别雷击干扰。

1 雷电波及雷击线路情况分析

1.1 雷电波的波形

雷云放电时形成雷电波，包括雷电流和雷电压，受气候、自然条件等因素影响，雷电波的幅值、波前时间和半峰值时间皆为随机变量。实测表明，对于中等强度以上的雷电波，其波前时间T1在1～5 μs范围内，半峰值时间 T2在 20～100 μs范围内[11-12]。 国际电工委员会（IEC）采用T1／T2表示雷电波的波形，图1所示即为 1.2／50 μs雷电流波形。

图1 1.2／50 μs雷电流波形Fig.1 Waveform of 1.2 ／50 μs lightning current

雷电波为单极性脉冲波，可用双指数函数将雷电波等值为标准波形[11]。雷电流的表达式为：

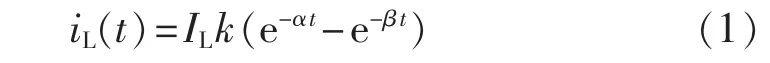
其中，IL为雷电流幅值；k为波形校正系数；α、β分别为波前、波尾衰减系数。k、α、β的值可依据雷电流的波前时间T1和半峰值时间T2确定。

1.2 雷击线路情况分析

雷击线路附近地面时，输电线路会产生感应雷过电压。由于雷击不直接作用于线路，感应雷过电压幅值较小，不会引起具有较高绝缘水平的超高压输电线路发生短路故障[13]。雷击塔顶及塔顶附近避雷线、档距中央的避雷线或绕击导线会在输电线上产生直击雷过电压。直击雷过电压幅值超过一定水平将引起线路绝缘子串的闪络，由图2所示绝缘子串伏-秒特性曲线可知[14-15]：当雷电波电压幅值增大，引发绝缘子串发生闪络时，闪络可能发生在波前、波峰或波尾，分别如图2中点a、b、c所示；闪络发生后，雷电波被截断，导致雷电波突然跌落至零，如图2中实线1所示。理想情况下，被截断的雷电压表达式为：

其中，tc为雷电压被截断时刻。

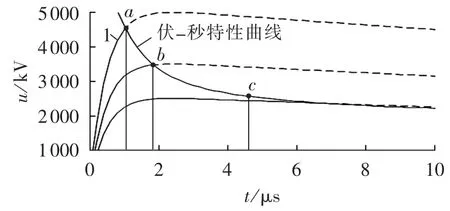
图2 绝缘子串伏-秒特性曲线Fig.2 Voltage-time curve for insulators

雷击闪络转化为稳定的工频电弧导致线路发生瞬时性短路故障，此时保护应立即动作以避免线路绝缘损坏形成永久性故障。因此，依据雷击是否造成线路发生短路故障可将雷击分为非故障性雷击和故障性雷击2类。对于故障性雷击，保护应迅速跳闸；对于非故障性雷击，保护应可靠不动作。

2 故障与雷击情况下的特征分析

2.1 故障与雷击的附加电流分量

根据叠加原理，输电线发生短路故障、遭受故障性雷击或非故障性雷击可将系统视为正常运行状态与附加状态的叠加。因此，输电线电流的表达式为：

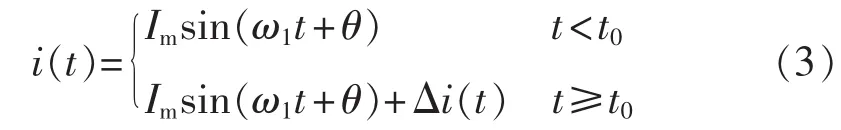
其中，t0为短路故障、故障性雷击或非故障性雷击的起始时刻；Im、ω1、θ分别为基波电流幅值、角频率和初相角；Δi（t）为附加电流分量。

线路发生短路故障，式（3）中附加电流分量 Δi（t）即为故障分量ΔiF（t），包含衰减非周期分量、基波故障分量及各次高频谐波，其波形图如图3（a）所示。Δi（t）的表达式为：

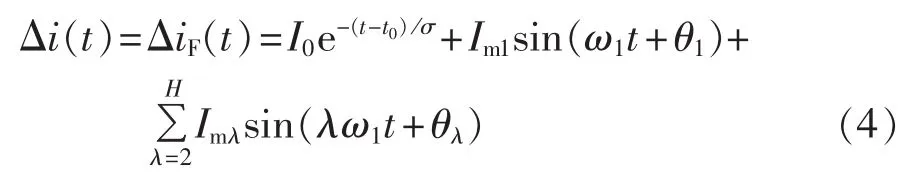
其中，I0、σ分别为非周期分量电流初始值和衰减时间常数；ω1为基波的角频率；Im1、θ1分别为基波电流故障分量幅值和初相角；λ为谐波次数，Imλ、θλ分别为各次谐波幅值和初相角；H为最高谐波次数。

线路遭受故障性雷击，式（3）中附加电流分量Δi（t）包含雷击所产生的雷电波和短路故障所产生的故障分量 ΔiF（t），其波形如图3（b）所示。 Δi（t）表示为：

其中，τf为雷击时刻与故障初始时刻的时间间隔；iG1、iG2、iG3分别为式（2）表达的被截断的雷电压所产生的第1、2、3次到达母线的雷电波；τ1、τ2、τ3分别为雷电波第1、2、3次到达母线的时间延迟。

线路遭受非故障性雷击，式（3）中附加电流分量Δi（t）为雷击所产生的雷电波，其波形如图3（c）所示。 Δi（t）可表示为：

其中，iL1、iL2、iL3为式（1）表达的雷电流分别经避雷器放电、母线的折射和反射作用后形成的雷电波。

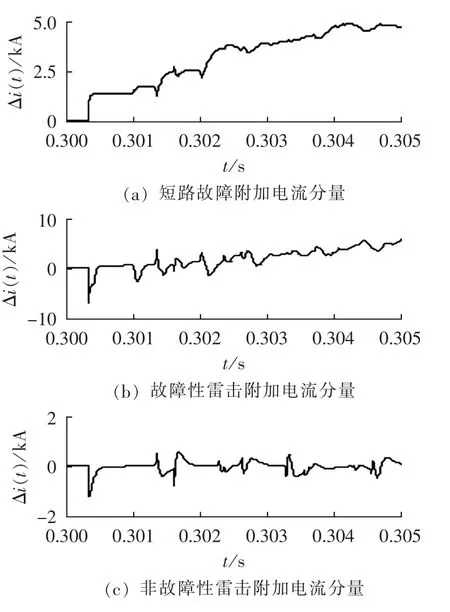
图3 附加电流分量Fig.3 Additional current component

2.2 故障与雷击情况下的基波电流相量变化率

输电线路发生短路故障或遭受雷击后，受附加电流分量的作用，测量的实际基波电流会不同程度地偏离正常状态基波电流分量。定义测量的实际基波电流相量和正常状态基波电流相量之差的幅值与额定电流的比值为基波电流相量变化率。计算基波电流相量变化率的算法步骤如下。

a.通过时频分析确定输电线发生短路故障或遭受雷击的起始时刻t0。

b.设基波电流周期为T，取t0-T至t0这段时间的电流信号，利用快速傅里叶变换（FFT）计算出系统正常运行状态的基波电流相量Ip。

c.针对 t0之后的时刻 t1，依据式（7）计算 t1时刻系统正常运行状态下的基波电流相量估计值Ie：

d.取t1-T至t1这段时间的电流信号，利用FFT计算t1时刻实际基波电流相量If。

e.计算t1时刻的基波电流相量变化率为：

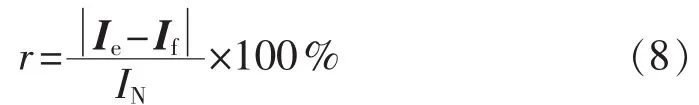
其中，IN为电流额定值。

由式（4）、式（5）可知，线路发生短路故障或遭受故障性雷击，附加电流分量中都包含故障所产生的衰减非周期分量和基波故障分量，在这2个分量的作用下，上述算法中实际基波电流相量If与估算的基波电流相量Ie的差值会在短时间内迅速增大。图4（a）中曲线1、曲线2分别为某给定系统线路中点发生短路故障和遭受故障性雷击后基波电流相量变化率随时间变化曲线。短路和故障性雷击初始时刻均为0.3 s，5 ms后2种情况下的基波电流相量变化率都超过了50%。

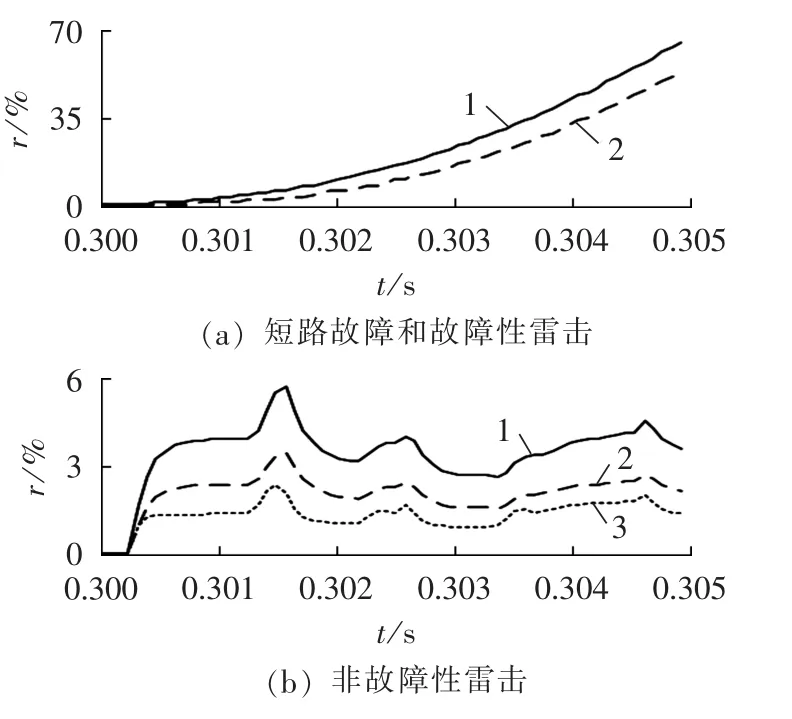
图4 基波电流相量变化率Fig.4 Change rate of fundamental current phasor

与短路故障及故障性雷击不同，线路遭受非故障性雷击后，附加电流分量仅包含雷击所产生的雷电波。为了分析雷电波对基波电流相量变化率的影响，给出了某给定系统线路中点遭受非故障性雷击后基波电流相量变化率随时间变化曲线，如图4（b）所示。其中，曲线 1是波形为 5／100 μs、幅值为 5 kA 的雷电流作用于线路的结果；曲线2是波形为5／100 μs、幅值为3 kA的雷电流作用于线路的结果；曲线3是波形为1.2／50 μs、幅值为5 kA的雷电流作用于线路的结果。非故障性雷击初始时刻为0.3 s，在5 ms内所有基波电流相量变化率都不超过6%，远低于短路故障或故障性雷击后所得结果。同时，图4（b）反映出线路遭受非故障性雷击后基波电流相量变化率的大小受雷电流波形及幅值的影响，雷电流半峰值时间越长、幅值越高，非故障性雷击后的基波电流相量变化率就越大。

由上述分析可知，利用基波电流相量变化率可识别非故障性雷击所带来的雷击干扰，从而保证输电线路发生短路故障或遭受故障性雷击时继电保护可靠动作，线路遭受非故障性雷击时继电保护可靠不动作。

3 雷击干扰与故障的识别算法

3.1 利用S变换定位雷击或短路故障的起始时刻

S变换（S transform）是一种时频分析方法，由R.G.Stockwell于 1996 年提出[16-17]。 作为短时傅里叶变换和连续小波变换的扩展，S变换具有短时傅里叶变换单频率独立分析及小波变换多频率分析的优点[18]。在S变换中，高斯窗函数是随频率升高而收缩的窗函数，这使得S变换具有良好的时频分辨特性。利用S变换可提取信号中的单频率信号分量，还能获得单频率信号分量的幅值随时间变化的分布。因此，本文利用S变换确定雷击或短路的起始时刻，下面给出具体步骤。

a.获取附加电流分量 Δi（t），图5（a）给出了某给定系统线路遭受非故障性雷击后A相电流的附加电流分量。

b.在频率f1上对附加电流分量Δi（t）进行离散S变换，变换结果为一维复相量，其表达式为：

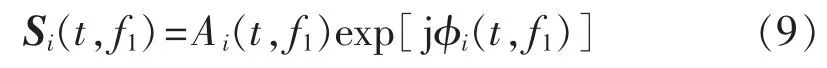
图5 附加电流分量及其经S变换后的幅值Fig.5 Additional current component and its S transform

其中，Si（t，f1）为频率为 f1的行波，Ai（t，f1）为该行波的幅值（如图5（b）所示），φi（t，f1）为该行波的相位。

c.根据 Ai（t，f1）中初始行波极大值所对应的时刻tp确定雷击或短路的起始时刻为t0=tp-τ，其中τ为常数，考虑雷电流波前时间在1～5 μs范围内，τ的取值为 10 μs。

3.2 雷击干扰识别算法

根据上述分析，本文所提雷击干扰识别算法流程如图6所示，算法相关说明如下。

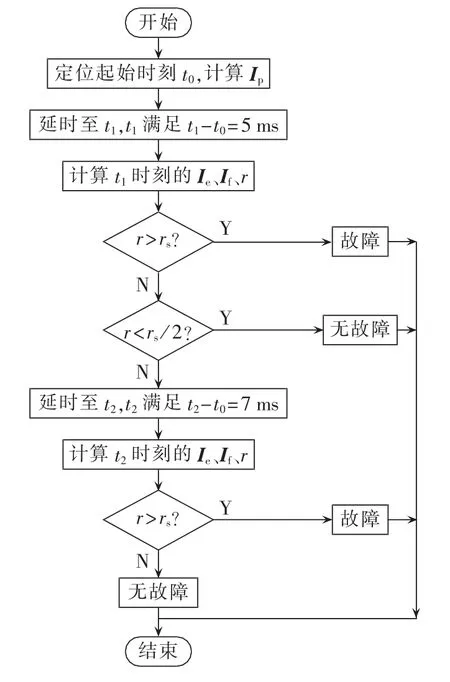
图6 雷击干扰识别的算法流程图Fig.6 Flowchart of lightning disturbance identification

a.算法利用S变换定位雷击或短路故障的起始时刻t0，取t0之前一个周期电流采样值计算系统正常运行状态的基波电流相量Ip。延时至t1时刻，依据基波电流相量变化率的算法计算出t1时刻基波电流相量估计值Ie、实际基波电流相量If以及基波电流相量变化率r。将基波电流相量变化率r与整定值rs进行比较，r大于rs时线路发生故障，r小于rs／2时线路遭受非故障性雷击。

b.如果线路发生绝缘闪络，且电流基波幅值变化量较小，则算法获得的基波电流相量变化率随时间变化较慢。因此，算法延时至t2时刻，计算出t2时刻的Ie、If和r，如果r大于 rs则线路发生故障，否则线路遭受非故障性雷击。

c.由2.2节分析可知，选取雷电流的幅值使得线路绝缘子电压达到临界闪络电压，并取雷电流波形为5／100 μs，就能获得非故障性雷击后基波电流相量变化率最大值。因此，整定值rs的设定依据为：

其中，k为可靠系数；rmax为非故障性雷击时基波电流相量变化率的最大值。

4 仿真验证

利用电磁暂态程序PSCAD／EMTDC建立如图7所示的500 kV超高压输电系统的仿真模型。输电线都采用频率相关模型；母线对地杂散电容设为Cs=0.01 μF；避雷器（MOA）采用 IEEE 推荐的频率相关模型[19]；R1为行波保护装置。系统采样频率为200 kHz，S变换选取的频率为50 kHz。依据非故障性雷击时基波电流相量变化率的最大值rmax及可靠系数k，将整定值rs设为10%。

图7 超高压输电系统Fig.7 EHV power transmission system

为了考察故障初始角较小时3.1节的方法能否准确定位故障时刻，取故障初相角为5°，仿真线路L1上与R1相距190 km处发生A相接地故障。将电流叠加噪声，信噪比为50 dB，得A相故障附加电流分量如图8（a）所示，S变换提取的50 kHz行波分量如图8（b）所示。图8（b）表明：即使故障初始角较小，应用S变换也能准确定位故障时刻。作为对比，图8（c）给出了由小波变换提取的行波，小波变换的尺度2对应 50～100 kHz。图8（c）表明，由小波变换也可定位故障时刻，与S变换不同的是，小波变换提取的行波分量频带较宽，易受高频噪声影响。

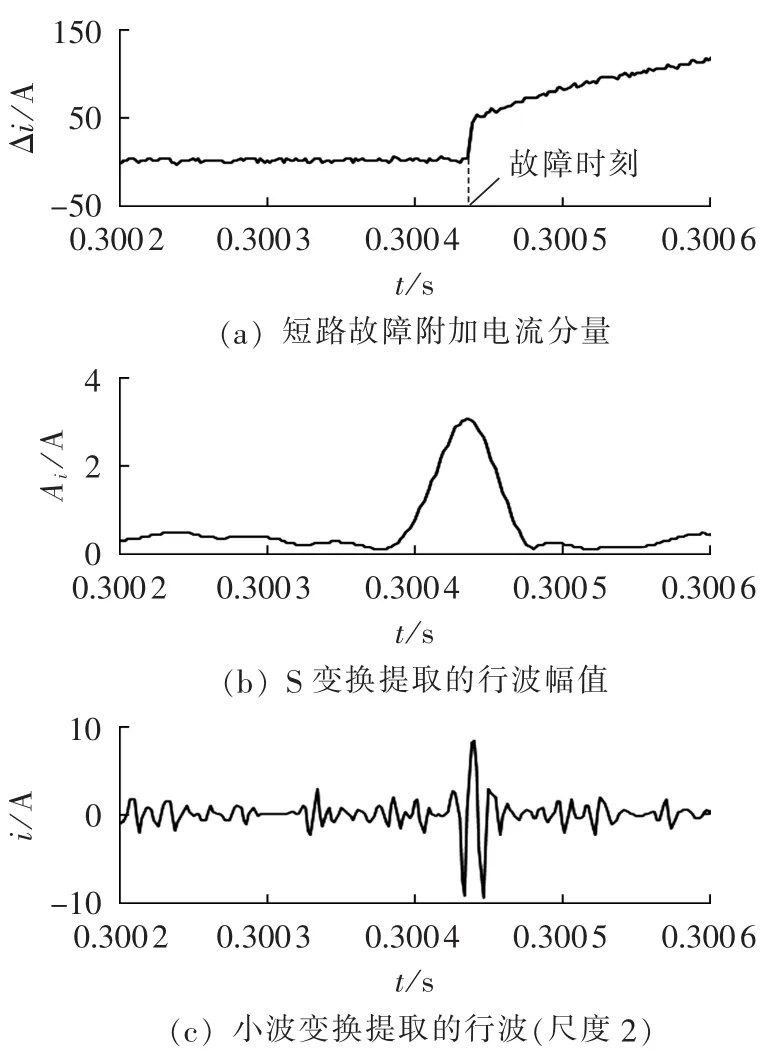
图8 A相接地故障时方法抗噪声性能Fig.8 Anti-noise performance of proposed method for phase-A grounding fault

4.1 短路故障

表1是不同工况下线路L1发生故障后，保护装置R1计算的故障后5 ms的基波电流相量变化率。表中，δ为系统电源u1与u2的相位差；rAG、rBC分别为A相接地、BC相短路时的基波电流相量变化率；Rf为过渡电阻；d为故障点和R1的距离。表1数据表明：输电线在不同故障条件下的基波电流相量变化率都大于整定值rs，行波装置能够判断出线路发生故障；短路故障后基波电流相量变化率随故障类型、故障距离、故障初相角以及过渡电阻的不同而发生变化。当线路末端发生初相角小且过渡电阻大的单相接地故障时，所得到的基波电流相量变化率较小，该值可作为设定整定值rs的校验依据。

表1 不同短路故障条件下基波电流相量变化率Table 1 Change rate of fundamental current phasor for different short circuit faults

为了分析线路短路故障时算法抗噪声的性能，取故障初相角为5°、故障过渡电阻为100 Ω，仿真线路L1上与R1相距195 km处发生A相接地故障，故障后5 ms内基波电流相量变化率如图9中的实线所示。将电流叠加噪声，信噪比为30 dB，可得故障后5 ms内基波电流相量变化率如图9中的虚线所示。图9中2条曲线的变化情况表明：在线路短路故障条件下，算法受噪声影响小，噪声干扰不会影响行波装置可靠判断线路发生故障。

图9 发生过渡电阻为100 Ω的A相接地故障时方法抗噪声性能Fig.9 Anti-noise performance of proposed method for phase-A grounding fault with 100 Ω transition resistance

4.2 故障性雷击

在线路L1上与R1相距100 km、190 km处设置不同工况的故障性雷击，取故障相电流信号计算雷击后5 ms的基波电流相量变化率，仿真结果如表2所示。幅值为20 kA的雷电流作用于线路时，雷击后10 μs引起线路短路；幅值为50 kA的雷电流作用于线路时，雷击后5 μs引起线路短路。为了分析算法在故障性雷击条件下的抗噪声性能，同时将故障电流信号以30 dB的信噪比叠加噪声后计算基波电流相量变化率。表2数据表明：故障性雷击后5 ms的基波电流相量变化率都大于整定值rs，行波装置能够判断出线路发生故障。线路遭受故障性雷击，雷电流波形被短路故障截断后在线路上形成高频率的雷电波，基波电流相量变化率的大小受雷电流波形、幅值等因素影响小，主要取决于故障位置及故障时刻。

表2 故障性雷击时基波电流相量变化率Table 2 Change rate of fundamental current phasor for lightning-strike fault

如果线路发生绝缘闪络，且基波故障分量较小，则算法获得的基波电流相量变化率随时间变化较慢。仿真线路L1上与R1相距190 km处A相受故障性雷击，故障时刻为0.3 s，且故障后基波故障分量幅值较小，仿真结果如图10所示。图10（a）给出了A相电流曲线，图10（b）给出了故障后基波电流相量变化率随时间变化曲线，由图10可知算法能够在故障后0.7 ms可靠判断线路发生了故障。

图10 基波故障分量较小时基波电流相量变化率曲线Fig.10 Curve of fundamental current phasor change rate when fundamental fault component is small

4.3 非故障性雷击

线路遭受非故障性雷击后基波电流相量变化率的大小受雷电流波形及幅值的影响。由于整定值rs是依据非故障性雷击时基波电流相量变化率的最大值设定，因此，线路遭受非故障性雷击后，行波装置能够判断出线路未发生故障。仿真线路L1上与R1相距100 km处遭受非故障性雷击，雷电流波形为5／100 μs、幅值为 10 kA，雷击后 5 ms内的基波电流相量变化率如图11中实线所示。将电流信号按30 dB的信噪比叠加噪声，所得基波电流相量变化率如图11中虚线所示。比较图11中2条曲线变化情况可知：非故障性雷击条件下，算法受噪声影响小，行波装置能可靠识别雷击干扰。

图11 非故障性雷击时基波电流相量变化率曲线Fig.11 Curve of fundamental current phasor change rate when lightning disturbance does not result in a fault

5 结论

a.线路发生短路故障或遭受故障性雷击，附加电流分量中包含衰减周期分量以及基波故障分量，导致基波电流相量变化率大幅度变化；线路遭受非故障性雷击，附加电流分量仅包含高频雷电波，雷击后一段时间内基波电流相量变化率较小。利用短路故障、故障性雷击或非故障性雷击后的基波电流相量变化率能可靠识别雷击干扰。

b.行波算法需要2 ms左右数据窗，判据的结果传输到对端装置需要2～3 ms的时间延迟，故行波原理构成的纵联保护动作时间为5 ms左右。文中所提算法能在线路发生短路故障、遭受故障性雷击或非故障性雷击后5 ms识别出雷击干扰，在保护动作前进行雷击干扰识别，不会延迟行波保护动作时间。

c.算法采用基波电流相量变化率构成雷击干扰识别判据，充分利用了基波所包含的故障信息。将该算法作为行波保护的雷击干扰判据，可使行波保护同时利用高频行波和基波所包含的故障信息，能提高保护的可靠性。