离心机闭合误差对陀螺加速度计输入量的影响

任顺清，王世明

(哈尔滨工业大学 空间控制与惯性技术中心，150080哈尔滨)

在应用离心机对陀螺加速度计进行标定时，为克服离心机一些误差的影响，对于陀螺加速度计输出的采样以及离心机主轴的转速采样都采用整周采样方式，即在满足陀螺加速度计进动整周或离心机主轴旋转整周的情况下获得相应的输出值［1-3］.加速度计［4-7］、陀螺仪［8］及由他们组成的惯性系统［9］一般在三轴转台、精密离心机等测试设备上进行标定与测试，测试设备及其数据采集系统的误差［6，8，10］均对标定误差有影响.本文将针对陀螺加速度计在离心机上标定时闭合误差对标定精度的影响进行分析.

试验时的理想条件是陀螺加速度计进动整周M的时间与离心机旋转整周N的时间相一致，从而避免由于非整周情况所产生的陀螺加速度计附加的输入比力，但是这种条件往往是很难达到的.将这种测试过程中旋转角度非整周，不能闭合的角度定义为“闭合误差”.目前采用的测试方法是以陀螺加速度计进动整周的时间作为基准，再去获得相应的离心机主轴的回转角位置，选择终止时刻的角位置与初始时刻角位置之差最小的情况确定始末时刻;但是，往往最小的角位置误差都大于10°，即闭合误差大于10°，因此分析闭合误差对于陀螺加速度计输入量的影响就显得非常有意义，因为陀螺加速度计对比力和角速率都敏感，这里的输入量包括输入比力和输入角速度.目前尚未有文献对于闭合误差如何影响陀螺加速度计输入量进行分析.本文结合带反转平台的离心机标定陀螺加速度计试验，针对可能通过闭合误差影响离心机提供给陀螺加速度计输入轴的输入比力及输入角速度的离心机各轴系间的位姿误差、角速度误差、地球自转角速度等误差项进行分析，将给出各误差项对于输入比力作用的表达式及误差大小，以及闭合误差的允差，以满足输入比力的相对误差小于10-6的要求.

带反转平台的大臂式离心机的基本结构如图1所示，相关坐标系如图2所示.由图1可知，试验时，离心机作用于陀螺加速度计输入轴方向的加速度标称值大小为为离心机的工作半径标称值，ω0为离心机的主轴角速度．令ωt表示主轴旋转的角度，γ表示方位轴旋转的角度．试验中需要根据具体的陀螺加速度计离心机测试方法选择方位轴是与主轴同步反转，还是锁定于某角位置随大臂转动这两种测试方法．

图1 精密离心机结构示意

图2 精密离心机相关坐标系

图2中，坐标系o0x0y0z0为地理坐标系，o1tx1ty1tz1t为主轴轴套坐标系，o1x1y1z1为主轴坐标系，o2tx2ty2tz2t为水平轴轴套坐标系，o2x2y2z2为水平轴坐标系，o3tx3ty3tz3t为方位轴轴套坐标系，o3x3y3z3为方位轴坐标系，o4x4y4z4为工作基面坐标系，o5x5y5z5为加速度计坐标系．文中后面提到的相关离心机误差的下标与这里各坐标的下标是相对应的．针对两种测试方法，分析离心机自身误差加上闭合误差对于陀螺加速度计输入比力的影响.

1 离心机自身误差对输入比力的影响

1.1 反转平台不旋转情况

反转平台锁定于零位，即γ=0，此时可能通过闭合误差对输入比力产生影响的离心机误差项有主轴轴套的安装误差角Δθx1t、Δθy1t，主轴径向回转 误差Δx1(ωt)、Δy1(ωt)，轴向回 误差Δz1(ωt)，主轴倾角回转误差Δθx1(ωt)、Δθy1(ωt)，水平轴与主轴的相交度Δy2t，半径误差ΔR．

考虑各项误差，相邻坐标系的齐次变换表达式如下:

主轴轴套坐标系，

主轴坐标系，

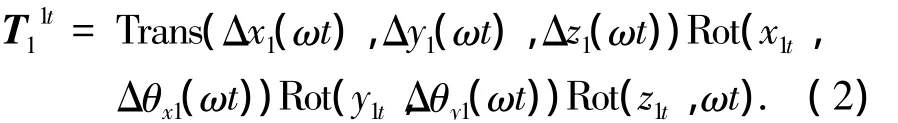
水平轴轴套坐标系，

加速度计坐标系相对于地理坐标系的齐次变换表达式为

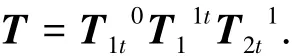
其中:Δθx1t、Δθy1t、Δy2t为常值误 差;Δθx1(ωt)、Δθy1(ωt)、Δx1(ωt)、Δy1(ωt)、Δz1(ωt)为轴系的回转误差项．根据回转误差的相关理论，回转误差主要表现为二次谐波项，相应的表达式为

省去中间的推导过程，忽略高阶无穷小量，输入比力表达式为(包含重力加速度投影和向心加速度投影)

则考虑闭合误差，即存在非整周积分的情况下，平均输入比力的误差为其中T为理想周期时间值，Δt为实际整周与理想整周的时间差值．

根据式(4)，结合各误差项的测试数据，可以给出各误差项对于输入比力在反转平台无旋转情况下的影响大小，这里设半径为2.5 m的离心机提供10 g的加速度大小，则ω为6.26 rad/s，相应的旋转一周所用的时间T为1.003 5 s.闭合误差按照10°情况计算.表1、2给出了反转平台无旋转情况下的计算结果.

表1 反转平台无旋转下离心机角度误差对加速度计输入比力的影响

表2 反转平台无旋转下离心机位移量误差对加速度计输入比力的影响

由表1和表2可知，反转平台锁定，各误差项在闭合误差影响下对于输入比力的误差影响相对较小，最大的影响为主轴径向回转误差Δx1(ωt)余弦项引起的-8.651×10-7g的输入比力误差，综合上面所有的误差项产生的输入比力误差，可以得出总的输入比力误差为-1.215×10-6g，超过了10-6g的精度要求，因此需要补偿掉综合误差.

图3给出了反转平台锁定时闭合误差与其通过离心机自身误差作用下产生的总输入比力误差之间的关系曲线，可以看出输入比力误差随着闭合误差的增加而增大，当闭合误差小于8.5°时，产生的总输入比力误差小于1×10-6g.受测试设备及整周圈数选取的限制，通常将闭合误差放宽到10°，进而通过补偿掉该项误差以满足精度要求.

综上，闭合误差为10°时，通过ω相关的离心机误差项作用产生的总的输入比力误差项较大，需进行补偿.

1.2 反转平台同步反转情况

反转平台旋转时，在γ=-ωt情况下，此时与ωt正余弦相关的离心机误差项除了式(1)～(3)涉及的误差外，还包括:方位轴径向回转误差Δx3(γ)、Δy3(γ)，轴向窜动Δz3(γ)以及倾角回转误差 Δθx3(γ)、Δθy3(γ)，相应的齐次变换式在方位轴坐标系下为

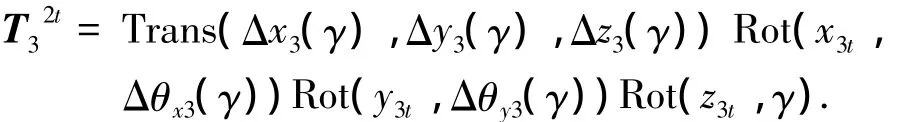
加速度计坐标系相对于地理坐标系的关系为

图3 反转平台无旋转情况下总输入比力误差与闭合误差关系

上述新加入误差同样主要表现为二次谐波项，相应的表达式为

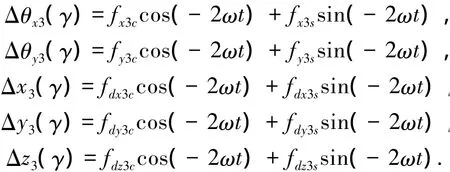
忽略中间的推导过程及高阶无穷小量，包含重力加速度投影和向心加速度投影，则此时输入比力表达式为

进而考虑闭合误差影响下的平均输入比力误差，方法同式(4).

应用同样数据计算各误差项对于输入比力在反转平台反转情况下的影响大小，其中Δy2t=0．25 mm时，Δ=2.414×10-6g，其他各误差项对加速度计输入比力的影响见表3、4.

表3和表4给出了在反转平台反转时，各误差项在闭合误差作用下对于输入比力误差的影响.其中，水平轴轴线与主轴轴线的相交度Δy2t和方位轴径向回转误差Δx3(γ)余弦项幅值fdx3c对输入比力误差的贡献最大，均为10-6g的量级．则10°闭合误差影响下总的输入比力误差为1.367×10-6g，超过了10-6的精度要求，因此需要补偿掉综合误差．

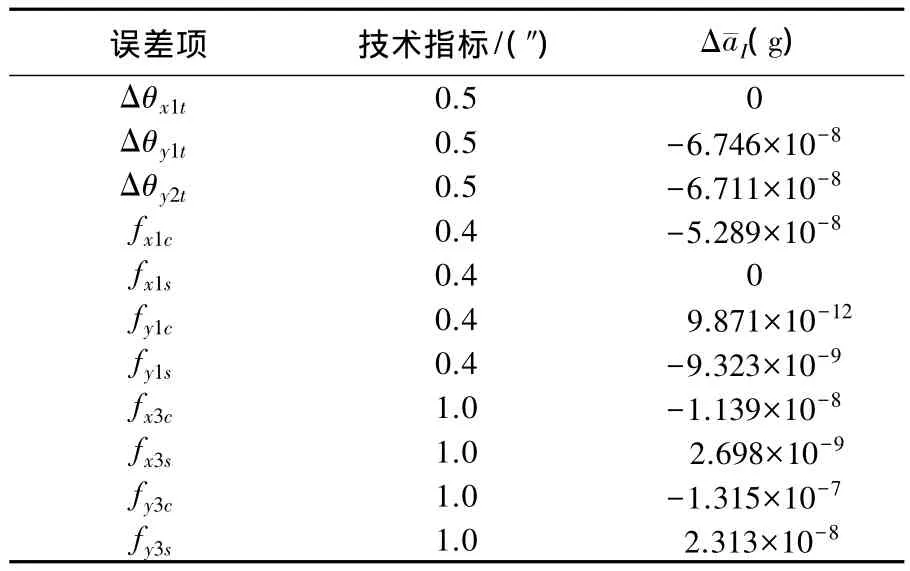
表3 反转平台反转时离心机角度误差对加速度计输入比力影响

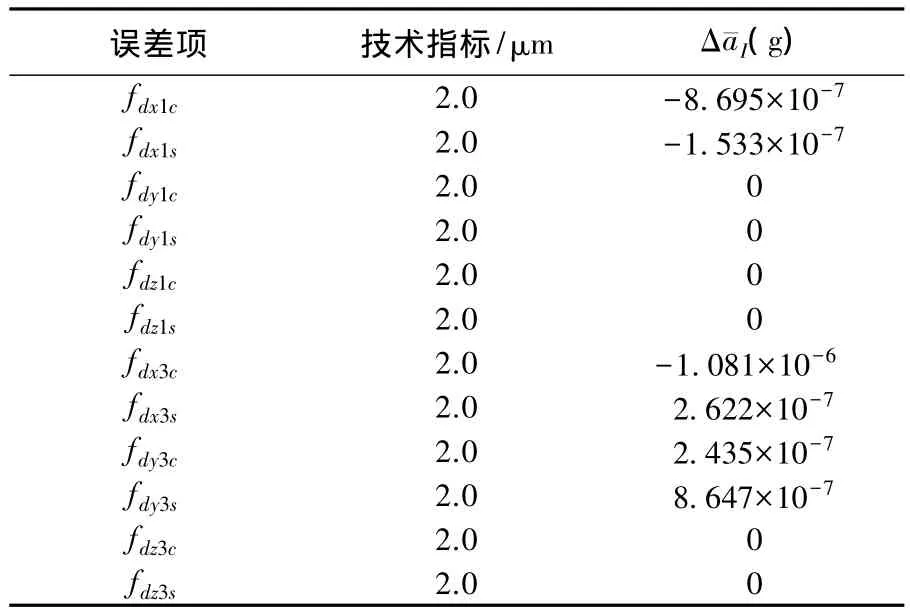
表4 反转平台反转时位移量误差对加速度计输入比力影响

图4给出了反转平台旋转时闭合误差与其通过离心机自身误差作用下产生的总输入比力误差之间的关系曲线.可以看出当闭合误差范围在0～2.5°时，其输入比力误差是随着闭合误差的增加而减小，误差绝对值增大;闭合误差范围2.5°～5°时，输入比力误差随着闭合误差的增加而增加，误差绝对值减小;闭合误差范围5°～15°时，输入比力误差随着闭合误差增加而增加，误差绝对值增加.当闭合误差不大于9.1°时，产生的总输入比力误差不大于1×10-6g.同样受测试设备及整周圈数选取的限制，通常将闭合误差放宽到10°，进而通过补偿掉该项误差以满足精度要求.

同时利用式(5)计算得到闭合误差作用离心机向心加速度所产生的加速度计输入比力误差，取闭合误差为4＇，则有

由此可见，向心加速度通过闭合误差作用产生的陀螺加速度计输入比力误差远远大于离心机自身误差所产生的误差，因此，该项误差实为反转平台同步反转测试时最为重要的误差.实际测试时，要将闭合误差精确地测出来，然后在陀螺加速度计的输出数据中补偿掉闭合误差引起的输入比力，从而满足标定精度要求.

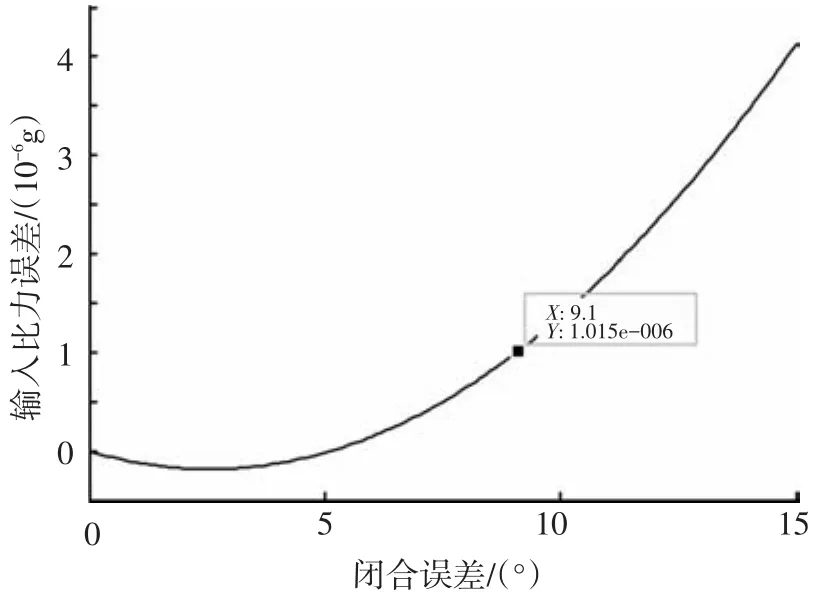
图4 反转平台旋转时闭合误差与总输入比力误差关系

综上可知在闭合误差为10°时，通过ω相关的离心机误差项作用产生的总输入比力误差项较大，需进行补偿.

需要说明的是表1和表2给出的数据都是以离心机旋转1周所产生的闭合误差为基础进行的输入比力影响计算，当离心机旋转周数增加时，相应的输入比力影响会随着时间的误差累计而增加，且与旋转周数成比例关系，因此要求若闭合误差较大时，离心机试验的主轴旋转周数尽量少，一般＜100周为宜.

上面对于离心机自身误差在闭合误差作用下对于其输入比力的影响给予分析，由此可知，只要保证闭合误差很小，则对于陀螺加速度计输入比力的影响很小，进而对于标定陀螺加速度计误差模型系数的影响也很小，满足10-6的精度要求.

2 主轴转速误差对输入比力的影响

下面分析主轴角速率误差对于离心机输入比力的影响，参考IEEE-836［4］标准关于角速度误差的分析，离心机主轴的角速率误差Δω影响离心机向心加速度的精度，即在离心机主轴角速率误差的影响下，输入比力为

在测试过程中，半径R0取标称值，则速率误差引起的平均输入比力可表示为

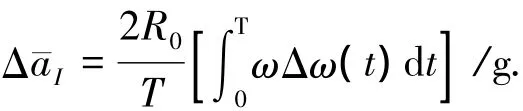
相应的Δω(t)包括速率漂移误差，速率误差以及速率平稳性．陀螺加速度计离心机试验过程中，平均主轴角速率ω的获取也是在主轴旋转整周的基础上完成的，因此离心机闭合误差所引起的测量时间误差会通过平均角速率影响陀螺加速度计输入轴的输入比力，进而影响陀螺加速度计误差模型系数的标定精度，则闭合误差引起的速率误差对于平均输入比力的影响为

其中n为离心机主轴旋转圈数．下面具体从角速率误差包含的3个方面进行分析．

2.1 速率漂移对于输入比力的影响

主轴的速率漂移是指离心机主轴速率随时间而变化，可以表示为Δω(t)=Ctω，其中C为速度漂移率系数．设试验时主轴速率漂移率为C=1×10-7/(2h)，主轴旋转一周误差40'，则10 g输入比力下(半径R0为2.5 m)离心机旋转100周时，速率漂移所产生的输入比力误差为

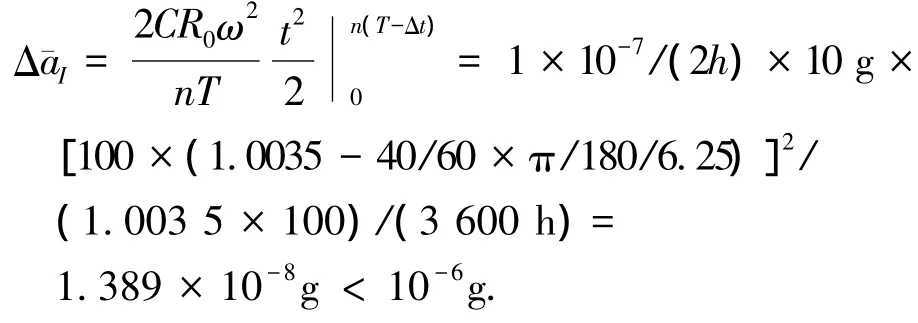
可见，角速率漂移误差与测试周数相关，当周数越大时，闭合误差部分贡献的输入比力误差越大;相反，短时间测试对于输入比力的影响较小，可以不做考虑.

2.2 速率精度对于输入比力的影响

速率精度相当于Δω(t)中的常值项Δω0，设试验用离心机主轴速率精度技术指标为0.5×10-6，其他参数选取与2.1节中一致，则10 g输入比力下旋转100周时，速率精度所产生的输入比力误差为

相对误差为9.98×10-7.

由此可见，速率精度对于陀螺加速度计输入比力的影响较大，且与闭合误差无关，实际标定误差模型系数时需要将该部分输入比力误差进行补偿.

2.3 速率平稳性对于输入比力的影响

速率平稳性是指主轴的速率随时间变化呈现周期性波动，可表示为Δω(t)=ωpsin(2πfwt+φ)．设试验时离心机的速率平稳性指标为5×10-7，则相当于幅值ωp为5×10-7，则离心机主轴旋转一周的平均输入比力误差为

若离心机旋转一周时间T-Δt恰为波动周期tw的整数倍，则可得该项积分为0;若为非整数倍关系，设(T-Δt)/tw的整数部分为10，|cos φcos(2π(T-Δt)/tw+φ)|可能取得最大值为2，则引起的输入加速度相对误差不超过3.3×10-8，若(T-Δt)/tw的整数部分为1，则不超过3.3×10-7．另外可知，速率平稳性对于陀螺加速度计输入比力的影响随着主轴旋转圈数的增加而减小.

综上，离心机存在闭合误差时，速率误差对陀螺加速度计的输入比力影响不大，但受测试时主轴旋转圈数的影响，当旋转圈数较多时，速率漂移对于输入比力误差的贡献较大，对速率平稳性的影响较小;反之当旋转圈数较少时，对速率平稳性的贡献较大，速率漂移的影响较小;对速率精度对输入比力的影响不依赖于测试圈数.由此可见，试验时需要折中选择合适的测试圈数来降低速率误差对于陀螺加速度计输入比力的影响，通常选择测试圈数为40～60圈.

3 地球自转角速度的影响

陀螺加速度计试验时，由于相对于惯性空间的角速度会影响加速度计的输出，因此考虑地球自转角速度ωe在非整周平均时对输入轴上的影响十分必要．下面从两种测试方法角度讨论闭合误差存在时地球自转角速度对加速度计输入角速度的影响．

3.1 反转平台不旋转

反转平台无旋转时相对于惯性空间的角速度在各坐标轴上的分量可表示为

对其进行积分可得

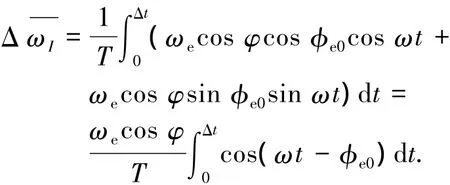
其中:ωe为地速，φ为当地纬度，φe0为初始数据采样时离心机大臂方向与地理北向的夹角．当闭合误差ωΔt≤10°=0.1745 rad，当地纬度φ=38.1°，可得

其中n为离心机主轴旋转周数，当n≥10时，

由此可知，反转平台不旋转，试验时离心机主轴旋转周数增加，即使存在闭合误差，也可削弱地球转速对陀螺加速度计输入角速度的影响.

3.2 反转平台同步反转

反转平台反转时相对于惯性空间的角速度在各坐标轴上的分量可表示为

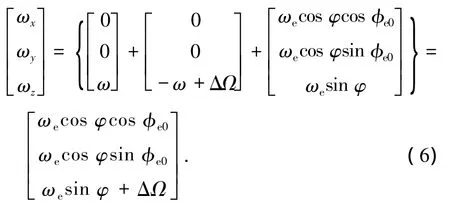
由式(6)可知，反转平台反转时各坐标轴角速率的分量不包含关于ωt的正余弦项，另外加速度计壳体相对于惯性空间的角速度在输入轴上的投影分量ωx=ωecos φcos φe0为常值，可根据φ与φe0的值进行补偿．由于离心机陀螺加速度计试验需要在多个不同主轴转速下进行时，才能对陀螺加速度计各误差模型系数进行辨识，在切换到不同转

速

时，φe0存在变化则由Δφie0引起的误差为

由上述分析可知，反转平台同步反转，当φe0确定时陀螺加速度计输入轴得到的角速度分量为一个常值．当主轴转速切换时，控制φe0的变化量可以满足10-6的精度要求．

综上，地球自转角速度对于陀螺加速度计输入角速度存在一定影响，实际标定过程中需要对该项误差进行补偿.

4 结论

1)在主轴旋转周数少，闭合误差角较小时，离心机自身姿态误差对于陀螺加速度计输入比力影响较小，若要满足10-6的精度，一般要求闭合误差≤10°.

2)角速率误差受闭合误差作用对于陀螺加速度计输入比力存在影响，其中速率精度对输入比力的影响最大，大于10-6g.同时该影响还受主轴旋转圈数的影响，因此测试时需选择合理的旋转圈数.

3)在闭合误差作用下，地球自转角速度对于陀螺加速度计输入角速度存在影响，反转平台无旋转时，试验过程中若满足主轴旋转圈数充足的条件，将削弱该影响;反转平台旋转时，控制φe0的变化量可以满足相应精度要求.

［1］王世明，任顺清.精密离心机误差对石英加速度计误差标定精度分析［J］.宇航学报，2012，33(4):520-526.

［2］王世明，任顺清.离心机误差对陀螺加速度计K2和K3项标定精度的影响［J］.纳米技术与精密工程，2013，11(2):140-145.

［3］王世明，任顺清，王常虹.在反转平台上标定陀螺仪的误差模型系数的方法［J］.中国惯性技术学报，2012，20(5):625-630.

［4］IEEE Aerospace and Electronics Systems Society.Std 836TM-2009，IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers［S］.New York:The Institute of Electrical and Electronics Engineers，Inc..1991.

［5］DEPUTATOVA E A，KALIKHMAN D M，POLUSHKIN A V，et al.Digital stabilization of motion of precision controlled base platforms with inertial sensitive elements.II.Application of float angular velocity sensor and pendulum accelerometers［J］.Journal of Computer and Systems Sciences International，2011，50(2):309-324.

［6］邢海峰.精密离心机误差对加速度计标定误差的影响研究［D］.哈尔滨:哈尔滨工业大学，2009.

［7］刘雨，郭刚，苏宝库.基于多加速度计组合的误差模型自标定方法［J］.航空精密制造技术，2011，47(6):9-12.

［8］李巍，任顺清，赵洪波.三轴转台误差对陀螺仪标定精确度的影响［J］.电机与控制学报，2011，15(10):101-106.

［9］SU Baoku，CHEN Cai，GUO Gang.Application of unscented Kalman filter in identification of INS error parameters based on centrifuge test［J］.Journal of Chinese Inertial Technology，2010，18(3):382-386.

［10］QIN Ran，GAO Yang，LI Mei，et al.Design of data acquisition system for dynamic simulation centrifuge test［C］//IEEE 2011 10th International Conference on Electronic Measurement and Instruments.Piscataway:IEEE，2011，2:147-150.