非对称环形桁架索网天线预张力设计解析算法
2015-09-21范叶森李团结马小飞李正军
范叶森,李团结,马小飞,李正军
(1.西安空间无线电技术研究所,710100西安;2.西安电子科技大学 机电工程学院,710071西安)
随着深空探测、远程通讯、地球观测等航天事业的发展,迫切需要发展大型空间可展开天线[1-4].在众多可展开天线的结构形式中,环形桁架索网天线因具有可折叠、质径比小、收缩比高、热稳定性优良等特点,成为国内外学者和工程技术人员研究的热点[5-9].
环形桁架空间索网天线结构设计的关键是合理配置索网中各段绳索的预张力,以使索网各节点稳定在理想的位置上,这是一个以“形”找“力”的过程[10-17].如果绳索中的张力分布不合理,实际节点位置和理想节点位置就会有偏差,从而产生设计误差[15-17].在索网天线中,绳索单元的数量通常大于自由节点数量的3倍,索网天线预张力求解是一个多解的问题,理论上满足索网结构平衡的预张力有无穷多组.为了保证索网结构的稳定性和抗干扰能力,人们提出了同一网面上的最大张力比(最大绳索张力与最小绳索张力之比)尽可能小的要求[9-17].根据国内外的研制经验[9-20],合理的一组绳索预张力必须满足使结构平衡和最大张力比尽可能小这项要求.
目前,常见的索网结构张力优化算法有以下几种:极小范数法[17]、平衡矩阵奇异值分解算法[14]以及把有限元法[11]、力密度法[12,20]和智能优化算法结合进行绳索预张力优化的综合算法[15]等.这些算法对推动空间索网结构设计技术的发展都起到了非常积极的作用,但这些算法必须通过大量的迭代运算才能得到最终的结果,并且用这些算法编写程序也较繁琐,应用存在一定难度.在工程上,为了减小收拢体积,副网的焦距通常大于主网的焦距,以缩小整个桁架的高度[16].目前,有关环形桁架索网天线张力优化算法的研究对象多为主副网对称的结构[16].事实上,对称结构是非对称结构的一种特殊形式,研究非对称结构能够得到更为一般的结论.
为提高运算效率,方便工程技术人员应用,本文发展了一种适用于非对称环形空间索网天线预张力设计的解析算法.只要给出主网绳索中的平均预张力,依次使用几个线性代数公式即可得到完全满足工程要求的绳索预张力.该算法不仅避免了迭代运算,而且在算法原理上不会产生设计误差,因而具有较高的计算效率和计算精度.
1 计算模型
图1所示为一个空间环形桁架索网天线计算模型[14,16],该型天线主要由主网、副网、张力阵和环形桁架4部分构成.主网、副网和张力阵均由芳纶纤维绳索制作,环形桁架为碳纤维管材.主网和副网为抛物面,在主网上铺设轻质金属网,用于反射电磁波.
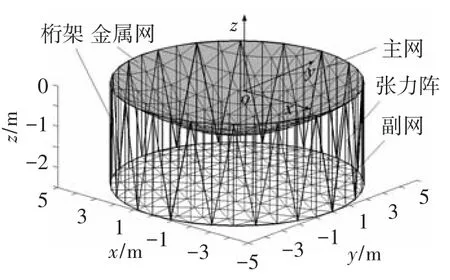
图1 环形桁架索网天线计算模型
为便于计算,以环形桁架上环面中心为坐标原点,建立整个计算模型的总体坐标系o-xyz,z轴与环形桁架中心线平行.张力阵中的绳索都与z轴平行,主网与副网在xoy平面内的投影重合.将与主网节点i相连(投影重合)的副网节点称为节点i的对应节点,并用表示该节点的编号;用绳索两端节点的编号共同表示绳索的编号,并将副网绳索称为主网绳索ij的对应绳索.如果分别用(xi,yi,zi)和(xi,yi,zi)表示主网节点i和副网节点的坐标,则xi=xi,yi=yi.为便于论述,将与桁架相连的索网节点作为固定节点处理,其他索网节点为自由节点.图2为索网结构中任一绳索所受张力的示意图.

图2 绳索张力示意图
图2中i、j为索网的任意两个节点,Tij、Eij、Aij、lij分别为连接i、j两个节点绳索ij的张力、弹性模量、截面积和两节点之间张紧状态的绳索长度,且lij满足:

2 理论推导
2.1 索网预张力设计方法
2.1.1 主网预张力计算
为保持平衡,主网各自由节点在3个方向所受的合力都必须为零.太空环境是一个无重力环境,因此在空间索网结构预张力优化的过程中,无需考虑重力作用,作用在自由节点上的力只有绳索张力.因为主网绳索作用在各自由节点z向合力可由与该节点相连的张力阵绳索中的张力去平衡,主网绳索的预张力只要能够使各节点在x向和y向平衡,主网中所有自由节点就都是稳定的.即只需要研究主网在xoy平面内投影的平衡问题,就能找到使主网平衡的绳索预张力.自由节点i在x向和y向的平衡方程为

式中:j为与节点i相连的第j个节点编号,e为与节点i相连的主网绳索总数.则主网所有自由节点在x向和y向的平衡方程为

式中:U为力平衡方程的系数矩阵,T为主网绳索预张力组成的向量,ns为主网中自由节点,r为主网中绳索单元数.
基于平面索网结构预张力优化极小范数法[17]的基本原理,结合以上分析,可以得到一组主网预张力的优化解为
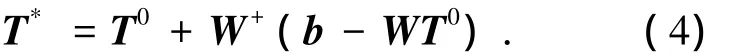
在用式(4)进行计算时,只要根据工程要求给定主网的平均预张力,就可以求出一组使主网在x向和y向平衡的预张力,而z向的平衡通过合理配置张力阵绳索预张力实现.
2.1.2 张力阵预张力计算
式(4)是式(3)的一组解,利用式(4)求出的绳索预张力必然可以使主网中的自由节点i在x向和y向平衡.为了使主网节点i处于平衡状态,还必须合理配置与节点i相连的张力阵绳索预张力 Tii.为了让节点 i在z向平衡,Tii必须与主网绳索作用在节点i上的z向合力相等,即
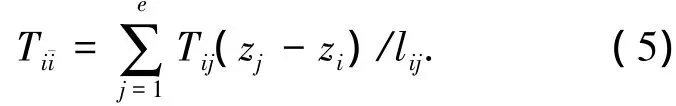
2.1.3 副网预张力计算
如果主网与副网是前后对称的结构,即主网焦距f1与副网焦距f2相等,则副网绳索预张力与对应位置主网绳索预张力取相同值就能使副网处于稳定状态.
如果主网与副网不是前后对称的结构,即f1≠f2,则副网与主网绳索ij对应位置绳索ij中的预张力 Tij可取为

式中 lij为主网绳索 ij在副网对应绳索 ij的长度.
2.2 索网结构平衡论证
由以上论述可知,绳索预张力必须使索网各节点都稳定在理想位置.式(4)和式(5)求出的绳索预张力都是根据主网的静力平衡方程得到的一组解,由式(4)和式(5)求出的绳索预张力一定能使主网各节点稳定在理想位置.如果根据式(6)求出的副网绳索预张力能使副网稳定在理想位置则整个索网系统就处于平衡状态.
不失一般性,取与主网任一自由节点i对应的副网节点i进行分析.副网中节点i在x和y向合力为

把 xi=xi,yi=yi和式(6)代入式(7)可得

把式(2)带入式(8),可得

由式(9)可知,副网在x和y向是平衡的.
因为主网和副网都为抛物面,可设主网的抛物面方程为

副网的抛物面方程为

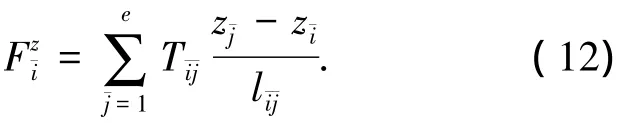
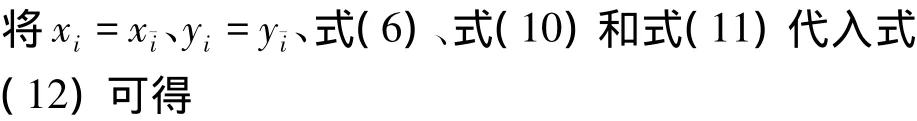

将式(5)带入式(13)可得

由式(14)可知,副网作用在节点i上的z向合力与张力阵绳索作用在该节点上的力大小相等方向相反,是一对平衡力,因此该节点在z向也是平衡的.
综上可知,使用式(4)~(6)计算得到的绳索预张力可使整个索网系统都处于平衡状态,各节点都稳定在理想位置.即只需要根据设计要求,给出一个主网绳索预张力的平均值,就可以求出一组使主网平衡的绳索预张力,然后根据主网的纵向平衡方程,就可求出张力阵绳索张力;当求出一组主网的平衡预张力后,让主网绳索中的预张力分别与特定的系数相乘,就可以得到一组使副网平衡的预张力.
2.3 绳索初始长度计算
绳索的初始长度是绳索裁剪的依据,为绳索在无应力状态下的长度.在求出每段绳索ij的预张力Tij后,可求出绳索ij的初始长度为
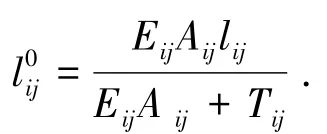
3 算例分析
为进一步验证本文算法的正确性、可行性和有效性,便于将计算结果进行对比,下面对一个具体算例进行分析.
根据文献[16-17],选取图1所示计算模型的结构参数,天线口径10 m,前索网抛物面焦距f1=6 m,后索网抛物面焦距f2=40 m.为了用非线性有限元法对计算结果进行验证,还需要补充一些结构参数.选取主网绳索预张力的平均值为20 N,直径为1 mm,绳索的弹性模量为20 GPa,环形桁架高度为2.5 m.把采用本文所提算法计算得到的绳索预张力转化为绳索初始应变后,将预张力优化结果导入ANSYS软件进行非线性有限元分析,绳索单元为Link10,把各节点的理想位置作为各节点的初始位置,索网结构有限元模型如图3所示.
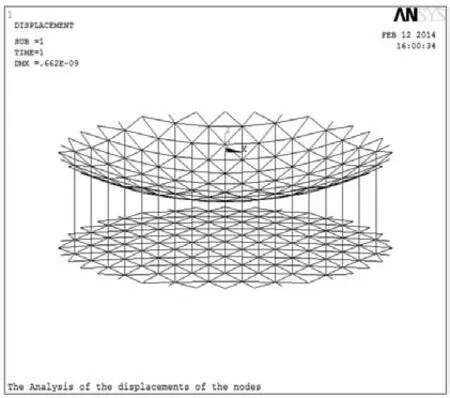
图3 索网结构有限元模型
对于具体的工程来说,如果各节点位移都处在一个较小的范围(1×10-6mm)内,就可以认为整个索网结构处于稳定状态.经过ANSYS计算,整个索网结构各节点的最大位移为0.662×10-9mm,因此整个索网系统处于稳定状态,采用本文所提算法得到的绳索预张力可以使索网各节点稳定在理想位置.
为进一步论述本文所提算法的可行性,把本文算法计算结果与其他算法的计算结果做一比较.当取主网的平均预张力为20 N时,采用本文算法计算得到的主网张力阵和副网的预张力最大和最小值如表1所示.

表1 预张力优化结果 N
计算出全部绳索的预张力后,即可以计算不同部位绳索预张力的最大张力比.文献[16-17]都对图1所示计算模型的预张力优化问题进行了研究,并且主网和副网的结构尺寸与本文所选取结构尺寸相同.文献[16-17]及本文算法得到的绳索预张力的最大张力比如表2所示.

表2 不同算法得到的预张力的最大张力比
由表2可知,本文算法得到的计算结果全面优于文献[17]的计算结果;副网预张力优化结果优于文献[16]方法的计算结果,主网预张力的最大张力比略大于文献[16]方法的计算结果,差值为3.95%.
文献[14]采用平衡矩阵奇异值分解算法对一个前后对称的索网天线预张力进行了优化计算,主、副网结构尺寸与本文所用计算模型主网尺寸相同,文献[14]得到的主网预张力的最大张力比为1.38;对于这一模型,用本文算法得到主网预张力的最大张力比为1.29.本文所提算法得到的计算结果优于文献[14]所提算法的计算结果.考虑到把力密度法、有限元法和智能优化算法(如遗传算法)结合进行预张力优化的综合算法会产生一定的设计误差[10],本文不再与这些综合算法的计算结果进行对比.
综上,本文的解析算法所得计算结果总体上优于或接近目前常见的几种高精度空间索网结构预张力优化算法;同时,相对于其他算法,本文提出的解析算法避免了迭代,减小了编程工作量,提高了计算效率,更便于工程应用.采用matlab内部计时器进行计时,对图1所示的计算模型进行一次预张力优化计算的时间为0.0491 s.
4 结 论
1)提出一种适用于非对称环形桁架索网天线预张力设计的解析算法,并给出该算法的计算步骤,对于结构确定的环形桁架索网天线,只需给出主网的平均张力,就可以根据式(4)~(6)求出一组满足设计要求的绳索预张力.
2)理论推导、数值仿真以及与其他算法的比较表明,本文所提算法正确、可行和有效,可用于对称或非对称环形索网天线绳索的预张力优化计算.
3)算法避免了常规算法中普遍存在的反复迭代求解的步骤,理论简洁,具有较高的计算效率,便于工程应用.
[1]HIGUCHI K,KISHIMOTO N,MEGURO A,et al.Structure of high precision large deployable reflector for space VLBI[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference.Palm Springs:AIAA Press,2009:AIAA 2009-2609.
[2]ORIKASA T,MIURA A,HIROYUKI T,et al.A Study of large reflector antenna mounted on communication satellite for satellite terrestrial mobile communication system[C]//31st AIAA International Communications Satellite Systems Conference.Florence:AIAA Press,2013:AIAA 2013-5649.
[3]TANAKA H.Surface error estimation and correction of a space antenna based on antenna gain analyses[J].Acta Astronautica,2011,68:1062-1069.
[4]THOMAS W M.Historical perspectives on the development of deployable reflectors[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Palm Springs:AIAA Press,2009:AIAA 2009-2605.
[5]SHI H,YANG B,THOMSON M,et al.A nonlinear dynamic model and free vibration analysis deployable mesh reflectors[C]//52nd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference.Denver:AIAA Press,2011:AIAA 2011-1999.
[6]SHI H,YANG B,THOMSON M,et al.Automatic surface mesh generation for design of space deployable mesh reflectors[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference.Honolulu:AIAA Press,2012:AIAA 2012-1840.
[7]杨东武,尤国强,保宏.抛物面索网天线的最佳型面设计方法[J].机械工程学报,2011,47(19):123-128.
[8]SHI H,YANG B,FANG H.Offset-feed surface mesh generation for design of space deployable mesh reflectors[C]//14th AIAA Gossamer Spacecraft Forum.Boston:AIAA Press,2013:AIAA 2013-1526.
[9]YANG B,SHI H,THOMSON M,et al.Optimal design of initial surface profile of deployable mesh reflectors via static modeling and quadratic programming[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference.palm springs:AIAA Press,2009:AIAA 2009-2173.
[10]MA X,SONG Y,LI Z.Mesh reflector antennas:form finding analysis review [C]//54th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Boston:AIAA Press,2013:AIAA 2013-1576.
[11]李团结,周懋花,段宝岩.可展天线的柔性索网结构找形分析方法[J].宇航学报,2008,29(3):794-798.
[12]边鹏飞.环形桁架可展开天线的找形与动力学分析[D].西安,西安交通大学,2012:1-34.
[13]LI Tuanjie,JIANG Jie,DENG Hanqing,et al.Formfinding methods for deployable mesh reflector antennas[J].Chinese Journal of Aeronautics,2013,26(5):1276-1282.
[14]李刚,关福玲.环形桁架展开天线索网的预拉力优化技术及工程应用[J].固体力学学报,2006,27(专辑):174-179.
[15]GUAN Fuling,DAI Lu,XIA Meimeng.Pretension optimization and verification test of double-ring deployable cable net antenna based on improved PSO[J].Aerospace Science and Technology,2014,32(1):19-25.
[16]杨东武,保宏.非对称索网抛物面天线力平衡特性及预拉力设计[J].机械工程学报,2009,45(8):308-312.
[17]杨东武.星载大型可展开索网天线结构设计与型面调整[D].西安,西安电子科技大学,2010:55-80.
[18]MORTEROLLE S,MAURIN B,QUIRANT J,et al.Numerical form-finding of geotensoid tension truss for mesh reflector[J].Acta Astronautica,2012,76:154-163.
[19]LIU W,LI D.Simple technique for form-finding and tension determining of cable-network antenna reflectors[J].Journal of Spacecraft and Rockets,2013,50(2):479-481.
[20]CHU Zhengrong,DENG Zongquan,QI Xiaozhi,et al.Modeling and analysis of a large deployable antenna structure[J].Acta Astronautica,2014,95:51-60.
