基于电网中枢点识别的无功电压控制分区方法

成 煜，杭乃善

（广西大学 电气工程学院，广西 南宁 530004）

0 引言

二级电压控制分区是电网电压自动控制（AVC）的关键环节，合理的无功电压分区与中枢点的选择对提高电压控制的质量、为上级优化进一步提高经济性起重要作用。对于无功电压控制分区，已经有了较为成熟的研究成果[1-4]。主要以潮流方程雅可比矩阵无功电压线性化灵敏度关系为标度表征电网各节点之间的无功电压耦合性，各种聚类算法已广泛应用于分区之中[2-9]。

中枢节点是某些能反映全网的电压水平的节点，尤其是电网中少数拥有较高输电电压等级的大容量枢纽变电站，一般具有调压能力、联接的负荷支路较多、有较大无功调节量的发电厂等特点。实际上，对一定层级电网，自动电压闭环控制监控的中枢母线并不唯一，这在省调、地调AVC系统中较明显，本文主要从网调层面，从对全网优化起关键约束的中枢节点的角度分析确定电网中枢母线。在二级电压控制中中枢点电压执行上级优化电压指标，将电压控制在设定值范围内。可调节无功发电厂作为系统的最主要无功源，也是最直接、最经济的调压手段，对系统电压运行水平有重要影响。电气距离的变化、网架结构的复杂、发电机调节本身的局限性，使得串并联电容、同步调相机、有载调压变压器分接头调节作为重要的辅助调压方式，实现各节点无功电压就地平衡，这也是三级电压控制中执行环节的主要内容。

对于无功电压分区，传统方法是先由各聚类算法实现二级电压控制分区的划分，再在各分区主要应用优化算法确定中枢节点。文献[2]针对每个PV节点，每次松弛为PQ节点，设置新的平衡节点，经多次形成考虑准稳态调节过程的无功电压全维度灵敏度矩阵，将机组与负荷节点同时进行聚类分区。文献[4-5]用模糊聚类算法对IEEE 39节点网络进行电压分区，对分区可能存在的孤立节点、PV节点，按电网物理连接距离进一步归并。文献[5]分别将谱系数平均距离法和模糊C均值聚类算法应用于河南电网进行电压分区，依据负荷节点可控性与可观性灵敏度并由贪婪算法实现分区中枢节点选择。文献[7]针对分区中枢节点数量难以确定的问题，通过引入多元统计分析理论中的主成分分析与因子分析方法确定中枢节点。文献[9]在能量函数数学模型的基础上构建能量/电压灵敏度矩阵，并由模糊聚类算法实现电压分区。文献[10]用粒子群优化算法设计目标函数，将二级电压分区与各区中枢点选择同时进行。文献[11-13]计及各无功电压控制分区间的相互影响，对紧急工况下协调区域间无功支援进行建模仿真。

本文优先考虑最高级即三级电压所需优化控制的全网中枢点，先将所有PV节点的机端电压放开不设限制，松弛为PQ节点，利用注入电流形式的潮流方程，通过潮流计算不断识别电压越限点并由电压相关性灵敏度进行校正直到无电压越限点。控制中枢节点电压并代入潮流方程校验，确定全网中枢节点。将各中枢点确定为全网无功电压所需分区数目，建立无功源控制空间，引入云聚类算法[14]，将和中枢节点母线电气相关性大的厂站母线组成一个控制分区，进一步调整，完成电网所有节点的无功电压分区。对IEEE 14、IEEE 30节点输电网络进行了仿真验证。

1 灵敏度分析

1.1 注入电流形式的潮流方程

注入电流形式潮流计算节点功率方程推导如下，n节点交流系统的节点电压方程为[15]：

式（1）中，对系统任意一个节点i，其注入电流Ii为：

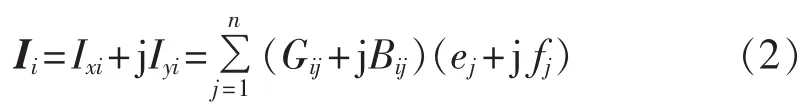
将式（2）左边注入电流的实部、虚部分开表示：

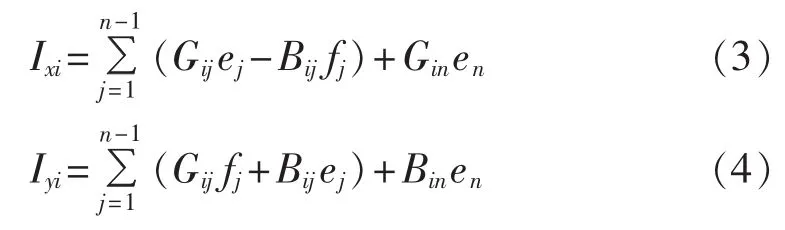
其中，i=1，2，…，n-1。

将式（3）、（4）表示成如下矩阵形式：

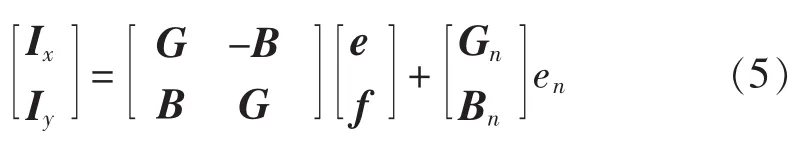
节点注入功率可表示为电压与节点电流乘积的非线性形式，如式（6）所示：

其中，第n个节点为平衡节点；G、B分别为n-1阶节点导纳矩阵的实部和虚部；Gn、Bn分别为节点导纳矩阵与平衡节点所在列相关的实部与虚部；en为平衡节点电压的实部。对于常规PV节点，可在式（6）迭代求解过程中对ei、fi依然取节点电压幅值Ui恒定作为迭代限制条件。在潮流计算中给定电压平启动初值，逐次迭代逼近直到满足收敛性要求。经换算和矩阵求逆得直角坐标下电压实部、虚部与节点注入电流实部、虚部间迭代方程的线性化矩阵形式，即：

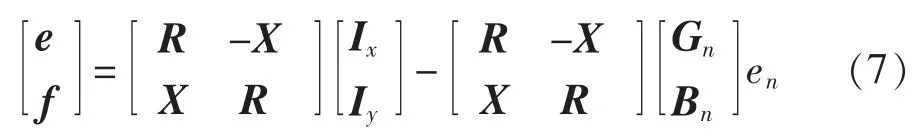
其中，X=-（B+GB-1G）-1；R=-B-1GX。 这样，由式（5）或式（7）与式（6）联立，交替迭代求解直到节点电压实部、虚部达到收敛要求。

1.2 无功电压灵敏度推导

无功电压控制灵敏度多由牛顿拉夫逊法潮流计算雅可比矩阵中令ΔP=0，推导出ΔU/ΔQ的灵敏度关系，也有直接用有功无功解耦的快速算法中取无功电压迭代矩阵。对于注入电流形式的潮流方程，则将式（7）两边微分线性化有：

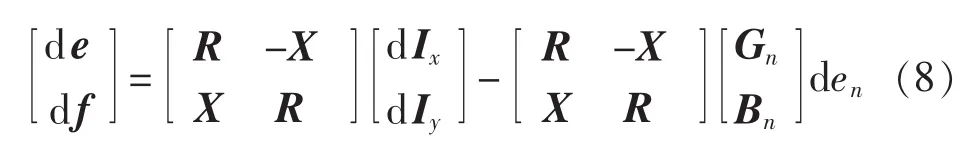
而对于高压输电网络，因Rij≪Xij，即线路电阻远小于电抗，故可近似取Rij=0，则有：

同理对节点j有：

由式（11）、（12）对同一注入无功电流 Iyk的灵敏度，可将节点电压Ui与Uj相关联。即可得系统节点电压间的相关性灵敏度为：

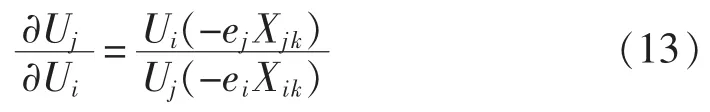
节点电压幅值主要决定于节点电压实部，当近似取 Ui≈Uj、ei≈ej作估算，则：

由式（9），节点电压实部主要与节点注入无功电流相关，其相关性灵敏度为-X。它将节点无功调整与电压幅值的相关性用注入电流与电压实部的线性网络关系表示出来。式（14）是节点电压幅值之间的相关性灵敏度。

1.3 系统网损对电压灵敏度

对中枢点电压进行调节控制，在三级电压控制中确定中枢点电压约束范围，无功电压调节的网损经济性是重要指标。

有功网损为：

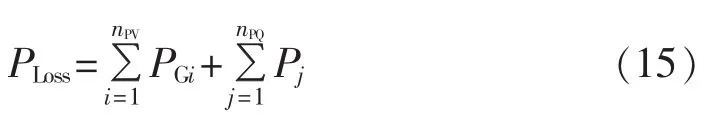
代入式（6）可得：

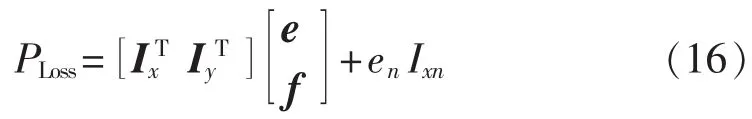
代入式（5）可得：

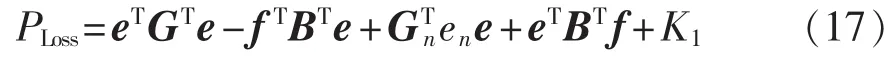
其中，K1为与节点电压实部无关的常量；对高压输电网，nPV、nPQ分别为全网PV、PQ节点的数目。取Gij≫Bij，考虑节点电压幅值主要由电压实部影响，则有系统有功网损对电压实部的灵敏度：

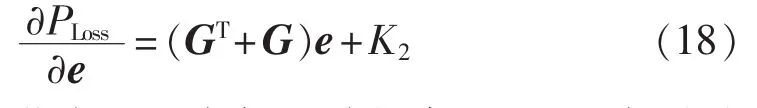
其中，K2为与节点电压实部无关的常量，这也表明对于系统中枢点，其电压约束范围或上限值越高，其对有功网损的灵敏度越大，合理调控该节点电压就能提高系统运行的经济性。

2 中枢节点的确定与校验

2.1 电压中枢点及其识别步骤

电力系统电压由无功电源调节，因电源、无功设备的配置及其调控能力的局限性，要满足全网的电压水平，可利用有无功调节容量的发电机来侧重控制少数中枢节点的电压在一定范围内，进而使全网电压满足要求且能减轻分散调压的负担。本文中枢点考虑主要从能为全网优化经济运行提供有效节点电压约束条件，从网调AVC角度出发分析确定。电网电压是电能质量、系统安全性和经济性等运行水平的反映，故各点电压均须在所希望的电压偏移内，如输电网络中的UN～1.05UN（UN为该电压等级输电网的额定电压）。当中枢点电压达到其上限值，有助于减少系统网损和提高系统的电压稳定性。在具体计算中，将发电机节点松弛为PQ节点，即测试在全网机组无功功率全部额定发出时，在相对正常运行条件下无功功率极大充裕时，系统中出现的电压幅值越限的发电厂母线或变电站节点，形成该条件下的越限点集，那么中枢点就在这集合当中。中枢点电压应能影响尽量大的区域，使该区域各点电压值也符合运行的电压质量要求，以该中枢点为中心，根据无功电压相关性可确定有效电压分区。

因此，本文通过先将除平衡节点以外的发电机节点松弛为PQ节点，使机组无功功率输出达到上限值，设置电压越上限值，再由式（5）经潮流计算，可识别出发电机无功满发条件下节点电压幅值越限点，即若令中枢点电压幅值范围为[Umin，Umax]，当 Ui＞Uimax或者Ui＜Uimin，则将出现电压不等式越限。令SU=为电压无限制条件下的越上限电压节点的集合。

取k为SU中一电压越限集中电压最高节点，则令其取电压上限值，根据与越限值的电压幅值差，由与其余节点电压的相关性灵敏度，对除平衡节点及该越限节点外的节点（j=1，2，…，k-1，k+1，…，n-1）电压收敛值进行校正，即：

则相应对其他节点j的电压变化量为：

经校正，新的越限电压的集合为：

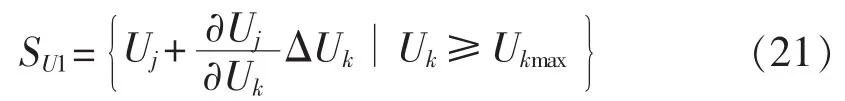
式（19）—（21）从最初的越限电压集开始不断进行电压校正，直到把所有越限点电压幅值取上限后，系统所有电压都不越限为止，则这些取其电压上限后使全网节点电压稳定在约束范围内的越限点就是电网中枢节点。

因此，本文所提出的电压中枢点的识别步骤如下。

a.先设定节点电压上、下限，即[Umin，Umax]，将除平衡节点外所有PV节点松弛为PQ节点进行注入电流潮流计算，估算电网电压。由式（5）形成越限电压集合SU并将越限电压降序排列。

b.对越限电压集合中的最高电压点，按式（19）得其须降低的电压ΔUk且修正当Uk不越限后各点的电压，形成新的越限电压集合SU1。不断校正并形成新的越限电压集直到无越限电压。

2.2 中枢节点的校验

对于识别出的全网中枢节点集，令每个中枢节点电压取其电压上限值即为确定量，即：

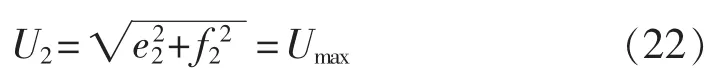
而其余节点电压为待求量：

则式（7）可进一步分块调整表示为：

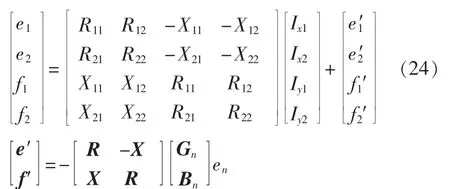
将电压方程拆分为：

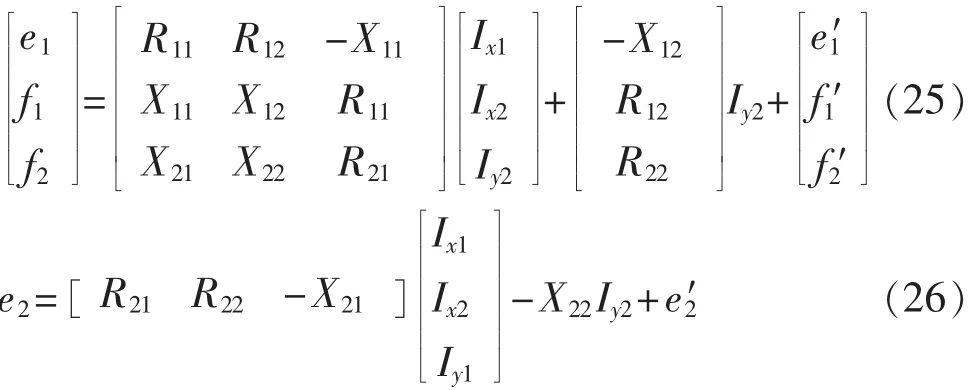
设f2≪e2，近似将中枢点电压实部取成电压上限幅值，即令e2≈Umax为边界值，则中枢节点注入无功电流为：

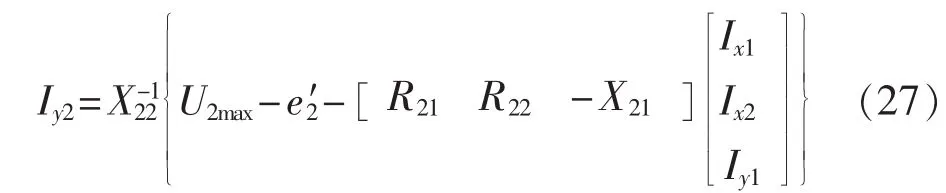
其中，Ix1、Iy1、Ix2为由 2.1节步骤 a计算所得的未设定中枢节点且系统全PQ节点时的相应节点注入电流收敛值。

进一步将式（27）得出的 Iy2回代入式（25），可得相应的各节点电压实部、虚部，即 e1、f1、f2，如果校验后U1、U2均无越限且中枢点电压在上限值，说明该中枢点集的确定是合理的。

3 云聚类算法完成无功电压分区

3.1 云聚类算法

云模型是用自然语言同时考虑分类边界的模糊性及事件发生的随机性，将定性描述转换成定量表示的数学模型[16-18]，能较好地反映自然概念的不确定性，反映随机性和模糊性之间的关联。

设U是一个用精确数值表示的定量论域，C是U上的定性概念，若定量值T是定性概念C的一次随机实现，则 T 对 C 描述的准确度 μ（T）∈[0，1]是有稳定倾向的随机数。T在论域上的分布称为云分布，每个T称为一个云滴[15-17]。正态云所处的概念特征可表示为（Ex，En，He）。 Ex为 T 的期望；En为 T 的标准差；He为T的方差，表示离散程度。云滴可由云发生器产生，本文用到逆向正态云发生器及T云发生器2种云发生器[17]。

（1）逆向正态云发生器。 输入为（T1，μ1）、（T2，μ2）、…、（Tm，μm），输出为（Exi，Eni，Hei）（i=1，2，…，m）。

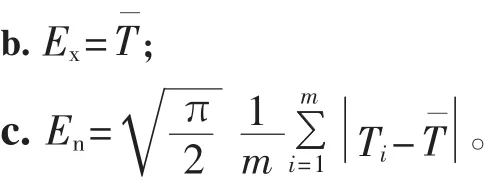
（2）T 云发生器。 输入为（Exi， Eni， Hei）（i=1，2，…，m），输出为（T1，μ1）、（T2，μ2）、…、（Tm，μm）。

a.En′=rand（En，He），即取 En和 He之间的随机数；

正态云滴生成后经云运算逐步进行概念水平提升形成高层次概念的正态云滴[17]。而电压分区数或第2节所定中枢点数决定了最终生成的高层次概念正态云滴的个数。每个高层次正态云滴代表一个强概念云团，可视作强耦合或相关性高的节点集，中枢节点是其耦合中心。依据最初各正态云滴具体特征参数，通过云发生器计算对最终生成的高层次概念云团的隶属度，实现对云滴的聚类软划分。由于建立无功源控制空间[2]并实现向云模型的转换，相应地也就实现了对全网节点向相关度高的中枢节点的聚类软化分。

通过建立无功源控制空间，进一步确定各节点间的电气距离，通过计算负荷节点每次合并过程中的相对距离（即每次合并的最小距离与最大距离比）分析比较聚类算法的优劣，每次聚类中相对距离越小表示对节点的聚类划分越彻底，相应地，该算法对节点间无功电压耦合关系解耦得越彻底。

应用文献[2]中方法对云聚类算法与改进Ward聚类算法应用于IEEE30节点系统的24个负荷节点聚类过程比较结果如图1所示，图中相对合并距离为标幺值。

由图1可见，对于纵轴任一聚类过程而言，应用云聚类算法的相对距离要远小于改进Ward算法，从而对系统无功电压解耦的效果更好。

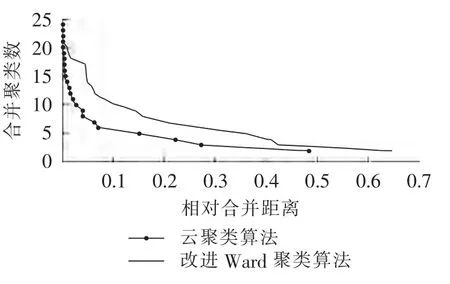
图1 相对合并距离Fig.1 Relative merging distance

3.2 无功电压分区步骤

a.建立无功源控制空间。对n-1阶线性网络灵敏度（不包含平衡机组）取其绝对值，取所有节点与系统所有无功功率可调发电机组之间的灵敏度矩阵，进一步形成（n-1）×nPV维的负荷节点空间灵敏度矩阵，n-1是除平衡节点外的节点数，nPV是全网所有的发电机节点数。将节点映射到由各控制机组组成的无功源控制空间[2]，每个负荷点的nPV维参数即具体灵敏度值是对其在无功源控制空间[1]无功电压特性的定量描述。

b.形成正态云滴。将n-1个节点在无功源控制空间的定量值经逆向云发生器处理，形成与该节点相对应的正态云滴的具体属性表示，即（Exi，Eni，Hei），从而完成向云模型的转换。在云模型中，Ex表征节点对应云滴归并到相应电压分区的期望度量值；En表征节点对各个电压分区都存在无功耦合，即模糊性度量值；He表征节点对各电压分区隶属的随机性度量值。

c.以确定的若干中枢节点（由步骤b也形成相应正态云参数）为聚类中心或高层次概念的云团，将由逆向云发生器形成的各正态云滴具体参数输入到T云发生器，生成各节点的相应云滴对于各云团的隶属度μi。每个正态云滴根据其隶属度大小聚合到对其隶属度最大的高层次概念云团，从而完成各节点向各中枢节点正态云滴的聚合。

d.完成对各个分区的进一步调整，确定最终分区。按照平衡机组的实际并网位置归并其分区[19-21]。对于初步分区所得可能的孤立节点或者分区中只含负荷节点而没有无功控制机组的情形，将根据该节点在无功源控制空间与各台机组的相关性灵敏度进行归并。

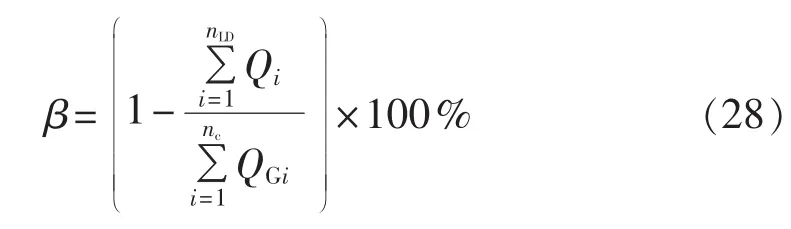
e.对完成的分区进行无功储备校验。定义无功储备裕度为：其中，nLD、nc分别为分区中负荷节点数与无功控制机组数；Qi为分区任一负荷节点的注入无功功率；QGi为分区中发电机节点的无功裕量。取无功功率裕度最少为15%，若分区无功裕度未达到标准，则综合相邻分区无功裕度，重新调整无功负荷较大节点的分区归属。

4 算例验证

本文选取IEEE 14、IEEE 30节点输电网络进行仿真测试，IEEE 14节点网络有5台发电机、14个节点。IEEE 30节点网络有6台发电机、30个节点。用MATLAB2009软件编写程序。

4.1 对IEEE 14节点系统仿真测试

由前述方法，根据式（5）或者式（7）对全PQ节点（除平衡节点外）系统进行注入电流形式潮流计算，初始的收敛电压值如表1所示（表中电压均为标幺值，后同），根据该系统电压运行水平较高，设置中枢点电压约束范围为[0.9，1.05]p.u.，则根据其上限1.05 p.u.，代入式（19）—（27）进行中枢点识别与校验，表1中校验后节点电压为将中枢点电压取上限后的系统电压，可以看出没有节点越下限0.9 p.u.，因此该中枢点的确定是合理的。该网络中枢节点为节点 6、7、8。

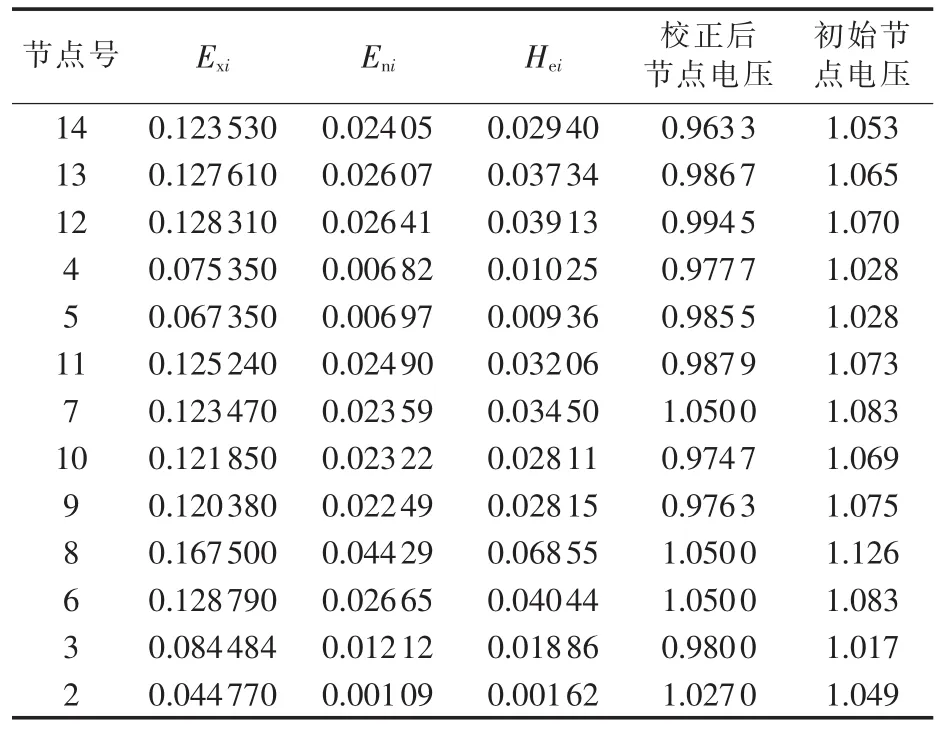
表1 IEEE 14节点系统潮流校验结果及节点云模型生成Table 1 Power flow verification results and cloud model generation of IEEE 14-bus system

建立无功源控制空间[2]后，由逆向云发生器生成的各个节点对应云模型中的正态云滴具体参数（Exi，Eni，Hei）如表1中所示。 确定出系统中枢点，由云聚类算法完成以各中枢点为云团或中心的聚类软划分，电压分区结果如表2所示。实际分区并不能将PV节点完全等同于正的负荷节点形式PQ节点，进一步分析各机组实际并网情况，将节点8并入分区3，完成IEEE 14节点系统的聚类划分。由于IEEE 14节点系统机组无功总量为95.39 Mvar，恒定功率无功负荷为73.5 Mvar，系统无功较为充裕，根据校正后潮流收敛结果及式（28）计算结果综合考虑，各分区无功储备裕量取100%。

表2 IEEE 14节点系统中枢点识别及云聚类分区结果Table 2 Results of pilot node identification and cloud clustering partitioning of IEEE 14-bus system

表3将本文方法与文献[20]方法对IEEE 14节点网络分区结果进行比较，只有节点11的分区归属不同，且本文先通过中枢节点识别已确定分区数，并通过分区无功校验该分区的合理性。图2为IEEE 14节点网络最终分区效果图。

表3 本文方法与文献[20]分区结果比较Table 3 Comparison of partitioning results between proposed method and method in literature[20]

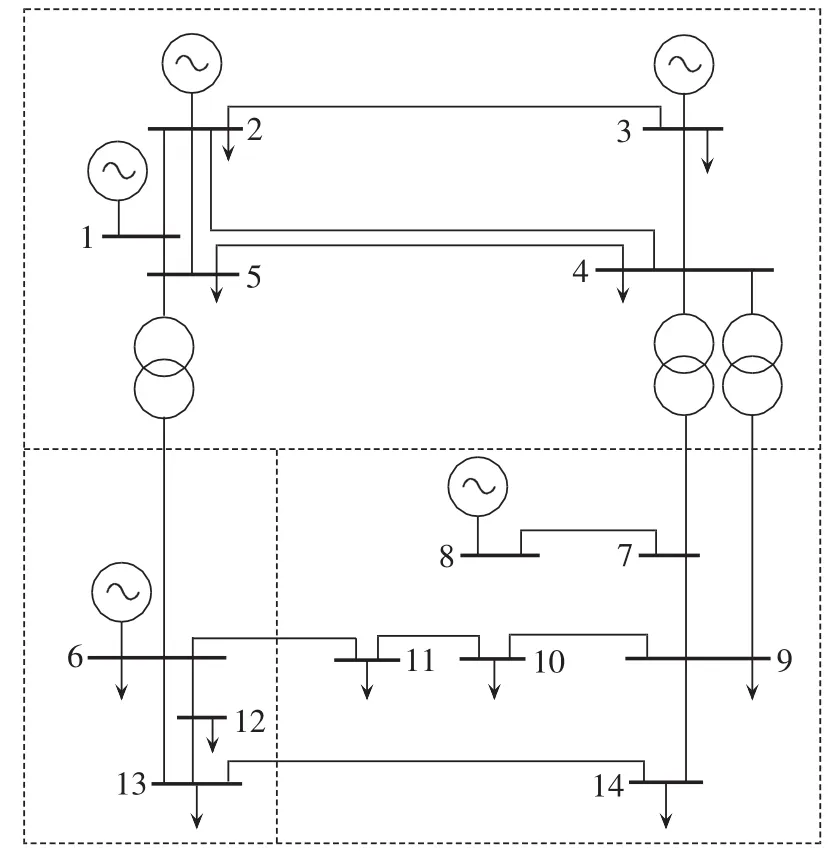
图2 IEEE 14节点输电网络最终分区示意图Fig.2 Schematic diagram of final partitioning results of IEEE 14-bus system

4.2 对IEEE 30节点系统仿真测试

对IEEE 30节点网络，根据表4初始潮流计算节点电压水平，设定约束范围取[0.9，1.02]p.u.，则经校验，判别出的越限节点 2、3、11、13电压取上限值1.02 p.u.后，所有节点电压均不越下限，在约束范围内，从而确定其为中枢节点。在此基础上根据云聚类算法步骤，完成以节点2、3、11、13为中心的分区4无功电压划分，初次划分结果如表5所示。值得关注的是，4个中枢点中有3个是发电厂高压母线，并且出现中枢节点2、3孤立的情况，由于节点2是发电机节点，可根据其实际并网位置进一步调整分区，中枢节点3是枢纽变电站节点，根据其在无功源控制空间[2]中对各发电机组无功电压灵敏度最大原则，进一步归并到对其无功电压控制最灵敏的发电机组所在分区中。

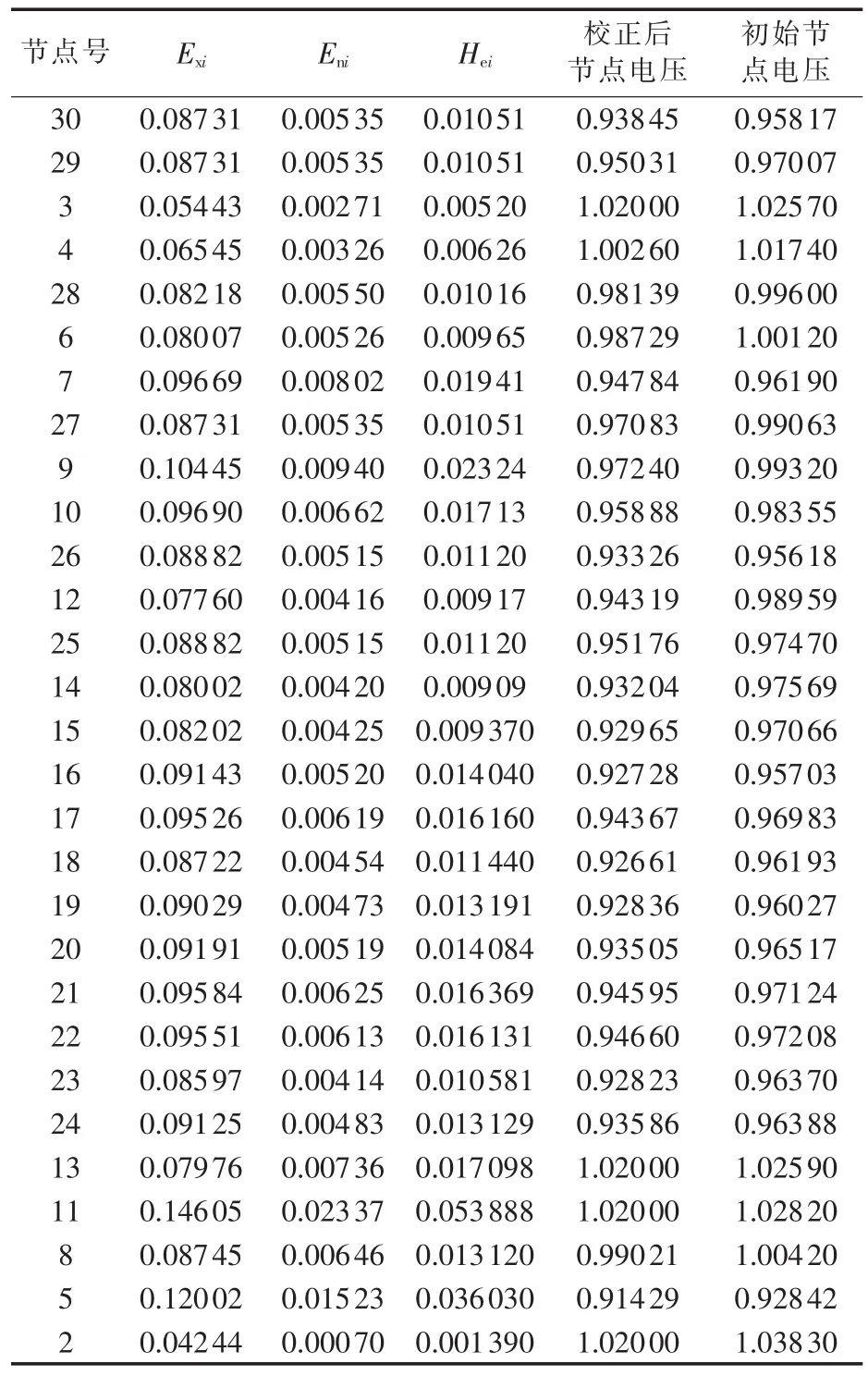
表4 IEEE 30节点系统潮流校验结果及节点云模型生成Table 4 Power flow verification results and cloud model generation of IEEE 30-bus system

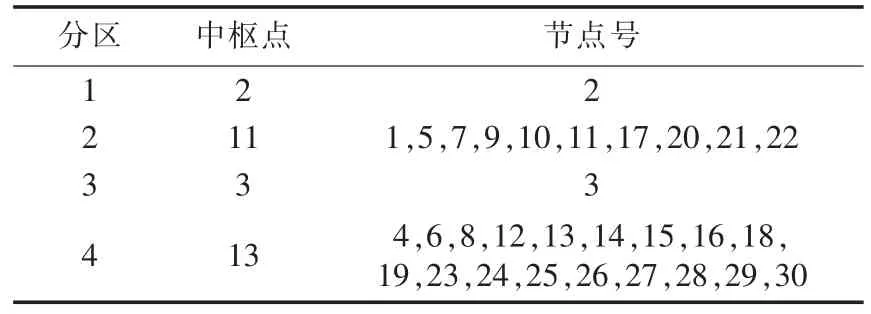
表5 IEEE 30节点系统中枢点识别及云聚类分区结果Table 5 Results of pilot nodes identification and cloud clustering partitioning of IEEE 30-bus system

经调整，将分区4整合为分区2，根据式（28）进行无功储备校验，进一步将分区1中无功负荷较重的节点7、21整合到分区2中，经无功校验，此时两分区无功储备裕度分别达到52.96%和30.97%，满足不低于15%的设定要求。表6为IEEE 30节点网络最终分区结果，图3为相应效果图。

表6 IEEE 30节点系统最终分区结果Table 6 Final partitioning results of IEEE 30-bus system

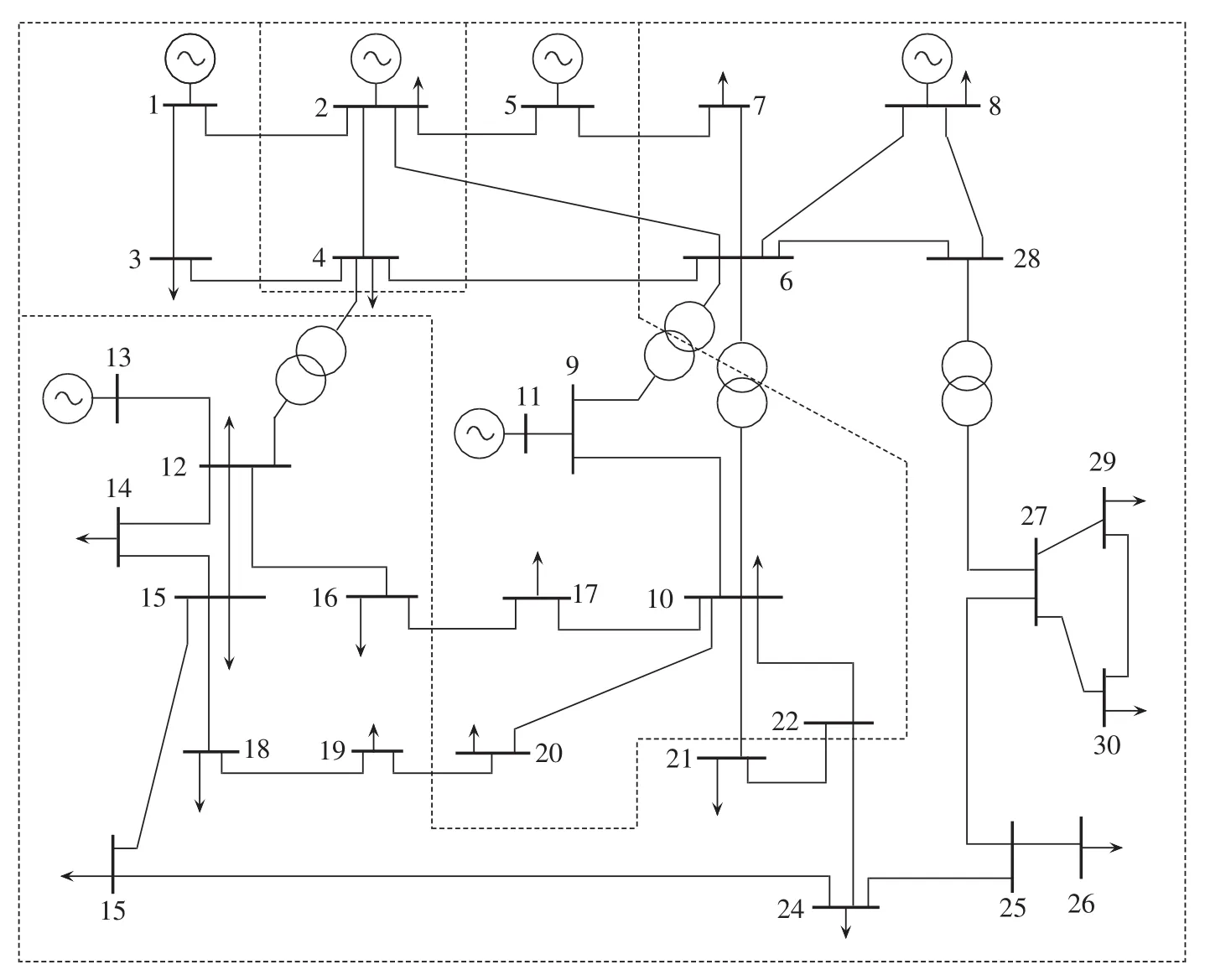
图3 IEEE 30节点输电网络最终分区示意图Fig.3 Schematic diagram of final partitioning results of IEEE 30-bus system

5 结语

本文利用注入电流形式的潮流方程，根据线性灵敏度定性分析，直接通过对全网中枢节点的定量识别，在先确定系统中枢点后以中枢点为无功电压分区中心并引入云模型，建立无功源控制空间，在此基础上由云聚类算法完成所有节点的无功电压分区并进一步整合，对分区结果进行了无功储备裕度校验。通过对IEEE 14、IEEE 30节点系统的仿真测试，验证了所提方法的有效性。