过移相和欠移相对12脉波整流系统的影响及抑制措施

高 蕾，孟凡刚，杨世彦，杨 威

（哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

多脉波整流技术是大功率整流系统抑制输入电流谐波的主要方法，因其具有实现简单、可靠性高和电磁兼容性好等优点而受到越来越多的关注[1]。在多脉波整流系统中，需要使用移相变压器产生几组存在一定相位差的三相电压对整流桥供电，使1个整流桥产生的谐波可以被其他整流桥产生的谐波所抵消，达到抑制输入电流谐波的目的[2-3]。因此，移相变压器是多脉波整流系统的必需器件[4]。

多脉波整流系统所用移相变压器主要分为3类。在输入与输出电压等级差别较大的场合，从安全角度考虑，需要使用隔离式变压器作为移相变压器，如 Y ／△ ／Y[5-6]和△ ／△ ／Y[7-8]型变压器。 隔离变压器的容量约为输出功率的105%，因此，隔离式变压器的使用会增加多脉波整流系统的成本和体积[1]。在只移相而不升降压的场合，可以使用移相电抗器作为移相变压器。由于移相电抗器串联在主电路中，需要的线圈匝数较少，可以显著降低多脉波整流系统的体积和成本[9-10]。然而，由于移相电抗器结构的原因，使用移相电抗器的多脉波整流系统只能降低特征次谐波电流幅值，而不能完全抑制[10-12]。在输入与输出电压相差不大的场合，可以使用多相自耦变压器作为移相变压器[1]。自耦变压器绕组的交互联结形式使得需要通过电磁耦合传递的能量仅为输出功率的很小一部分，且能完全抑制输入电流中的特征次谐波，因此，基于自耦变压器结构的多脉波整流系统在非隔离场合得到了越来越多的应用[13-15]。由于三角形联结自耦变压器能够为三倍频电流提供回路，且其设计合理时容量仅为12脉波整流系统输出功率的18%左右，因此，该类变压器是应用最为广泛的移相变压器[15]。

以12脉波整流系统为例，为抑制输入电流中的特征次谐波，需要使自耦变压器输出的2组三相电压存在30°的相位差，且输出电压幅值相等。当满足该条件时，三角形联结自耦变压器原边绕组与副边绕组的匝比为，该匝比为非整数[15]。因此，在设计自耦变压器时，需要将匝比近似为2个整数的比值。这种近似会使自耦变压器输出的2组三相电压的相位差不再是30°，进而导致系统不能完全抑制输入电流中的特征次谐波。本文定量分析了匝比近似对12脉波整流系统性能的影响，并提出了相应的措施抑制匝比近似导致的非特征次谐波。

1 过移相和欠移相产生原因

图1所示为三角形联结自耦变压器相量图。在图1中，当移相角β大于15°时，称变压器工作于过移相状态；当移相角β小于15°时，称变压器工作于欠移相状态。下面分析过移相和欠移相产生的原因。

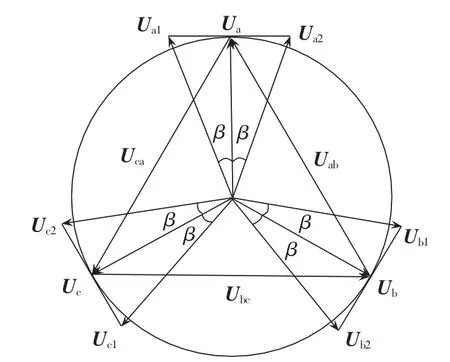
图1 三角形联结自耦变压器的电气量间的关系Fig.1 Relationship among electrical variables of delta-connected autotransformer

图2所示为三角形联结自耦变压器绕组结构图。图2中，Np和Nq分别为原边绕组和副边绕组匝数。

自耦变压器原边绕组和副边绕组匝比定义为：

当移相角β等于15°时，根据相量图可以得到：

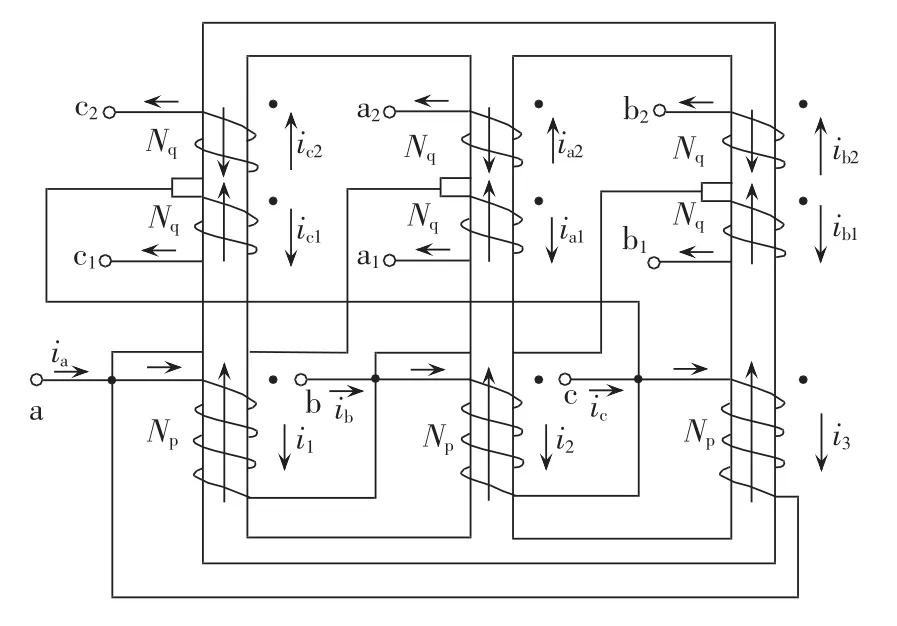
图2 三角形联结自耦变压器绕组结构Fig.2 Winding configuration of delta-connected autotransformer

即：

当原边绕组匝数Np增大，副边绕组匝数Nq保持不变时，匝比k将变大，tanβ 将小于，这会导致移相角β小于15°；类似地，当副边绕组匝数Nq减少，原边绕组匝数Np保持不变时，移相角β也将小于15°。因此，原边绕组匝数增多和副边绕组匝数减少均会使变压器工作于欠移相状态。

当原边绕组匝数Np减小，副边绕组匝数Nq保持不变时，匝比k将变小，tanβ 将大于，这会导致移相角β大于15°；类似地，当副边绕组匝数Nq增大，原边绕组匝数Np保持不变时，移相角β也将大于15°。因此，原边绕组匝数减少和副边绕组匝数增多均会使变压器工作于过移相状态。

2 过移相和欠移相对输入电流的影响

图3所示为使用自耦变压器的12脉波整流系统。图中，零序电流抑制变压器ZSBT（Zero Sequence Blocking Transformer）主要用于抑制三倍频电流形成的零序电流[15]；相间电抗器 IPR（Inter-Phase Reactor）的主要作用是吸收2个整流桥输出电压的瞬时差，保证2个整流桥正常工作。

假设输入电压为：

根据相量图，可以得到自耦变压器输出电压为：

式（5）中的 Um1与式（4）中 Um的关系满足：

在电感负载下，可以得到自耦变压器各相输出电流为：

根据图2和图3，可以得到自耦变压器各相输入电流为：

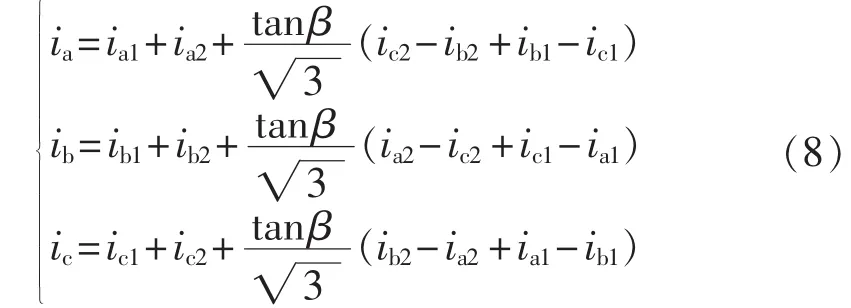
下面以a相为例，分析过移相和欠移相对输入电流的影响。将式（6）和式（7）代入式（8），可以得到a相输入电流的表达式如式（9）所示。

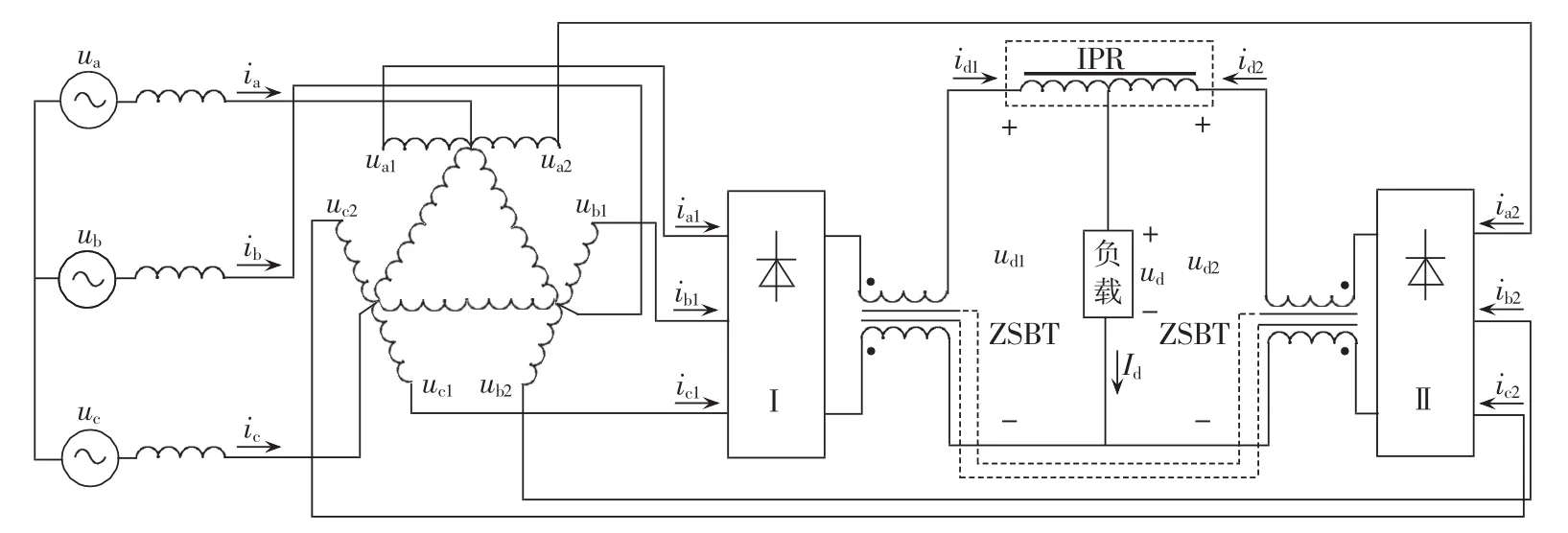
图3 12脉波整流系统Fig.3 12-pulse rectifier system

分析式（9）可知，当 β=15°时，输入电流 ia中不含有 12k±1、12k±2、…、12k±6 次谐波。计算式（9）中的基波电流和各次谐波电流有效值，并将其代入总谐波畸变率（THD）计算公式，得到THD为：

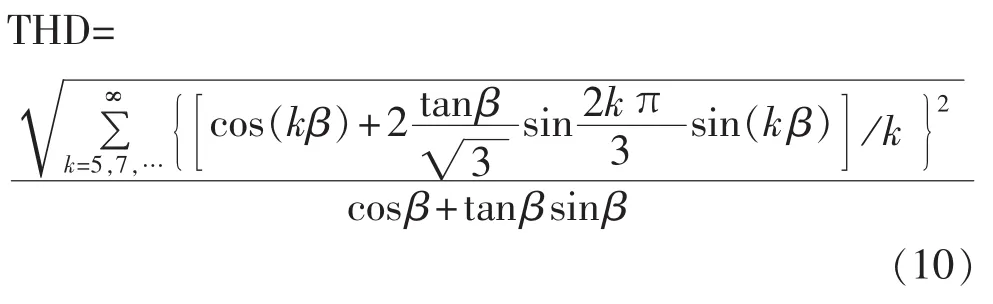
由式（10）可以得到图4所示的移相角与输入电流THD值的关系曲线。从该图可知，当β=15°时，输入电流THD值最小，最小值约为15.22%；无论移相角大于15°还是小于15°，THD值均大于15.22%，这表明无论是过移相还是欠移相均会使输入电流THD值变大；该曲线关于15°对称，这表明过移相相同的角度和欠移相相同的角度对输入电流THD值影响相同。

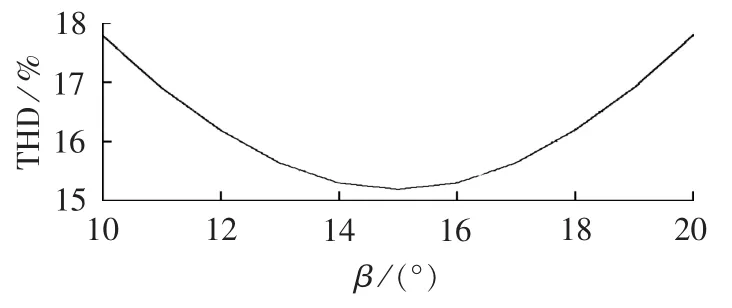
图4 移相角与输入电流THD值的关系Fig.4 Relationship between phase-shift angle and input current THD

根据自耦变压器的相量图，可以得到移相角与原、副边绕组匝数比k的关系为：

根据式（11）可以确定移相角与绕组匝数之间的关系。在MATLAB软件中建立不同移相角时的移相变压器模型，仿真分析了换相角从9°～20°之间的11组不同移相角对12脉波整流系统的影响。仿真时，保持输入电压和负载不变。

图5所示为不同移相角下各次谐波有效值与基波电流的有效值之比 ri（i=5，7，11，13）。 由图 5 可以得到以下结论：随着移相角的增大，5次和7次等非特征次谐波含量先减小后增大；在移相角等于15°时，5次和7次谐波含量近似为0；随着移相角的增大，11次和13次谐波含量先增大后减少；移相角等于15°时，11次和13次谐波含量最大。由于12脉波整流系统中的特征次谐波为12n±1（n为正整数），5次和7次谐波为非特征次谐波，因此，过移相和欠移相会导致输入电流中含有非特征次谐波，并且非特征次谐波的有效值随着移相角偏移15°程度的增大而增大。

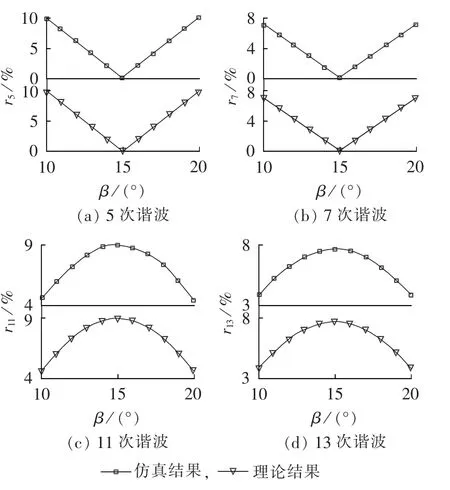
图5 不同移相角下各次谐波与基波电流有效值之比Fig.5 Ratio of harmonic current to fundamental current vs.phase-shift angle for different harmonic orders

3 过移相和欠移相对负载电压的影响

根据调制理论可得2组整流桥的输出电压满足：

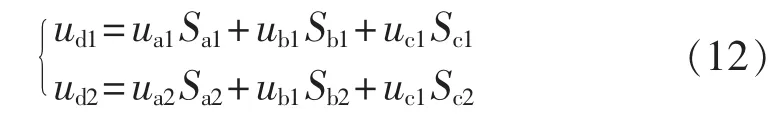
其中，Sa1、Sb1、Sc1、Sa2、Sb2、Sc2分别为 2 组整流桥各相的开关函数。

图6所示为开关函数Sa1。理想条件下，其余各相开关函数与a1相开关函数的关系满足：

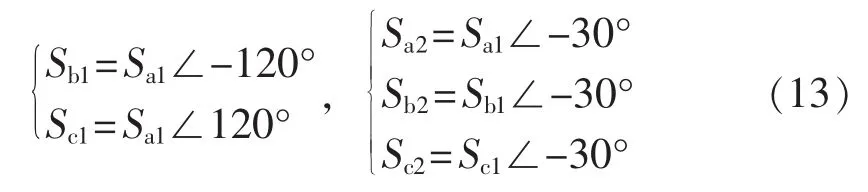
图6 理想状态下a1相开关函数Fig.6 Ideal switching function for phase a1

将式（5）和式（13）代入式（12）可得 2 个整流桥的输出电压为：

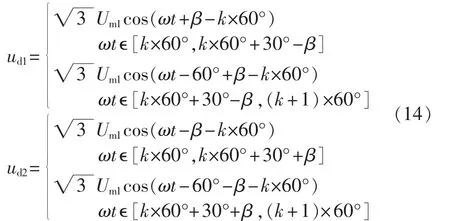
其中，k=0，1，2，…。

由图3可以得到负载电压为：

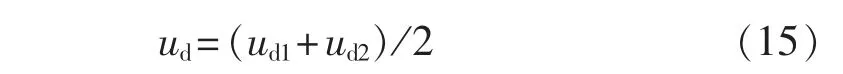
将式（14）代入式（15）得到负载电压为：

定义负载电压纹波系数为：

其中，udmax、udmin和udav分别为负载电压最大值、最小值和平均值。

由式（16）可得 udmax、udmin和 udav分别为：

将式（18）代入式（17），可以得到负载电压纹波系数与移相角的关系，如式（19）所示。

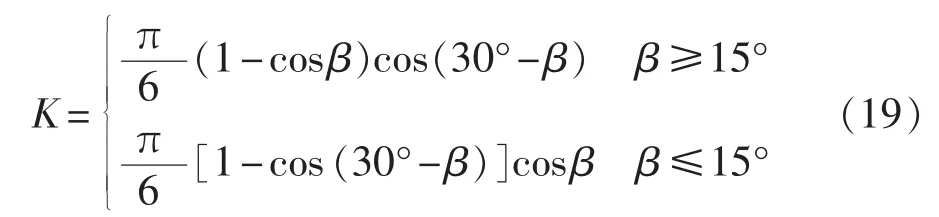
图7 移相角与负载电压纹波系数关系Fig.7 Relation between phase-shift angle and voltage ripple coefficient

根据式（19）可以绘制移相角与负载电压纹波系数的关系曲线，如图7所示。由图7可知，负载电压纹波系数与移相角的关系和输入电流THD值与移相角的关系类似，当且仅当移相角等于15°时，纹波系数最小，即无论是过移相还是欠移相都会使纹波系数增大。

4 过移相和欠移相抑制措施研究

在文献[16]中，Dudi.A.Rendusara 等分析了谐波抑制电抗器HBR（Harmonic Blocking Reactor）对输入电压不平衡的抑制作用，并将其应用于分别使用△／Y／△变压器和三角形联结自耦变压器的整流系统；文献[17]对其进行了扩展，将其应用于使用多边形自耦变压器的六相整流系统。在文献[16-17]中，HBR的主要作用是抑制输入电压不平衡导致的非特征次谐波。由于过移相和欠移相都会导致非特征次谐波的产生，为此，本节将在文献[16-17]的基础上，分析HBR的绕组可行性布置方案，通过计算各相HBR压降和HBR对各次谐波的阻抗，寻找HBR最优结构，并将该最优结构应用于抑制过移相和欠移相产生的非特征次谐波。图8所示为文献[16]给出的使用HBR的12脉波整流系统，图9所示为HBR的第3个芯柱绕组结构图。

根据图9可以得到该芯柱的磁动势方程为：

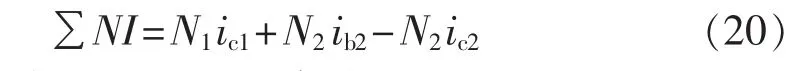
图10所示为各相电流基波磁通抵消相量图。

事实上，当自耦变压器移相角为π／2时，HBR的绕组结构有多种布置方案。从保证系统对称性和HBR结构最简角度出发，图11给出了其中的12种方案。在这12种方案中，方案1和方案9中谐波抑制电抗器匝数比满足，其余各方案中匝数比满足

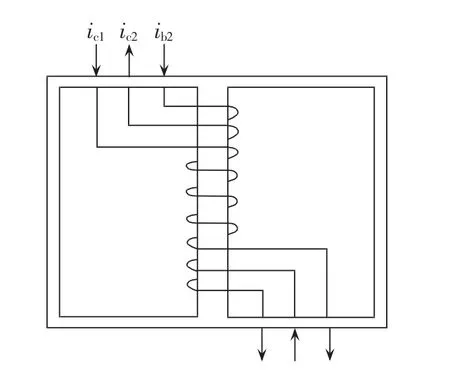
图9 HBR绕组结构图Fig.9 Winding configuration of HBR

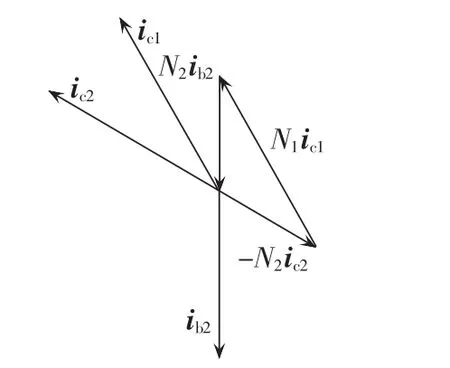
图10 各相基波电流和磁通相量图Fig.10 Phasor diagram of fundamental phase currents and fluxes

对于谐波抑制电抗器，线圈电感与匝数的平方成正比，即在方案1和方案9中绕组电感满足：

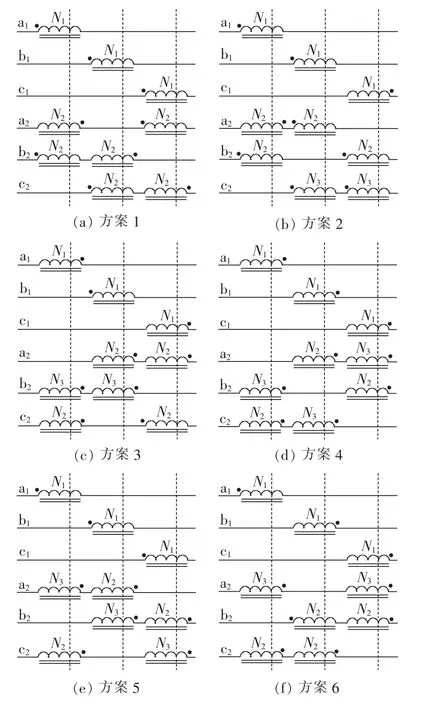
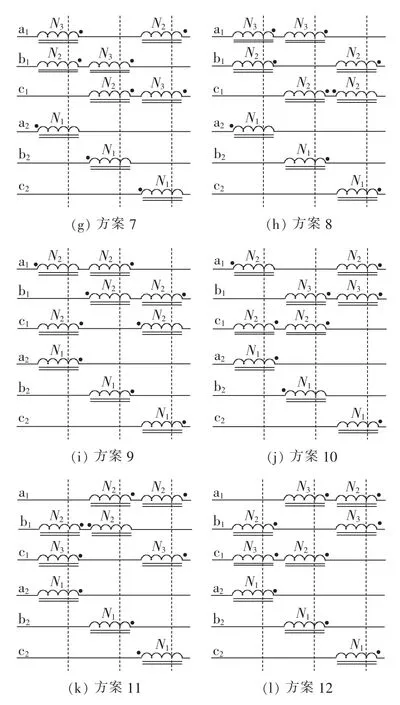
图11 HBR绕组布置方案Fig.11 Winding configuration schemes of HBR

其余方案中绕组电感满足：

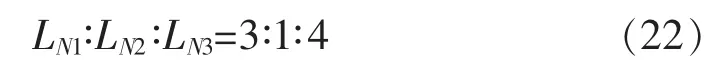
根据式（21）、式（22）和欧姆定律，可以得到各相所接入的HBR压降（归一化值）比较，如表1所示。表1中，kc为耦合系数。

分析表 1可知，方案 2、方案3、方案 6、方案 8、方案10和方案11中的HBR压降均不相等，不相等的压降可能会加剧系统的不对称，因此这6种方案不适合实际应用；方案1和方案9中各相谐波抑制电抗器压降有效值近似相等，因此这2种方案对称性最好。

HBR的本质是使基波电流产生的磁通为0，谐波电流产生的磁通不为0，即对基波电流表现为零阻抗，而对谐波电流表现为高阻抗。表2所示为方案1、方案 4、方案 5、方案 7、方案 9、方案 12对各次谐波的阻抗（归一化值）。

对比表2所示的各次谐波阻抗可以得到，方案7的5次和7次谐波阻抗有效值要小于其他5种方案，而其他5种方案的5次和7次谐波阻抗有效值相等。考虑到过移相和欠移相主要会产生5次和7次非特征次谐波，同时考虑HBR的对称性，方案1和方案9为最优方案。

表1 各相所接HBR压降有效值比较Table 1 Comparison of RMS of HBR voltage drop among different phases for different schemes

表2 各方案谐波阻抗比较Table 2 Comparison of harmonic resistance among different schemes

5 仿真与实验验证

分析表2可以得到，方案1和方案9所示的HBR对三倍频谐波具有一定的抑制作用，而图3中ZSBT的作用是抑制三倍频电流，因此，当使用HBR后，12脉波整流系统可以不使用ZSBT，结构如图12所示。相对于图10所示的整流系统，图12所示系统仅使用1个IPR，可有效减少系统磁性器件容量。HBR结构采用方案1。

为仿真和实验验证移相角对12脉波整流系统的影响，以及HBR对于过移相和欠移相的抑制作用，设计了3个不同匝比的三角形联结自耦变压器。3个变压器的匝比分别为 5、6.5、8，根据式（11）可得移相角分别为 19.1°、14.92°、12.22°。

仿真和实验时，系统输入线电压为250 V，负载电阻为25 Ω，电感为10 mH。

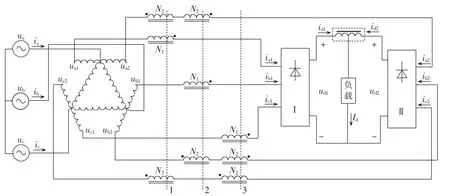
图12 由HBR和单IPR构成的12脉波整流系统Fig.12 12-pulse rectifier system composed of one HBR and one IPR

图13和图14所示分别为未采用HBR时系统输入电流的仿真和实验结果。由图13和图14可知，未采用HBR时，过移相和欠移相均会导致输入电流中含有5次和7次非特征次谐波，且输入电流THD值较大。仿真和实验时，由于自耦变压器、HBR及IPR漏感的影响，当匝比为6.5时，输入电流THD值小于其理论值，甚至比移相角为15°时的输入电流THD理论值还要小。

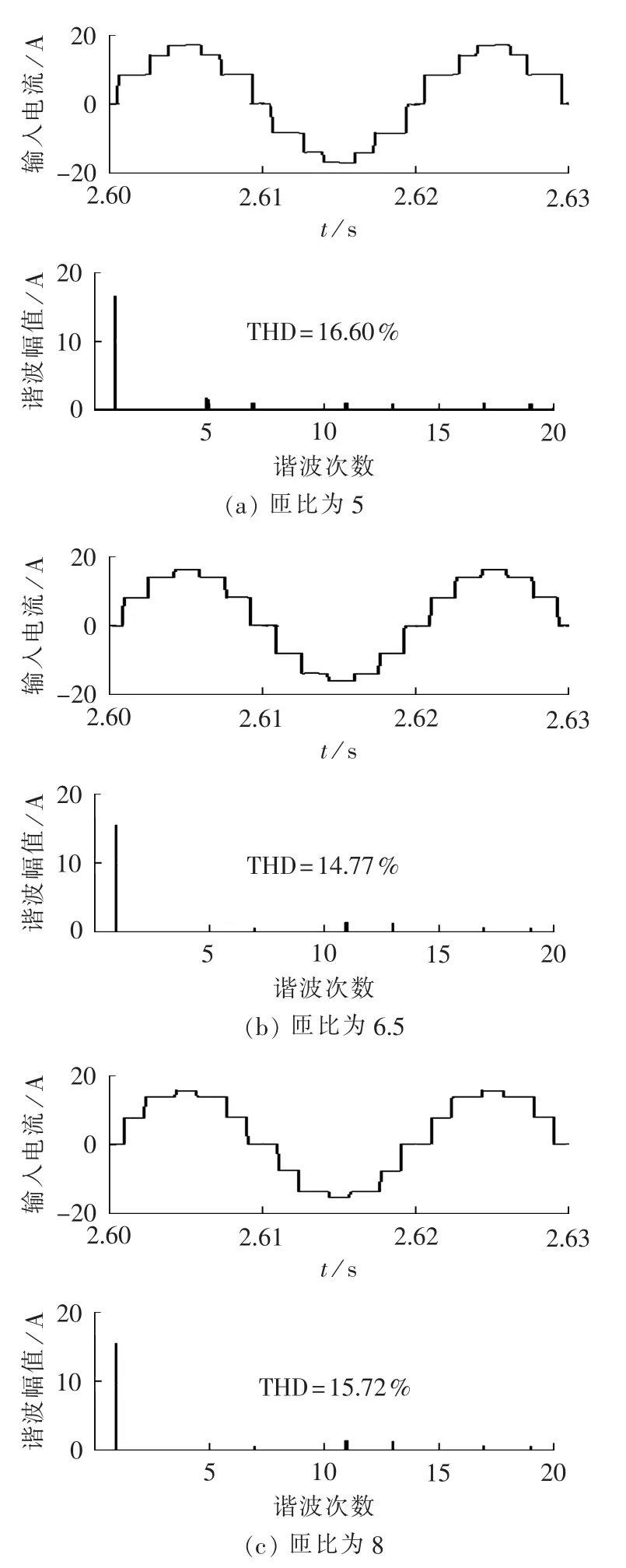
图13 未采用HBR时，不同匝比下12脉波整流系统输入电流、谐波电流及THD的仿真结果Fig.13 Simulative input current，harmonic current and THD of 12-pulse rectifier system without HBR for different turn-ratios

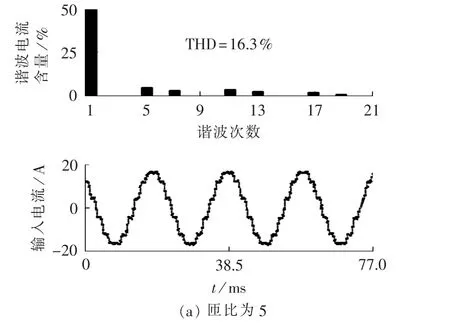
图14 未采用HBR时，不同匝比下12脉波整流系统输入电流、谐波电流及THD的实验结果Fig.14 Experimental input current，harmonic current and THD of 12-pulse rectifier system without HBR for different turn-ratios

图15和图16所示分别为使用HBR时系统输入电流的仿真和实验结果。由图15和图16可知，使用HBR后，输入电流中的5次和7次谐波得到了显著抑制，并且输入电流THD值较未采用HBR时要小。

因此，采用HBR可以有效降低输入电流的THD值，抑制输入电流中的非特征次谐波。

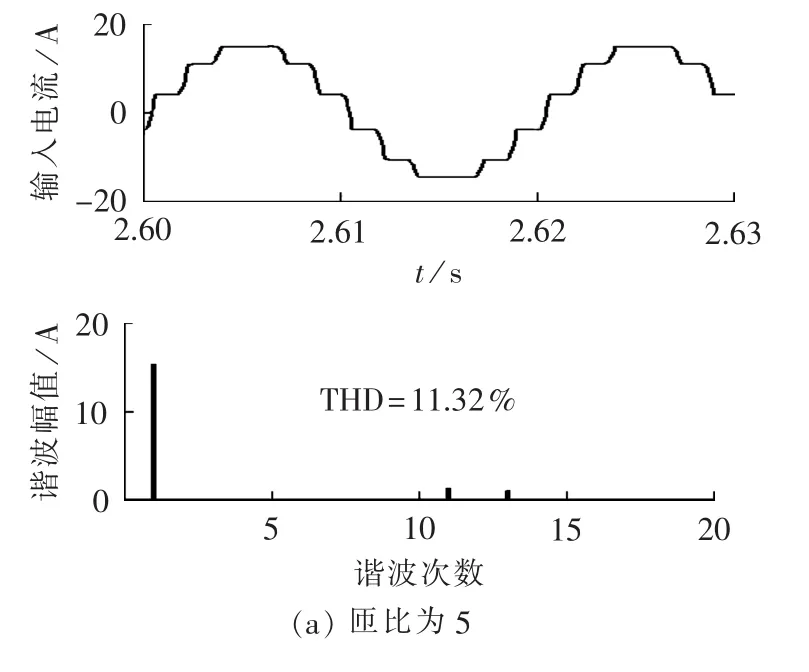
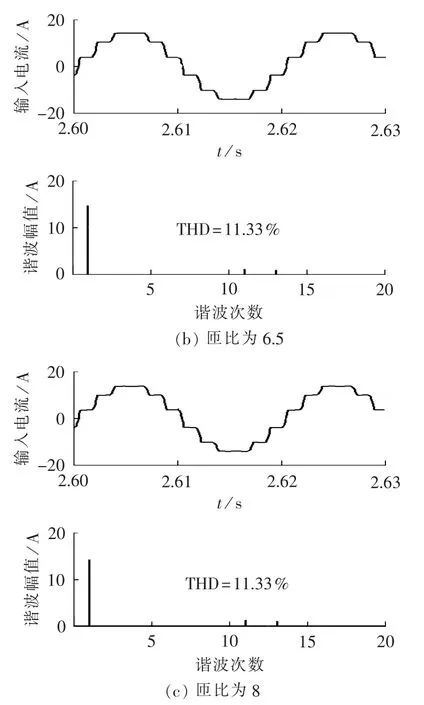
图15 采用HBR时，不同匝比下12脉波整流系统输入电流、谐波电流及THD的仿真结果Fig.15 Simulative input current，harmonic current and THD of 12-pulse rectifier system with HBR for different turn-ratios

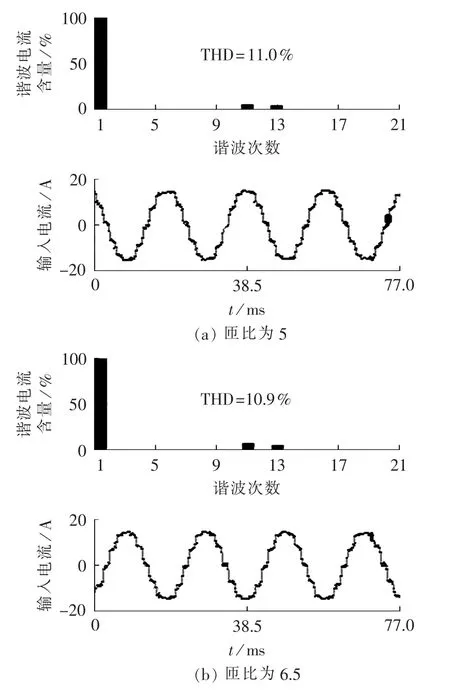
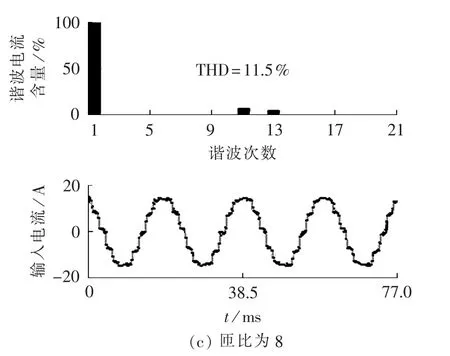
图16 采用HBR时，不同匝比下12脉波整流系统输入电流、谐波电流及THD的实验结果Fig.16 Experimental input current，harmonic current and THD of 12-pulse rectifier system with HBR for different turn-ratios

6 结论

本文定量分析了自耦变压器过移相和欠移相对12脉波整流系统的影响，并提出了一种应用HBR抑制过移相和欠移相导致的非特征次谐波的方法。得到的结论如下：

a.过移相和欠移相都会使输入电流中含有非特征次谐波，并增大输入电流THD值和负载电压纹波系数；

b.可以使用HBR抑制过移相和欠移相产生的非特征次谐波；

c.HBR对三倍频电流具有抑制作用，可代替ZSBT；

d.提出了HBR和单IPR相结合的12脉波整流系统，在抑制输入电流非特征次谐波的同时，有效降低了系统磁性器件容量；

e.本文所提出的12脉波整流系统不仅能够抑制过移相和欠移相所导致的非特征次谐波，还可以用来抑制输入电压不平衡和系统结构不对称所产生的非特征次谐波。