考虑运行功率变化影响的风电变流器可靠性评估
2015-09-19季海婷陈耀君刘盛权胡姚刚唐显虎
李 辉 ,季海婷 ,秦 星 ,陈耀君 ,刘盛权 ,胡姚刚 ,冉 立 ,唐显虎
(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.重庆科凯前卫风电设备有限责任公司,重庆 401121)
0 引言
风电变流器是风电机组中的核心部件,是控制风电机组输出功率至电网的重要环节,其故障可能导致整个系统运行中断,甚至是重大的安全事故和经济损失[1-5]。由于风速的不稳定性、运行环境恶劣等原因,相比于一般工业用变流器,风电用变流器输出功率随机变化性大,具有不稳定性的特点,其可靠性明显低于一般工业用变流器[6-7]。研究表明,由于结温大小和波动强度的变化,变流器各功率器件的铝键合线和焊料层承受长期、频繁的膨胀收缩,导致不均衡电热应力的产生,造成疲劳累积,这是功率器件铝键合线断裂和焊料层开裂的根本原因[8-9]。目前,直接监测器件的结温变化在工程上不容易实现,现在主要采用等效热阻网络,根据外部可监测数据进行计算。由于风电变流器的运行功率大小直接与功率器件的结温大小相关,变流器运行功率的波动强度与功率器件的结温波动强度有关。因此,如何考虑功率大小和功率波动强度的双重因素,准确地反映输出功率随机变化对器件结温大小和结温波动的影响,结合实际风电场中一年内的运行数据记录,提出一种工程上容易实现的变流器可靠性评估方法,对于制定合理的风电场运行维护策略有重要意义。
目前,国内外研究中,已有部分文献从电力电子器件的失效模式出发,研究变流器的可靠性[10-13]。如文献[11]采用功率循环曲线建立结温与功率循环能力的关系,采用实际风电运行数据对不同结温均值、结温波动下IGBT的功率循环能力进行了统计研究,但仅采用统计的方法,没有考虑功率大小和功率波动强度对IGBT可靠性的影响;文献[12-13]根据Arrhanius关系式推导,建立了风电机组变流器电子元器件故障率与结温变化的关系,并分析了最大出力状态下电子元器件故障率随运行时间的变化,但仅在最大出力状态下进行分析,没有考虑风电变流器输出功率随机变化对结温的影响。虽然文献[14]根据FIDES可靠性评估导则,建立了元器件故障率与结温的关系,考虑了风电变流器输出功率对结温的影响,但只针对输出功率大小对可靠性影响进行分析,且在提取元器件所承受的随机载荷信息时处理过于简单。
基于此,为了充分考虑运行功率随机变化对变流器可靠性评估的影响,本文提出一种考虑功率大小和功率波动强度因素的变流器可靠性评估多状态模型。首先,将功率大小和功率波动强度作为变流器运行状态的二维划分因素,以热应力因子和温度循环因子来衡量结温大小和结温波动对故障率的影响,建立变流器元器件故障率的统一计算模型;其次,结合器件结温计算方法获取器件结温载荷历程,并通过雨流计数法获取载荷波动信息,建立风电变流器子系统级的可靠性多状态概率评估模型;最后,以某风电场实际监测数据为例,分析所建评估模型的收敛性并评估风电变流器子系统的故障率,并进一步分析功率大小和功率波动强度对器件结温均值和结温波动的分布以及故障率评估的影响。
1 风电变流器元器件故障率统一计算模型
1.1 风电变流器运行工况的二维状态划分
考虑功率大小和功率波动强度可能导致风电变流器的元器件承受不均衡的电热应力,从而影响对其可靠性的准确性评估,本节基于多状态概率分析法[15]建立表征功率大小和波动强度影响因素的变流器二维状态概率模型:

其中,p(i,j)表示变流器处于功率大小为第 i个状态、功率波动强度为第 j个状态(S(i,j))下的概率;t(i,j)表示变流器处于 S(i,j)状态下的累计时间;T为计及的运行周期;NTh为功率大小划分的状态数;NCy为功率波动强度划分的状态数。
功率波动强度定义为:

其中,Pmean为功率平均值;σ为功率标准差。
1.2 变流器元器件故障率统一计算模型
为了衡量结温大小和结温波动对变流器元器件故障率的影响,本文以热应力因子和温度循环因子作为衡量因子。根据FIDES导则[16],变流器处于功率大小为第i个状态下的元器件热应力因子可以统一表示为:
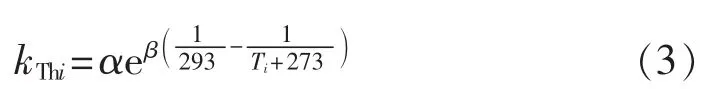
其中,α、β均为常数,不同元器件对应的具体数值不同;Ti为每个运行状态下的温度参数,其中对应IGBT和二极管为结温,对应电容和电感为电路板平均温度。
变流器处于功率波动强度为第j个状态下的元器件温度循环因子可以统一表示为[16]:

其中,tj为元器件处于每个运行状态下的累计运行时间,单位为h;NCyj为元器件在每个运行状态下的结温循环波动次数;N0为参考循环波动次数,一般取值为2;θCyj为元器件每个运行状态下的结温波动循环时间;θ0为参考循环时间,一般取值为12;ΔTCyj为元器件每个运行状态下的结温波动幅值;Tmax_Cyj为元器件每个运行状态下结温波动所达到的最大值;γ、p、n为不同元器件的调整系数。
考虑到影响风电变流器元器件负荷水平的因素中不仅包括变流器输出功率大小而且包括功率的波动,因此本文在前述对变流器运行工况进行二维状态划分的基础上,结合热应力因子和温度循环因子[16],建立变流器元器件故障率的统一计算模型为:
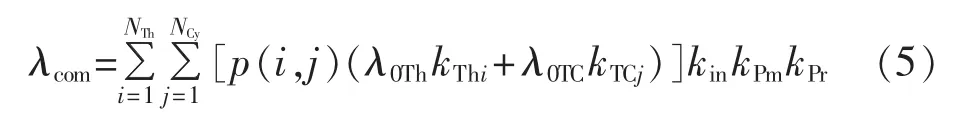
其中,λ0Th和λ0TC分别为热应力因子和温度循环因子对应的元器件基本故障率;kPm表征元器件制造质量的影响;kPr表征元器件寿命周期中的可靠性质量管理及控制水平的影响;kin表示元器件的过应力贡献因子。
2 风电变流器可靠性评估模型
2.1 变流器元器件的结温计算
本文以双PWM方式的IGBT和二极管的损耗和结温计算为例,来说明本文建立变流器可靠性的评估模型及流程。IGBT和二极管的导通损耗为[17-18]:

将导通损耗和开关损耗相加即可得到IGBT和二极管的总损耗。其中,Eon、Eoff分别为IGBT的额定导通和关断能量损耗;Erec为二极管的额定反向恢复损耗;rCE、rD分别为IGBT和二极管的导通电阻,UCE0、Uf0分别为IGBT的导通阈值电压和二极管的额定正向压降,Uref,T、Iref,T、Uref,D、Iref,D分别为IGBT和二极管的额定电压和额定电流,这些参数可以从相应的器件参考手册中查到;fsw为变流器的开关频率,M为PWM的调制系数,cos α为机侧或网侧的功率因数,Iom为变流器相电流幅值,Udc为变流器直流侧额定电压,这些参数可以根据SCADA记录数据得到。
IGBT和二极管的热阻模型[18]如图1所示。

图1 IGBT和二极管热阻等效模型Fig.1 Thermal resistance equivalent model for IGBT and diode
图中,Ta、Tc和Th分别为环境温度、散热器温度和基板温度;Tj,T和Tj,D分别为IGBT和二极管的结温;Rthch和Rthha分别为基板到散热器和散热器到环境的热阻;Rthjc,T和 Rthjc,D分别为 IGBT 和二极管的结点到基板的热阻;PT和PD分别为单个IGBT和二极管的损耗。Ploss为IGBT和二极管封装的总损耗,根据具体的封装形式,相应的损耗可由式(6)—(9)计算得出。则IGBT和二极管的结温计算公式为:
此外,对于变流器中滤波电容、电感、接触器、开关等器件,其损耗、温度的计算方式可以参考文献[17-20]。
2.2 基于监测数据的风电变流器可靠性评估流程
风电场SCADA数据能实时记录风电机组运行工况,为变流器的可靠性评估提供有用信息。本文选取的SCADA数据记录尺度为1 min,与可靠性评估相关的信息项包括变流器有功功率、变流器无功功率、变流器线电流、变流器线电压和变流器柜内温度。
基于历史监测数据的风电变流器可靠性评估流程如图2所示,其中风电变流器按可靠性功能划分为6个子系统,分别为机侧变流器、网侧变流器、直流环节、滤波器、控制系统和附属连接设备[21]。可靠性评估的具体步骤如下。
a.对变流器的运行工况进行二维状态划分。
首先,将变流器输出的有功功率以每小时为一组(每组 60 个数据),按照式(1)、(2)将每小时的平均功率和功率波动强度进行二维状态划分,平均功率大小划分的状态数为NTh,功率波动强度划分的状态数为NCy,即根据变流器的功率大小和波动状态得到变流器运行工况的二维状态划分 S(i,j);其次,计算每个二维状态 S(i,j)下对应的分布概率 p(i,j),并将每个记录时间点对应的变流器有功功率、变流器无功功率、变流器线电流、变流器线电压和变流器柜内温度按照状态 S(i,j)进行归类,形成状态 S(i,j)下的数据集合 Ω(i,j)。
b.计算不同运行工况下元器件结温均值和结温波动。
将状态S(i,j)下每个时间记录点的数据集合Ω(i,j)按元器件的损耗计算公式和热阻模型,对其进行整合计算,得出元器件在运行状态S(i,j)下每小时的结温载荷历程。风电功率的不稳定性导致器件结温的时间历程复杂。因此,需要一种符合材料疲劳累积规律的统计方法,将随机载荷转化为不同恒幅载荷构成的变幅载荷。雨流计数法符合材料的应力-应变规律,故采用雨流计数法提取元器件每小时的温度载荷循环均值、幅值、次数和循环持续时间,并将这些信息按照不同运行状态S(i,j)求平均值。最后,根据式(3)、(4)计算元器件在功率大小为第 i个状态下的热应力因子kThi和功率波动强度为第j个状态下的温度循环因子kTCj。
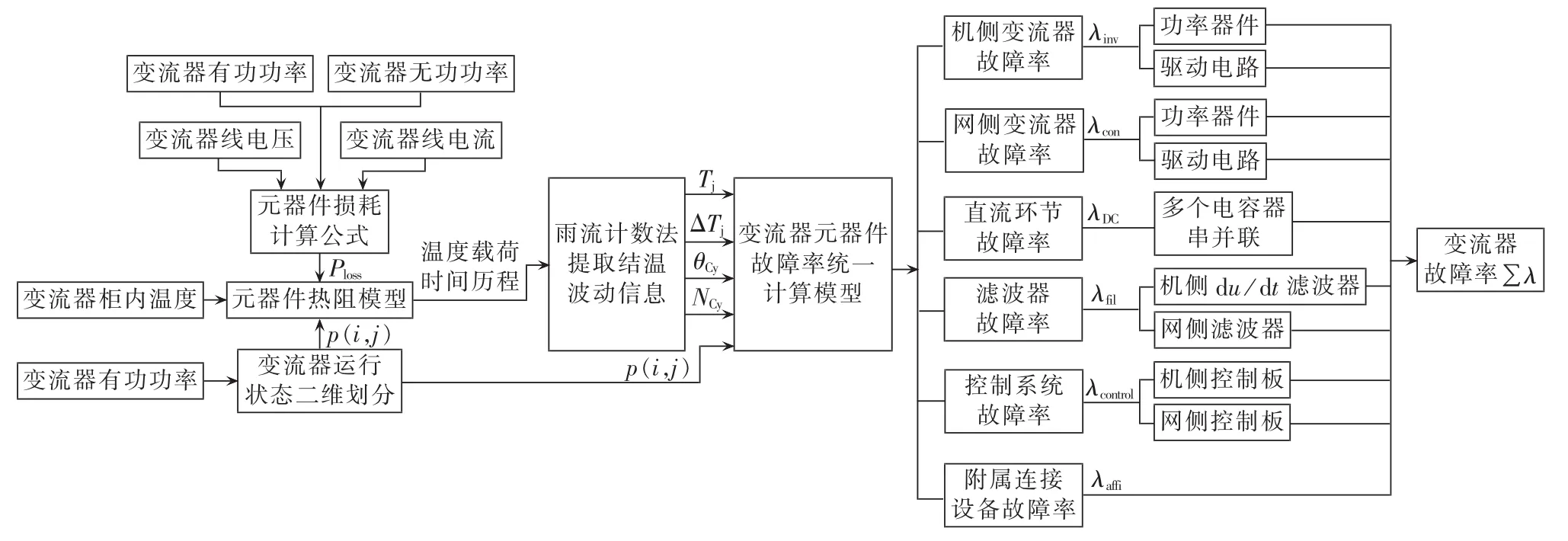
图2 基于SCADA信息的风电变流器系统级可靠性评估框图Fig.2 Block diagram of system reliability evaluation based on SCADA information for wind power converter
c.计算变流器故障率。
根据热应力因子和温度循环因子的计算结果,结合不同元器件的基本故障率参数λ0Th和λ0TC,按照式(5)计算各元器件的故障率;并按变流器可靠性功能子系统划分结构,将不同子系统的故障率相加,得到变流器系统级故障率。
3 实例分析
为了说明本文所提出的评估模型的有效性,并验证其更能准确反映结温大小和结温波动的变化,本节以某风电场某台2 MW永磁同步机组一年内实际记录的SCADA信息为例对变流器可靠性进行评估,并与现有文献中所提出的只考虑功率大小的评估方法进行对比[14]。
变流器功率器件IGBT和二极管的可靠性参数[16]:IGBT 型号 FZ2400-R17KE3;IGBT 额定电压 Uref,T为1700 V;IGBT 额定电流 Iref,T为 2400 A;IGBT 额定饱和压降 UCEsat为 1.9 V;IGBT额定导通压降 UCE0为1.54 V;二极管额定正向压降Uf0为0.81 V;IGBT导通关断损耗Eon+Eoff为1 070 mJ;二极管反向恢复损耗Erec为390 mJ;IGBT结点到散热器的热阻为19 K/kW;二极管结点到散热器的热阻为44 K/kW;散热器到环境的热阻为0.454 K/kW;封装形式为ISOTOP;热应力参数α为1;热应力参数β为0.7;IGBT热应力基本故障率λ0TC为0.302 1;二极管热应力基本故障率λ0TC为0.157 4;温度循环参数γ为1.4;温度循环参数pcase为0;温度循环参数psolder为1/3;温度循环参数 ncase为4;温度循环参数 nsolder为1.9;温度循环基本故障率λ0TC_case为0.033 33;温度循环基本故障率λ0TC_joint为0.1665;元件的制造质量的影响kPm为0.75;元件寿命周期中的可靠性质量管理及控制水平的影响kPr为4;过应力贡献因子kin为3。
变流器直流侧滤波电容的可靠性参数[16]:型号EPCOS_B43458;电容大小为 4700 μF;额定电压为450V;等效串联电阻为25mΩ;基本尺寸为76.9 mm×118.2 mm;热应力参数α为0.85;热应力参数β为4641.6;热应力基本故障率λ0TC为0.4;温度循环参数γ为0.14;温度循环参数p为1/3;温度循环参数n为1.9;温度循环基本故障率λ0TC为0.4。
变流器其他子系统故障率取值[21]:网侧滤波器、机侧滤波器都为0.0056064次/a;功率器件驱动电路为0.0324996次/a;功率连接器、光缆等附属设备为0.0128772次/a;网侧控制板和机侧控制板都为0.1327140次/a。
考虑篇幅限制,本节仅计算机侧、网侧功率模块和直流环节子系统的故障率,其他子系统的故障率则采用文献[21]所提供的数据。变流器额定运行参数:切入风速为3 m/s;额定风速为11 m/s;切出风速为25 m/s;电网电压为690 V;功率器件开关频率为2 kHz;机侧变流器额定电压为690 V;直流侧额定电压为1100 V。
该风电场2009年4月26日到2010年4月26日一年内的风速和变流器输出有功功率的概率密度分布如图3所示。
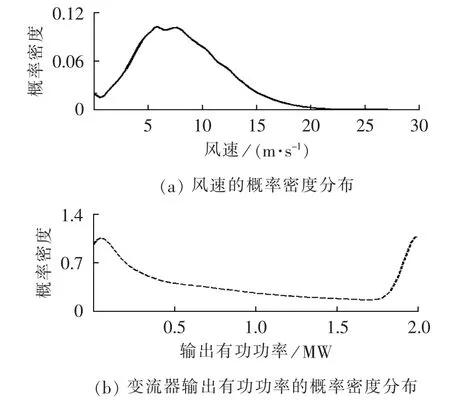
图3 某风电场风速、变流器输出有功功率的概率密度分布Fig.3 Probability density distribution for wind speed and converter output active power of a wind farm
由图3可见,该风电场的风速集中分布在切入风速3 m/s和额定风速11 m/s之间。变流器的输出有功功率集中分布在零出力和额定出力两点上,中间部分随输出功率的增大逐步减小。按照本文所提出的方法,则变流器的运行工况按输出功率大小和功率波动强度进行二维状态划分的结果如图4所示。
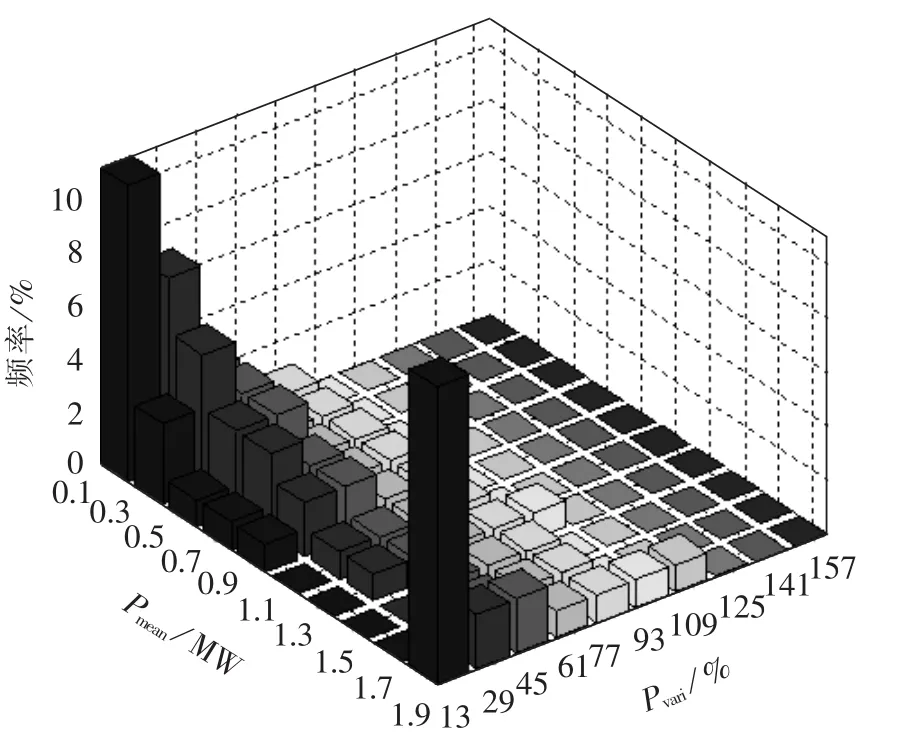
图4 风电变流器运行功率的二维状态划分Fig.4 2-D state allocation of operational power of wind power converter
由图4可见,变流器一年内的输出功率大小在最小值和额定值分布最多,中间部分随输出功率的增大分布逐步减少。此外,该风电场机组的变流器一年内的输出功率波动强度主要集中在13%~77%,且随着功率波动强度的增加,分布频率逐步减少。
为了分析不同状态数对变流器可靠性评估的影响,说明本文所提出方法的收敛性,采用不同状态数对上述风电场的变流器可靠性进行评估,所得结果如表1所示。由表1可以看出,随着选取的状态数增加,利用本文所建立的评估模型计算的故障率将逐步趋于稳定,说明本文建立的评估模型具有收敛性。当状态数选取大于18×18时,得到了该风电机组评估变流器故障率值稳定在0.478次 /a,其中,机侧功率模块的故障率为0.096次 /a,网侧功率模块的故障率为 0.060 3次/a,直流环节的故障率为0.000365次/a,其评估结果与实际统计情况相一致,即机侧变流器比网侧变流器更容易出现故障[7]。与文献[21]的评估结果相比,即PWM控制的功率变流器中,其功率模块的故障率为0.0878次/a、直流环节的故障率为0.000464次/a在数量级上相一致,进一步证明了本文所建立的变流器可靠性评估模型的有效性。
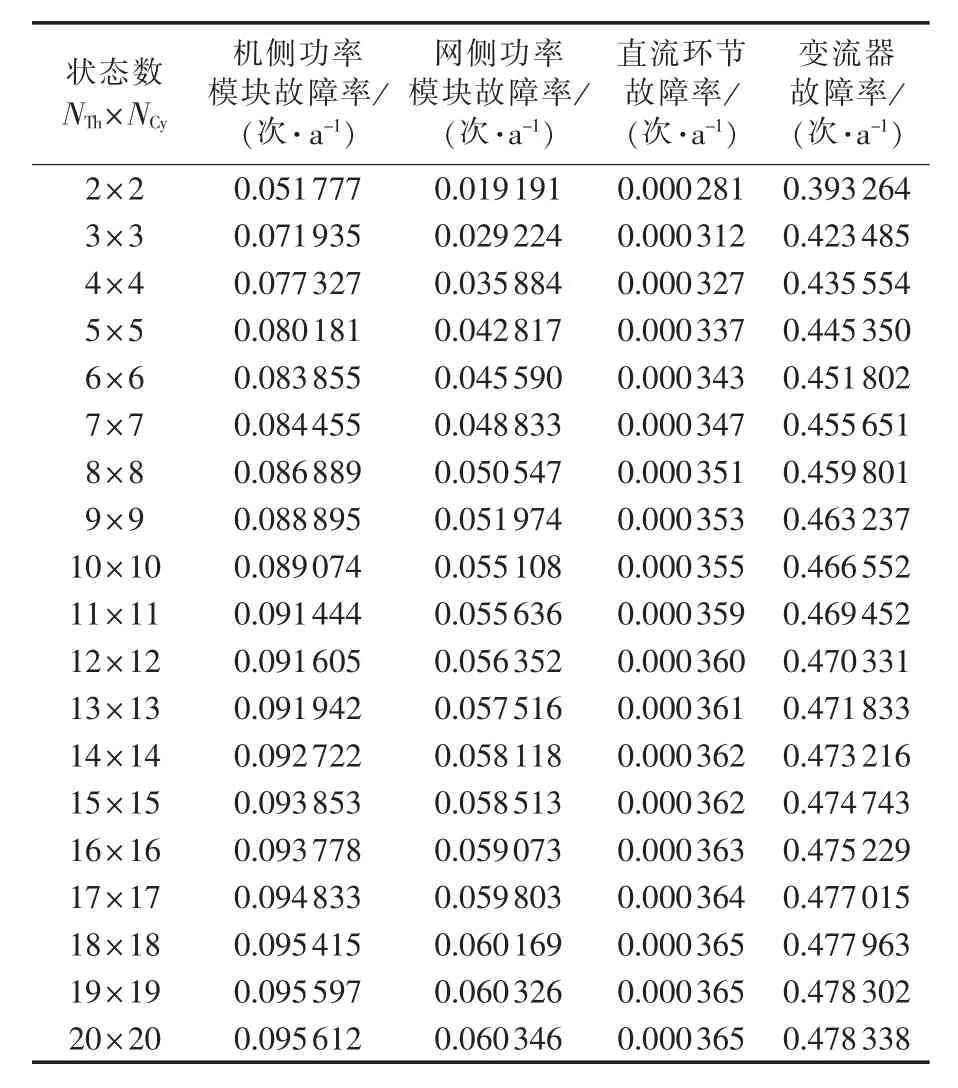
表1 不同状态划分数下变流器的故障率评估结果Table 1 Results of converter failure rate evaluation for different state allocation numbers
为了进一步分析本文所提出的评估模型和方法的有效性,将不同状态数下本文计算的故障率结果与现有文献只考虑功率大小的评估结果进行对比,如图5所示。由图5可以看出,当状态数达到一定程度时,2种评估模型都具有收敛性,且评估的机侧功率模块故障率都比网侧功率模块故障率大。但是,由于本文建立的评估模型同时考虑功率大小和功率波动强度的影响,因此可以看出,当评估结果趋于稳定时,无论是机侧、网侧功率模块还是直流侧电容,采用本文方法所得的故障率评估结果都比仅考虑功率大小方法的评估结果大。这进一步说明,与本文建立的评估模型结果相比较,仅考虑功率大小评估方法的故障率计算结果比较乐观。

图5 不同评估方法变流器可靠性评估结果对比Fig.5 Comparison of converter reliability evaluation results between different evaluation methods
4 功率大小和功率波动强度对可靠性评估的影响
4.1 功率变化对机侧IGBT结温分布的影响
为了分析本文所提出的评估模型和方法更能准确反映变流器器件结温大小和结温波动的变化,从而验证变流器可靠性评估中考虑功率大小和功率波动强度的必要性。本节以机侧IGBT为例,分析功率大小和波动强度对其结温分布的影响。
为了分析变流器功率大小和功率波动强度对变流器元器件结温变化的影响规律,本文将上述风电场变流器输出有功功率的原始数据做如下处理:保持每小时功率波动强度不变,将每个数据点同时增大或者减少,改变平均功率大小;保持每小时平均功率不变,将每个数据点围绕均值进行同比例放大或缩小,改变功率波动强度。考虑到额定功率的限制,上述数据处理中每个功率点都限幅在2 MW以内。该风电场原始变流器输出功率的平均值为1.0 MW,功率波动强度为85%。根据第2.2节所述评估流程,可以计算出功率器件结温均值和结温波动的分布。图6为功率波动强度保持85%不变,平均功率大小变化时对机侧IGBT结温分布的影响。图7为平均功率大小保持1.0 MW不变,功率波动强度变化时对变流器机侧IGBT结温分布的影响。图中,Tjm为结温均值;TjD为结温波动。
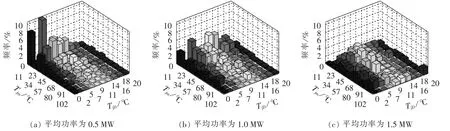
图6 功率波动强度保持85%不变,不同平均功率下风电变流器机侧IGBT结温分布Fig.6 Junction temperature distribution of wind power converter generator-side IGBT for different average powers with same power fluctuation of 85%
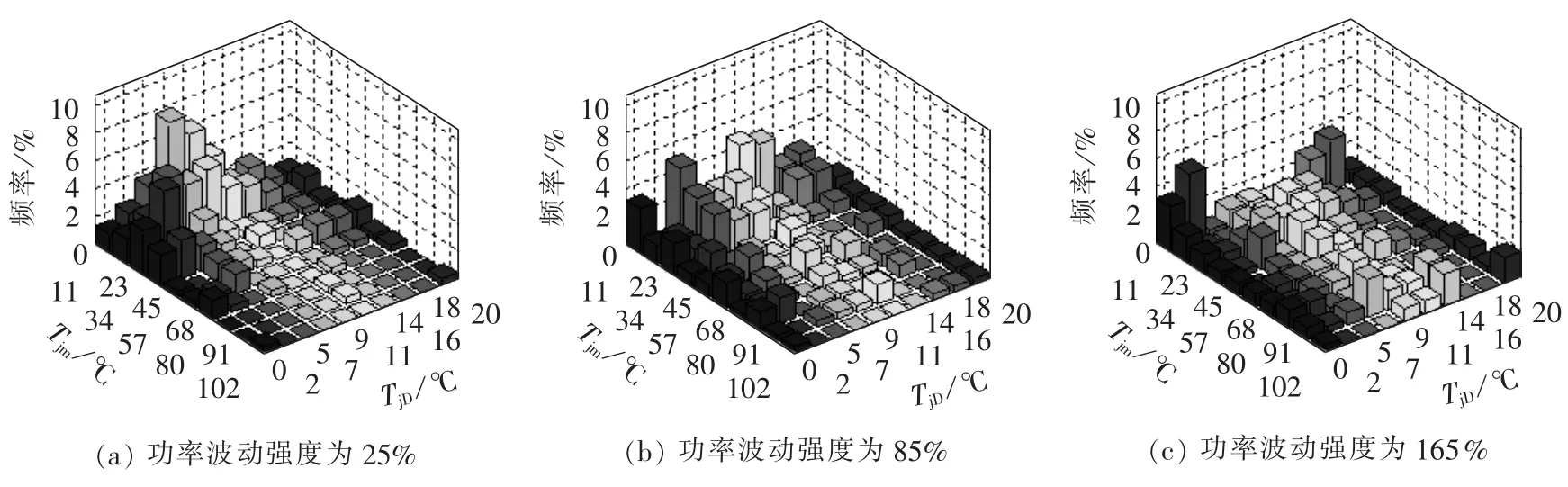
图7 平均功率保持1.0 MW不变,不同功率波动强度下风电变流器机侧IGBT结温分布Fig.7 Junction temperature distribution of wind power converter generator-side IGBT for different power fluctuations with same average power of 1.0 MW
通过图6和图7的比较可以看出,随着功率大小和功率波动强度的增加,机侧IGBT的结温均值和结温波动的频率都在增大。由图7还可以看出,当平均功率大小保持1.0 MW不变时,不同功率波动强度的变化同样会引起较大幅度的IGBT结温均值和结温波动的变化,从而对可靠性评估结果造成影响。在平均功率保持1.0 MW不变的情况下,当功率波动强度分别为25%、85%、165%时,由图7可知,机侧IGBT一年内承受不同结温均值和结温波动的分布频率不同,从而造成故障率评估结果的差异,机侧IGBT的故障率评估结果分别为0.0248次/a、0.0317次/a、0.0447次/a。由此可以看出,在风电变流器的可靠性评估中,若只考虑平均功率大小对其的影响,显然会导致忽略功率波动强度不同所带来的评估结果差异的问题。因此,在风电变流器的可靠性评估中有必要同时考虑变流器输出功率大小和功率波动强度的影响。
4.2 功率波动强度对变流器可靠性评估的影响
由第4.1节的分析可知,在相同平均功率大小下,功率波动强度不同会对变流器IGBT结温均值和结温波动的分布产生影响,因此,为了进一步分析不同功率波动强度对变流器可靠性评估的影响程度,本节采用第4.1节的数据处理方法,对平均功率保持1.0 MW不变,在不同功率波动强度下变流器的故障率进行计算,其评估结果如图8所示。
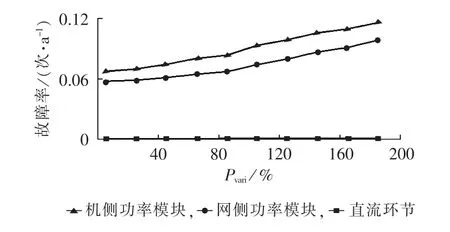
图8 平均功率保持1.0 MW不变时,不同功率波动强度下风电变流器故障率评估结果Fig.8 Results of converter failure rate evaluation for different power fluctuations with same average power of 1.0 MW
由图8可以看出,随着功率波动强度的增加,变流器各模块的故障率也将增加。此外,评估的机侧功率模块的故障率始终高于网侧功率模块的故障率,且随着功率波动强度的增加,机侧功率模块和网侧功率模块的故障率评估结果差异增大,进一步说明与网侧功率模块相比,机侧功率模块的可靠性受功率波动强度的影响更大,这与实际风电机组运行时,由于直流环节的稳压作用,机侧功率模块比网侧更容易受功率波动强度的影响是吻合的。
5 结论
基于多状态概率分析法,以功率大小和功率波动强度对变流器的运行工况进行二维状态划分,利用热应力因子和温度循环因子衡量可靠性变化,形成元器件故障率统一计算模型。利用变流器元器件结温计算方法,结合雨流法提取结温载荷循环信息,提出风电变流器系统级可靠性评估模型,并以某风电场SCADA信息为例,对可靠性评估模型的收敛性和不同方法的评估结果进行比较,并分析功率大小和功率波动强度变化对机侧和网侧变流器故障率的影响。所得的主要结论如下。
a.通过实际风电场运行数据的变流器可靠性评估表明,本文所建评估模型具有收敛性,计算的故障率结果和现有可靠性数据基本一致。本文建立的评估模型同时考虑功率大小和功率波动强度的影响,所得的故障率评估结果比仅考虑功率大小方法的评估结果大。相比而言,仅考虑功率大小评估方法的故障率计算结果较乐观。
b.功率大小和功率波动强度的变化都会影响变流器IGBT结温均值和结温波动的分布,在变流器可靠性评估时有必要同时考虑功率大小和功率波动强度2种因素。当保持功率大小不变时,风电变流器故障率会随着功率波动强度的增加而增大。
c.评估的风电变流器机侧功率模块的故障率高于网侧功率模块、直流环节的故障率,且随着功率波动强度的增加,变流器故障率也在增加,特别是机侧功率模块的可靠性受功率波动强度的影响更大。
本文中的算例所采用的风电机组SCADA数据记录时间尺度为1 min,因此,算例考虑了所有大于1 min时间尺度的结温循环对器件疲劳累积所造成的影响,然而没有考虑高频结温循环对变流器可靠性的影响。事实上,考虑到功率器件内部以及功率器件与散热器的热容对热传导的影响,其导热回路存在明显的迟滞作用,时间尺度越小,迟滞作用越明显。因此,简单地靠提高SCADA记录数据的频率不能准确反映功率器件结温的高频变化。这就需要根据功率器件的详细热网络模型以及风机的实际控制状态建立更加详细的可靠性评估模型,这也将是下一步研究的重点。
