基于SFBC MIMO-OFDM系统的峰均比抑制算法

张 博，李 辉，程 伟

（西北工业大学 电子信息学院，陕西 西安 710129）

0 引 言

作为4G无线宽带移动通信的关键技术，多输入/多输出的正交频分复用（MIMO-OFDM）是多天线技术和正交频分复用技术的结合方案，具有抗多径能力强、频谱利用率高、数据速率快等优点，但同时继承了OFDM技术峰值平均功率比（Peak-To-Average Power Ratio，PAPR）高的缺点。目前，大量文献集中在对STBC MIMO-OFDM和SFBC MIMO-OFDM系统的高PAPR降低技术进行了研究。与STBC MIMO-OFDM系统进行比较，SFBC MIMO-OFDM系统具有更优的抗多径时变衰弱信道能力，并已被TD-LTE制式采用。针对SFBC MIMO-OFDM系统高PAPR的问题，文献[1-2]均通过对输入序列进行两次分割，然后分别对各子序列进行相位旋转或交换产生多个候选序列，从中选择传输峰均功率比最小的候选序列。文献[3-4]充分研究了SFBC编码序列后的不同天线时域特性和相关性，并以PAPR性能为代价提出仅使用一次IFFT计算实现低复杂度抑制PAPR算法。文献[5-6]提出了一种接收端盲检测算法，实现无SI传输的抑制PAPR算法。上述所有文献均在时域或者频域对序列进行线性处理产生候选序列，并未考虑多天线的空间自由度，因此PAPR降低幅度有限。文献[7-9]虽然考虑了空间自由度，但是复杂度与天线数量和子块数成正比，不利于算法的实际工程应用。通过上述分析，本文提出了一种基于SFBC MIMO-OFDM系统的低复杂度抑制PAPR的空频变换算法。

1 系统模型和PAPR定义

为简化计算，系统模型为发射天线数Tx=2，接收天线数Rx=1的Alamouti SFBC-OFDM[10]系统。该模型可以推广至多天线系统。

在Alamouti SFBC-OFDM系统的发射端，MIMOOFDM系统的子载波数为N，对频域数据符号序列X0=[X1,X2,…,XN]T进行 Alamouti空频编码，再经过OFDM调制后从不同天线上发射；在系统接收端通过OFDM解调和空频译码恢复频域符号。Alamouti空频编码对X0内的每两个相邻数据符号Xk和Xk+1进行编码产生分组向量：

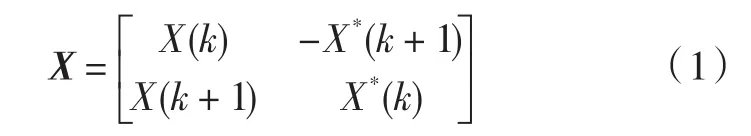
其中在第k个符号周期内，X(k),X(k+1)将分别从第一、二根天线 Tx1发射；在第k+1个符号周期内，-X*(k+1),X*(k)将分别从第一、二根天线Tx1发射。其中“*”表示共轭。

对于一个具有N个子载波数的MIMO-OFDM系统，第m根天线上的第n个子载波上的传输频域序列为Xm,n。则MIMO-OFDM系统第m根天线上的复基带发射信号表示为：

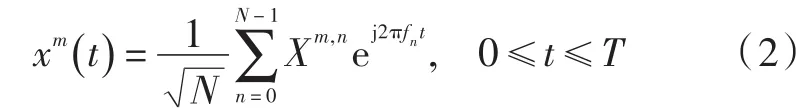
式中：fn=n×f0为第m根天线上第n个子载波上的载波频率，f0=1 T，T为OFDM符号周期。对Alamouti SFBC-OFDM系统的第m根天线的PAPR定义为：

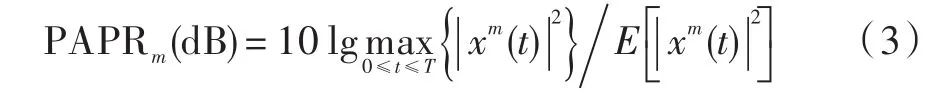
式中E[]·表示均值。在比较PAPR降低性能时，通常使用互补累积分布函数（Complementary Cumulative Distribution Function，CCDF）来表示一个OFDM符号的PAPR超过门限PAPR0的概率。PAPR的互补累积分布函数定义为：

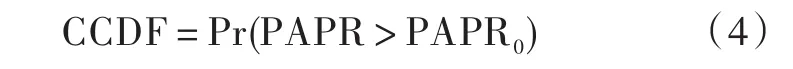
2 IFFT相关性质

2.1 IFFT线性叠加性质

令 X1和 X2均为N点序列，且分别是 x1，x2的频域符号，并令 X=aX1+bX2，则 x=ax1+bx2。

2.2 IFFT的循环移位特性

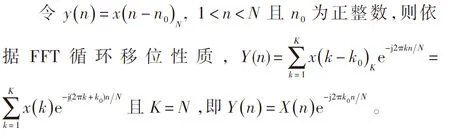
3 天线间空频变换算法

经过SFBC编码后，将产生向量空频码字X1=[X(0),-X*(1) ,…,X(N-2),-X*(N-1)]T和 X2=[X(1),X*(0),…,X(N-1)]，X*(N-2)]T，其 中 []*表 示 共轭 ；X1将 从 第 一 根 天 线 Tx1发射，X2从第二根天线Tx2发射。

3.1 空间交叉反向变换

图1中将 Xi,i∈(1,2)分成互不相交、长度相同的M个子块序列，且子块序列数为偶数。利用文献[11]的逐次旋转取反算法，将X11,X21旋转取反得4组选序列：

（1）原始序列：

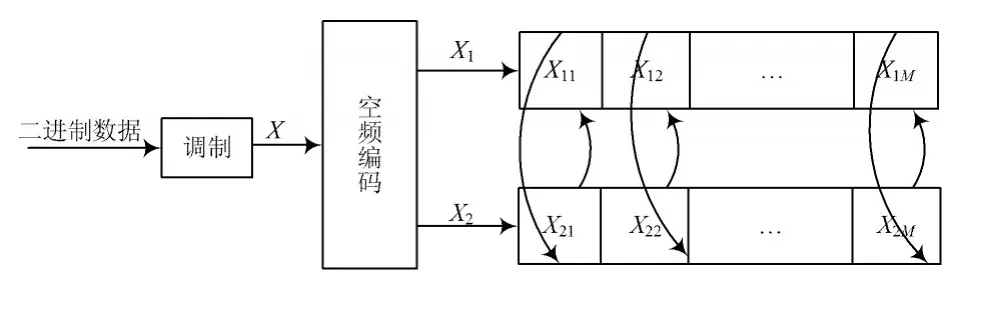
图1 基于SFBC MIMO-OFDM的旋转反向算法框图

采用MINMAX准则，选择四组候选序列中使OFDM符号X1，X2的PAPR最大值最小的一组序列。同理，在前一组被选序列的基础上，对另外M-1个子块逐次进行上述操作，最终产生4×M组候选序列，选取具有PAPR最大值最小的一组候选序列。容易推导，对子块进行旋转取反操作不影响符号间的空频正交特性。

3.2 频域内子块循环移位

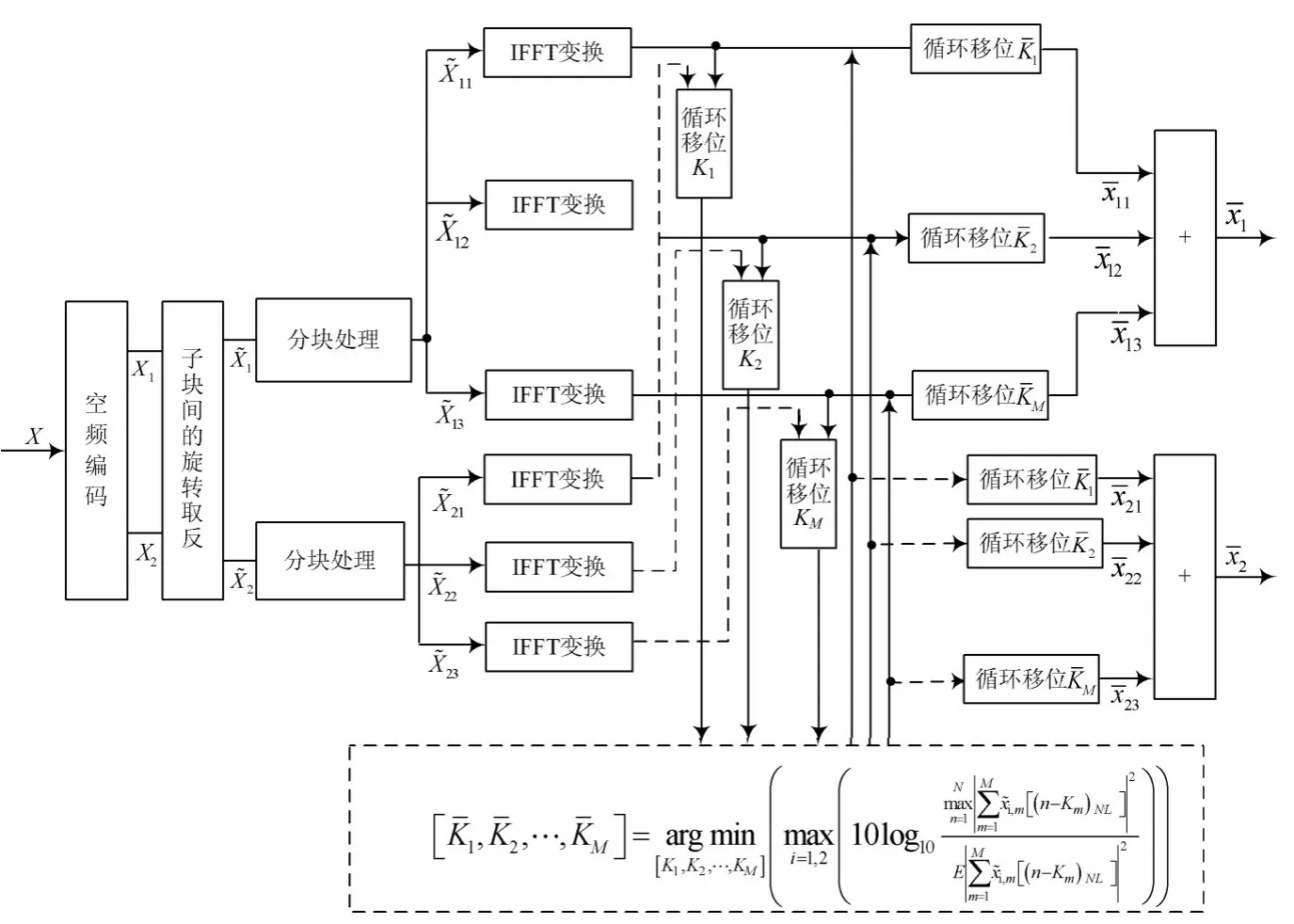
图2 SFT算法原理框图

子块循环序列移位工作原理如下所示：

（2）对步骤1选择的一组候选序列中的第2个子块进行以K位为步长的循环移位，至少产生个候选序列数，采用MINMAX准则选取具有PAPR最大值最小的一组序列。同理，对剩下的个子块序列的时域信号逐次进行上述循环移位操作。整个过程中最终产生至少×M组候选序列数，采用MINMAX准则选取具有PAPR 最大值最小的一组候选序列。最后对和上变频，分别从天线1和天线2发射。

3.3 计算量分析

算法计算量主要集中在IFFT变换的复数加法和复数乘法。如图2所示，将频域序列分块后，对每一个频域子块序列扩展成L×N个点并进行IFFT变换，因此对和进行处理需要2M个IFFT变换。参考文献[2]的计算量降低算法，对扩展子块序列,i∈(1,2)且m∈(1,2,…,M)进行V=2的交织分割生成且服从：

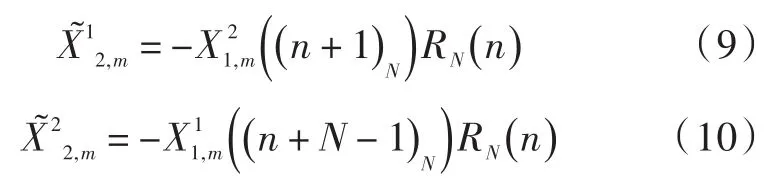
天线1共有M个子块，每个子块有2个交织分割的最小子块，需要进行两次IFFT运算。天线1需要的复数乘法总数为，天线2的交织子块所需复数乘法总数+4NM。参考文献[3]，分别是的时域信号，满足：

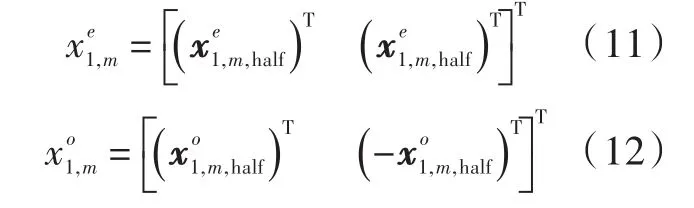
4 仿真结果及性能分析

本文使用Matlab软件作为仿真工具。采用Alamouti SFBC MIMO-OFDM系统，使用105个统计独立的OFDM信号进行仿真，调制使用16QAM，每个OFDM符号占用256个子载波，过采样数取L=4。

如图3所示，当信号的CCDF为103时，取子块数M=8，16或32，SFT算法的PAPR性能比SFBC-ST算法或协同部分传输序列算法（C-PTS）[12]优于约0.8 dB和1.0 dB。考虑SFBC-ST和C-PTS的比较，结果表明利用天线间的空间变换算法优于C-PTS；考虑SFT和SFBC-ST的比较，结果表明子块间循环移位过程在空间变换的基础上能够提高约0.8 dB的PAPR性能。

如图4所示，当信号的CCDF为103时，子块数M=32，单位循环移位数circs=16时算法SFT的PAPR性能最好。当子块数M相同时，循环移位数circs取16，32或64时的PAPR性能变化不大，表明M值取定后，循环移位数对PAPR性能影响有限。而当单位循环移位数circs相同，子块数M取8，16或32时的PAPR性能相差近0.3 dB，表明circs取定后，子块数对PAPR性能有一定的影响。

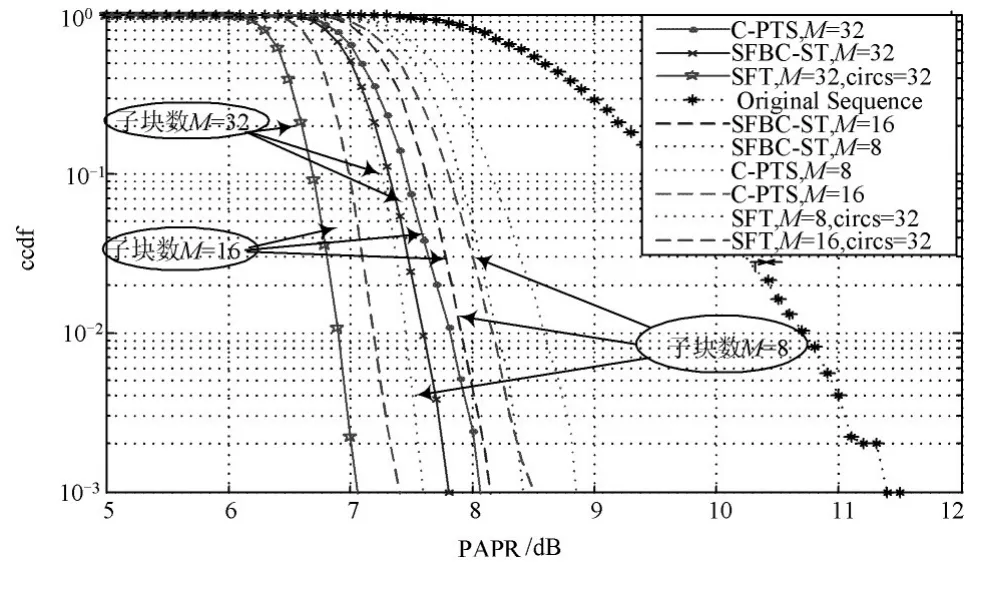
图3 SFT，SFBC-ST与C-PTS的PAPR比较较

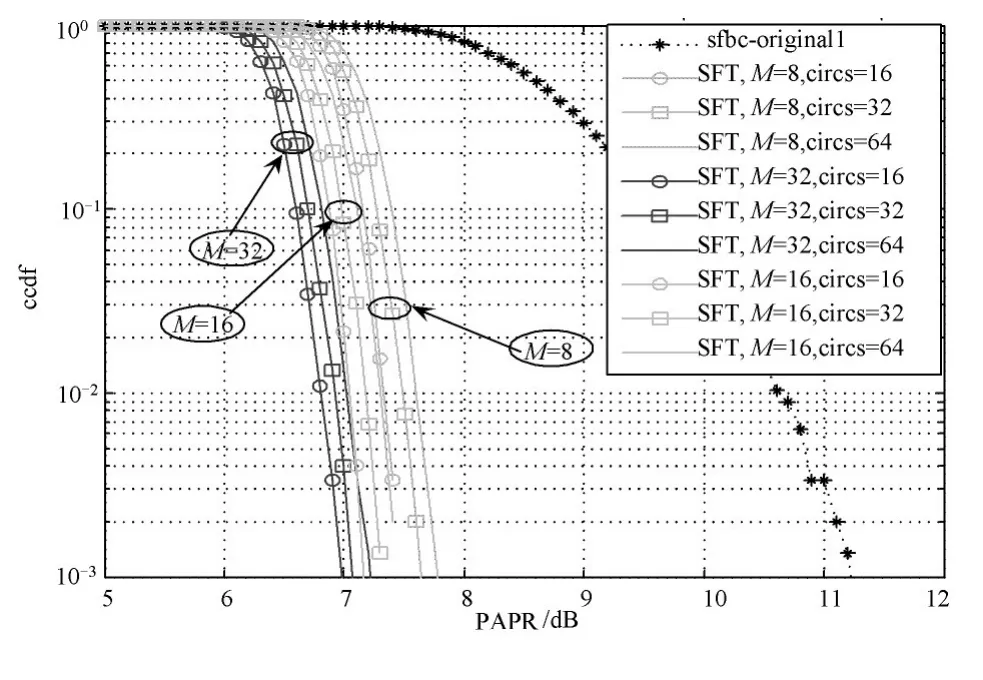
图4 取不同M，circs值时的SFT算法PAPR性能比较

5 结 语

本文从空间自由度的角度出发，提出了一种有效的的空频变换算法，即对OFDM信号子块进行天线间的空间交叉变换和循环移位过程产生候选序列数；与传统算法相比，SFT实现近1 dB的PAPR性能提高。通过计算量分析表明，结合IFFT特性和SFBC正交特性实现了算法的低复杂度特性。该算法能够扩展至多天线系统，是一种适合于多天线系统的降低PAPR高效的信号处理算法。

[1]沙溢，陈俊鑫，王光兴.基于SFBC结构的MIMO-OFDM系统峰均比抑制方法[J].通信学报，2009，30（10）：114-117.

[2]沙溢，陈俊鑫，陈进，等.一种降低SFBC MIMO-OFDM系统峰均功率比的新算法[J].东北大学学报：自然科学版，2010（4）：503-506.

[3]LI Chih-peng，WANG Sen-hung，CHAN Kuei-cheng.Low complexity transmitter architectures for SFBC MIMO-OFDM systems[J].IEEE Transactions on Communications，2012，60（6）：1712-1718.

[4]WANG Sen-huang，LI Chih-peng.A low-complexity PAPR reduction scheme for SFBC MIMO-OFDM systems[J].IEEE Signal Processing Letters，2009，16：941-944.

[5]NAEINY M F，MARVASTI F.Selected mapping algorithm for PAPR reduction of space-frequency coded OFDM systems without side information[J].IEEE Transactions on Vehicular Technology，2011，60：1211-1216.

[6]HU Wei-wen，CIOU Ying-chi，LI Chih-peng，et al.PAPR reduction scheme in SFBC MIMO-OFDM systems without side information[C]//IEEE International Conference on Communications.[S.l.]：[s.n.]，2013：4708-4712.

[7]JIANG Tao，LI Cai.Simple alternative multisequences for PAPR reduction without side information in SFBC MIMO-OFDM systems[J].IEEE Transactions on Vehicular Technology，2012，61：3311-3315.

[8]GONG Peng-chen，SHAO Zhen-hai.PAPR reduction scheme in SFBC MIMO-OFDM based on transformation[C]//2010 International Conference on Computational Problem-Solving（ICCP）.[S.l.]：[s.n.]，2010：108-110.

[9]YANG Ou-yang.Peak-to-average power ratio reduction by crossantenna translation for SFBC MIMO-OFDM systems[C]//Vehicular Technology Conference.[S.l.]：[s.n.]，2009：1-4.

[10]Alamouti S.A simple transmit diversity technique for wireless communications[J].IEEE J Sel Areas Commun，1998，16（8）：1451-1458.

[11]TAN Mi-zhou，LATINOVIC Z，BAR-NESS Y.STBC MIMOOFDM peak-to-average power ratio reduction by cross-antenna rotation and inversion [J].IEEE Communication Letters，2005，9：592-594.

[12]WANG L，LIU J.Cooperative PTS for PAPR reduction in MIMO-OFDM[J].Electronics Letters，2011，47（5）：351-352.