基于相互迭代混沌算法实现数据加密及算法对比

蔡苏亚

（陕西工业职业技术学院 信息工程学院，陕西 咸阳 712000）

一直以来混沌理论在非线性学科中占据中较为重要地位。混沌信号具有非周期性连续宽频带，与噪声类似的特点，并且在一定的时间内是不可预估的，因此非常合适在应用保密通信方面领域[1-3]。混沌系统是把很多有序的操作整合在一起，然而任意一个有序子量处于正常状态下都无法起到决定性地位，因此混沌看似是任意随机的，实际都是明确的量。最先观察到混沌现象的是Lorenz，经过一段时间以后，学者研究分析得出一系列混沌系统，如映射ehua电路、chen′s电路、Rossler系统等[4-7]。混沌和密码学有很多几乎一样的特点，因此，涉及在密码的领域中，混沌也被大量应用[8-9]。基于信息论，香农验证了一次一密可靠，实质是满足了加密的密钥流大于信息数据所占据的长度。然而在现实中是无法实现的，怎么利用短密钥序列形成长密钥流序列，这个问题在密码学是亟需解决的[10-13]。近几年应用当中发现混沌理论在数据加密方面应用优势并不明显，特别表现为抗密钥穷举攻击、加密速度等方面[14-16]。文中基于这一背景，进行了复合混沌算法实现数据加密的性能改进及对比分析，结果很好地改进了混沌算法存在的问题。这一研究对混沌密码学的进一步改进应用具有明显的理论和实践意义。

1 相互迭代的优化设计

1.1 Logistic映射混沌序列优化

Logistic模型一开始是表达昆虫种群增长量的模型，也叫做虫口模型。下面设计针对Logistic混沌序列进行优化，Logistic模型的动力学过程如下：

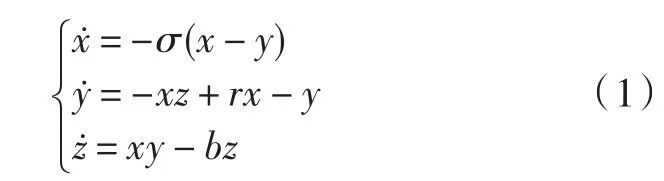
式中的参数较为经典的取值是σ=10，r=28，b=8 3。当σ，b仍取值为10和8 3 ，此时如果r＞24.75，那么系统处于混沌状态。由于系统输出的实值混沌序列存在如下缺点：x，y，z的值域各不相同，不利于批处理；x，y，z局部取值呈现单调性，易受线性预测攻击；x，y，z自相关特性非理想的δ函数，互相关特性非理想的零特性，难以保证不可预测性，而且系统多输出特性也得不到充分利用。为了尽可能地避免这些缺陷，提出了一种改进方法对混沌序列做优化，设计了一个模型，方程如下所示：

式中：x′，y′，z′是经过优化后的序列；m是控制参数，能够起到提升序列取值的不规则性；round（）是最接近整数函数，能够实现混沌优化序列。

1.2 优化算法过程

通过式（2）可以得到经过优化处理的3个混沌序列x′，y′，z′，形成3个置乱矩阵，利用其分别对RGB彩色图像的3个分量做置乱加密处理。通过优化后的混沌序列可以形成对应的置乱矩阵PM×N。该置乱矩阵中的任意一个元素Pij都在[1，2，…，M×N]的范围里，如果有Pij=Pkl，且只有满足i=k，j=1时才成立。如果M=4，N=4时，那么P就是4×4的矩阵，通过优化混沌序列从而形成16个实数值的混沌序列，把这些序列按照从大到小进行排序，用1～16做标识，那么就能够得到序列：4，6，7，3，1，2，8，15，10，12，14，13，16，11，9，5。以行排列为4×4的置乱矩阵 P4×4为：

通过使用非线性置乱的方法，把图像IM×N中子元素和对应的PM×N中的元素做置乱处理，这里设计的详细过程如下：

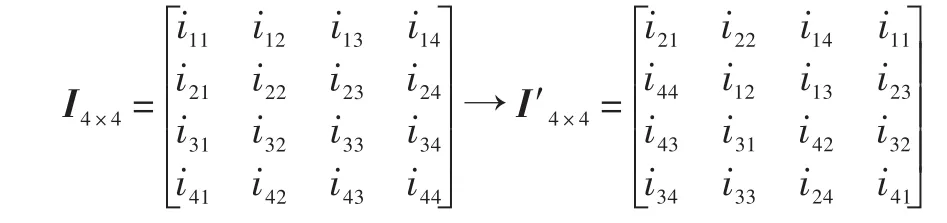
算法程序的过程如下：

先定义一个寄存器变量ch。

register char ch；

再进行加密处理。

while（str1[++j0]）；

ch=fgetc（fp1）；

while（!feo（ffp1）/*加密算法开始*/

{

fputc（ch^str1[j＞=j0?j=0；j++]，fp2）； /*异或后写入fp2文件*/

ch=fgetc（fp1）；

v++； /*统计视频字节数*/

}

2 数据加密的安全性的分析

一个较好的加密算法，不仅要其安全可靠性能高，而且要其运行的速率快。在前面的叙述中，已经知晓混沌方程进行迭代是能够生成伪随机数列的。密钥循环一次大概能够加密100 kb视频数据信息。又因为由于周期很长，并且还是伪随机数列，所以在安全方面的性能得到了较好的保障。另外，鉴别时效性主要是取决于验证程序能不能较为快速的加密。在进行验证时，选取了约1 GB大小的各种不同类型的视频文件。凭借较大信息量的视频文件能够很明确地显示出程序加密地速度的快慢。先对一个710 MB扩展名为“dvd.mp4”以及一个970 MB扩展名为“soldier.rmvb”视频文件进行测试，其测试所得数据结果见图1。

图1 测试所得数据

在做验证加密时会生成一些文件。其中，文件hundun1.mp4与hundun2.rmvb都无法打开，然而文件de⁃code1.mp4与decode2.rmvb能够打开。经验证可以知道解密之后的视频和最初的视频是一样的。另外，还可知加密以及解密所需要的时间不超过1 min。该时间是把生成密钥流以及加密视频的所需时间计算在内的，其速率是超过10 MB/s。由此可知，利用混沌加密的算法的适用性强。该方法不仅能够确保安全，同时具有较快的加密速率。假如破解视频所耗的成本比视频自身所拥有的价值还要大，于是进行破解就显得多余。虽然对于安全要求非常高的场合是不适用的，然而在人们日常生活若需加密的视频文件时，使用该方法是较好的方法。加密系统的关键性能是自身抵抗外界攻击的能力，若抵抗能力越强，说明该系统安全系数越高。破解人员对加密系统的攻击实质就是此系统密钥流进行的攻击，因此混沌Logistic映射的抵抗攻击的性能实际上就是等同于整个加密系统抵抗攻击能力。如果N＞μ，μ＝3.569 945 6时，Logistic映射处于混沌状态，当周期N无限接近于∞时，如果攻击人员采用穷举法的方式做蛮力攻击，那么要进行2N次，所以考虑到实际情况以及成本的因素，都不可能顺利完成的。在实际应用里，不可能满足精度无穷大的要求，如果在没有采用参数μ动态累加产生器的情况下，序列周期是N′，此时有攻击人员采取穷举法做蛮力攻击，那么就得做N′次运行。然而，在采用参数μ动态累加产生器的情况下，序列周期是22′rN，此时有攻击人员采取穷举法做蛮力攻击，那么得做2′2rN次运行。加密算法，关键的优势功能是在整体的加密结构进行了优化处理、科学的安排及长度为128的密钥。如果进行强力攻击效果最突出，则以位方式得到密钥得进行2128次加密运算，就会耗费1012年的时间。面对IDEA采取强力的方式进行攻击，那么生成解密子密钥的速度远远不及加密子密钥速度。可以看出，解密需要耗费的时间会很多。综上所述，采用混沌利用混沌算法生成高性能的密钥，并且利用IDEA优质性能以及高质量的加密体系，确保了整个加密系统具备了很高的安全性能。

3 图像应用数据的加密实验

3.1 实验设计

本文图像采用图2（a）所示，把分量图合成为彩色图像后的加密图像见图2（b）。这里迭代过程应用了1 000次。

图2 实验对象和加密图像

3.2 保密性测试优势

为了验证算法的保密性性优势，图3进行如下实验：（a）为参数r的偏差为10-10次方时的错误解密图像；（b）为初值xo的偏差为10-10次方时的错误解密图像。从算法改进结果来看图像已经发生了视觉方面的色彩改变，显然图像必将梗难破译，有理论分析可知对图像加密的需要进行3MN次操作，显然这一结果验证了算法保密性方面的优势。

3.3 抗攻击测试

为了分析图像的抗抗击性，图4分别进行如下实验：（a）加密后的图片经过压缩改进的解密图像；（b）则采用高斯噪声后的解密图像，从图片视觉表现来看，算法显然实现了解密图像效果保持，这验证了算法有较强抗攻击能力。

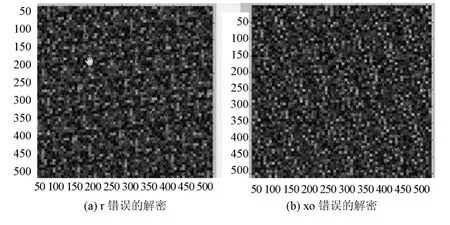
图3 r和x o错误的解密

图4 JPEG压缩和高斯噪声解密

4 算法对比

空域复合加密算法与比特移位加密算法的比较如表1所示。

表1 空域复合加密算法与比特移位加密算法的比较

由表1可知，与改进的混沌加密算法对照，本文算法有主要的三个优点：第一，在有限精度下密钥空间从1016≈253扩大到1048≈2158，很大程度上提高了抗密钥穷举攻击的能力；第二，一次能加密多个比特，并且比特移位操作速度远远大于比特异或操作，所以该算法加密速度比空域复合算法的速度快。第三，因为xi的随机性，在加密的流程中破坏了原图像像素的独立性，使得破译的难度加大。

5 结 语

设计过程中，采用复合混沌方程是形成密钥流的方式，由于混沌方程能够因为反复迭代生成类似的随机数列，把其数列当成是加密程序的密钥与加密算法的要求是相当吻合。若密钥完全是随机的，则想破译密很难实现。因此，密钥随机性越强，加密算法就越安全。设计加密时，直接使用异或方式加密，该方法的加密速率是很高的。另外，还要定义一个寄存器变量，采用此变量存取加密时形成的字符，同时也提升了加密的速度。最后，测试程序执行所需花费的时间，也验证了此程序能够快速加密的功能。

[1]吴昊.基于DES算法和RSA算法的数据加密方案[J].焦作工学院学报：自然科学版，2002（5）：395⁃396.

[2]张翰林，王青山，邹永初.复合混沌系统的矢量数据加密研究[J].测绘科学，2012（5）：87⁃89.

[3]高为民，朱凌志.混沌加密算法在J2ME平台中的应用研究[J].计算机仿真，2013（4）184⁃187.

[4]张帆.基于Lorenz⁃Duffing复合混沌系统的彩色图像加密[J].微电子学与计算机，2013（10）：62⁃65.

[5]赵雪章，席运江.一种基于混沌理论的数据加密算法设计[J].计算机仿真，2011（2）：120⁃123.

[6]王妍芬，杨风暴，李伟伟.一种基于四维混沌神经网络的通信数据加密算法[J].电子测试，2011（4）：19⁃22.

[7]陈作新.基于混沌和AES算法的数字图书馆数据加密方案[J].农业图书情报学刊，2012（4）：52⁃55.

[8]孙克辉，张泰山.基于混沌序列的数据加密算法设计与实现[J].小型微型计算机系统，2004（7）：1368⁃1371.

[9]杨欣，李强，黄席樾.基于混沌算法的软硬件相结合的加密方法[J].重庆大学学报：自然科学版，2005（2）：74⁃76.

[10]包浩明，朱义胜.基于混沌参数调制的数据加密算法[J].电路与系统学报，2009（4）：34⁃38.

[11]高铁杠，陈增强，袁著祉，等.基于混沌密码流的IC卡数据加密算法设计与实现[J].仪器仪表学报，2006（1）：58⁃60.

[12]WU Chuan⁃Kun.Set signatures and their applications[J].Science in China（Series F：Information Sciences），2009（8）：1346⁃1357.

[13]HAN Yan⁃yan，HU Yu⁃pu.A digital signature⁃based visual cryptography scheme for image discrimination and manage⁃ment[J].Journal of Electronics，2009（5）：631⁃636.

[14]YOU Lin，SANG Yong⁃xuan.Effective generalized equations of secure hyperelliptic curve digital signature algorithms[J].Journal of China Universities of Posts and Telecommunica⁃tions，2010（2）：100⁃108.

[15]罗启彬.基于混沌序列的遥测PCM数据加密算法[J].无线电工程，2007（11）：37⁃39.

[16]席丽筠.基于混沌理论的数据加密算法[J].合作经济与科技，2008（18）：94⁃95.