基于自适应遗传算法的连续时空最优搜索路径规划研究
2015-09-18张献任耀峰王润芃海军工程大学理学院湖北武汉430033
张献,任耀峰,王润芃(海军工程大学理学院,湖北武汉430033)
基于自适应遗传算法的连续时空最优搜索路径规划研究
张献,任耀峰,王润芃
(海军工程大学理学院,湖北武汉430033)
针对连续时空最优搜索者路径问题,利用随机微分方程描述Markov运动目标,建立了同时优化搜索者方向和速度的规划模型,并考虑了搜索速度对探测能力的影响。设计了一种新颖的自适应变异遗传算法,算法采用较高的变异概率作用于父代精英个体组,通过引入3种控制因子对变异方向和幅度进行自适应控制,动态调节局部搜索和全局搜索的平衡。在对方向未知的逃离目标搜索算例中,得到了近似对数螺旋曲线的搜索路径;在直升机搜索多目标的路径规划中,提供了合理有效的搜索方案。算法对比表明所给出的算法在全局优化能力和稳定性上有明显的优势,适用于求解连续搜索路径规划问题。
运筹学;最优搜索;连续时空;Markovian目标;自适应变异遗传算法;反潜搜索
0 引言
最优搜索者路径问题(OSPP)是搜索论中搜索者运动受到约束的一类复杂优化问题,要求搜索者在有限资源约束下,构造一个搜索路径使得搜索效益最大,目前在海上救援、无人机侦查、反潜搜索[1-3]等诸多领域有广泛的应用。
根据是否对时间和空间进行了离散化处理,OSPP可大致分为离散时空OSPP和连续时空OSPP两类[4]。1986年Trummel和Weisinger已经证明了在离散时间和空间下,对于静止目标OSPP的复杂度至少是NP-hard[5].目前无论对于哪类问题,许多学者都将算法的设计与优化作为问题研究的一个重要方向。在离散时空OSPP方面,已有较多的方法被采用,例如动态规划技术[6]、分支定界法[7-9]、割平面法[10]、启发式算法[3,11-12]。但由于离散化处理的需要,使得模型在目标和搜索者运动过程的表达上与实际情况相差较大。
为了使模型更贴近实际,部分文献对更为复杂的连续时空OSPP展开了讨论。Ohsumi[13]和朱清新等[14]利用最优控制理论研究了此类问题,但是目标和搜索者的运动需要满足严格的微分方程,这一要求局限了模型的应用范围。在宽泛的问题描述下,Kierstead等[15]首次将遗传算法(GA)应用于连续时空OSPP,针对一些探测环境复杂的搜索问题,提出了一种基于路径几何关系进行遗传操作的GA,得到了令人满意的搜索方案。Cho等[16-17]设计了一种基于搜索者方向编码的高变异率GA,讨论了静止目标和简单定向运动目标的搜索问题,相比Kierstead的算法优化效果有所提高,体现出GA在求解此类搜索问题方面的优势。然而这两种模型的不足之处是均假定目标为静止或作简单的匀速运动,搜索者的速度也为固定的,不利于实际应用。并且所给算法的优化效果受初始种群的影响较大。
本文研究更为一般的连续时空Markov运动目标的搜索问题。首先利用随机微分方程表达目标运动模型,同时考虑搜索速度对探测能力的影响,建立了搜索者模型,对搜索者方向和速度同时进行优化。然后针对OSPP的特点,设计了一种自适应变异遗传算法(AMGA).该算法采用较高的变异概率作用于父代精英个体组,丰富了种群的多样性;通过引入3种控制因子,对变异方向和幅度进行自适应控制,动态调节局部搜索和全局搜索的平衡,增强了算法的寻优能力和稳定性。最后通过仿真分析、实例应用及算法对比验证了AMGA的有效性。
1 目标模型
文献[15-17]在连续时空下讨论了静止目标和简单定向运动目标的OSPP.为使模型更一般化,考虑一个R2空间中的连续时间Markov运动目标{X(t),t≥0}.利用随机微分方程理论[18]对目标的运动过程进行描述:
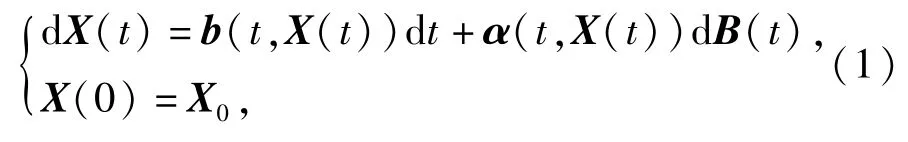
式中:X(t)∈R2;b(t,x):[0,+∞)×R2→R2,b(t,x)为漂移系数;α(t,x):[0,+∞)×R2→R2×2,α(t,x)为扩散系数;B(t)是二维布朗运动;X0为初始位置。对(1)式的详细表达为
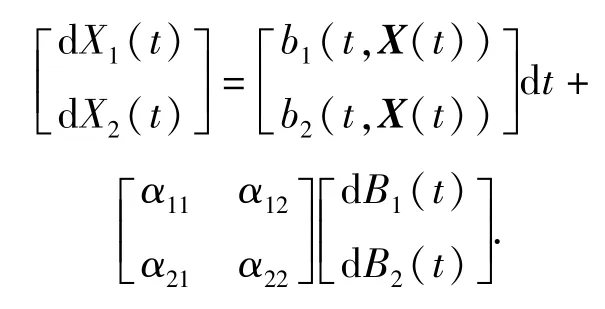
在搜索问题中,X(t)表示目标的运动位置,b(t,X(t))表示目标的速度矢量,B(t)代表环境等因素的干扰,α(t,X(t))则表示干扰的幅度大小。这种随机微分方程描述方法同时考虑了目标的运动参数以及环境等因素的影响,能够较好地描述目标的运动状态。
本文假定目标的运动不受搜索者策略的影响,即目标不会对搜索者的行为做出反应,所讨论的问题属于单向搜索范畴。
2 搜索者模型
2.1搜索者运动模型
在实际中,搜索双方通常在一定时间段内保持稳定的运动方向和速度,每隔一段时间根据情况进行调整(如舰船和潜艇)。现将方向、速度稳定不变的运动过程视为一个阶段(Step).搜索路径的表达包括以下几个要素:搜索者起始坐标SS、搜索时间Ts、阶段时长Stepts、方向θs和速度vs(下标s表示搜索者),其中θs∈[0,2π),vs∈[vmin,vmax].需要指出的是,本文模型忽略各阶段在方向调整上所消耗的时间以及由此引起的路径偏差。
在搜索路径的优化过程中,文献[15-17]都将vs固定考虑,只将θs视为变量。为了更准确地描述实际问题,本文在阶段时长Stepts视为常数的前提下,将方向θs和速度vs同时作为问题的决策变量进行优化(见图1)。
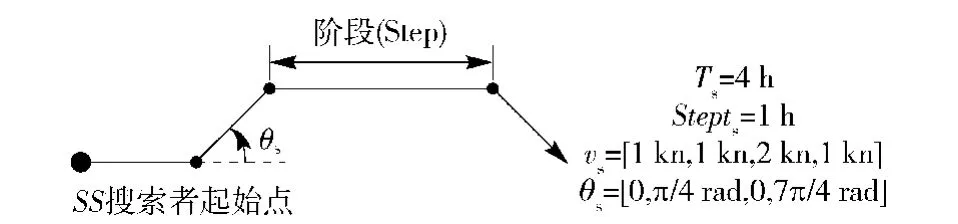
图1 搜索路径的表达Fig.1 Search path
图1展示了一条简单的搜索路径:搜索者的搜索时间Ts=4 h,各阶段时长Stepts=1 h,各阶段的速度及方向如图所示。由于考虑了搜索速度的变化,这里所讨论的“搜索路径”不只表示搜索者的运动轨迹,而且还包涵了路径上的速度信息,实际上是一种搜索方案。为了便于叙述,本文仍使用“搜索路径”一词。
2.2探测模型
探测过程中,搜索者一般利用传感器采集目标信息。声纳是舰艇搜索水下目标常用的设备之一,其探测概率是一个受物理环境、信号功率等多种因素影响的复杂函数。本文选用理想的探测模型,即当目标与搜索者的距离小于等于声纳作用距离L时,探测到目标的概率为1,否则为0.
实际问题中,搜索者速度往往会对探测能力产生影响,例如L会受到舰船自身噪声的影响:通常当舰船速度低于某临界值时,自身噪声保持不变;当速度高于临界值时,自身噪音会随速度的加快而增强[19]。因此L与搜索速度有着一定关系,然而这种关系在实际中往往十分复杂。(2)式给出了一个简单函数,表征路径各阶段的声纳作用距离与搜索速度间的关系,如图2所示。

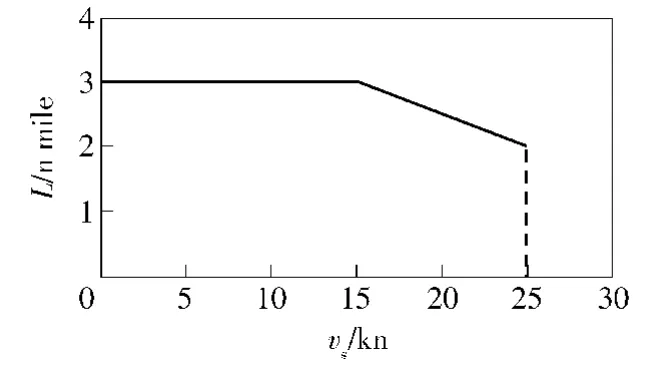
图2 声纳作用距离与搜索速度的关系曲线Fig.2 Relation between detection rang and search velocity
3 自适应变异遗传算法
本节针对连续时空OSPP,设计一种AMGA.
3.1问题描述
OSPP要求搜索者按照构造的物理路径实施搜索,通过合理配置资源使得搜索效益最大。本文利用累积探测概率(CDP)[19]评价路径的搜索效率,并作为搜索路径规划的目标函数和AMGA的适应度函数。在0≤t≤T时,对于任意一个可行的搜索方案ξ,t时刻的CDP记为FCDP(ξ,t),定义为时间段[0,t]内至少一次探测到目标的概率

对于一般的搜索路径,精确地求得FCDP的解析表达式是很困难的,可采用Monte Carlo方法近似计算[15-17]。
针对问题的特点,建立对搜索者方向和速度同时优化的搜索路径规划模型如下:
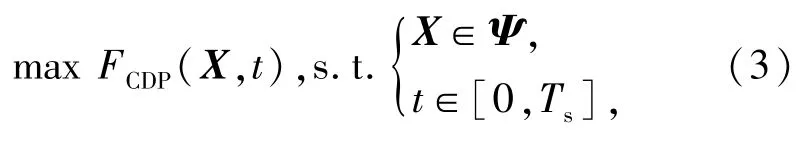
式中:决策变量X=(x1,x2,…,x2N)T表示一种搜索路径规划方案,N表示搜索路径阶段总数,(x1,x2,…,xN)T和(xN+1,xN+2,…,x2N)T分别表示搜索路径各阶段的方向θS和速度vs;FCDP(X,t)表示t时刻沿搜索路径X的累积探测概率,由于FCDP是t的单调递增函数,一般 t取 Ts;变量的约束条件 Ψ={X|xi∈[ai,bi]},ai<bi为实常数,i=1,2,…,2N,具体到问题中,Ψ={X|xi∈[0,2π],1≤i≤N;xi∈[vmin,vmax],N+1≤i≤2N}.
3.2个体编码方案
AMGA采用双链实数编码方案:每条染色体代表一条搜索路径,由两条并列的基因链组成,分别表示经过实数编码的搜索路径的方向和速度。将遗传种群记为,其中一条双链染色体表示为
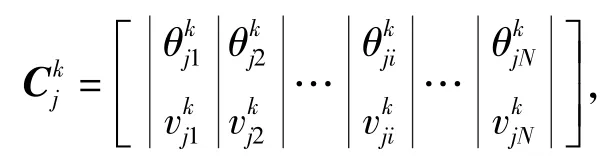
i=1,2,…,N;j=1,2,…,M;k=1,2,…,Gmax.
需要指出的是,在进化过程中双链染色体上同基因位的基因θi、vi一同进行遗传运算。
3.3遗传操作
在遗传操作方面,AMGA采用改进的交叉和变异算子引导种群进化。在详细讨论之前,需要强调一些重要参数的定义。
变异算子针对父代精英个体组实施变异操作,其中精英个体组为种群中适应度最高的一部分个体,将精英个体占种群的比例称为精英个体比率,记为PE.在每代进化过程中,两种遗传算子是独立运算的,得到的两组新个体组成子代种群。分别将这两组新个体占子代种群的比例称为交叉概率和变异概率,记为PC和PM(PC+PM=1).需要指出的是,这里对交叉概率和变异概率的定义与其他GA中的定义不完全相同。通过大量的实验和参数对比,本文选取PE=0.15,PC=0.25,PM=0.75.
3.3.1交叉操作
交叉操作采用轮盘赌法[20]从父代中选取一组个体,通过两两单点交叉得到新个体,起到丰富种群多样性的作用。其中交叉点在染色体长度的1/4~3/4处随机选择,选取交叉操作的个体数为PC×M.
3.3.2变异操作的改进思路
变异的方向和幅度直接影响算法的效率和收敛速度,但在一般GA的变异操作中,基因的变更常常只通过简单地产生随机数替换父代基因,显然这种变异方式过于盲目。下面针对OSPP特点,从3个角度分析改进变异操作的措施:
1)利用父代最优个体自适应控制变异方向。由于进化过程中父代最优个体具有最高的适应度值,在种群中往往最接近全局最优解。因此可以利用其信息控制变异方向,使被操作的个体向接近父代最优个体的方向变异,引导种群进化。类似的思想在量子进化算法的旋转门操作和粒子群算法的速度更新方程中都有所体现,但这些算法大都选取当前最优个体来引导种群演化,而本文选取的是父代最优个体,这样可增强算法的全局搜索能力。
2)在搜索路径的不同阶段自适应控制变异幅度。在图3中,将路径1分别对不同阶段的方向作幅度相同的变异操作得到路径2和路径3.从图3中可以看出,阶段越靠前,方向的变化对搜索路径的改变越剧烈,即影响程度越大。将路径3第一阶段的速度作幅度相同的变异操作得到路径4.从中可以看出速度对路径的影响较小。变量类别与其变异时所处的阶段对路径的影响差异较大是OSPP与其他数值优化问题的一个关键区别。因此变异幅度应根据变量的类别与其所处的阶段自适应调整。
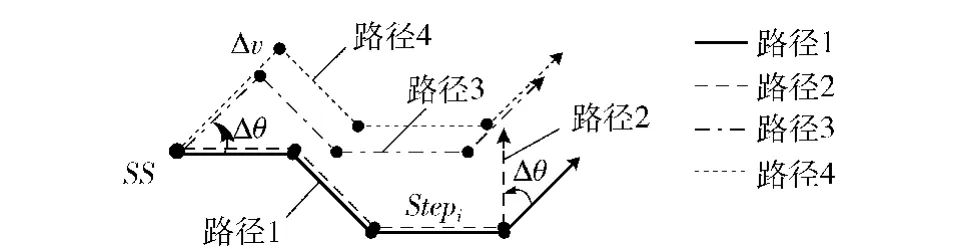
图3 不同搜索阶段方向和速度对搜索路径的影响Fig.3 Effects of direction and velocity on search path in different search steps
3)根据不同进化阶段自适应控制变异幅度。在进化前期变异有助于增加种群的多样性,而在进化后期,优秀个体逐渐接近最优解,应避免剧烈变异(例如方向的180o旋转)。因此变异幅度应随进化代数的增加自适应减小。
文献[16-17]给出了5种选取变异位置和变异基因个数的方法,并将其作用于父代最优解。AMGA则从父代精英个体组中随机选取PM×M个个体进行变异操作,进一步丰富种群的多样性。
3.3.3自适应变异策略
基于上述思路,本文对变异操作进行改进,提出下面的自适应变异策略:
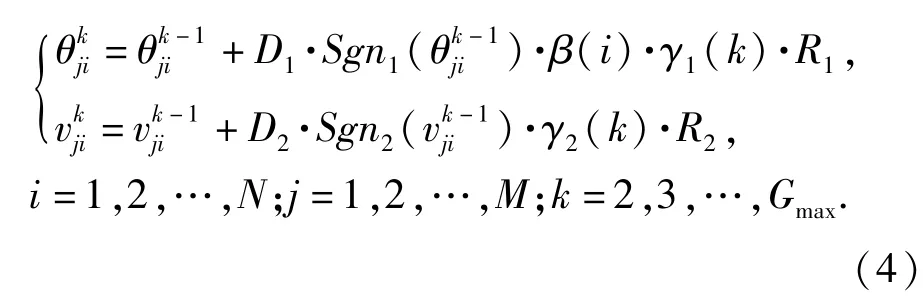

通过大量的实验和参数对比,本文选取的常数值和控制因子由(6)式~(8)式给出。在这些参数选择下,算法能够发挥出最佳的优化性能,得到稳定的运算结果。
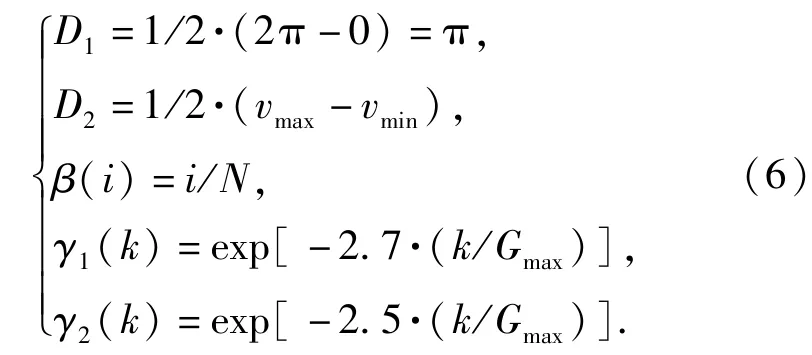
在变异方向控制因子Sgn(·)的设计上,利用父代最优个体的引导作用,将被操作个体向逼近父代最优个体的方向实施变异。首先将父代最优个体记为式中两类方向控制因子Sgn(·)分别由(7)式、(8)式确定:
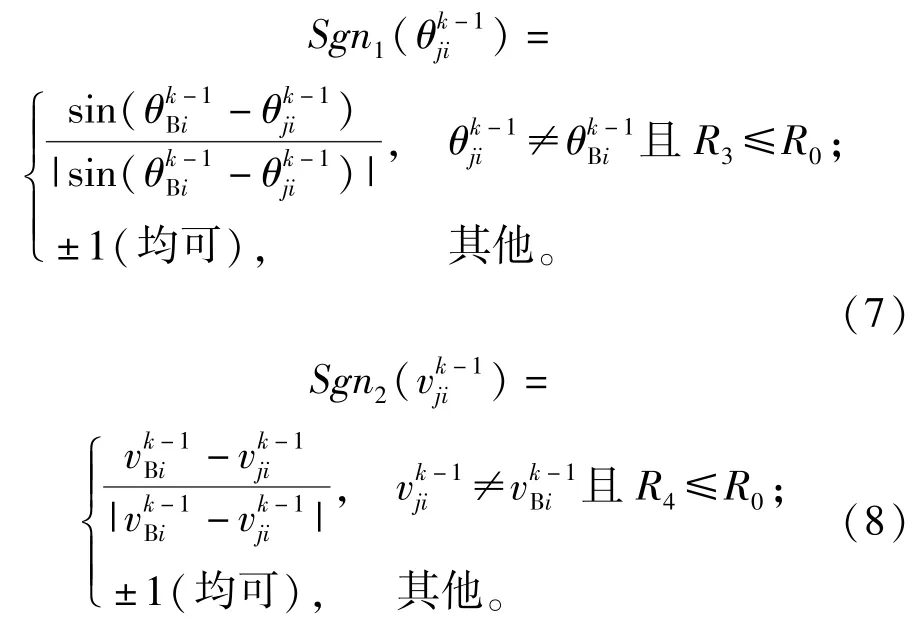
式中:R3和R4为区间[0,1]上的随机数;R0为一个算法参数(0≤R0≤1),用于调节算法在局部搜索和全局搜索间的平衡,本文选取R0=0.8.
通过Sgn(·)得到的基因自适应变异方向,可以使被操作的搜索路径不断向父代最优路径靠近。(7)式的原理为:当π)且R3≤R0时,变异方向取 +1;当[-π,0)∪[π,2π)且R3≤R0时,变异方向取-1;当R3>R0或时,变异方向取±1均可。因此基因θ的方向控制因子Sgn1(·)可简化为(7)式。(8)式的原理更为简单,在此不作赘述。
3.3.4自适应控制因子的分析
依据3.3.2节的3点改进思路,AMGA引入了3个控制因子Sgn、β和γ,设计了自适应变异策略。由(4)式可知,变异操作的方向由Sgn控制,幅度由D、R、β和γ共同控制。
引入方向控制因子Sgn后,算法利用父代最优个体的信息自适应控制变异方向,加快了收敛速度。引入基因位控制因子β后,变异幅度随着基因位的次序线性递增,即在路径中,阶段越靠前,变异幅度越小,保证变异的高效性。引入进化代数控制因子γ后,在进化前期变异幅度大,可以广泛搜索解空间,避免陷入局部最优。在进化后期变异幅度自适应减小,通过对精英个体的微调,提高了变异效率。
总的来说,AMGA的主要优点有:1)通过对变异方向和幅度的自适应控制,提高了变异效率,增强了寻优能力;2)针对父代精英个体组实施变异操作,充分保留了父代有用的遗传信息;3)采用较高的变异概率保证了种群的多样性,有效避免了早熟收敛。因此AMGA在优化过程中由“求泛”到“求精”自适应搜索,兼顾了多样性和高效性,动态调节局部搜索和全局搜索的平衡,使算法收敛速度快、优化结果稳定。
3.4AMGA流程
步骤1 采用双链实数编码方案对染色体进行编码,并初始化种群得到Pop(1),此时进化代数k=1.
步骤3 对算法终止条件的判断。若进化代数k达到最大限制Gmax,终止运算,否则继续进行。
步骤4 按照3.3节的方法对种群Pop(k)进行交叉和变异操作。
步骤5 遗传操作得到的两组新个体组成子代,同时进化代数k←k+1.转至步骤2.
4 仿真验证
4.1算例描述
假设T=0 h时刻,在某海域探测到敌潜艇目标在TS点出水,随后潜入水下,并迅速逃离出水点。我方舰艇获悉情报后,赶往敌情区域展开反潜搜索。依据此背景,分别对目标和搜索者进行具体描述。
首先,讨论目标的运动规则。根据(1)式利用目标起始坐标 TS、速度 vT、方向 θT和阶段时长SteptT(下标T表示目标)对目标加以表达,并利用Monte Carlo方法对目标运动路径进行仿真,其运动规则见图4.(1)式中,速度矢量b(t,X)的方向为θT,其模值为vT.对于表征干扰因素的α(t,X(t))d B(t),仿真中利用一种二维正态噪声Φ代替并作用于目标运动的各个阶段。图4中,目标在第二阶段按照初始航向航速应运动到位置X′(t),由于受到干扰实际运动到位置X(t).
接下来,对目标运动路径进行仿真。已知目标起始坐标为TS=(120 nmile,120 nmile),假定目标的速度vT服从μvT=10 kn,σvT=1 kn的正态分布;阶段时长SteptT服从[1/3 h,1 h]的均匀分布;目标第一阶段方向θ1服从[0 rad,2πrad]的均匀分布,其余阶段方向θi=θ1(i>1).二维正态噪声Φ的均值μΦ1= μΦ2=0nmile,标准差σΦ1=σΦ2= 0.2 n mile,相关系数ρΦ1,Φ2=0.目标路径的仿真次数NT=10 000次,目标分布见图5.
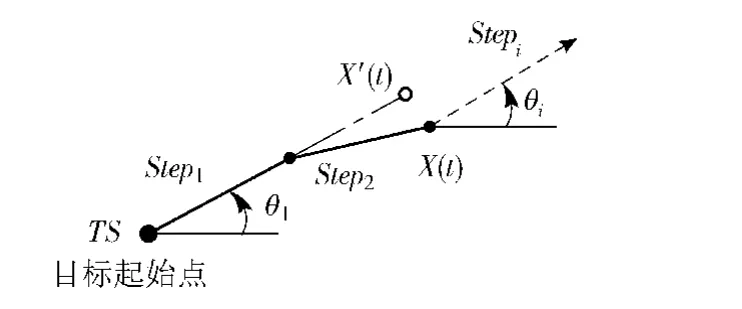
图4 Markovian目标的运动规则Fig.4 Movement rules of Markovian target
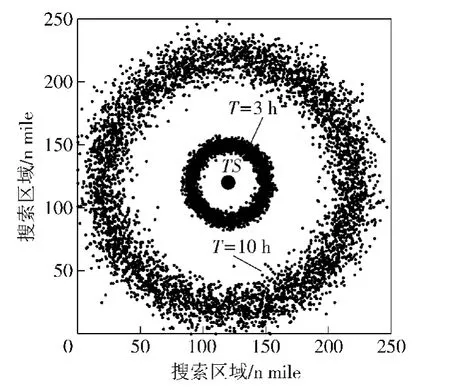
图5 T=3 h和T=10 h时刻目标分布图Fig.5 The distribution of targets at T=3 h and T=10 h
最后,给出搜索者的相关参数。搜索者在T= 0 h时刻展开搜索,起始位置坐标SS=(100 n mile,100 n mile),给定搜索时间Ts=10 h,取各阶段时长Stepts=0.5 h,则阶段总数NStep=20.各阶段方向θs∈[0 rad,2πrad),速度vs∈[10 kn,25 kn],则变量总数为40.在探测方面,声纳作用距离随速度变化的函数 L(vs)见(2)式,探测时间间隔ΔtD= 0.1 h.每条搜索路径CDP的计算公式为
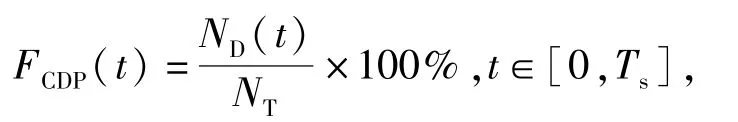
式中:NT为目标仿真的总数;ND(t)为已探测到的目标个数。
4.2算法实现与结果分析
首先,针对仿真算例,给出一个简单的种群初始化方法:初始搜索方案为匀速直线运动,路径方向在SS与TS连线左右各60°的扇面内等间隔选取,初始搜索路径的速度在[10 kn,25 kn]内随机选取,路径分布见图6.
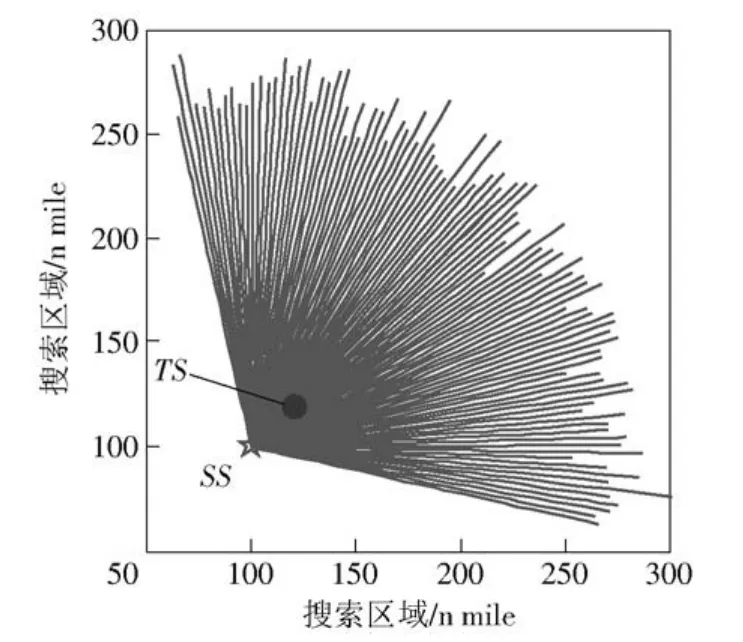
图6 初始搜索方案的路径分布Fig.6 The distribution of initial search paths
然后,利用AMGA求解本算例。设定算法参数为:种群规模M=100,染色体长度N=20,最大遗传代数Gmax=100,精英个体比率PE=0.15,交叉概率PC=0.25,变异概率PM=0.75.在100次独立的仿真实验中,AMGA按照上述初始搜索方案进行运算,最终得到的“最优”搜索路径如图7所示,其累积探测概率FCDP(10)=48.53%,平均速度各阶段速度由(9)式给出(为便于分析已将速度取整):

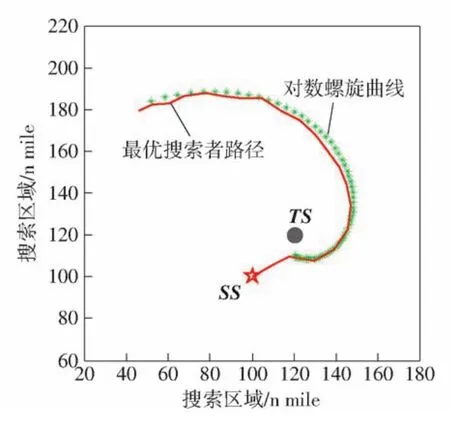
图7 所得最优搜索路径与对数螺旋曲线搜索路径Fig.7 Optimal search path found by AMGA and logarithmic spiral search path
下面对仿真结果进行分析。从AMGA的运算结果可以看出“最优”搜索路径有如下两个特点:
1)搜索速度自动优化调节。算例中,搜索者各阶段速度vs的取值范围为[10 kn,25 kn],速度与探测能力的函数关系由(2)式给出。经AMGA逐步优化,求得的“最优”搜索者路径具有一定的“智能”性:路径各阶段大都没有选择速度最快时的25 kn,也没有选择声呐作用距离L最大时的0~15 kn,而是基本选取了20 kn左右的速度,兼顾了探测能力与速度的大小,反映出AMGA对求解OSPP有较强的优化能力。
2)搜索路径接近于对数螺旋线。在搜索速度固定不变的条件下,对向四周作匀速直线运动的逃离目标这一简单搜索问题,理论上证明了搜索者应采用螺旋搜索方法[21],即搜索路径是一条光滑的对数螺旋线。
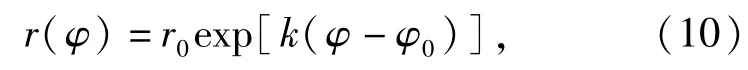
式中:r为螺旋半径;φ为极角;(r0,φ0)为螺旋线开始点;系数k=tan[arcsin(vT0/vs0)],vT0为目标固定的速度,vs0为搜索者固定的速度。本文讨论的是向四周作Markov运动的逃离目标搜索问题,且搜索速度对探测能力有一定的影响,相比上述问题更为复杂,但有相似之处。由AMGA得到的“最优”搜索路径与对数螺旋线比较吻合(见图7),一定程度上表明该算法在求解OSPP上具有较高的有效性。在本例中,(10)式的参数为vT0==10 kn,vs0== 20.3 kn,(r0,φ0)=(10 n mile,-π/2 rad),即方程r(φ)=10exp[0.566·(φ+π/2)].
在实际的搜索问题中,目标的运动复杂多变,搜索者需要根据环境的变化实施灵活的机动。解析方法通常需要利用严格的方程描述问题,应用范围受限。相比而言,AMGA对问题的约束更为宽松,特别是在对搜索双方运动的表达上。因此AMGA在求解连续时空OSPP方面有较大的应用范围和潜力。
4.3算法对比与性能验证
利用AMGA、Cho等[16]提出的GA*和Kierstead等[15]提出的GA#分别求解仿真算例,为使对比效果的可信度更高,3种算法采用相同的种群初始化方法(见4.2节),最大遗传代数Gmax均为100.GA*的参数设置[16]:M=128,PS=0.25,PC=0.125,PM= 0.625.GA#的参数设置[15]:M=120,PS=0.05,PC=0.95×0.9,PClone=0.95×0.1,PM=0.05.以上参数的具体意义请参见相关文献。运算结果见表1.
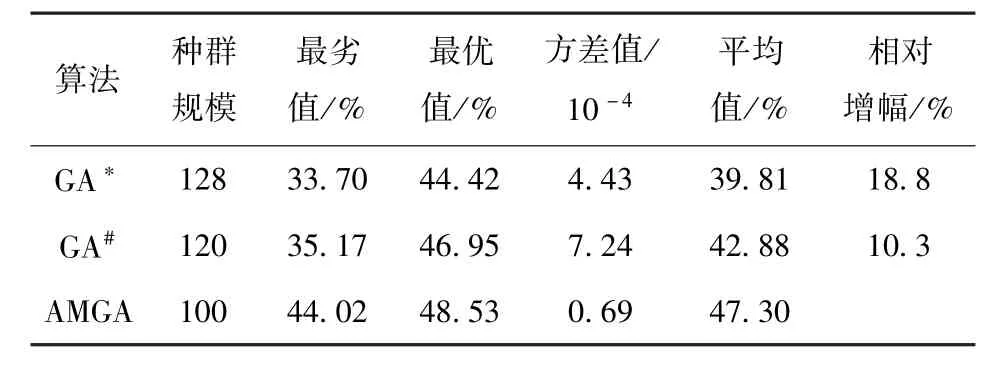
表1 不同算法的结果对比(100次运算)Tab.1 Calculated results of different algorithms (100 calculations)
表1中的种群规模表示算法种群中的个体总数,其值越大,算法往往越易获得更优的结果;最劣值表示算法100次运算结果中最差的累积探测概率FCDP;最优值表示算法100次运算结果中最佳的FCDP;方差值表示算法100次运算结果的方差,其往往能反应出算法的稳定性;平均值表示算法100次运算结果的均值,其可以反映出算法的全局优化能力;相对增幅是指AMGA的平均值指标对于其他算法平均值指标的相对增长幅度。
由表1不难看出,在相同的种群初始化方法下,AMGA种群的数量最少但FCDP的平均值最高,最优值和最劣值相差最小,且FCDP的方差值最小,体现出AMGA较强的全局优化能力和稳定性。在平均值指标上,AMGA相比 GA*、GA#的相对增长幅度为18.8%和10.3%,体现出AMGA显著的性能优势。
图8、图9分别展示了 AMGA、GA*和 GA#100次运算结果中最优的10条搜索路径。由于目标时空分布的对称性,最优的搜索者路径存在两种情况,即搜索方向为顺时针和逆时针。从图8中可以直观地看出,作为一种随机优化算法,AMGA求得了这两种最优路径。同时AMGA的稳定性好,所得路径相似度高,可视为收敛。而图9中,GA*和GA#所得的路径差异相对较大,体现出算法都不够稳定,容易早熟。
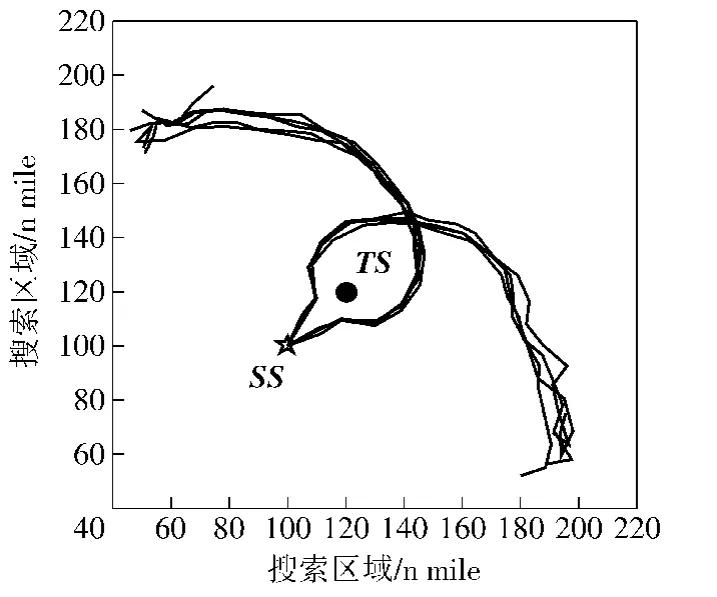
图8 AMGA求得的10条最优搜索者路径Fig.8 10 optimal search paths obtained by AMGA

图9 GA*和GA#求得的10条最优搜索者路径Fig.9 10 optimal search paths obtained by GA*and GA#
因而,AMGA相比GA*和GA#在求解复杂OSPP上,优化效果有明显提高。
5 实例应用
2000年美国科尔号驱逐舰在也门亚丁港遭遇了基地组织的小艇袭击,损失惨重。随后不久,美国海军开始组织多艘小艇攻击舰艇的演习科目[22]。2008年,我国海军开始在亚丁湾索马里海域执行护航任务,护航编队常常需要搜索海盗的快速小艇[23-24]。从上述事件中不难看出,有效地保护一个高价值单元,例如航母、主舰或商船,免受小艇的袭击,是各国海军所面临的一个重要问题[22]。针对这一类问题,Foraker等利用最优控制模型讨论了连续时空多目标搜索问题[25-26],给出了问题的离散化形式及数值求解算法和实例计算结果。本节选用文献[26]中的部分实例,进一步验证AMGA的有效性。
已知在70 n mile×70 n mile的海域上,一艘主舰在t∈[0 h,1 h]内由初始位置(35 nmile,0 nmile)以25 kn的速度沿正北方向匀速航行[22,26]。在此期间,敌方10艘快速小艇间隔1.5 n mile由东侧(70 n mile,6 n mile)~(70 n mile,51.5 n mile)区域进入该海域,并以最短的时间攻击主舰。其中敌目标群进入该海域的初始时间和初始位置服从均匀分布,在驶入前目标作匀速直线运动。为保护主舰安全,直升机由初始位置(23.8 n mile,27.4 n mile)出发,开始执行目标搜索任务(见图10).
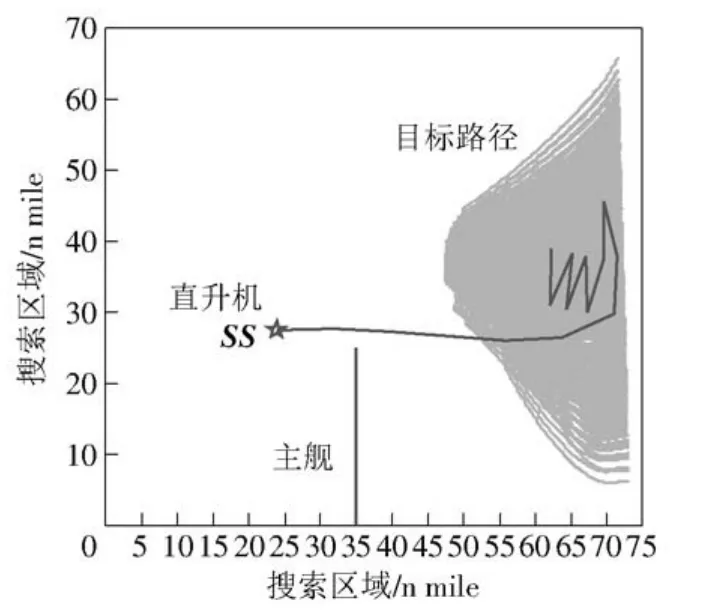
图10 AMGA求得的最优搜索路径Fig.10 The optimal search path found by AMGA
文献[25]建立了最优控制模型,以最小化未发现任何一个目标的概率(记作FP(t))作为目标函数,对搜索路径进行规划,并讨论了计算FP(t)的离散化形式。按照文献[26]建立的目标模型和求解方法[27-28],通过离散化参数空间,实现了不同初始条件的目标仿真(图10展示了部分目标路径),其中目标群进入此海域的初始时间和初始位置的离散化规模均为25,记作δ=(25,25).
下面利用AMGA算法,对搜索路径进行规划。其中搜索时间Ts=1 h,搜索路径的阶段总数NStep= 15,各阶段时长Stepts=1/15 h,搜索速度为120 kn,探测时间间隔为0.01 h.算法的最大遗传代数Gmax=120,其余参数设置与第4节的相同。经50次独立运算,AMGA求得的目标函数均值= 0.023 9,方差为2.8×10-8,其中最佳路径的FP(t)= 0.023 6,即 10艘小艇均未被探测到的概率为0.023 6,最优的搜索路径如图10所示。
由图10可以看出,按照最优搜索策略,直升机先沿直线迅速驶向敌情区域的偏南部分,然后向北搜索,最后在目标可能出现区域的中央反复巡逻,执行搜索和警戒任务,兼顾了不同区域目标的探测。
Foraker等在文献[26]中给出了不同离散化规模δ对应的最优结果FP(t).利用AMGA经10次独立运算求得最优结果,对比如表2所示。
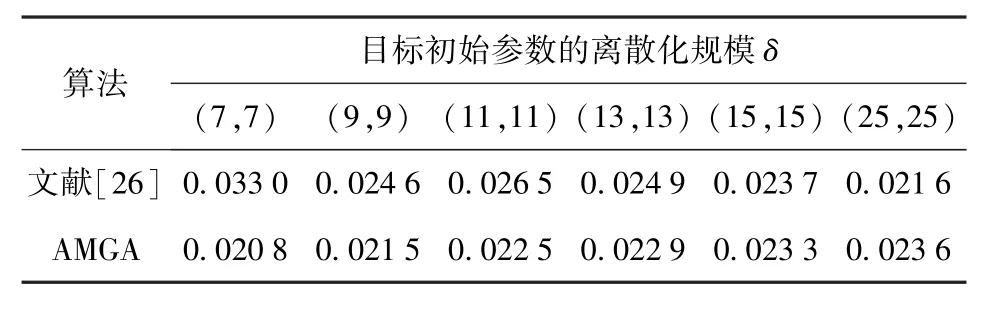
表2 算法对比Tab.2 Comparison between algorithms
需要指出的是,目标路径受初始参数的影响较大,离散化规模的不同会使仿真计算发生变化。通过表2的纵向对比不难看出,在6种不同δ规模下,本文算法有5种结果优于Foraker等[26]求得的最优值,说明了AMGA拥有更好地寻优能力,也适用于求解直升机搜索水面目标的搜索路径规划问题。同时AMGA所得结果方差较小,表明了算法优化能力稳定。
6 结论
本文针对连续时空Markov运动目标的OSPP进行了研究,建立了同时优化搜索者方向和速度的搜索路径规划模型。针对问题特点,设计了一种新颖的AMGA.该算法主要利用对方向和幅度自适应控制的方法改进了变异操作,增强了算法的寻优能力和稳定性,在仿真实验及实例应用中得到了满意的搜索方案,对求解连续时空OSPP具有一定启发意义与应用价值。
(References)
[1]Lavis B,Furukawa T,Durrant-Whyte H F.Dynamic space reconflguration for Bayesian search and tracking with moving targets [J].Autonomous Robots,2008,24(4):387-399.
[2]吴文超,黄长强,宋磊,等.不确定环境下的多无人机协同搜索航路规划[J].兵工学报,2011,32(11):1337-1342. WUWen-chao,HUANGChang-qiang,SONG Lei,et al.Cooperative search and path planning ofmulti-unmanned air vehicles in uncertain environment[J].Acta Armamentarii,2011,32(11):1337-1342.(in Chinese)
[3]Hong SP,Cho S J,Park M J.A pseudo-polynomial heuristic for path-constrained discrete-time Markovian-target search[J].European Journal of Operational Research,2009,193(2):351-364.
[4]Stone L D.What's happened in search theory since the1975 Lanchester prize?[J].Operations Research,1989,37(3):501-506.
[5]Trummel K E,Weisinger J R.The complexity of the optimal searcher path problem[J].Operations Research,1986,34(2):324-327.
[6]Eagle JN.The optimal search for amoving targetwhen the search path is constrained[J].Operations Research,1984,32(5):1107-1115.
[7]Eagle JN,Yee JR.An optimal Branch-and-Bound procedure for the constrained path,moving target search problem[J].Operations Research,1990,38(1):110-114.
[8]Lau H,Huang S,Dissanayake G.Discounted MEAN bound for the optimal searcher path problem with non-uniform travel times [J].European Journal of Operational Research,2008,190(2):383-397.
[9]Sato H,Royset JO.Path optimization for the resource-constrained searcher[J].Naval Research Logistics,2010,57(5):422-440.
[10]Royset J O,Sato H.Route optimization for multiple searchers [J].Naval Research Logistics,2010,57(8):701-717.
[11]Hong SP,Cho S J,Park M J,et al.Optimal search-relocation trade-off in Markovian-target searching[J].Computers&Operations Research,2009,36(6):2097-2104.
[12]杨日杰,吴芳,徐俊艳,等.基于马尔可夫过程的水下运动目标启发式搜索[J].兵工学报,2010,31(5):586-591. YANG Ri-jie,WU Fang,XU Jun-yan,et al.Heuristic search formoving underwater targets based on Markov process[J].Acta Armamentarii,2010,31(5):586-591.(in Chinese)
[13]Ohsumi A.Optimal searching for a Markovian-target[J].Naval Research Logistics,1991,38(4):531-554.
[14]朱清新,卿利,彭博.随机运动目标搜索问题的最优控制模型[J].控制理论与应用,2007,24(5):841-845. ZHU Qing-xin,QING Li,PENG Bo.Optimal control model of search problem for randomly moving targets[J].Control Theory &Applications,2007,24(5):841-845.(in Chinese)
[15]Kierstead D P,DelBalzo D R.A genetic algorithm applied to planning search paths in complicated environments[J].Military Operations Research,2003,8(2):45-59.
[16]Cho JH,Kim JS,Lim JS,et al.Optimal acoustic search path planning for sonar system based on genetic algorithm[J].International Journal of Offshore and Polar Engineering,2007,17 (3):218-224.
[17]Cho JH,Kim JS.Benchmarking of optimal acoustic search path planning[C]//Proceedings of the 19th International Offshore and Polar Engineering Conference.Osaka,Japan:International Society of Offshore and Polar Engineers,2009:620-626.
[18]厄克森达尔B.随机微分方程导论与应用[M].第6版.刘金山,吴付科,译.北京:科学出版社,2012. Oksendal B.Stochastic differential equations[M].6th ed.LIU Jinshan,WU Fu-ke,translated.Beijing:Science Press,2012.(in Chinese)
[19]瓦格纳D H,迈兰德W,森德T J.海军运筹分析[M].第3版.姜青山,郑保华,译.北京:国防工业出版社,2008:207-212. Wagner D H,Charles Mylander W,Sanders T J.Naval operations analysis[M].3rd ed.JIANGQing-shan,ZHENG Bao-hua,translated.Beijing:National Defense Industry Press,2008:207-212.(in Chinese)
[20]李敏强,寇纪淞,林丹,等.遗传算法的基本理论与应用[M].北京:科学出版社,2002. LIMin-qiang,KOU Ji-song,LIN Dan,et al.The basic theory and applications of genetic algorithm[M].Beijing:Science Press,2002.(in Chinese)
[21]李乃奎,崔同生.军事运筹学基础理论教程[M].北京:国防大学出版社,2005. LINai-kui,CUI Tong-sheng.Basic theory of military operation research[M].Beijing:National Defense University Press,2005. (in Chinese)
[22]Foraker J.Optimal search for moving targets in continuous time and space using consistent approximations[D].Monterey,California:Naval Postgraduate School,2011.
[23]肖洋,柳思思.索马里海盗的“恐怖主义化”及对策[J].当代世界,2010(1):57-59. XIAO Yang,LIU Si-si.“Terrorism”of Somalipirates and countermeasures[J].The Contemporary World,2010(1):57-59. (in Chinese)
[24]邵哲平,潘家财.亚丁湾水域交通特征分析及防海盗策略研究[J].中国航海,2011,34(4):119-122. SHAO Zhe-ping,PAN Jia-cai.Analysis of the Gulf of Aden's traffic characteristics and study of anti-piracy strategy[J].Navigation of China,2011,34(4):119-122.(in Chinese)
[25]Foraker J,Royset J O,Kaminer I.Search-trajectory optimization:part I,formulation and theory[J/OL].Journal of Optimization Theory and Applications,2015.doi:10.1007/s10957-015-0768-y.
[26]Foraker J,Royset J O,Kaminer I.Search-trajectory optimization:part II,algorithms and computations[J/OL].Journal of Optimization Theory and Applications,2015.doi:10.1007/ s10957-015-0770-4.
[27]Yakimenko O.Directmethod for rapid prototyping of near-optimal aircraft trajectories[J].Journal of Guidance,Control,and Dynamics,2000,23(5):865-875.
[28]Ghabcheloo R,Kaminer I,Aguiar A,et al.A general framework formultiple vehicle time-coordinated path following control[C]∥American Control Conference.St Louis,Missouri,US:the American Automatic Control Council,2009:3071-3076.
Research on Optimal Search Path Programm ing in Continuous Time and Space Based on an Adaptive Genetic Algorithm
ZHANG Xian,REN Yao-feng,WANG Run-peng
(College of Science,Naval University of Engineering,Wuhan 430033,Hubei,China)
A Markovian-targetmodel based on stochastic differential equations and a path programming modelwith both searcher's direction and velocity treated as decision variables are presented for optimal searcher path problem in continuous time and space,and the effectof searcher's velocity on the detection ability is considered.A genetic algorithm with adaptivemutation is designed by introducing three kinds of control factors,which fulfills the adaptive control of the direction and range ofmutation and dynamically regulates the balance between local search and global search.In an example of searching a targetwith a random escaping direction,an approximate logarithmic spiral path is found.Moreover,the algorithm provides a reasonable and effective search scheme in a path programming problem for a helicopter searching multiple targets.The results indicate that the proposed algorithm has the significantadvantages of stability and global optimizing ability in comparison with othermethods,and is well suitable for the search path programming problem in continuous time and space.
operations research;optimal search;continuous time and space;Markovian target;genetic algorithm with adaptivemutation;anti-submarine search
O229;E917
A
1000-1093(2015)12-2386-10
10.3969/j.issn.1000-1093.2015.12.024
2014-09-03
全军军事学研究生课题(2011JY002-423)
张献(1990—),男,博士研究生。E-mail:919453887@qq.com;任耀峰(1959—),男,教授,博士生导师。E-mail:renyaofeng@sina.com
