矩阵式双向变流器改进型换流策略
2015-09-17叶曙光邓海波李林文戴卓强
刘 钊,叶曙光,张 倩,邓海波,李林文,戴卓强
(1.南京电子技术研究所,江苏 南京 210039;2.江苏金思源电力科技有限公司,江苏 南京 210018;3.上海电力股份公司吴泾热电厂,上海 200241)
0 引言
可再生能源(如光能、风能等)具有间歇性、不稳定性的特点,故需要储能装置解决可再生能源发电系统与电力负荷的供需不平衡问题,从而提高可再生能源发电系统运行稳定性[1-2]。双向变流器作为电网与储能电池之间的连接枢纽,具有相当重要的研究意义。与传统的三相桥式脉宽调制(PWM)型变流器相比,矩阵式双向变流器同样能够实现输入电流正弦、功率因数可调、能量双向流动等功能,此外其为Buck型降压整流器,能够实现降压功能,电压调节范围大,在0 V到1.5倍的相电压幅值内连续可调,而三相桥式变流器为Boost型升压整流器,因此矩阵式双向变流器能够实现一级变换,省掉中间直流环节,结构紧凑,体积小,功率密度大,更适合于液流电池等低压蓄电池场合[3-4]。
目前矩阵式变换器工业产品的最高容量为200 V/63 kW和400 V/114 kW,限制其大功率应用的主要原因在于开关管较多、成本高、安全可靠的换流算法以及大功率变流器的电磁兼容设计等。换流是矩阵式双向变流器正常工作的必要条件之一,换流的原则是在保证安全换流的前提下,不使硬件开销过大,同时尽可能减小对调制策略、输入电流和输出电压的影响。国内外许多文献提出了各种换流策略[5-9],归纳起来可分为基于输出电流方向的电流型换流策略和基于输入相电压的相对大小的电压型换流策略。由于矩阵式双向变流器的输出电流为直流,方向固定,只有在整流和逆变工作状态切换的时候才会出现电流方向改变,电流型换流方法更适合于这种场合。常用的电流型换流策略有四步换流、三步换流、两步换流等[10-12],换流步数较多时,特别是在低调制比区域,换流过程引起的输出电压误差相对于直流输出电压较大,通常功率等级越大,开关管的开通与关断时间越长,此种情况下减小换流步数显得更为重要。
文献[13]采用一种电压电流型一步换流方法,能够实现安全换流,但输入相电压相对大小判断不准确时会因为输入相导通错误使输入电流波形畸变。本文对此进行了详细分析,并提出利用输入电流扇区的划分方法来判断输入电压的相对大小,在可能出现大小相等的电压相之间采用两步换流,其他情况下采用一步换流的方法,并根据仿真和实验对所提换流策略进行了验证。仿真和实验结果表明,该方法不需要外加专门的精确检测输入相电压相对大小关系的测量装置,即可实现矩阵式双向变流器安全、可靠、快速换流和稳定运行,且输入电流波形不受影响。
1 矩阵式双向变流器基本原理
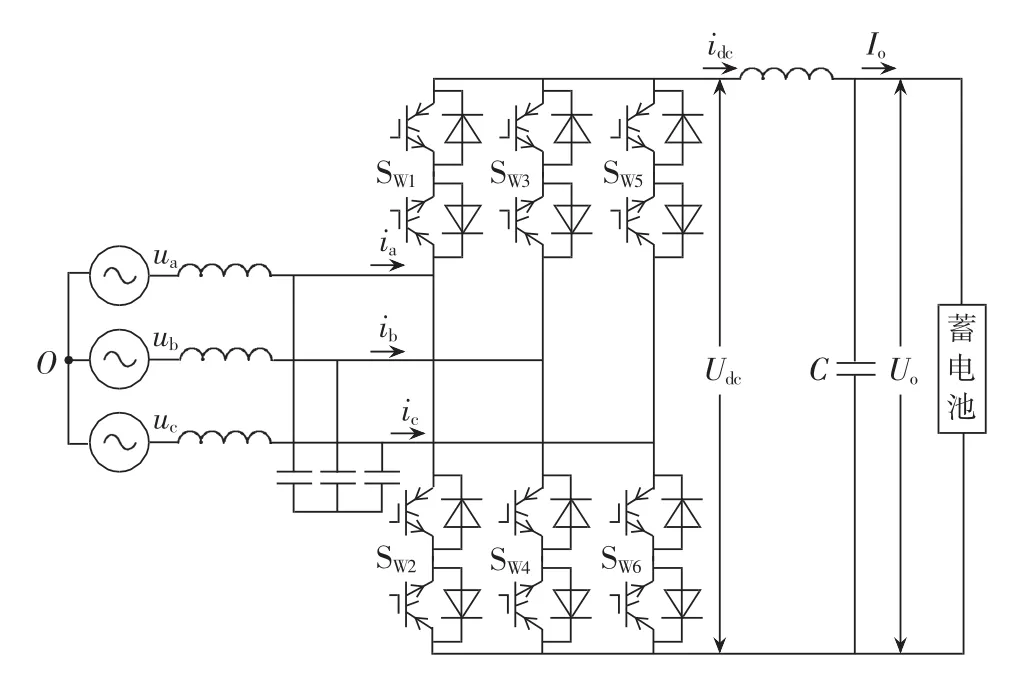
图1 矩阵式双向变流器主电路图Fig.1 Main circuit of bidirectional converter based on matrix converter
图1为接电池负载的矩阵式双向变流器主电路图,双向开关由2个IGBT组成,方向可控。其中,ua、ub、uc为网侧输入相电压;ia、ib、ic为输入相电流;Udc、idc分别为变换器侧输出直流电压和直流电流;Uo、Io分别为电池端电压和端电流。
对于储能电池而言,无论是以恒压、恒流还是恒功率作为充放电方式,其落脚点都是控制电池的端电压和端电流,因此充放电模式下对矩阵式双向变流器的输出电压和输出电流的控制示意图如图2所示。其中,为指令充放电电池电压;为指令充放电电池电流;θu为期望功率因数角;φs为电网电压相位角;mu为电压调制比;Gcu、Gci分别为电压和电流调节控制器。
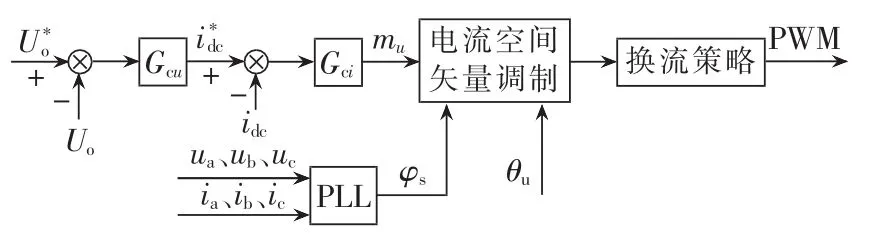
图2 矩阵式双向变流器控制框图Fig.2 Control of bidirectional converter based on matrix converter
矩阵式双向变流器的每相输出与多相输入经双向开关连接,双向开关必须满足输入不短路、输出不断路的原则[14-17],因此双向可控开关的安全换流是在矩阵式双向变流器应用于实际系统中最重要的一个环节[18]。
2 电压电流一步换流策略
电压电流混合型一步换流策略是利用输入电压相对大小的判断,每个主开关状态预导通辅助开关管,从而省去电流型两步换流中的第一步,实现一步换流。根据输入电压相对大小将三相输入电压划分为6个电压扇区,如图3(a)所示,每个扇区内三相电压大小明确,定义输入电压最大相为up、中间相为um、最小相为un,则3种输入相电压接通输出端时的主开关状态如图3(b)所示,其中二极管表示开关管仅开通导通电流方向开关管。由于预导通了开关管,3种主开关状态间的切换仅需一步就能实现。但当输出电流方向改变时,由于需要先关断预导通的顺管才能开通反向的逆管,因此电流方向切换时需要4步实现。开关状态图如图4所示,图中的六位数字分别表示输出一相连接到输入三相a、b、c的双向开关,“1”表示开通,“0”表示关断。 如:“001001”表示输出相连接到输入a相的2个开关均关断,连接到输入b相的开关顺管导通、逆管关断,连接到输入c相的开关顺管关断、逆管导通。在图4所示一步换流逻辑状态图中,当i>0时,假设ua>ub>uc,则ua=up,ub=um,uc=un。 此时,从 a 相切换到 c 相的开关顺序是同时关断a相和b相的开关顺管,输入电流由a相切换到c相,换流过程为强制换流;从c相切换到a相的开关顺序是同时开通a相和b相的开关顺管,输入电流由c相切换到a相,换流过程为自然换流。同理其他状态下各相之间的切换逻辑均类似。
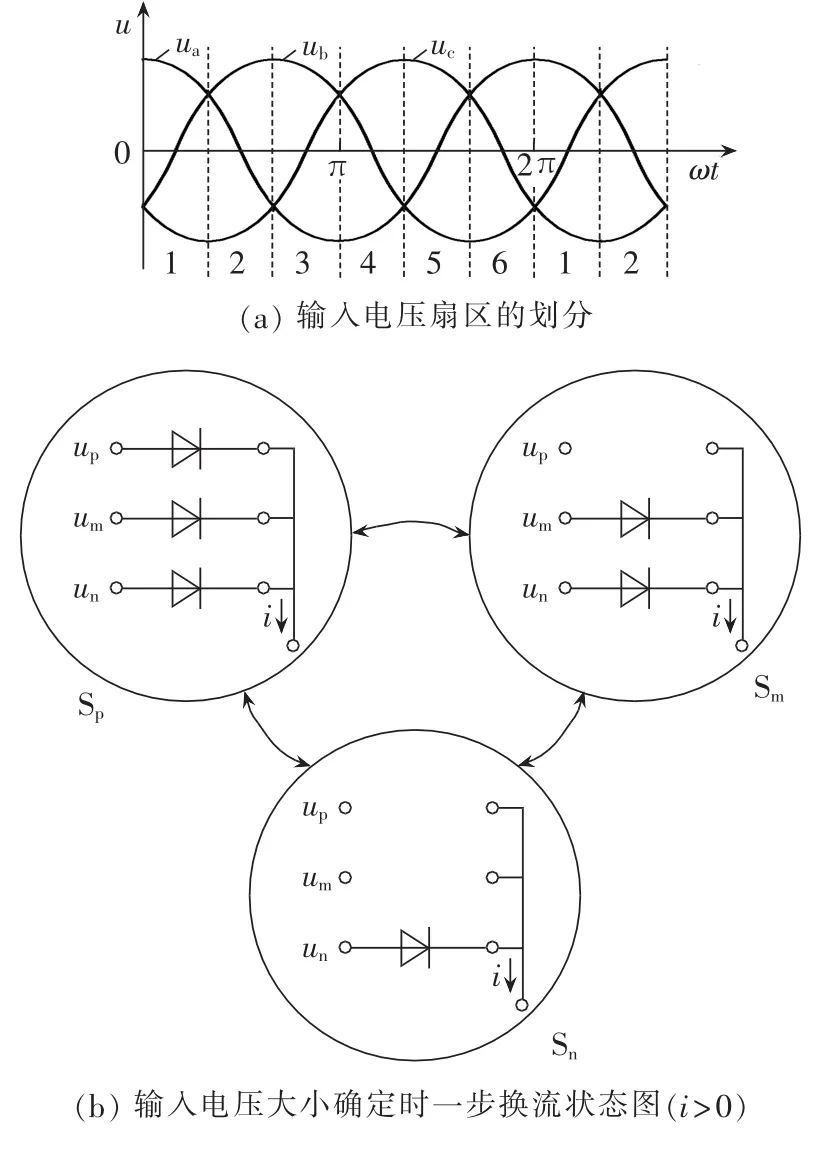
图3 电压扇区划分及一步换流主开关状态Fig.3 Voltage-sector division and main switch states of one-step commutation
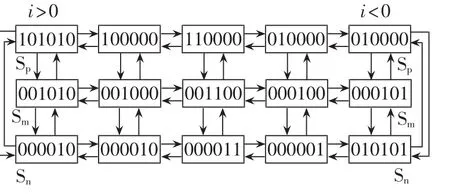
图4 电压电流型一步换流状态图Fig.4 State diagram of current-voltage one-step commutation
电压电流型一步换流策略实现的前提条件是需要知道当前时刻输出电流方向以及所在的电压扇区。在三相电压对称、没有谐波并且锁相准确的情况下,理论上可以根据划分好的电压扇区来实现一步换流策略。但由于输入电压中存在着谐波、采样误差以及三相电压不平衡等原因,实际中仍然是根据三相输入电压的大小来判断扇区,而在相邻扇区切换时,因为三相电压中的两相电压大小相近容易造成扇区判断错误,使PWM周期中所使用的有效矢量不是期望的有效矢量,最终导致输入电流畸变。
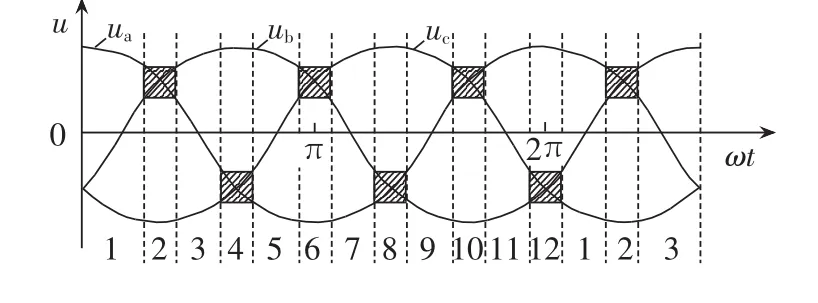
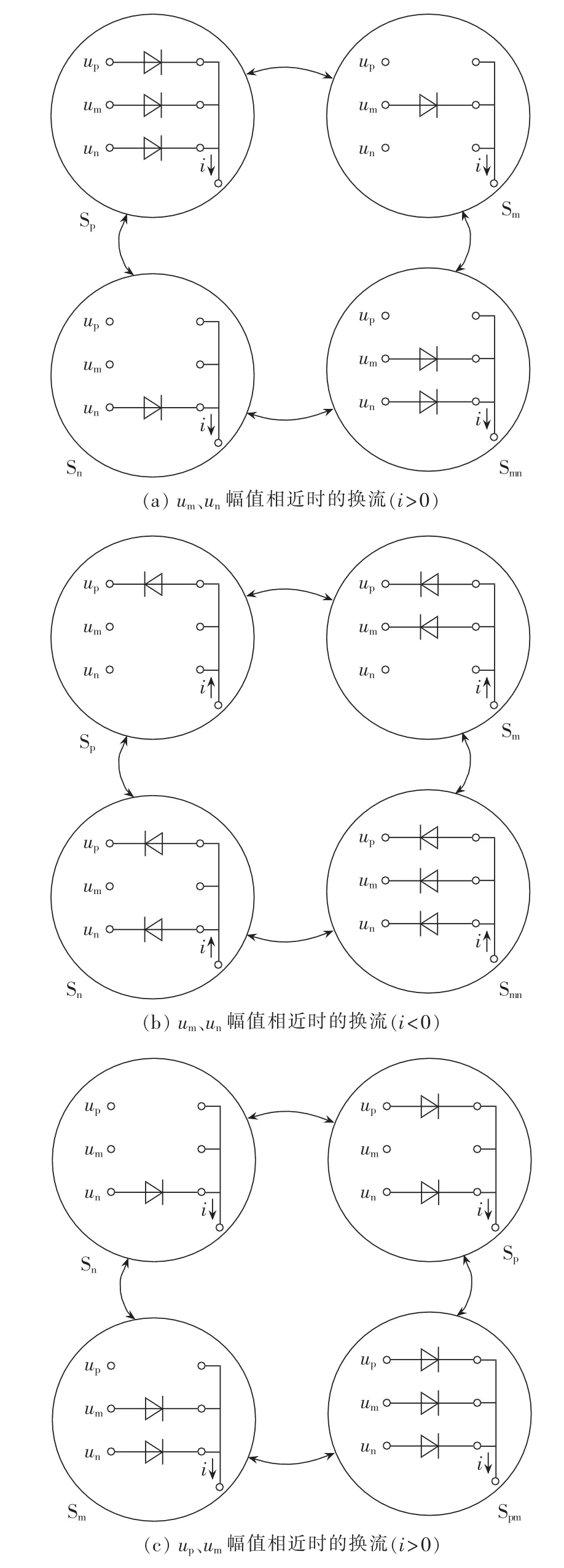
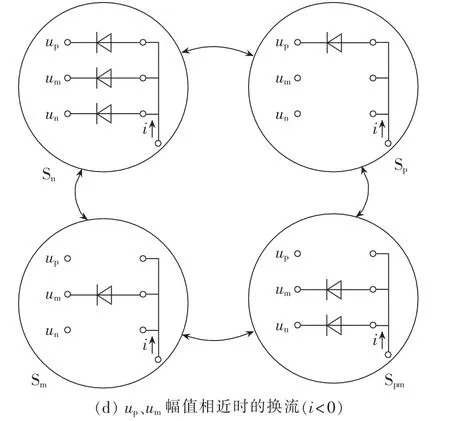
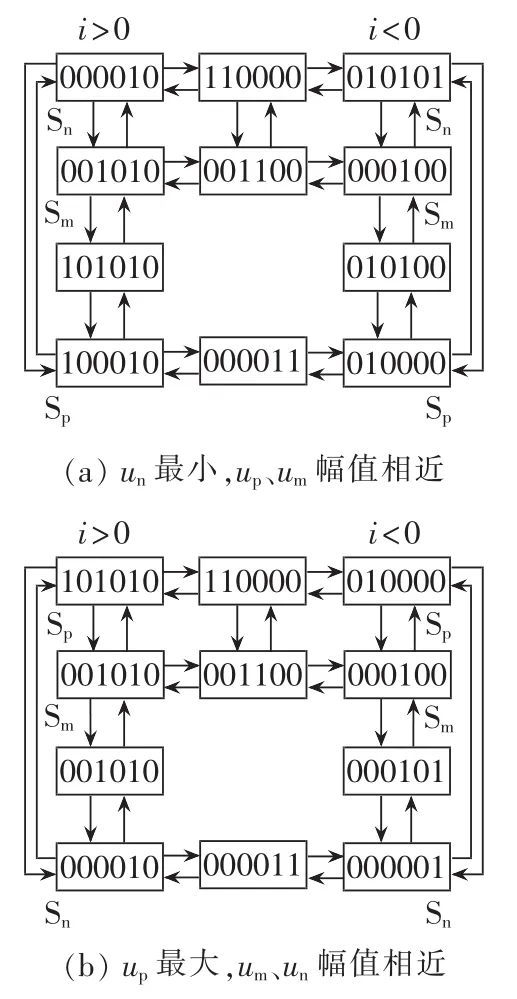
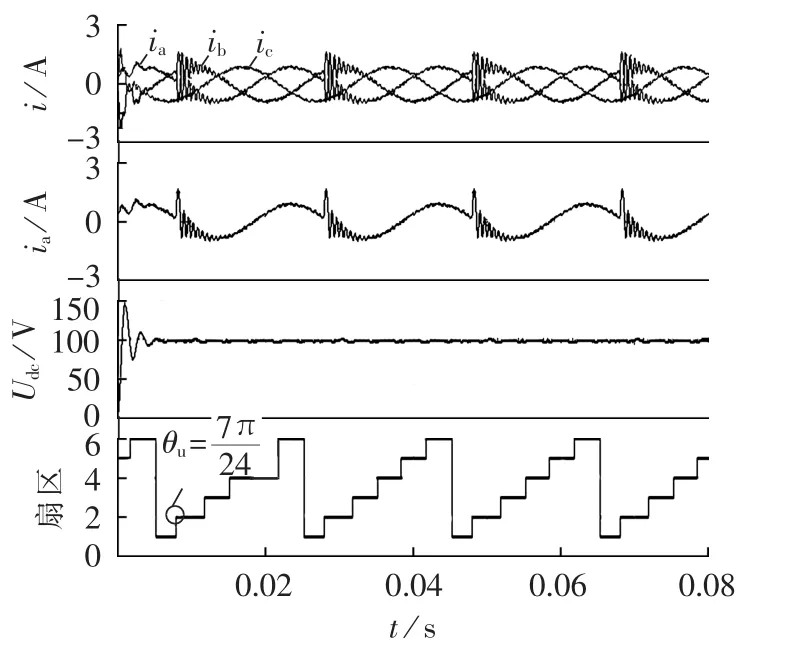
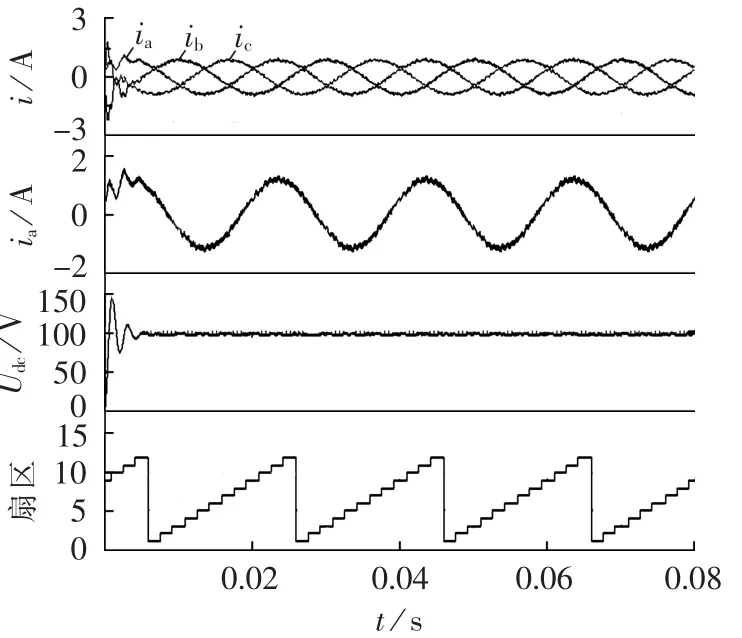
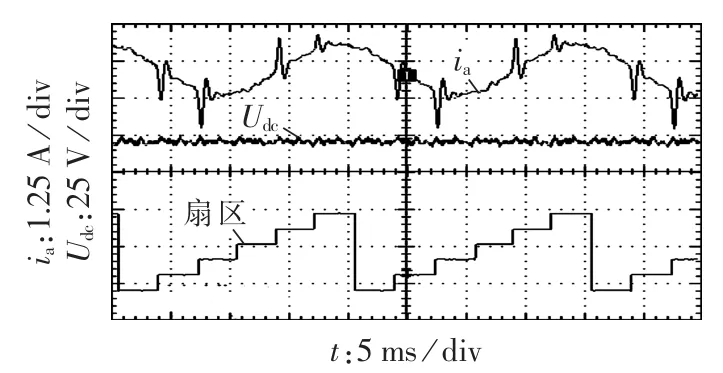
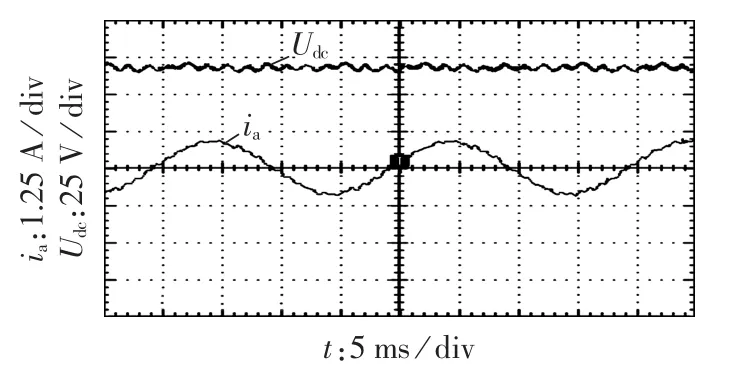
以图3中的输入电压扇区1为例,在扇区1与扇区2交界处,ua与ub大小相近,会出现检测不准确的情况。 假设此时为扇区 1,ua>ub>uc,ua=up,ub=um,uc=un,输出接 a相时为“101010”,输出接 b相时为“001010”,输出接 c 相时为“000010”;假如检测结果为 ub>ua>uc,ub=up,ua=um,uc=un,输出接 a 相时为“100010”,输出接 b 相时为“101010”,输出接 c 相时为“000010”。此时电压差值较大两相间进行切换时,如a相切换到c相,直接关断a相顺管即完成换流;b相切换到c相,同时关断a、b相顺管即可正确换流。而相近电压相之间进行换流时,如a相切换到b相,直接开通b相顺管即可,但由实际电压大小(ub 图5 扇区1内输出电压时序图Fig.5 Timing diagram of output voltage in sector 1 为解决输入电压扇区检测错误导致输入电流波形畸变的问题,提出采用“过渡区间”的方法,对输入电压区间重新划分,将输入电压相近两相采用两步换流。如图6所示,将输入三相电压相对大小明确的区域命为主区间,两相电压相近的区间定义为过渡区间(见阴影框部分),在主区间内采用图3中的一步换流,过渡区间内,电压差值较大的两相采用一步换流,而差值较小的两相采用图7中的两步换流,换流的原则是不允许输入相不确定的状态出现。该方法能够有效解决扇区判断不准确导致输入电流畸变的问题。由图6可知,过渡区间出现在相邻扇区的交界点处,即线电压的过零点位置。设置过渡区间时,首先应当保证在过渡区间内检测电路能够准确判断三相输入电压的大小,因此过渡扇区的宽度要大于采样输入电压的纹波,例如当经过电压霍尔采样到的输入电压纹波大小为ur时,则此时过渡区间的宽度应该设置为至少大于ur;其次如果过渡区间过宽,相邻扇区切换时采用的两步换流次数越多,也会影响到输入电流波形。因此过渡区间宽度的设置原则为:在能够准确判断出输入相电压之间的相对大小下尽可能地小。 图6 主区间与过渡区间的划分Fig.6 Division of main and intermediate intervals 图7 不同电流方向下三相输入电压间的换流Fig.7 Commutation among three-phase voltages under different current directions 图8为改进型一步换流过程开关状态图,例如在图8(b)中,当 i>0 时,假设 ua为最大相(ua=up),ub和uc幅值相近,那么a相和b相、a相和c相之间的切换均为一步换流。假设ub>uc,从输入b相切换到输入c相的开关顺序是先开通c相顺管,此时c相顺管开通对变换器无影响,然后关断b相顺管,输入电流由b相切换到c相,换流过程为强制换流;如果ub 图8 换流过程开关状态图Fig.8 State diagram of switch during commutation 利用MATLAB/Simulink构建矩阵式双向变流器仿真模型,仿真条件:输入线电压有效值200 V,电阻负载36Ω,调制周期200μs(开关频率5kHz),调制比mu=0.6,输入滤波电感1mH,输入滤波电容10μF,输出滤波电感5 mH,输出滤波电容20 μF。 图9为电压电流型一步换流仿真结果,图中给出了输入三相电流波形、输出直流电压波形以及输入电压扇区。由仿真波形可以看出在扇区切换的位置,每个调制周期进行一次电压扇区判断,存在一定的误差,使得调制周期内输出相与输入相接通错误从而导致输入电流波形畸变,但由于每个调制周期输出电压平均值没有改变,因而输入电压扇区的判断错误不对输出电压造成影响。 图9 电压电流型一步换流下变换器仿真波形Fig.9 Simulative waveforms of current-voltage one-step commutation 图10为改进型电压电流型一步换流仿真结果。 图10 改进型电压电流型一步换流仿真波形Fig.10 Simulative waveforms of improved current-voltage one-step commutation 过渡区间的宽度设置为π/6。从仿真可以看出,整个波形中不再出现电流波形畸变的情况,通过设置过渡区间,能够有效避免因为输入电压大小判断错误导致的输入相与输出相接通错误造成输入电流波形畸变的情况,证明了换流策略的有效性。 在仿真的基础上,搭建了实验样机对矩阵式双向变流器带蓄电池负载进行了性能测试。实验条件与仿真条件相同,采用DSP TMS320F28335与FGPA EP2C8为控制核心,由运算能力较强的处理器DSP实现矩阵式双向变流器的调制策略,换流策略逻辑性较强,用FPGA实现较为容易。该实验样机由12只英飞凌1200V/40A分立IGBT器件IKW40N120T2构成,首先通过估算IGBT损耗计算出其热阻,然后根据热阻选择散热器表面积,再通过散热器厂家提供的手册选择合适形状的散热器及长度,设计时会考虑一定裕量。12只IGBT均匀布置在散热器上,散热器左右两侧均有风机,一侧吹风,另一侧抽风。实验中通过带额定5kW负载连续工作3h,散热器上温度达到稳定,最高温升不超过30℃,满足设计要求。 图11为电压电流型一步换流实验波形,图12为改进型电压电流型一步换流实验波形,实验结果与仿真结果基本一致,进一步验证了所提换流策略的有效性。 图11 电压电流型一步换流实验波形Fig.11 Experimental waveforms of currentvoltage one-step commutation 图12 改进型电压电流型一步换流实验波形Fig.12 Experimental waveforms of improved current-voltage one-step commutation 本文对矩阵式双向变流器电压电流混合型一步换流策略进行了分析,详细研究了电压电流型一步换流中存在的问题,并提出了在过渡区间采用两步换流的改进型换流策略。该换流策略不需要外加专门的精确检测输入相电压相对大小关系的测量装置,能够有效解决输入电压大小判断错误时输入电流波形畸变的问题。通过仿真和实验对所提换流策略进行了验证,仿真和实验结果证明了所提方法的有效性。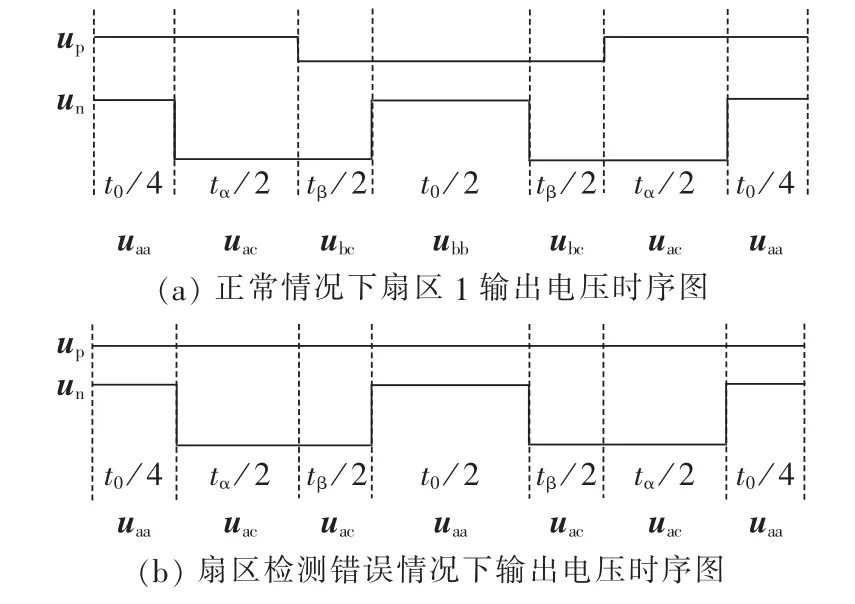
3 改进型一步换流策略
4 仿真及实验结果
5 结论
