基于合作博弈和云模型的变压器状态评估方法

2015-09-17徐岩，陈昕

电力自动化设备 2015年3期

徐岩，陈昕

（华北电力大学电气与电子工程学院，河北保定 071000）

0 引言

变压器是电力系统中最重要的电气设备之一，长期以来，电力系统对变压器均采取定期检修的方式，然而当变压器处于健康状态时，这种方式会造成检修过度。状态检修[1-2]是近年来提出的一种检修方式，即对变压器的运行状态及时地进行检修。因此从定期检修转向状态检修是电力系统发展的必然趋势，这就要求准确地进行变压器状态评估[3-5]。

变压器状态评估的重要目的是准确地评估出变压器当前的健康状态，从而进一步研究可能会发生故障的点，为变压器状态检修提供必要的指导信息。近年来，国内外学者对变压器状态评估进行了研究，引入了证据推理法[6]、关联规则[7]、支持向量回归[8]、模糊理论[9]等方法。文献[9]采用模糊理论建立了综合评判模型，较全面地考虑了影响变压器运行的因素，但是在确定权重时仅采用层次分析法，无法避免单一权重导致的权重精确度偏差，并且忽视了固定权重无法客观反映个别关键参数严重偏离正常值时对变压器运行状态带来的影响。文献[10]在文献[9]的基础上提出采用变权模式，与常权相比更能反映变压器的真实运行状态，但在评价模型中只考虑到事物不确定性中的模糊性而忽略了随机性。

为了解决文献[9-10]提出方法所存在的问题，本文借鉴合作博弈确定组合权重的方法计算固定权重，以协调不同权重确定方法的不一致关系，有利于避免单一权重导致的指标权重精确度偏差，采用变权公式结合实际数据对固定权重进行修正，采用云模型函数代替模糊隶属度函数求取定量评估指标对变压器运行状态的隶属度，建立变压器状态分层评估模型，提出了基于合作博弈确定组合权重和云模型的变压器状态评估方法。

1 变压器状态评估指标体系

变压器状态评估涉及因素众多，而且各个因素的影响程度均不相同，只有综合考虑变压器的各种影响因素，才能够反映变压器的整体性能，进行科学的评价。然而由于技术水平的限制，很难利用所有的试验项目进行评估。另外，不同的运行条件也会对变压器缺陷的发展趋势造成差异。因此本文从试验记录、运行记录和历史记录中选取具有代表性的评估状态量，构建变压器状态评估指标体系如图1所示。指标体系由目标、项目、子项目和指标4个层次构成。U是目标层，表示变压器运行状态的评估结果，下面细分为若干评估项目；U1、U2、U3构成项目层，表示变压器状态的评估因素，是从不同方面对目标层的具体描述；U11、U12、U13是试验记录项目层的 3个子项目；指标层是（子）项目层的细化，表示变压器的具体评估状态量。

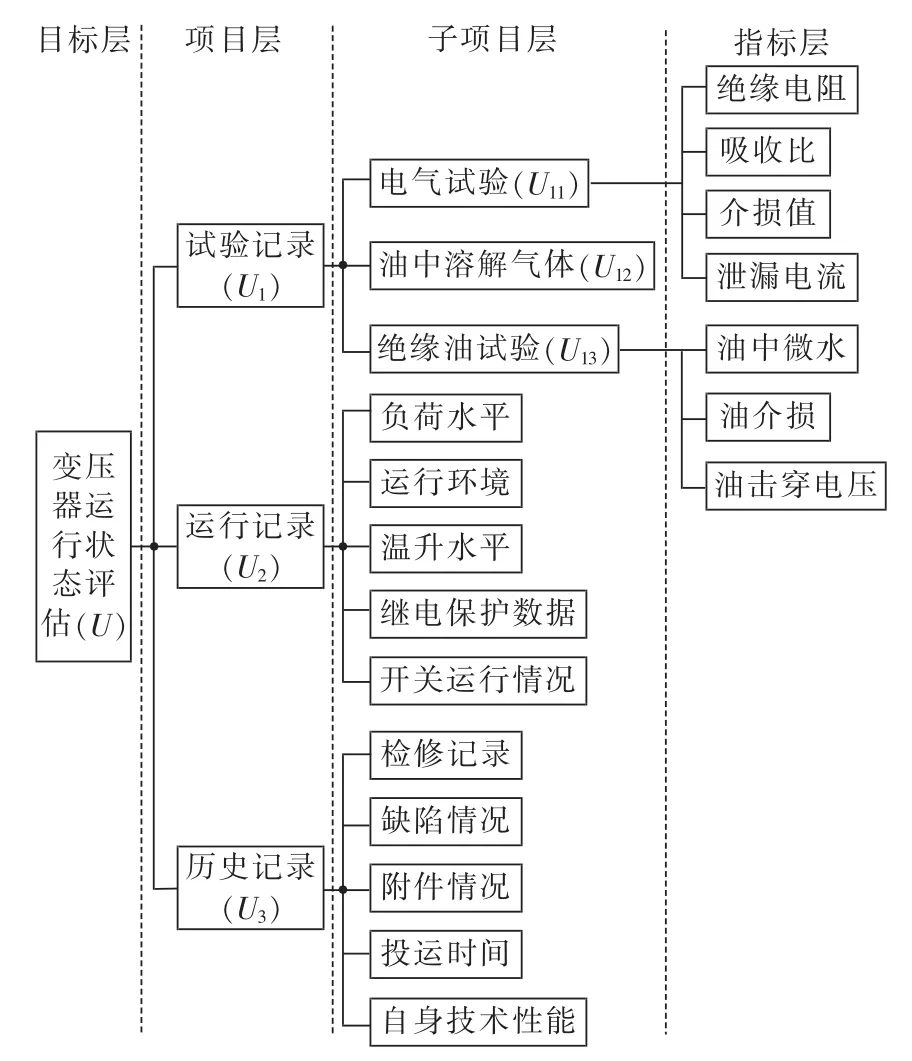
图1 变压器状态评估指标体系Fig.1 Transformer state assessment index system

2 确定变压器指标组合权重的合作博弈方法

变压器指标权重的确定一直都是变压器状态评估的一个难点，目前学术领域主要提出熵权法[11]、层次分析法[12]和神经网络法[13]等。熵权法属于客观赋权法，具有严格的数学意义，但往往会忽视专家经验在某些定性指标中的作用。层次分析法属于主观赋权法，通过两两比较的方法确定各因素的相对重要性，然后由专家打分确定各个指标的权重，易陷入专家意见的主观性局限。BP神经网络属于智能赋权法，通过对样本的自主学习获得各个指标的权重，偏向于依赖合适的样本和初始参数设置。为了避免单一权重导致的指标权重精确度偏差，本文引入一种基于合作博弈的组合权重确定方法。

基于合作博弈确定组合权重[14]的基本思想是：将若干种确定权重的单一方法结成联盟，作为一个整体采取合作博弈的思想确定组合权重，尽量提高组合权重的精确度。该方法的输入为分别用不同的方法 i（i=1，2，…，m）计算出的指标权重 W（i），输出为m种权重的组合权重W，具体步骤如下。

a.计算 W（i）与 W（m_i）的一致性相关系数 Li。

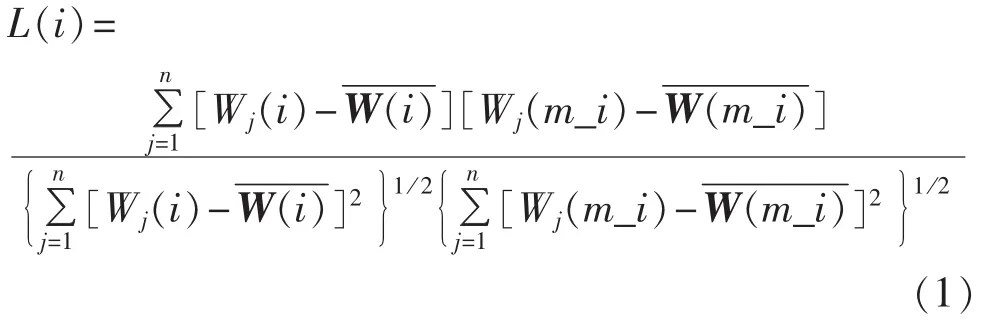
其中，Wj（i）为使用第i种方法计算的第j个指标的权重；W（m_i）为除 W（i）外的 m-1 种权重 W（1）、…、W（i-1）、W（i+1）、…、W（m）的组合权重；n 为权重中指标的个数；“—”表示求平均值。

b.求取组合权重W′：

c.由于 W（m_i）为除 W（i）外的 m-1 种权重的组合权重，所以与求m种权重的组合权重W′的方法一样，可以采用递归调用，每调用一次权重个数减1，直到权重的个数等于2为止。

d.权重个数等于2时，W′的计算公式为：

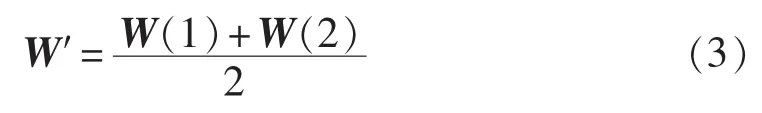
e.将W′归一化得到W。以图1中的目标层为例计算U的组合权重。分别采用熵权法、层次分析法和BP神经网络法计算U的指标权重：

3种单一计算权重的方法详见文献[11-13]。

对于指标权重 W（1），根据式（3）计算 W（2）与W（3）的组合权重 W（3_1）：

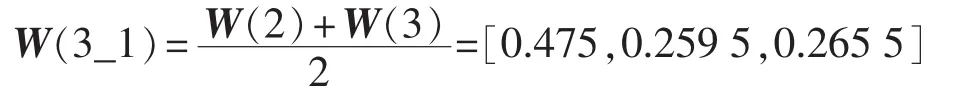
根据式（1）计算 W（1）与 W（3_1）的一致性相关系数：

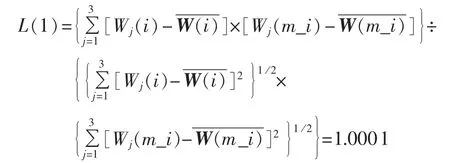
同理根据式（3）和式（1）计算 L（2）、L（3），可得L（2）=0.9485，L（3）=0.9664。

根据式（2）计算组合权重W′：

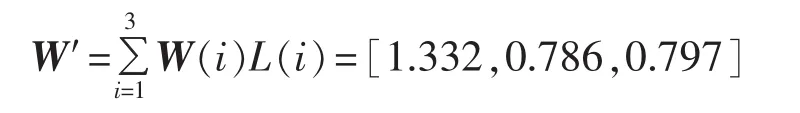
对 W′进行归一化处理得 W=[0.457，0.270，0.273]。

同理，利用MATLAB7编程进行计算，能够分别得到图1中U2、U3的组合权重。

3 确定评判矩阵的云模型方法

对于电气试验和绝缘油试验中各定量评估指标，广泛采用相对劣化度[12]来获取模糊隶属度函数，然后确定定量评估指标对变压器状态的隶属度，从而得到评判矩阵。这样仅考虑了事物不确定性中的模糊性而忽略了随机性。因此本文采用云模型代替模糊隶属度函数，兼顾模糊性与随机性，以求更接近实际的评判矩阵。

云模型[15]是自然语言表示的能够实现定性概念与定量数值之间的不确定性转换的模型，其具有3个数字特征 Ex、En、He。 Ex为期望，代表空间中最能表达这个定性概念的点；En称为熵，常被用作衡量定性概念的模糊度与概率，反映定性概念的不确定性；He为超熵，它是熵的不确定性的度量，即熵的熵，反映数域空间中代表该语言值的所有点的不确定度的凝聚性，即云滴的凝聚度。云模型可以用来表达变压器中定量评估指标与定性描述之间的转换过程，这样兼顾了事物不确定性中的模糊性与随机性。

文献[16]中指出指标j和等级c这一定性概念间的转换可以用云模型表示，其云特征值为（Exj，Enj，Hej），其中，最能代表指标j和等级c这个定性概念间的转换的值是该等级区间的中间值，即Exj=（c1+c2）／2，c1和c2分别为指标j对应评估等级c的临界值。从一个等级到另一个等级的过渡值即为临界值，其应是一个模糊边界，同时属于上、下2个等级，且对2个等级的隶属度相等，故有0.5，从而。超熵Hej则可以根据Enj的大小，通过经验和重复试验获得。根据获得的云数字特征值和实际指标数据，可以获得各单一指标对每个等级的隶属度]，其中 E′n是以En为期望、He为标准差的正态随机数。

以图1“电气试验”中的“泄漏电流”为例，泄漏电流小于50 μA时变压器状态为良好，介于50～80 μA之间时状态为注意，大于80μA时可判定状态为严重，因此得到泄漏电流相对劣化度函数，其中，x为20℃ 时变压器泄漏电流的实测值。

变压器评估状态分为良好状态、一般状态、注意状态和严重状态。对于良好状态，由泄漏电流相对劣化度函数计算出模糊隶属度函数为：

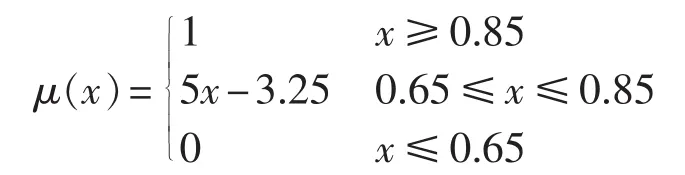
由于评语“良好”只有左单边约束，采用左半云模型描述，得到Ex、En分别为：

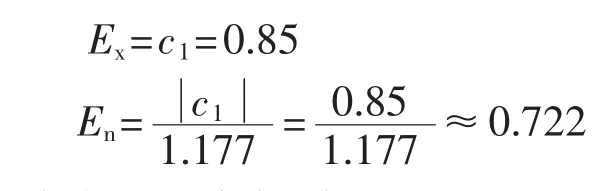
通过多次试验确定，本文中He=0.005。

同样，对于一般状态、注意状态和严重状态进行计算，从而得到泄漏电流的4个状态的模糊隶属度函数以及云模型函数如表1所示。

表1 泄漏电流的模糊隶属度函数和云模型函数Table 1 Fuzzy membership function and cloud model function of leakage current

同样，假设绝缘电阻为800 MΩ，吸收比为0.5，介损值为0.33%（32℃ 情况下），可以得到绝缘电阻对 4 个等级的隶属度为 u=[1，0，0，0]，吸收比对 4个等级的隶属度为 u=[0.277，0.589，0.134，0]，介损值对 4 个等级的隶属度为 u=[0.1282，0.7438，0.1277，0.0003]。

因此，电气试验项目层中指标对4个等级的隶属度就构成了评判矩阵：

同理，可以得到绝缘油试验和油中溶解气体的评判矩阵。

4 电力变压器状态评估步骤

其中，wvi为第i个指标的变权重；wi为第i个指标的常权重；xi为第i个指标归一化后的值；n为评估指标个数；α为均衡函数，0≤α≤1，其取值取决于各指标的相对重要程度。当排除某些指标的严重缺陷时，取α<0.5；当对指标的均衡程度要求不高时，取α>0.5；当 α=1 时，式（4）就等同于常权公式。

对于变压器状态评估指标，考虑到关键参数或设备的严重偏离正常状态将影响整个变压器安全，对电气试验和绝缘油试验中定量评估指标取α=0.1；定性评估指标用专家评分法，取α=1，作常权处理。

c.建立评价集 V=｛v1，v2，v3，v4｝，其中 v1、v2、v3、v4分别表示变压器的良好、一般、注意、严重状态等级。

d.求取变压器状态评估体系中各项目层的评判矩阵。

对于定量评估指标，计算各指标对4种状态的云模型表述，结合实际指标数据可以获得各指标对4种状态的隶属度值，从而得评判矩阵Ri。

对于定性评估指标，根据运行数据和历史数据，采用专家评分的方法确定其隶属度，从而得到评判矩阵Ri。隶属度计算公式为：

a.建立如图1所示的变压器状态评估指标体系，进行相应的状态量数据采集，获取图1涉及的与变压器状态相关的单项状态量信息。

b.采用基于合作博弈确定组合权重的方法确定各指标的常权，再由变权公式对常权进行修正，得到变权Wi。

固定权重无法反映个别关键参数严重偏离正常值时对变压器状态带来的影响，因此采用文献[17]带均衡函数的变权公式为：

e.采用的变压器状态评估体系是多层结构，需要进行分层评估，先进行项目层的评估，得到评估向量Bi=WiRi，然后将项目层评估结果组合成目标层的评判矩阵，得到目标层的评估向量B=WR。

f.根据B中的数值，采用最大隶属度法，取与最大评估值bmax=max｛bi｜i=1，2，3，4｝相对应的评判集元素vj作为评估结果，从而判断出变压器状态等级。

5 实例分析

以福建省网某台SFP7－120000／220型号变压器为例验证本文提出方法的有效性，变压器额定容量、额定电压分别为120 MV·A和220 kV。

2006年9 月初对该台变压器进行换油。换油后，于同年9月20日按照标准 DL／T596—2005[18]对变压器进行预防性试验。环境温度为14℃，环境湿度为70%，油温为33℃。2010年10月1日在相同温度、湿度和油温的情况下，按照相同标准再次对变压器进行预防性试验，其间未对变压器再进行过换油。

在2006年9月20日和2010年10月1日进行的预防性试验得到的数据如表2所示。

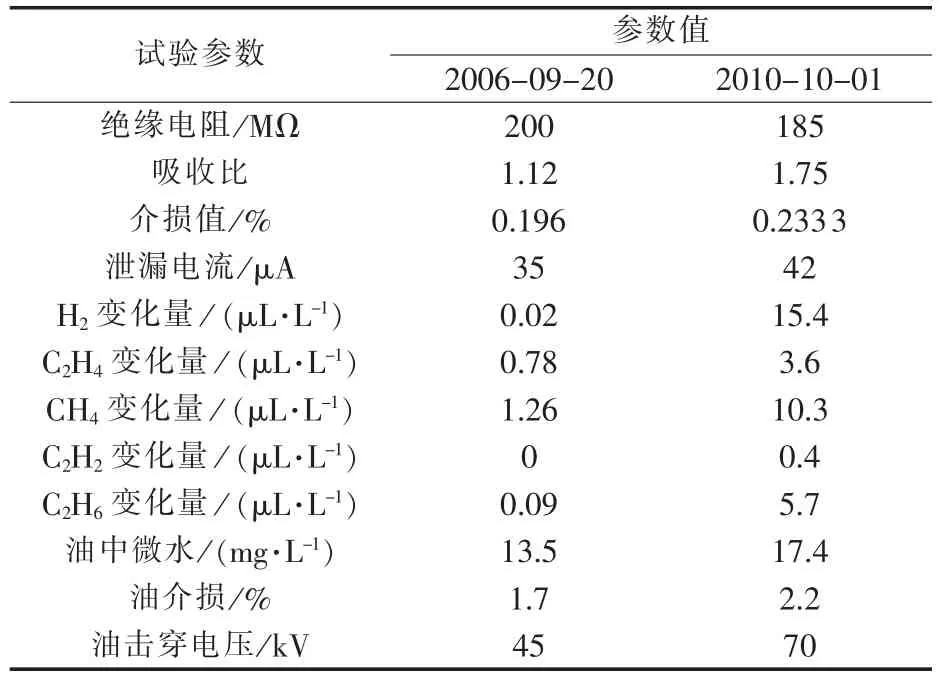
表2 变压器预防性试验数据Table 2 Data of transformer preventive test

表2中，所有实测值均已按规程换算到20℃下；气体的变化量是指气体的绝对产气速率；对测量电气试验值，取其偏差出厂值。

巡检信息：变压器的外观内外漆膜光泽度下降，有锈蚀油垢，变压器的呼吸器各连管畅通，变压器无闪络痕迹，有轻微的振动现象和过热现象。

运行工况：变压器在运行期间受到过雷击，经历过短期急救负载，运行环境温度为14℃，湿度为70%，环境因素良好，空气质量为中度污染。

附件存在的问题：冷却器、片式散热器及其油管路内部存在脏污附着与锈蚀，分接开关操作时有不正常的噪声与振动。

运行年限：该变压器1995年投运，到2010年，其运行年限为15 a。

检修记录：运行期间对变压器进行过2次维修。

a.采用合作博弈的方法计算电气试验和绝缘油试验中各指标的常权，结果如表3所示。

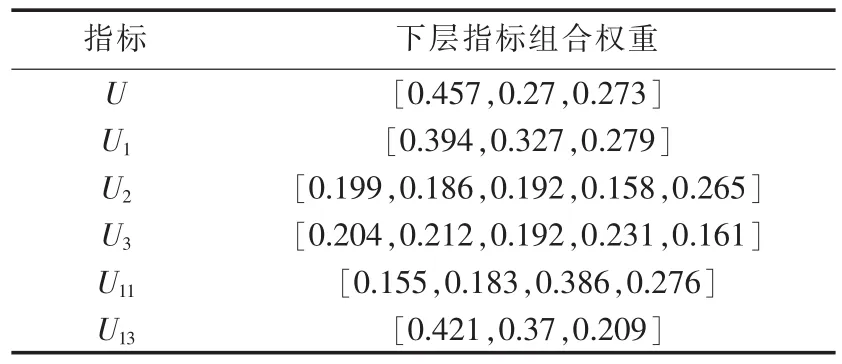
表3 采用合作博弈方法获得的组合权重Table 3 Combination weights by cooperative game method

b.根据2006年和2010年实测数据和式（4）计算电气试验和绝缘油试验中各指标的变权，见表4。

表4 电气试验和绝缘油试验中各指标的变权Table 4 Variable weights of indexes for electrical test and insulating oil test

c.计算技术指标项目层的评判矩阵。

对于油中溶解气体中的定量评估指标，由于各指标无法直接求得相对劣化度，因此采用文献[12]构建BP神经网络的方法得到指标的模糊隶属度函数。其他定量评估指标可由相对劣化度求取模糊隶属度函数。再采用云模型代替模糊隶属度函数计算出各定量评估指标的云模型表述，结果如表5所示。

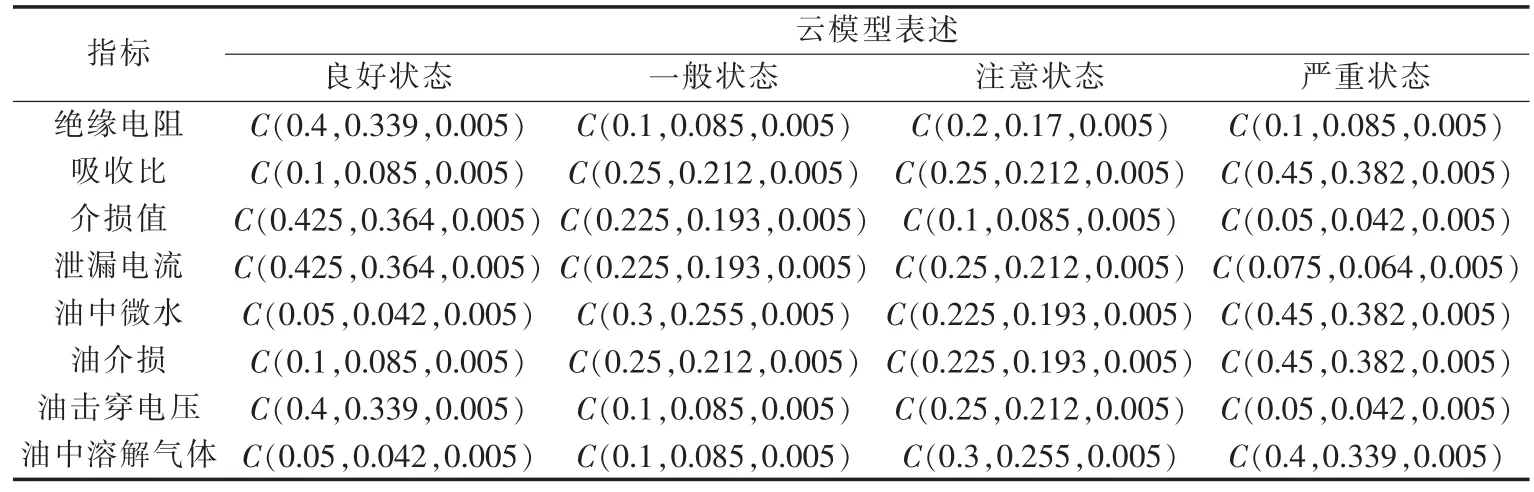
表5 定量评估指标的云模型函数Table 5 Cloud model function of quantitative evaluation indexes

结合各定量评估指标的实测值，分别计算出评判矩阵。

电气试验项目层评判矩阵为：

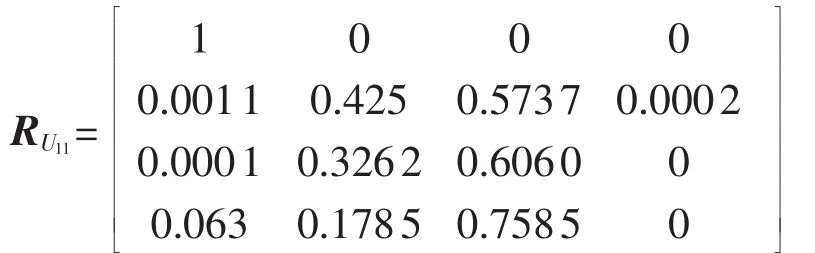
结合变权系数，求得：

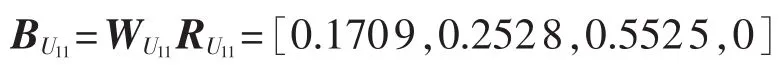
溶解气体色谱分析项目层评判矩阵为：

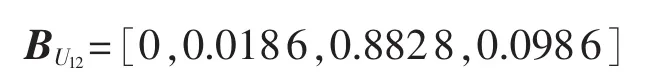
绝缘油试验项目层评判矩阵为：

结合变权系数，求得评判向量为：

因此得到技术指标项目层评判矩阵为：

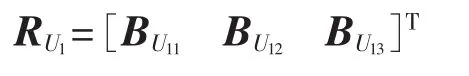
结合权重系数，可以求得评判向量为：

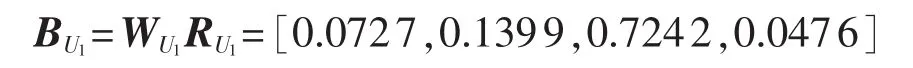
d.计算运行指标项目层和检修指标项目层的评判矩阵。

根据运行记录和历史记录采用专家评分法，由式（5）得到评判矩阵如下。

运行指标项目层评判矩阵为：

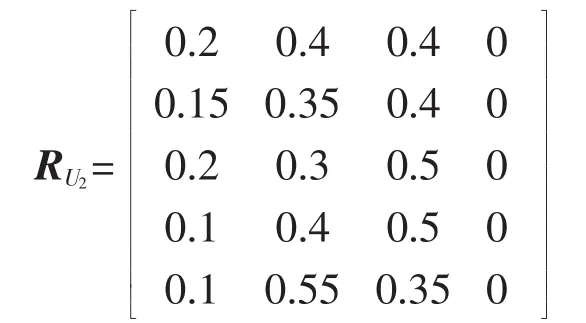
结合权重系数，可以求得评判向量为：

检修指标项目层评判矩阵为：

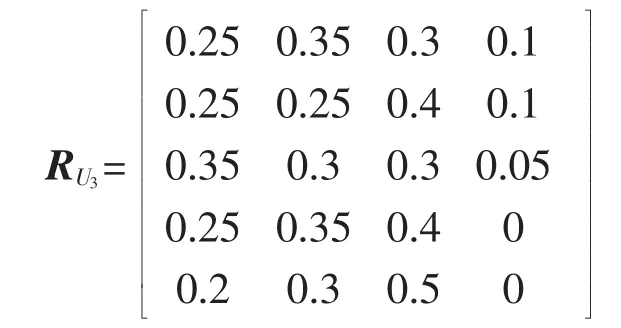
结合权重系数，可以求得评判向量为：

e.综合以上结果，求得目标层的评判矩阵为：

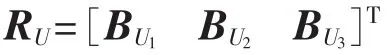
结合权重分配，可求得最终评判向量为：

利用最大隶属度法可得，变压器处于注意状态，可以认为变压器整体可靠性在下降，试验与检测到的状态量有劣化，变压器有发生故障的可能性，应该优先安排维修，并且运行中应实时监测变压器。

实际运行情况为：对变压器进行停电检修，发现由于变压器油运行时间长，分解出水分，使变压器绝缘受潮。从实际情况可知，变压器继续运行可能会发生故障，需要跟踪观察，并且优先安排维修。所以，实例表明了本文方法的有效性。

利用文献[10]的方法进行变压器状态评估，得到的评判结果为 BU=[0.1556，0.4106，0.4388，0]，也可以判断出变压器处于注意状态，但一般与注意2个状态的隶属度值分别为0.4106和0.4388，数值很接近，推断变压器状态处于一般和注意之间，可以认为虽然变压器整体性能开始下降，内部存在少许裂化现象，但是仍处于比较稳定的状态，不需要优先安排维修。而实际运行情况为：变压器继续运行可能会发生故障，需要跟踪观察，并且优先安排维修。所以与文献[10]方法相比，本文的变压器状态评估方法更加符合实际情况。