基于网络拓扑结构的股票相关性研究

汪亚楠 朱家明

【摘要】针对股票的相关性，运用回归拟合、时间序列分析、复杂网络等方法，分别建立缺失值填补、股票间相关性度量、网络拓扑结构、股市板块划分等模型，首先根据缺失值填补模型对股票的周开盘价和周收盘价进行预测，把缺少的个股回报率数据补齐；然后使用Matlab、Ucinet等软件，度量出股票间相关系数矩阵，通过设定不同阈值，作出网络拓扑图，结合中心节点度最大化和股票网络平均路径最小化两个原则选取最优的股票网络，最后根据股票网络进行股市板块划分。

【关键词】股票相关性 网络拓扑结构 股市板块 Matlab Netdraw

中图分类号：F830.91 文献标识码：A

股票市场瞬息万变，使得普通的投资者对市场的掌控能力下降，从而增大了投资的风险。股票间的相关性对于风险管理、投资决策具有重要影响。己有研究表明，股票间相关程度远超出了经济基木面因素的影响。股票市场作为复杂系统日益受到人们的关注，近年来，经济、数学、社会等领域的学者都开始用复杂网络及其相关概念来研究股票市场，进而研究股票间相关性。因此，通过对股票市场的相关性进行研究，从而准确的描述不同股票之间的相关结构，特别是两只股票之间的尾部相关结构就显得尤为重要。而对于对普通的投资者来说，了解股票之间的相关关系，使用投资模型并结合自身的需求来对金融资产进行适当的组合投资，就可以达到分散风险、提高收益的目的，从而使投资行为更加理性化（安徽财经大学2014年数学建模第四次模拟）。

一、股票缺失值填补

（一）研究思路

为弥补缺失值，首先对附件所给数据进行筛选分析，可得只有指标考虑现金红利再投资的周个股回报率（W1）和不考虑现金红利再投资的周个股回报率（W2）含有缺失数据。针对W1，根据计算公式进行计算可求出该组缺失数据的值。对于不能根据此方法计算的缺失数据，对其相邻数据进行归纳，估计出该缺失数据的值。然后使用函数拟合W1、W2之间的关系，根据拟合得函数关系式，计算出W2的缺失数据。

（二）研究方法

1.填补表中W1缺失值。通过查找资料得考虑现金红利再投资的周个股回报率计算公式为：

上下周数据完整（即时间序列完整）时：

，pt表示t周的收盘价。

上下周数据不完整（即时间序列完整）时：

根据统计学不等距分组中开区间的组距用相邻组距近似代替得：

运用公式代入已知数据即可补全W1中缺失数据。

2.填补表中W2的缺失数据。首先通过对数据（W1，W2）进行相关性分析，利用这些数据来求取近似函数W2=F（W1）。式中W1为输出量，W2为被测量。

利用Excel求得W1与W2的相关系数为0.999985，相关系数接近于1，即W1与W2具有强烈的线性关系，故可以利用线性函数描述W1与W2之间的关系，由此利用此函数关系求出W2。利用Matlab拟合出W1与W2之间的函数关系式为：W2=F（W1）=0.9989 W1，该函数拟合优度极高，其模型显著，顾客通过该函数对缺失值进行预测。根据函数，运用Excel计算补全W2中缺失数值。

二、股票间相关性度量指标

（一）研究思路

为找出度量股票间相关性的合适指标，首先通过Excel分析数据，确立时间序列；再根据需要剔除时间序列不完整相关数据，并通过随机抽样选取样本数据；其次建立层次分析模型，选取股票的相关指标求股票的综合指标来研究个股股票的特点；然后根据每股综合指标研究股票间的相关性。

（二）数据处理

1.数据的筛选与处理。分析附件中数据，可得每股股票的时间维度大都为2012年1月1日至2013年8月31日，交易周为2012年第一周到2013年36周，因为在前期算收益率中剔除了交易周为2012年第一周的数据，故取2012-2周到2013-36周为时间序列。

因为附件表中由于停盘等原因出现交易周数间断的数据，首先运用Excel将这些数据剔除，其次因为2011年53周数据未知，故无法与2012年1周的数据对比计算收益率，为减少误差将2012年第一周的数据剔除。

首先通过百度百科，根据代码对股票分类：代码以300打头的创业板、代码以600、601打头的沪市A股、代码以900打头的沪市B股、代码以000打头的深市A股、代码以200打头的深圳B股、代码以002打头的中小板。然后根据分类，用Excel进行随机分层抽样47个股票样本进行分析。

（三）度量指标的确定

影响股票的主要的指标有每股票净资产，每股收益，每股现金流等，通过主成分分析，最终选取个股周收益率、个股股价、个股流通市值为评价股票的指标来分析股票间的相关性。

1.指标的量化。收益率，为了能更好的描述数据的统计性质，在这里我们选择几何收益率。通过查找相关资料得个股周收益率的计算公式为：

其中Ri（t）表示第i股股票t周收益率，取周收盘价的对数进行计算，再运用Excel按公式计算出样本数据的周收益率。

股价，个股股价指股票的交易价格，与股票的价值是相对的概念。股票价格的真实含义是企业资产的价值。本文中选取其对数进行分析，通过查找相关资料得个股周收益率的计算公式为：

个股股价=周交易金额/周交易股数

周个股流通市值，即在每周可交易的流通股股数乘以当时股价得出的流通股票总价值。

2.股票综合度量指标——层次分析模型。设股票综合度量指标为Z，收益率为Rt，股价为St，周个股流通市值为Ut，则通过层次分析得到各股票综合指标表达式为：Z=ω1Rt+ω2St+ω3Ut，其中ωi表示各變量对综合指标影响的权重。

构造结构模型

图1 层次分析结构图

两两判别矩阵

计算可得CI=2.2204×10-14，则CR=3.8284×10-16<0.1，则判断矩阵通过一致性检验，则得权重分别为：收益率0.6、股价0.3、流通股市0.1。即综合指标函数为：Zi=0.6Ri（t）+0.3Si（t）+0.1Ui（t）。Zi即为股票间的相关性的度量指标。

因此，首先可按上述公式求出每个股票不同时期的综合指数，再利用按时间序列分析个股股票时序图或建立函数，分析其变化规律。然后根据每股股票的综合指数向量Zi求出向量间的相关系数，总结出股票间的相关性。当两只股票相关性很强，可由一支股票的涨跌情况来粗略判断另一支股票的变化规律。

三、股票网络拓扑结构

（一）研究思路

根据相关性度量指标，求出相关系数矩阵，分析股票间相关性，再设置合适的阈值，通过Ucinet绘出复杂网络拓扑图，通过统计节点度，定量分析抽取的47支股票的影响力。

其中，节点i的度ki表示与该节点连接的其他节点的数目。节点的度的越大说明这个节点在某种意义上越“重要”，即这个节点所代表的股票的影响力越大。因此，通过统计出每支股票度的大小，可以分析出这只股票的重要性

（二）研究方法

利用问题二的结论，根据收益率、股价和流通市值各自的权重，计算得到的股票的综合指标Zi，于是股票i和股票j的综合指标相关系数Cij。

以抽取的样本股票为节点集，当相关系数大于或等于指定的阈值θ时就认为股票i和股票j之间有边连接，并假设链接节点的边是双向的，否则认为股票综合指标之间没有相关性，断开连接。

（三）研究结果

1.相关性分析。通过Matlab计算股票间相关系数矩阵。本股票节点对的相关系数的绝对值越大，就表示股票节点对之间的关联性越大。出现负值指股票节点对之间呈负相关，即一支股票的综合指标的涨跌情况会引起另外一支股票朝着相反方向变化，反之相反。

2.网络结构拓扑图。当指定阈值θ=0.55时，中心节点度最大化和股票网络平均路径最小，此时股票网络最优，通过Ucinet软件绘出样本股票的网络拓扑结构图，如图2：

其中节点代表股票，节点之间的连边代表股票价格波动（或其他反映股票关联的度量）之间的相关性，两股票间的相关系数大于0.55时，两节点之间就会存在连线，连线越多代表股票与其他股票间的相关性强，当该股票的变动时会影响很多股票的变动。

图2 样本股票的网络拓扑结构图

（四）结果分析——股票影响力分析

统计得每只样本股票的度为图3所示

图3 样本股票度的统计结果

由图3知第6，14，20，36，44，45支股票的度比较大，因此这六支股票影响力大，即对整个样本股票集“重要”，它们变动时会影响多支股票的涨跌变化。而第10，11，13，15，17，18，23，26，30，38，40支股票的度为0，则这九支股票的影響力小，即对整个样本股票集相对“不重要”，与其他股票间的相关性较弱。而剩余的32支股票对整个样本股票集“重要性”适中。

四、股市的板块划分

（一）研究思路

针对问题三所德的股票网络，可对股票进行板块划分并对投资者提出建议。首先设置阈值为0.55，画出的股票间网络关联图，利用UCINET进行可视化分析，从可视化分析图中我们可以看到各个股票的相对影响力，然后利用复杂网络的凝聚子群分析画出股票不同纬度的分析图。结合图表，即可整合划分出股票的不同板块。

（二）研究方法

利用Ucinet的Net-Draw程序，在股票间联系网络的可视化结构图的基础上做中心性的可视化分析，结果如图4：

图4 中心性的可视化分析图

将其进行凝聚子群分析得图5：

图5 股票网络凝聚子群图

（三）结果分析

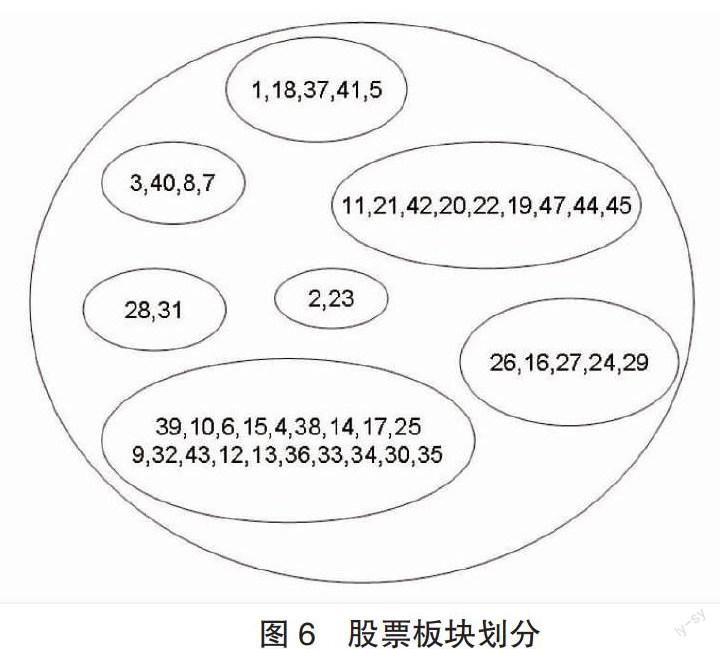
根据以上分析结果，样本股票大致可分为7个板块，划分结果如图6：

图6 股票板块划分

投资者在投资时，应关注所投资股票所属板块，并对同一板块中的其他股票行情进行研究。根据股票间相关性，参考同一板块中其他股票的行情进行投资，若同一板块中的其他股票走势低迷，即使该股行情良好，也不能轻易投资；若同一板块中的其他股票走势稳定，则可根据实情进行投资。

参考文献

[1]高惠璇.应用多元统计分析[M].北京：北京大学出版社，2005.

[2]朱广萍.应用统计学中样本容量的确定方法[J].宁夏大学学报， 2002.2，23-24.

[3]贾鹏.基于Copula方法的中国股票市场相关性研究[D].湖南大学，2012.5.

[4]刘雅倩，朱家明，王昌海.基于DCC-MGARCH模型的股票网络构建[J].嘉兴学院学报，2015.3.

[5]李柏年，吴礼斌.Matlab数据分析法[M]，北京：机械工业出版社，2012.1.

[6]杨来军，杨治辉，路飞飞.基于复杂网络理论的股票指标关联性实证分析[J].中国管理科学，2014.12.

基金项目：国家自然科学基金（编号：11301001）；安徽财经大学教研项目（acjyzd201429）；安徽财经大学科研项目（XSKY1563）

作者简介：汪亚楠（1993-）女，安徽安庆人，安徽财经大学统计与应用数学学院，研究方向：统计学；朱家明（1973-），男，安徽泗县人，副教授，硕士，安徽财经大学数学建模实验室主任，研究方向：应用数学与数学建模。