虚拟手术训练系统中软组织切割模型的研究进展

程强强 刘小平 徐少平

1(南昌大学信息工程学院，南昌 330031)2(加拿大卡尔顿大学系统与计算机工程系，Ottawa K1S 5B6, 加拿大)3(南昌航空大学测试与光电工程学院，南昌 330063)

虚拟手术训练系统中软组织切割模型的研究进展

程强强1,3刘小平1,2徐少平1*

1(南昌大学信息工程学院，南昌 330031)2(加拿大卡尔顿大学系统与计算机工程系，Ottawa K1S 5B6, 加拿大)3(南昌航空大学测试与光电工程学院，南昌 330063)

虚拟手术仿真训练系统(VSSTS)较好地解决了传统临床医生培训方法中存在的培训周期长、成本高和训练对象匮乏等方面的问题，是一种经济有效的替代训练方式。人体软组织切割作为各类实际手术中最为常见和核心的手术操作类型，对其进行逼真的模拟一直是虚拟手术仿真系统研究中的难点和热点问题。在简要介绍软组织切割模型发展历程后，分别从基于网格和无网格两大建模体系对目前已提出的多种软组织切割模型进行介绍，分析并总结各种建模方法的优缺点及其在各类虚拟手术仿真系统中的具体应用实例。除此之外，针对近年来新提出的混合模型进行分析，并从仿真效果与计算速度角度对未来的发展方向进行展望。

虚拟手术； 软组织； 切割模型； 无网格； 混合模型

引言

传统的医生训练模式周期长、效率低、成本高[1]，而且在培训过程中医生主刀的机会很少，真正进行实际手术时很容易导致医疗事故的发生。基于虚拟现实技术构建的虚拟手术仿真训练系统(virtual surgery simulation training system，VSSTS)可模拟手术中各种复杂情景，具有成本低、效率高、无损反复使用等特点，在医疗教学中正逐步占据主要地位。软组织切割作为手术中最常见、使用频率最高的操作，对其进行“无失真”模拟具有重要的意义，是虚拟手术仿真中最为核心的研究内容。然而，软组织是一种极为特殊的复合弹性材料，具有各向异性、非均匀黏弹性、近似不可压缩性。如何在虚拟手术仿真系统中建立准确、逼真的软组织切割模型一直是该领域的热点和难题[2]，主要体现在：软组织在切割后，由于几何和拓扑结构发生了剧烈的变化，特别是在有网格方法中需要重新建立网格关系，将给模型的建立带来很大的问题[3-5]；模型执行速度与仿真精度之间存在矛盾；此外，快速有效的实时碰撞检测技术对于模型也非常关键[6]。

经过近10年的发展，研究者已经提出许多软组织切割模型[2]。按照在建模过程中是否需要对虚拟器官对象进行剖分预处理，软组织切割模型可以简单分为基于网格的和基于无网格的两大建模体系架构。一是基于网格的模型，二是基于无网格的模型。

1997年，Nielsen等提出的基于网格的单元去除法[7]是最早的切割模拟方法。为改善切口仿真效果，Nielsen及其他学者相继提出了边折叠法[8]、顶点分裂法[9]、顶点复制拆分法[10]、表面约束法[11]、切口独立绘制[12]等改进模型。上述切割模型其实仅仅对虚拟对象的表面网格进行了处理，用较少的点和面片元素表示出物体的表面轮廓，计算时间短、效率高。但是，该模型无法表达出物体的内部信息，发生形变时无法真实模拟实体的各项物理性能。为了更好地模拟和表现物体被切割后内部发生的各种变化，Bielser等提出了基于体模型的体元剖分法[13]。为了解决基于体模型方法中计算速度和仿真精度的矛盾，相继出现了虚拟节点法[14-16]、部分剖分法[17]、状态机法[18]、最小分裂单元法[19]、立方体体元剖分法[20-24]等改进模型。扩展有限元方法(extended finite element method，XFEM)是目前基于网格方法中一个新的研究热点，该方法将不连续场与网格边界分开描述[25-29]，计算网格和结构内部的几何或者物理界面相互独立，特别适合分析像切割这样会造成不连续的问题。上述这些模型均需进行网格剖分预处理，在切割过程中对网格进行更新、重组，计算代价非常高。

1995年，Desbrun等将无网格方法引入计算机图形学[30]。2004年，瑞士苏黎世联邦理工学院(ETH)的Muller等提出了基于位移矢量场梯度的无网格方法来模拟弹性、塑性、融溶性物体[31]。随后，Mark等在该算法的基础上，利用透明性准则处理由切割、断裂产生的不连续性，实现了对脆性固体、高塑性软体切割、断裂的动画模拟[32]。这些无网格方法都是基于点图元的，离散和计算过程中都没有形函数的参与，不是真正意义上的无网格方法。2010年，Horton等首次提出了基于全局拉格朗日自适应动态松弛的无网格(meshless total Lagrangian adaptive dynamic relaxation, MTLADR)方法[33]。2012年，Jin等在此基础上利用水平集(level set)方法提出了基于MTLADR的切割算法[34]，实现了对2D物体的切割模拟。2013年，该研究小组成功将该算法扩展到3D物体上[35]。

下面将按照基于网格的和基于无网格的两大建模体系架构，对当前已公开发表的各种模型进行介绍，并对比总结各种方法的优缺点。随后，从仿真效果与计算速度角度，对新出现的基于网格和无网格的混合模型进行重点阐述。最后，对软组织切割模型建模方法进行总结，并对未来发展方向进行展望。

1 基于网格的切割模型

1.1 基于表面网格的切割模型

基于表面网格的切割模型相对比较简单，大致可分为3类：单元去除法、顶点复制拆分法、表面约束法。

单元去除法的基本思想是直接删除碰撞检测到与手术器械相交的单元网格形成切割缺口。这类方法最大的优点是数据计算处理速度快，编程实现简单，可实现实时处理；缺点是删除数据后模型不再满足基本的质量守恒定律，会形成锯齿状边界，仿真效果不佳。

顶点分裂方法是在几何上对切割路径上顶点运动的方向和速度进行分析，将每个顶点分裂为对称的两个新顶点[36]。这类方法适合处理几何结构规则、简单的对象，切割后可以保证其他网格的拓扑结构完整不受影响，数据结构也相对简单。

表面约束法是2010年由日本学者Megumi提出的，这类方法通过对切割路径上的顶点、添加不同的约束条件来模拟仿真切割的过程。

不论哪种基于表面网格的软组织切割模型，都只能模拟物体发生切割后组织表面发生的变化，无法表达出组织内部的各种形态，特别是在需要进行交互时，由于内部未建立模型，组织被切开后手术刀若再深入便没有意义，只能继续沿着表面进行切割，这与实际的切割相去甚远，不能模拟出真正手术时的切割“手感”。

1.2 基于体元的切割模型

根据对重构组织内部剖分时所采用的体元类型，基于体元的切割模型，可以分为基于四面体、六面体、多面体体元等的类型。

1.2.1 基于四面体体元的切割模型

最早Cotin等将单元去除方法运用于模拟肝脏切除的手术中，实现了肝脏的虚拟实时切割[37]。为了改进直接去除法的切口效果，Forset等考虑了切割位置周围四面体的影响并做了适当移除，以使模型具有一定的流体特征，但是效果仍然不够理想[38]。随后，Bielser提出体元剖分重组法，这是相对比较成熟、完备的基于网格的切割算法。该算法的基本思路是：将手术刀面与虚拟软组织四面体体元的点、边、面的交互情况分为五大类拓扑结构，其中两类是将体元部分切割，其余3类为完全切开。根据切割时的位置不同，通过顶点复制，网格重组后这5类结构的四面体体元又可细分为17个小的四面体体元，预先将这5种拓扑结构映射到17种体元细分类型中制成链表，切割模拟时直接查表即可。该方法最大的缺陷在于数据量大，数据机构复杂。同时，在对体元进行剖分、重组的过程中，会产生许多狭长、扁平的四面体体元。在运用有限元方法进行数值求解的过程中，容易产生病态矩阵，导致整个系统稳定性差，甚至无法求解。针对数据量大的问题，研究人员提出了基于最少单元创建的方法[39-40]，尽可能减少剖分出新的四面体体元。而对于容易产生病态体元的问题，Molino等提出了虚拟节点的概念。该算法的基本思想是：复制发生了切割的节点，并将原来组成物体的节点(真实节点)与新复制产生的节点(虚拟节点)进行统一，这样切割形变的计算就在良好的网格结构下进行，避免了病态体元。在最初的虚拟顶点算法中，要求必须有一个真实节点。2007年，Sifakis等对该算法进行了改进，可对纯粹的虚拟节点进行复制，这样就允许对任意四面体体元进行切割，但没有提及如何更新切割后每个单元体的质量及如何加载切割力。2010年，针对体元剖分数据量大、无法实现实时的问题，法国的INRIA小组将切割过程分为3个步骤[41]。首先，移除当前网格中与手术器械相交的体元；然后，对移除的体元进行剖分；最后，将剖分后的单元添加到原位置。其中，剖分过程会影响系统的刚度、质量、阻尼矩阵及最后的线性系统控制矩阵，在对这些量进行更新时产生了延迟，而延迟会导致系统不稳定和不准确。为了消除延迟，该小组又提出了一种在低频率下基于异步更新的预处理技术[42]。通过异步预处理器，在下一步更新前，预先将切割影响的各个矩阵计算好并存储，以便在切割过程中直接调用，尽量减少延迟，从而消除因为延迟所带来的各种不利影响。该组研究人员结合GPU并行运算技术，将该算法运用于白内障切除、腹腔内窥镜肝切除、脑瘤移除3个极具挑战的手术模拟中，取得了不错的效果，图1为模拟脑瘤切除手术。

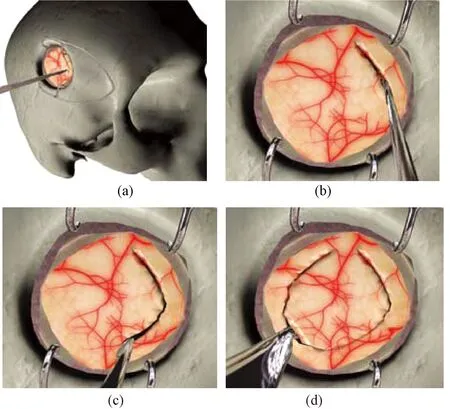
图1 脑瘤切除手术模拟[42]。 (a)开颅;(b)开始切割;(c)切割行进中;(d)切割完成Fig.1 Simulation of brain tumor resection[42].(a) Craniotomy; (b) Beginning of cutting; (c) The process of cutting; (d) Completing cutting

1.2.2 基于六面体体元的切割模型

2009年，意大利的Pietroni运用体素化技术建立了基于六面体体元的软组织模型，并提出基于此模型的分裂立方体切割算法。该算法的主要思想是：用一个规则的立方体网格包围可变形的软组织模型，然后根据建立的虚拟物体模型表面和切口边界与立方体网格相交的不同情况建立查询表，切割发生时快速查表做出相应响应。这种方法的优点在于不用担心会产生病态体元，不会因为错误而导致终止，具有良好的鲁棒性，切割响应速度很快，因为响应表是预先处理好的。由于仅仅是对分裂后的规则立方体网格边进行处理，不会出现网格法中的病态网格。与顶点拆分和复制方法不同，该方法可以实现对边、体单元的分割，德国慕尼黑工业大学的Dick 等在该领域做了许多工作。在实际模拟中，固定的网格结构不仅需要很多的内存空间，而且处理时间过长。对此，2011年Dick等提出了基于自适应八叉树网格结构的切割方法。该方法根据切割轨迹，自适应地将网格结构调整至某个最佳水平。在这种情况下，体元之间的关联仍然与在固定网格中的一致。但是，实际上仅仅需要保存在最佳水平下的体元。这样，可以大大减少内存的存储空间，同时提高处理速度。对于切割表面的渲染，Wu 等提出了双等值线法(dual contouring)。相对于前面提到的立方体分裂法，该方法不但可以提高所生成的网格质量，同时可以减少三角形的总数量。如图2所示，将该方法应用于由17万个体元组成的肝脏模型切割试验中,图像刷新率可达到15帧/s，基本满足实时性要求。

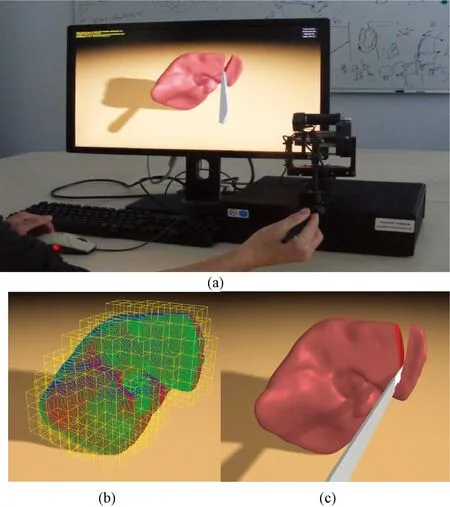
图2 基于六面体体元的切割算法试验效果图[22]。(a)装置; (b)网格化; (c)切割渲染Fig.2 Cutting based on hexahedron vexel[22]. (a) Equipment; (b) Meshing; (c) Cutting rendering

1.2.3 基于多面体体元的切割模型

对基于四面体或者六面体体元的软组织模型而言，切割后进行网格重组的体元仍然必须为四面体或者六面体。为了打破这种限制，Wicke等提出了基于多面体体元的切割模型[43]。在该模型下，允许切割后产生的体元为其他类型，虽然这类方法给网格重组带来了很大的方便，但是在重组过程中仍然很容易产生病态体元，造成系统不稳定，所以需要进一步研究改进。

1.3 扩展的有限元方法

软组织被切割后必然会产生新的边界，造成不连续性。传统的有限元方法采用连续函数作为形函数，要求在单元内部形函数连续且材料性能不能跳跃，因而对于像切割这样会产生移动边界的手术操作很难分析。基于此，研究者提出了XFEM，该方法最早是由美国西北大学一直从事计算力学研究的著名学者Belytschko提出，主要用于金属等刚性物质裂纹扩展的模拟仿真，后来应用到2D和3D弹塑性物体形变、流体力学等领域。2004年，Vigneron等将XFEM方法运用于外科手术的切割模拟中，利用具有不连续性质的扩展形函数来表示间断，将不连续场与网格边界分开描述。2009年Luis等提出了一种用于软组织切割的XFEM框架，运用一种FEM-XFEM的映射方法，当体元进行分裂时插入一个备选的网格(alternative tetrahedral mesh, ATM)。由于这种映射方法储存了顶点和体元的关系结构，切割进行时可以快速地建立起点和体元的联系，如图3所示。在人脸和人手上的试验结果表明，该算法计算速度快、稳定，可满足实时性要求。最近，德国Heidelberg 大学的Nicolai 等将共旋坐标法(corotational formulation)和隐式Newmark积分方法引入到X-FEM的框架中，前者在实时模拟时可以对复杂的形函数梯度的计算进行预处理，后者可以增强仿真过程的稳定性。图4所示为应用该方法对虚拟肝脏任意切割的模拟结果。

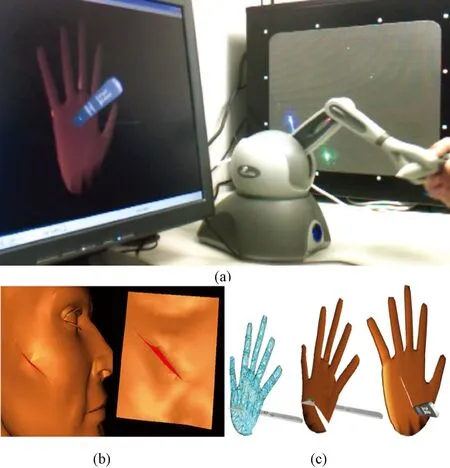
图3 X-FEM切割算法2D切割试验效果[28]。(a)装置;(b)人脸试验;(c)人手试验Fig.3 2D cutting based on X-FEM[28]. (a) Equipment; (b) Cutting on man’s face; (c) Cutting on the hand

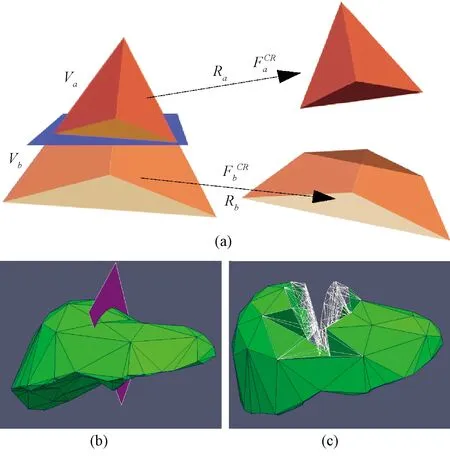
图4 X-FEM切割算法3D切割试验效果[29]。(a)四面体分裂; (b)切割开始; (c)切开后Fig.4 3D cutting based on X-FEM[29].(a) Tetrahedron splitting; (b) Beginning of cutting; (c) Results of cutting

2 基于无网格的切割模型

目前在软组织模拟仿真问题上，绝大多数基于网格的数值求解方法为有限元法(finite element method, FEM)。有限元方法需要首先对物体进行网格剖分，对于复杂物体这一过程容易形成病态网格，而且非常耗时。同时，切割过程会破坏原有的网格结构，须对原始网格进行重组，这往往是非常困难的事情。在这种背景下，基于无网格的切割模型应运而生[44]。

2.1 基于位移场矢量梯度的无网格方法

Desbrun等最早将无网格方法引入计算机图形学中，并运用于可变形物体的模拟。2004年，瑞士ETH实验室的Muller等运用移动最小二乘法(moving least squares, MLS)计算每一个节点的位移向量场梯度，在此基础上计算得到任意点的应力、应变和弹性力，从而实现了基于点的弹性、塑性、融溶性物体的模拟仿真。当在外力作用下任意点的位移发生变化后将产生位移场变量，通过求导可求出位移场对应3个坐标的位移场矢量的梯度；接着利用该梯度，可计算出应力和应变；然后根据应变能梯度的负数与位移场矢量的乘积，得到任一点所受体力；最后运用蛙跳法(leap-forg)，计算出任一点新的位移。由于组成物体的物理点元(physical elements, Phyxels)相互影响，因此仅可对物体形变进行模拟，无法模拟切割或断裂。2005年,斯坦福大学的Mark等在该算法基础上，利用透明性准则处理由切割、断裂产生的不连续性，实现了对脆性固体、高塑性软体的切割、断裂的动画模拟。与传统的FEM方法中网格始终保持一致不同，该方法动态地调整节点的形函数，同时运用插值方法不断对离散后的空间进行修正，这样使得模拟出来的切口效果非常好。但是，该方法很难权衡内存和动态重算的关系，而且不适合对薄壳类物体进行模拟。针对这些问题，2006年Guo等提出了基于全局共形参数化的薄壳无网格模拟[45]。2012年，韩国Jung等利用一种拓扑结构快速细分方法，对组成物体的无网格节点进行分裂[46]。该方法首先基于可见性准则，建立起节点间拓扑关系-无向图(undirected graph)；接着，运用层次包围盒方法(bounding volume hierarchy, BVH)，快速测试手术器械与软组织碰撞情况；然后，根据碰撞结果，删除无向图中受切割影响的边；最后，运用BVH法，对无向图不断地进行更新重构，从而实现切割的实时模拟。该算法最大亮点在于BVH算法相对其他碰撞方法(如空间散列法)效率更高，很适合运用于可形变体的自适应调整。如图5所示，Jung等在普通PC机上对由7 629个节点重构的虚拟肝脏组织上进行试验，实时切割模拟速度可达20 Hz。该方法不算真正意义上的无网格方法，因为每个节点之间还是通过无向图建立了联系，切割过程中也需不断根据碰撞检测结果对无向图进行更新。

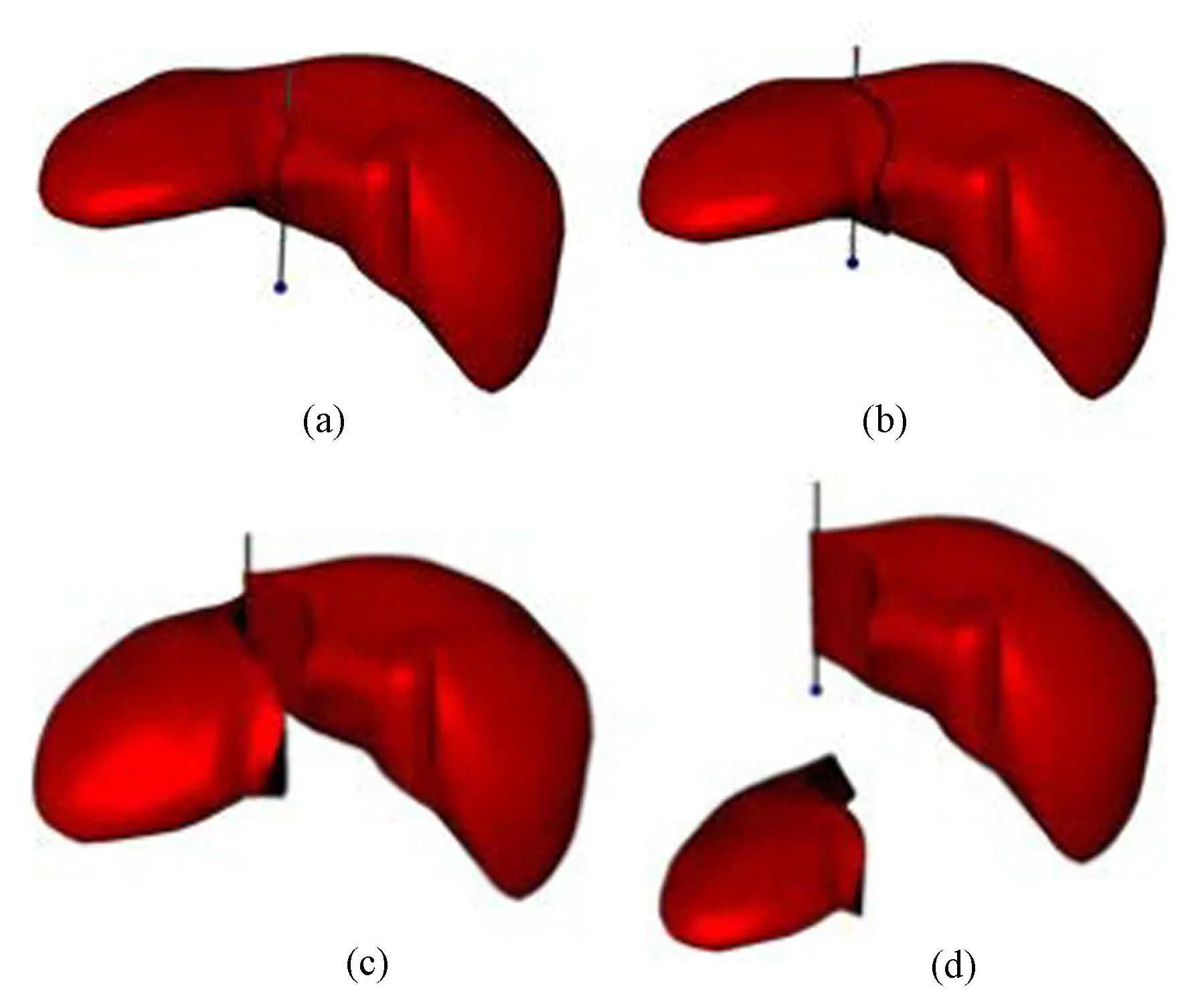
图5 基于BVH的无网格切割算法试验效果[46]。 (a)开始切割;(b)切割进行中;(c)部分切开;(d)完全切开Fig.5 Meshless cutting method based on of BVH[46]. (a)Beginning of cutting;(b)In the process of cutting;(c)Partial cutting;(d)Completing of cutting

2.2 EFG无网格方法

EFG方法是无网格方法中一种成熟并广泛使用的方法。在本文上一节的介绍中，ETH的Muller等提出基于位移场矢量梯度的无网格方法以及在此基础上发展的切割算法并不是真正意义上的无网格方法，因为这类方法中没有形函数的概念，应力、应变以及后面计算的体力都是基于位移场矢量的梯度[47]。2010年，Horton等首次提出了基于全局拉格朗日自适应动态松弛的无网格(MTLADR)方法[48]。在一个重构的圆柱体上进行了压缩、拉伸等形变试验，通过与FEM的结果对比，该算法计算出的体力和位移与FEM的误差小于5%。2012年，Jin等在此基础上提出了基于MTLADR的软组织切割算法[49]。MTLADR属于EFG方法的一种，特别适用于像切割这样会造成边界移动的情况。首先，在点云模型基础上，构建背景网格，并计算形函数及其导数；其次，运用水平集方法对点进行分类；再次，利用可见性准则调整点的形函数，将一些由于切割而造成“不可见”的点从影响域中删除，并更新形函数；然后，计算并组装体力；最后，将所求得的体力带入物体运动控制方程，并求解得到各点的新位移。为了验证基于MTLADR的切割算法的可行性与准确性，在一个重构的0.1 m×0.1 m正方形点云样本上进行了切割试验，并将该算法的计算结果与有限元软件Abaqus的计算结果进行对比，发现两者具有很好的一致性。2013年，Jin等将MTLADR算法扩展到3D软组织切割模拟，如图6所示。在2D空间中，切割路径用一系列线段进行表示；扩展到3D后，切割路径则用一系列切割平面来表示。笔者同样将MTLADR算法计算结果与Abaqus计算结果进行对比，结果表明：两者最大绝对误差为0.78 mm,平均误差为0.039 mm, 95.76%的节点绝对误差小于0.1 mm。

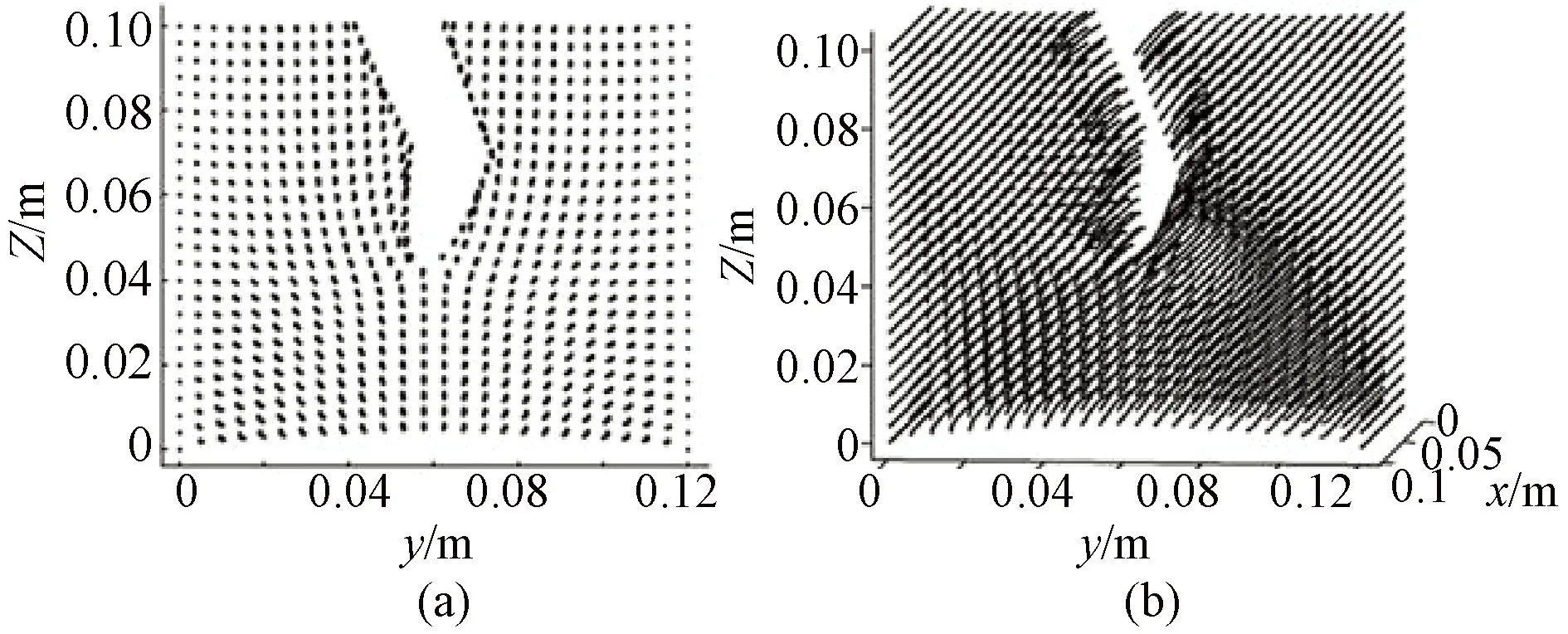
图6 基于MTLADR算法的切割试验效果[35]。(a)2D切割；(b)3D切割Fig.6 Cutting based on MTLADR[35].(a)Result of 2D cutting; (b)Result of 3D cutting

从目前公开发表的文献看，运用该算法进行模拟的对象均是具各种材料性质的弹性正方体，后期没有贴纹理或其他渲染处理，所得到的渲染结果比较生硬，无法获得令人满意的虚拟现实效果。为了将该方法真正运用于虚拟手术仿真中，笔者首先在规则正方体上进行了试验，图7中(a)和(b)是随着切割的进行切口不断张开的过程，试验结果表明了这种算法的可行性。接着，将该算法应用于脑外科虚拟手术训练仿真系统中对脑瘤组织切割模拟，并对切口进行纹理贴图和渲染，从图(c)中可以看出切割后形成的切口很平滑，取得了不错的视觉效果。目前，该算法存在的主要问题是计算速度很慢，无法满足实时性要求。产生这个问题的根源在于该算法属于EFG方法的一种，由于EFG的计算过程中需要借助背景网格进行高斯积分，导致运算量非常大，这个问题有待进一步解决。

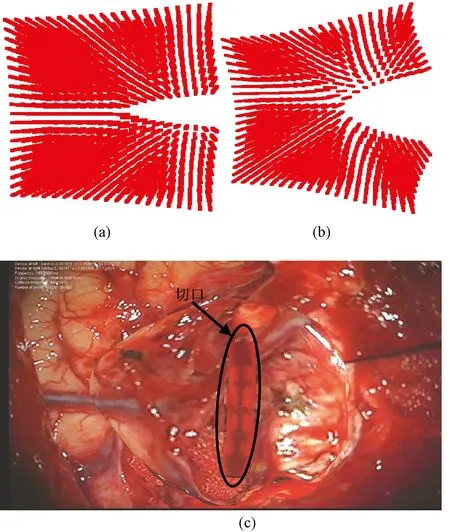
图7 虚拟脑外科手术脑瘤切割试验效果。 (a)较浅的切口；(b)较深的切口；(c)切口渲染Fig.7 Brain tumor resection for brain surgery. (a)Shallow incision;(b)Deep incision;(c)Incision rendering

3 网格法和无网格法的混合切割模型

基于网格的软组织切割模型算法相对成熟,通用性好。但是，在进行单元网格剖分等预处理时工作量大，特别是对于复杂形状的三维物体需要耗费大量的时间建立网格关系，而且往往无法建立良好的网格结构，在切割过程中为维护这种网格关系也需要耗费大量的计算代价；基于无网格的软组织切割模型使用大量无关联的节点重构物体，无需建立网格也不必描述节点之间的关系，这样就大大减少了预处理的工作量和时间，并且在切割过程中无需特别维护节点之间的拓扑关系。然而，该方法在处理边界时往往比较困难，边界条件难以施加。因此，许多学者尝试将两种方法结合起来，建立起基于网格和无网格方法的混合切割模型。

3.1 现有工作

2009年，ETH的Denis等将基于无网格的物体空间离散方法与基于网格的表面重建技术结合起来，已成功运用于子宫镜检查和切割模拟中[50]。但是，该方法数据结构复杂，算法复杂度高，计算效率低。随后，Shao等将软组织划分为手术区域和非手术区域，综合运用无网格方法中的快速格子形状匹配算法(fast lattice shape matching, FLSM)和基于网格的有限元方法，建立了可形变体虚拟切割混合模型[51]。研究人员设计了两个实时虚拟切割实例，分别用重构的虚拟手术器械对可形变的虚拟肝脏和斯坦福兔子(Stanford bunny)进行切割，如图8所示。结果表明，该方法形成的切口平滑、逼真，图像刷新率可达20帧/s，可满足实时性的要求。针对网格方法切割破坏原始的网格结构后在重组过程中产生病态网格和分裂带来的结构不一致，以及无网格方法重建切割表面复杂且低效的问题，2012年上海交通大学周喆等人提出了分别用一组表面面片表示物体轮廓和一个描述模型内部结构的点集来建立切割模型[52]。在该模型中，随着切割的进行，对切割路径上的表面网格进行分裂，而内部点集则根据无网格法中的分裂原则，将切割路径上的顶点记录并重建切割表面。这样，表面重建只需针对由于切割而产生的新表面，加快了表面重建的速度，且仅仅对切割路径上的表面网格进行分裂，内部都是由点集构成，回避了传统网格方法中网格重建时复杂的拓扑形态变化。图9给出了该算法的具体步骤，图10是在一个虚拟肝脏模型上进行的切割试验。实验结果表明，该方法可以获得沿着切割方向较为平滑的切口表面，但是由于内部插入的顶点纹理坐标无法计算，造成新形成的切割表面没有纹理。2013年，澳大利亚Curtin大学Jie等将基于表面网格的顶点复制分裂法与基于无网格的体单元传递链形变模型相结合，很好地模拟了软组织切割过程[53]。表面网格模型用于产生切割后的切口表面，在表面网格下体元形变模型则模拟切割过程中软组织的形变。为了使切割表现得更加真实，笔者采用简单的衰减函数来表达软组织因切割造成的“起皱”现象。将该算法运用于脊椎手术的模拟中，结果如图11所示。图11中的(a)～(d)是计算机模拟的效果，(e)是实际手术情况。从图11(a)～(d)中可以看出，该方法不需要插入新的节点或体单元，因此不会出现切割后切口没有纹理的问题。对比(d)和(e)可知，(d)中切割区域周围的“起皱”现象与实际手术(e)中的一致，从而增强了手术仿真的现实感。该方法存在的主要问题在于切割表面与组织内部体模型没有很好融合，切割表面如同贴在体模型上面。

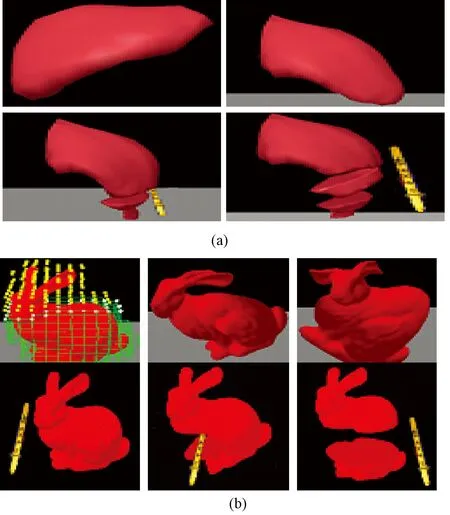
图8 基于快速格子形状匹配和有限元法混合模型[51]。 (a)肝脏模型切割；(b)兔子模型形变及切割Fig.8 Hybrid model based on FLSM and FEM[51].(a)Cutting of liver;(b)Deformation and cutting of bunny

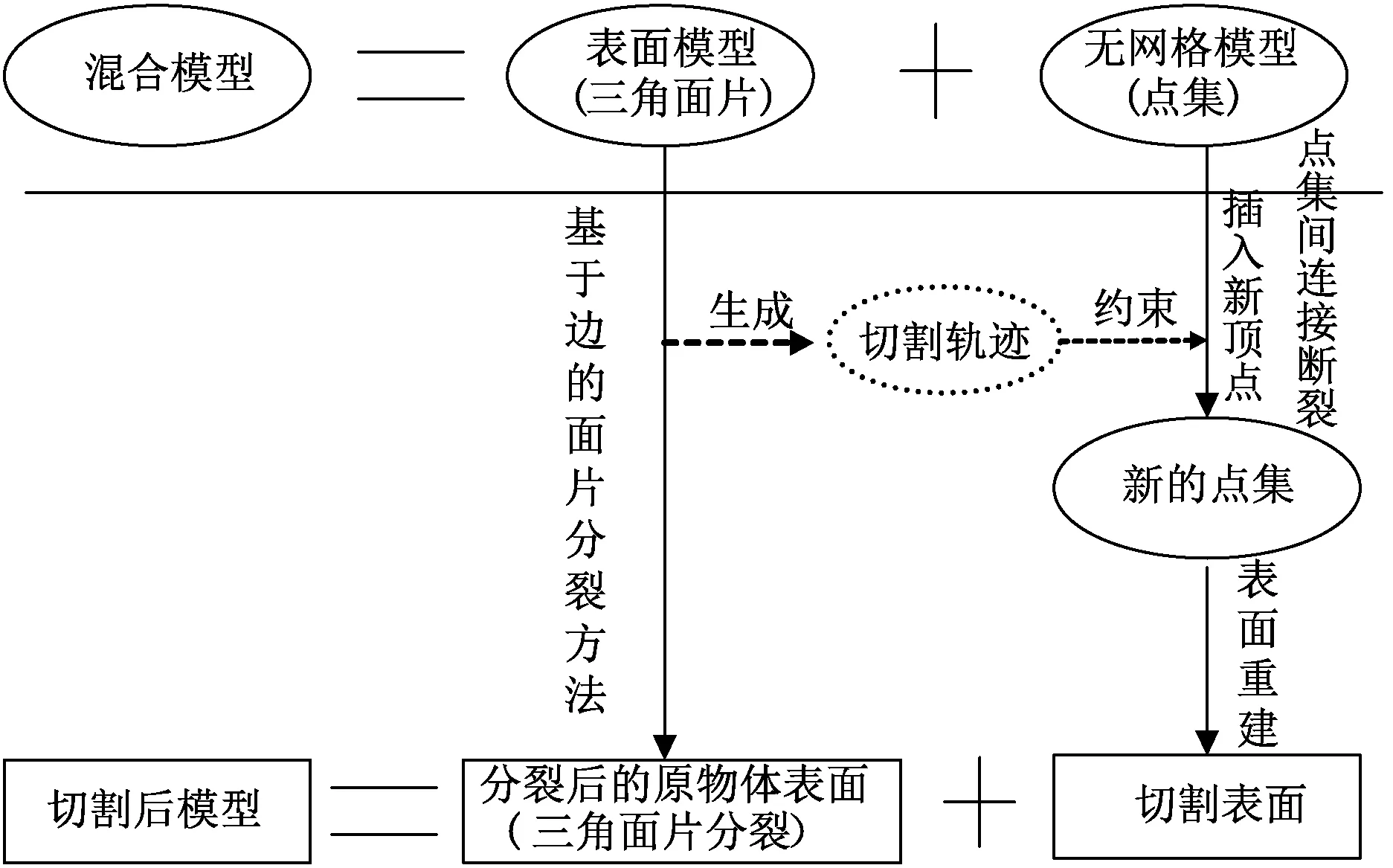
图9 基于三角面片和点集的混合模型切割算法流程[52] Fig.9 Algorithm flow of hybrid model based on triangular faces and nodes[52]

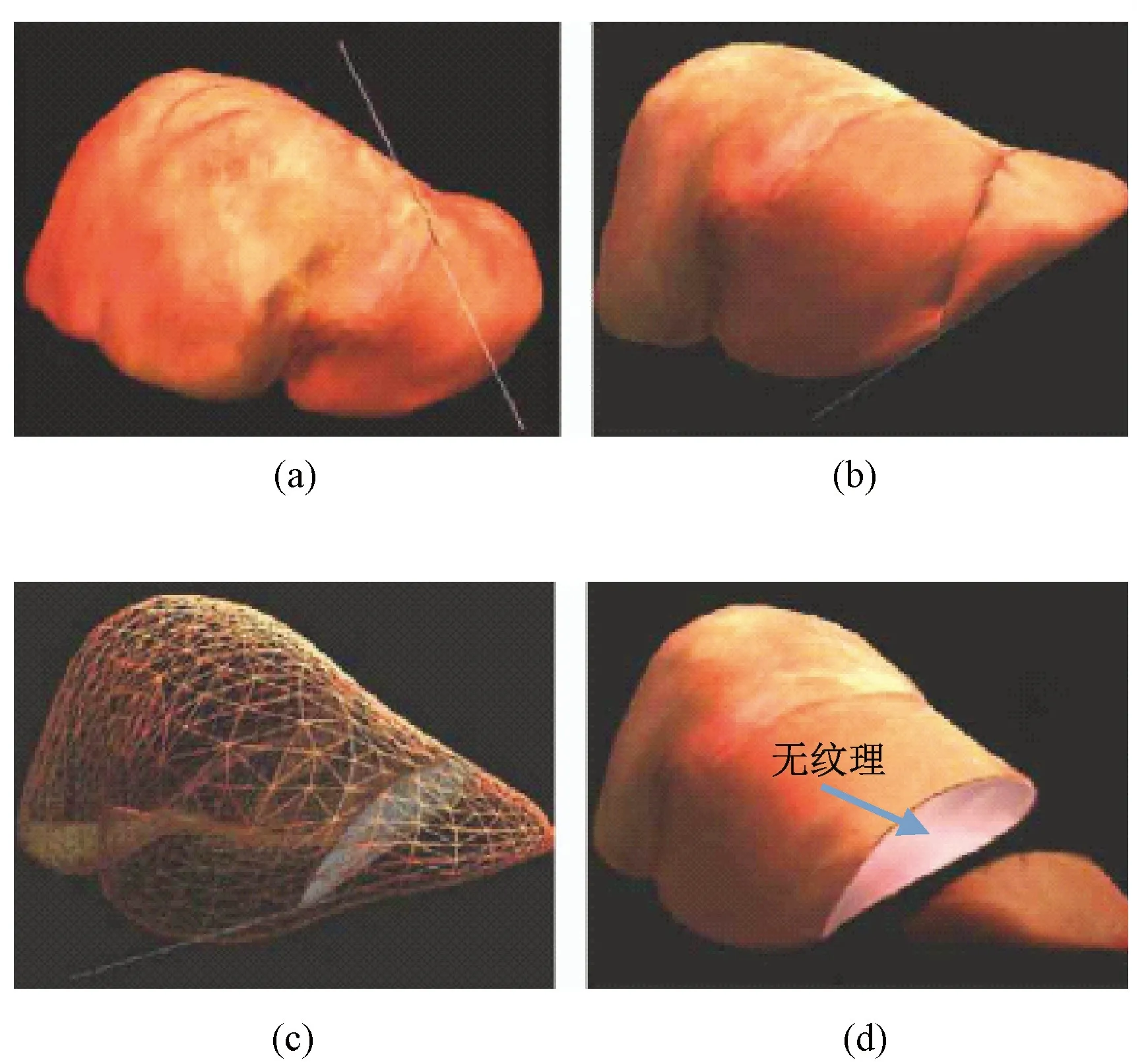
图10 基于三角面片和点集的混合模型切割试验[52]。(a)开始切割;(b)切割进行中;(c)网格结构;(d)切开后效果Fig.10 Cutting hybrid model based on triangular faces and nodes[52]. (a)Beginning of cutting; (b)In the process of cutting; (c)Mesh; (d)Results of cutting

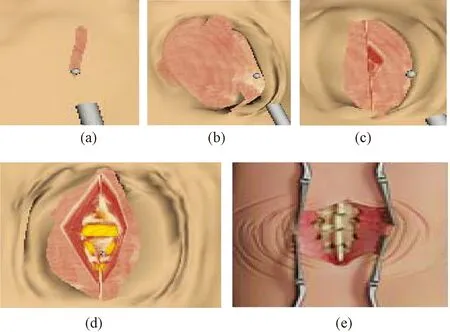
图11 基于顶点复制拆分法与体单元传递链形变模型的混合模型切割试验效果[53]. (a)～(d)模拟切割过程;(e)真实切割效果Fig.11 Cutting hybrid model based on nodes snapping and Divod Chainmail[53].(a)～(d)Simulation of the cutting process;(e)Real cutting process

3.2 优缺点分析

采用混合模型模拟切割，一般采取将软组织表面与内部分开描述的方式来进行。对于表面的建模一般都是基于有网格的方法，而对于内部体模型则采用无网格的方法。这样做的好处在于：一是基于网格的面模型数据量少，在形成切割表面及切割过程中对网格进行控制比较方便，计算速度很快；二是网格模型经过这么多年的发展有许多非常成熟的切割算法，容易得到光滑、真实的切口效果；三是无网格模型在模拟体模型形变方面具有很多优势，建模时仅仅需要保存每个节点的相关信息，数据结构简单，发生形变时只需计算单个节点的位移矢量；四是软组织在产生形变的过程中一般不容易出现如切割那样造成的新边界，仅仅是节点的位移移动，无网格方法的一个很大难点就在于本质边界条件(位移边界条件)的施加，这样就很好地避开了这个问题。

混合模型目前最大的难点是如何很好地管理好两种不同的建模体系。首先，对两种不同数据结构进行管理和维护，使两种不同的模型在切割过程中很好地协调、统一；其次，对视觉效果进行融合，因为从目前的文献看，基于网格方法产生的切割表面和基于无网格的体模型像被割裂开，还不能很好地融合在一起，无法形成统一的整体，影响视觉效果。

4 总结和展望

在虚拟手术仿真系统中，目前所建立的用于仿真软组织切割等操作的虚拟器官模型大体上都是基于网格的和基于无网格的体系架构。其中，根据是否处理内部信息，基于网格的切割模型可分为面模型和体模型两大类。面模型的优点是用较少的点和面片元素可表示出物体的表面轮廓，计算时间短、效率高。但是，该模型无法表达出物体的内部信息，发生形变时无法真实地模拟实体的物理性能；体模型采用可充满整个模型空间的体元(常用的有四面体、六面体等)，可同时表达出物体的内、外部信息,因为用三维单元来重构器官模型,仿真的物理效果较好。然而，体模型数据量大、数据结构复杂、计算时间长，运用这些基元进行模拟时，要求沿着一定的方向切割，以保持模型一致性。由于手术时切割具有随机性，因此该方法在实际应用中受到一定限制。

基于无网格的切割模拟方法，可从根本上消除基于网格方法的许多弊端，不需要维持网格结构的一致性，特别是切割后无需进行网格重组，在计算效率和算法的复杂度上具有很大的优势。基于位移矢量梯度的无网格方法，计算应力、应变都是只针对重构物体的独立点元，理论基础清晰，程序编程实现容易，非常适合对软组织形变的模拟仿真。但是，该方法没有形函数的概念，对于像切割这样会造成不连续性的模拟，位移(本质)边界条件难以施加。EFG方法通过可见性准则等处理不连续边界的手段，调整形函数,可以很好地对切割操作进行模拟。该方法最大的不足是：在进行高斯积分时需要利用背景网格，导致运算速度很慢，难以满足实时性的要求。

基于网格和无网格方法的混合模型，可以很好地发挥两个方法各自的优点，避免了各自的缺点，因此成为软组织切割建模的热点前沿课题。无论是将软组织模型按照手术区域和非手术区域划分，还是分成基于网格的表面模型和无网格的内部体模型，都需要建立两套完全不同的数据结构。在切割过程中，如何更高效地进行切换，更高效地进行组织，是未来该领域的发展方向之一。在视觉方面，由于两种模型的存在造成了面模型和体模型或者手术区域和非手术区域的割裂，不能很好地融为一体。因此，笔者认为，可以借鉴图像处理领域的边缘融合技术，实现这两者的无缝“对接”。同时，两个模型混合在一起以后，会造成数据结构复杂的问题，应该通过设计更为合理的数据结构加以解决。另外，为了达到满意的计算效率与仿真精度，采用基于GPU的各种并行计算[54-55]方法是一种选择。

[1] Xu Shaoping, Liu Xiaoping, Zhang Hua. Simulation of soft tissue using mass-spring model with simulated annealing optimization [C] //Liu Xiaoping, eds. IEEE International Conference on Automation and Logistics. Shenyang:IEEE, 2009: 1543-1547.

[2] Wu Jun, Westermann R, Dick C. Physically-based simulation of cuts in deformable bodies a survey[C] //Lefebvre S, Spagnuolo M, eds. Eurographics 2014. Strasbourg: Eurographics Association, 2014: 1-18.

[3] 徐少平，刘小平，张华，等. 虚拟手术中软组织实时形变模型的研究进展 [J].生物医学工程学杂志, 2010, 27(2): 435-439.

[4] Xu Shaoping, Liu Xiaoping, Zhang Hua,etal. A nonlinear viscoelastic tensor-mass visual model for surgery simulation [J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(1): 14-20.

[5] Liu Xiaoping, Xu Shaoping, Zhang Hua,etal. A new hybrid soft tissue model for visio-haptic simulation [J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(11): 3570-3581.

[6] Wu Jun, Dick C, Westermann R. Efficient collision detection for composite finite element simulation of cuts in deformable bodies [J]. Visual Computer, 2013, 29(6): 739-749.

[7] Bro-Nielsen M. Finite element modeling in surgery simulation [J]. Proceedings of the IEEE, 1998, 86(3): 489-503.

[8] Ganovelli F, O’Sullivan C. Animating cuts with On-The-Fly remeshing [C] //Roberts JC, eds. Eurographics 2001. Manchester: Eurographics Association, 2001: 110-113.

[9] Lim YJ, John Hu, Chang Chunyin,etal. Soft tissue deformation and cutting simulation for the multimodal surgery training [C] //Lee DJ, Nutter B, Antani S,etal, eds. Proceedings of the 19th IEEE Symposium on Computer-Based Medical Systems (CBMS’06). Salt Lake City: IEEE, 2006: 635-640.

[10] 郁松,樊晓平,廖志芳. 虚拟手术中顶点复制切割算法的设计研究[J]. 小型微型计算机系统, 2010, 31(5): 959-963.

[11] Megumi N, Kotaro M. Physics-based interactive volume manipulation for sharing surgical process [J]. IEEE Transactions on Information Technology in Biomedicine, 2010, 14(3): 809-816.

[12] 朱玲，叶秀芬，希吉尔，等.基于贝塞尔曲线的虚拟手术切割新算法 [J]. 计算机应用研究, 2013, 30(10): 3195-3200.

[13] Bielser D, Maiwald AV, Gross MH. Interactive cuts through 3-Dimensional soft tissue [J]. Computer Graphics Forum, 1999, 18(3): 31-38.

[14] Molino N, Bao Zhu, Fedkiw R. Virtual node algorithm for changing mesh topology during simulation [J]. ACM Transactions on Graphic, 2004, 23(3): 385-392.

[15] Sifakis E, Der KG, Fedkiw R. Arbitrary Cutting of Deformable Tetrahedralized Objects [C] //Metaxas D, Popovic J, eds. ACM SIGGRAPH Symposium on Computer Animation (2007). San Diego: Eurographics Association, 2007: 73-80.

[16] Sifakis E, Shinar T, Irving G,etal. Hybrid Simulation of Deformable Solids [C] //Metaxas D, Popovic J, eds. ACM SIGGRAPH Symposium on Computer Animation (2007). San Diego: Eurographics Association, 2007:81-90.

[17] Bielser D, Gross M. Interactive simulation of surgical cuts [C] //Barsky BA, Shinagawa Y, Wang Wenping, eds. Proceeding the Eighth Pacific Conference on Computer Graphics and Applications. Hong Kong: IEEE, 2000: 116-442.

[18] Bielser D, Glardon P, Teschner M,etal. A state machine for real-time cutting of tetrahedral meshes [J]. Graphical Models, 2004, 66(6): 398-417.

[19] Mor AB, Kanade T. Modifying soft tissue models: Progressive cutting with minimal new element creation [C] //Scott LD, Anthony MD, Branislav J, eds. In Proceedings of the Third International Conference on Medical Image Computing and Computer-Assisted Intervention. Pittsburgh: Springer, 2000: 598-607.

[20] Pietroni N, Ganovelli F, Cignoni P,etal. Splitting cubes: a fast and robust technique for virtual cutting [J]. The Visual Computer, 2009, 25(3): 227-239.

[21] Dick C, Georgii J, Westermann R. A hexahedral multigrid approach for simulating cuts in deformable objects [J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(11): 1663-1675.

[22] Wu Jun, Dick C, Westermann R. Interactive high-resolution boundary surfaces for deformable bodies with changing topology [C] //Bender J, Erleben K, Galin E, eds. The 8thWorkshop on Virtual Reality Interaction and Physical Simulation. Lyon: Eurographics Association, 2011:29-38.

[23] Wu Jun, Dick C, Westermann R. Efficient collision detection for composite finite element simulation of cuts in deformable bodies [J]. The Visual Computer, 2013, 29(6-8): 739-749.

[24] Wu Jun, Westermann R, Dick C. Real-time haptic cutting of high-resolution soft tissues [J]. Studies in Health Technology and Informatics, 2014, 196: 469-475.

[25] Belytschko T, Chen Hao, Xu Jingxiao,etal. Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment [J]. International Journal for Numerical Methods in Engineering, 2003, 58(12): 1873-1905.

[26] Belytschko T, Song JH, and Wang Hongwu,etal. On applications of XFEM to dynamic fracture and dislocations [C] //Combescure A, Borst RD, Belytschko T, eds. IUTAM Symposium on Discretization Methods for Evolving Discontinuities. Lyon: Springer, 2007(5): 155-170.

[27] Vigneron LM, Verly JG, Warfield SK. Modeling surgical cuts, retractions, and resections via extended finite element method [C] //Brillot C, Haynor DR, Hellier P, eds. Proceedings of Medical Image Computing & Computer Assisted Intervention. Berlin: Spring-Verlag, 2004(7): 311-318.

[28] Vigneron LM, Verly JG, Warfield SK. X-FEM framework for cutting soft tissue: including topological changes in a surgery simulation [C] //Richard P, Braz J, Hilton A, eds. International Conference on Computer Graphics Theory and Application. Angers: GRAPP, 2010: 285-302.

[29] Nicolai S, Stefan S, Rudiger D. Simulation of surgical cutting of soft tissue using the Extended Finite Element Method [EB/OL]. http://dx.doi.org/10.11588/emclpp.2013.04.11825,2013-04/2015-03

[30] Desbrun M, Cani M P. Animating soft substances with implicit surfaces [C] //Susan GM, eds. SIGGRAPH’95 Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. Los Angeles: ACM, 1995: 287-290.

[31] Müller M, Keiser R, Nealen A,etal. Point-based animation of elastic, plastic and melting objects [C] //Badler N, Desbrun M, Boulic R, Pai D, eds. Proceedings of the 2004 ACM SIGGRAPH/Eurographics symposium on Computer Animation. Los Angeles: Eurographics Association, 2004: 1-11.

[32] Pauly M, Keiser R, Adams B,etal. Meshless animation of fracturing solids [C] //Gross M, eds. ACM Transactions on Graphics(2005). Los Angeles: ACM, 2005: 957-964.

[33] Xia Jin, Grand RJ, Karol M,etal. Meshless algorithm for soft tissue cutting in surgical simulation [J]. Computer Methods in Biomedical Engineering, 2014, 17(7): 800-811.

[34] Grand RJ, Adam W, Karol M. An adaptive dynamic relaxation method for solving nonlinear finite element problems: Application to brain shift estimation [J]. International Journal for Numerical Methods in Biomedical Engineering, 2011, 27(2): 173-185.

[35] Xia Jin, Grand RJ, Karol M,etal. 3D algorithm for simulation of soft tissue cutting [M]//Models, Algorithms and Implementation. Computational Biomechanics for medicine. New York: Springer, 2013: 49-62.

[36] Seokyeol K, Jihwan P, Jinah P. Progressive mesh cutting for real-time haptic incision simulator [C] //Cani MP, Sheffer A, eds. International Conference on Computer Graphics and Interactive Techniques(2010). Seoul: ACM, 2010: 61-70.

[37] Delingette H, Cotin S, Ayaehe N. A hybrid elastic model allowing real-time cutting, deformations and force-feedback for surgery training and simulation [J]. The Visual Computer, 2000, 10(21): 437-452.

[38] Forest C, Delingette H, Ayache N. Removing tetrahedral from manifold tetrahedralisation: application to real-time surgical simulation [J]. Medical Image Analysis, 2005, 14(9):113-122.

[39] 贾世宇，潘振宽．虚拟手术中基于最少单元分裂的切割仿真技术 [J]. 系统仿真学报, 2008, 20(6): 1488-1492.

[40] Steinemann D, Otaduy MA, Gross M. Fast arbitrary splitting of deforming objects [C] //Cani MP, Brien JO, eds. Proceedings of ACM SIGGRAPH symposium on Computer Animation. Dublin: Eurographics Association, 2006: 63-72.

[41] Courtecuisse H,Jung H, Allard J,etal. GPU-based real-time soft tissue deformation with cutting and haptic feedback [J]. Progress in Biophysics and Molecular Biology, 2010, 103(2-3): 159-168.

[42] Courtecuisse H, Allard J, Kerfriden P,etal. Real-time simulation of contact and cutting of heterogeneous soft-tissues [J]. Medical Image Analysis, 2014, 18(2): 394-410.

[43] Wicke M, Botsch M, Gross M. A finite element method on convex polyhedral [J]. Computer Graphics Forum, 2007, 26(3): 355-364.

[44] Liu GR, Gu YT, 著. 王建明，周学军，译.无网格法理论及程序设计[M].山东:山东大学出版社, 2007.

[45] Guo Xiaohu, Li Xin, Bao Yunfan,etal. Meshless thin-shell simulation based on global conformal parameterization [J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(3): 375-385.

[46] Jung H, Lee DY. Real-time cutting simulation of meshless deformable object using dynamic bounding volume hierarchy [J]. Computer Animation and Virtual Worlds, 2012, 23(5): 489-501.

[47] 朱玲. 虚拟手术中软组织形变与切割技术研究[D]. 哈尔滨：哈尔滨工程大学, 2012.

[48] Ashley H, Adam W, Grand RJ,etal. A meshless Total Lagrangian explicit dynamics algorithm for surgical simulation [J]. International Journal for Numerical Methods in Biomedical Engineering, 2010, 26(8): 977-998.

[49] Grand RJ, Adam W, Karol M. Stable time step estimates for mesh-free particle methods [J]. International Journal for Numerical Methods in Biomedical Engineering, 2012, 91(4): 450-456.

[50] Denis S, Miguel AO, Markus G. Splitting meshless deforming objects with explicit surface tracking [J]. Graphical Models, 2009, 71(1): 209-220.

[51] Shao Xuqiang, Zhou Zhong, Wu Wei. A hybrid deformation model for virtual cutting [C] //Bulterman D, Lee CH, Tsai WH, Liao Mark, eds. 2010 IEEE International Symposium on Multimedia. Taipei: IEEE, 2011: 234-241.

[52] 周喆. 虚拟手术系统中基于混合模型的切割仿真研究 [D]. 上海：上海交通大学, 2012.

[53] Peng Jie, Li Ling, Andrew S. Hybrid surgery cutting using snapping algorithm, volume deformation and haptic Interaction [J]. Journal of Man, Machine and Technology, 2013, 2(1): 35-46.

[54] 贾世宇，潘振宽. 综合使用CPU和GPU的实时手术仿真系统并行框架[J]. 系统仿真学报, 2014, 26(2): 332-338.

[55] Etheredge CE, Kunst EE, Sanders AJB. Harnessing the GPU for real-time haptic tissue simulation [J]. Journal of Computer Graphics Techniques, 2013, 2(2): 28-54.

Research Progress on Soft Tissue Cutting Model for Virtual Surgery Simulation Training System

Cheng Qiangqiang1,3Liu Xiaoping1,2Xu Shaoping1*

1(SchoolofInformationEngineering,NanchangUniversity,Nanchang330031,China)2(SchoolofSystem&ComputerEngineering,CarletonUniversity,OttawaK1S 5B6,Canada)3(SchoolofMeasuring&OpticalEngineering,NanchangHangkongUniversity，Nanchang330063,China)

Virtual surgery simulation training system (VSSTS) solves the problems that exist in the traditional clinician training methods, such as long training period, high cost and lack of training objects. It is a cost-effective alternative training method. As the most common and core type of surgical operations in all kinds of practical surgery, realistically simulating the cutting of soft tissue in real time has always been the difficult and hot issues on studying the virtual surgery simulation system. In this paper, we introduced all kinds of cutting models that have been proposed within the framework of mesh and meshless after giving a brief introduction of the development history of soft tissue cutting model. Then, we analyzed and summarized the advantages and disadvantages of the various modeling method and its applications in the real world virtual surgery simulation systems. In addition, we analyzed the hybrid mode that has been proposed in recent years and gave an outlook for the future of cutting simulation in terms of simulation effect and computing speed.

virtual surgery; soft tissue; cutting model; meshless; hybrid model

10.3969/j.issn.0258-8021. 2015. 04.011

2015-02-09， 录用日期:2015-03-31

国家高技术研究发展计划(863计划) (2013AA013804)；国家自然科学基金(61163023, 51165033)

R318

A

0258-8021(2015) 04-0464-011

*通信作者(Corresponding author)， E-mail: xushaoping@ncu.edu.cn