基于活动轮廓模型的图像分割算法综述

段丁娜 张 欢 邱陈辉 夏顺仁,2#*

1(浙江大学生物医学工程教育部重点实验室，杭州 3100272(浙江省心脑血管检测技术与药效评价重点实验室，杭州 310027)

基于活动轮廓模型的图像分割算法综述

段丁娜1张 欢1邱陈辉1夏顺仁1,2#*

1(浙江大学生物医学工程教育部重点实验室，杭州 3100272(浙江省心脑血管检测技术与药效评价重点实验室，杭州 310027)

活动轮廓模型是一种重要的图像分割技术，它利用底层信息，并结合高层先验知识，实现对复杂目标轮廓的自动分割。自Kass等提出该思想以来的20多年中，活动轮廓模型在理论研究和应用方面均取得长足发展。首先，介绍活动轮廓模型的发展历程，重点阐述并分析典型的参数活动轮廓模型和几何活动轮廓模型，进而扼要介绍混合活动轮廓模型和快速求解算法；随后，从理论基础、分割效果、算法效率以及应用等方面，比较两类模型之间的区别与联系；最后，对活动轮廓模型未来的发展趋势进行展望。

活动轮廓模型；图像分割；参数活动轮廓模型；几何活动轮廓模；混合活动轮廓模型

引言

图像分割对于计算机视觉、模式识别、医学图像处理等具有非常重要的意义，而活动轮廓模型(active contour model)是图像分割的重要工具之一。在传统的计算机视觉领域，Marr分层理论认为，运动跟踪、边缘检测等底层任务是自主的自底向上的过程[1]。但当受到图像噪声、光照阴影等诸多因素的影响时，很多底层任务由于缺乏约束条件而得不到唯一的解。活动轮廓模型的提出，挑战了这种分层理论，在利用底层图像信息的同时，结合高层先验知识，采取的是自上而下的过程，更适合处理个体差异显著、结构复杂的医学图像[2]。该算法首先在图像中初始化一个封闭曲线，然后通过最小化能量泛函，使初始曲线运动到目标对象的边界上，获得图像分割结果。相对于传统图像分割方法，如边缘检测、阈值法、区域生长法等，活动轮廓模型有很多优势[3]：第一，对要检测的目标边界可以达到亚像素精度；第二，可以结合多种先验知识，如形状和灰度分布，很方便地构建特定的能量最小化框架；第三，分割得到的结果是平滑的闭合曲线，对于进一步的形状分析或者目标识别具有重要意义。

活动轮廓模型, 按轮廓线表达形式不同，可以分为参数活动轮廓模型和几何活动轮廓模型。最早的参数活动轮廓模型是1987年由Kass等提出的Snake模型[4]，通过拉格朗日方程将活动轮廓显式地表达为一条带参数的、能量极小化的样条，其能量大小取决于轮廓的初始位置和形状。而最早的几何活动轮廓模型是由Caselles[5]和Malladi[6]等分别提出的一种不含自由参数的隐式测地线活动轮廓模型，应用了曲线进化理论和水平集方法，能够很好地适应曲线拓扑结构的变化。按轮廓线演化方式不同，活动轮廓模型又可分为基于边界的模型和基于区域的模型。基于边界的模型是利用局部边界信息来吸引活动轮廓向着目标边界运动，而基于区域的模型则通过特定的区域描述符来识别不同的感兴趣区域，从而引导活动轮廓的运动。

笔者采取对活动轮廓模型进行分类以及关注各类模型的演变进程的方式进行综述与分析。首先，通过经典的Snake模型以及气球力模型[7]、梯度矢量流模型[8-9]等改进模型，介绍参数活动轮廓模型；接着，着重概述了几何活动轮廓模型的研究现状，包括典型的几何活动轮廓模型及其改进模型、基于边界与区域相结合的混合活动轮廓模型、以活动轮廓模型结合图割的方法为代表的快速求解算法三个方面；最后，对这两类活动轮廓模型从基本原理、分割效果、算法效率、应用方面进行评价与分析，并对该模型的未来进行了展望。

1 参数活动轮廓模型

参数活动轮廓模型(parametric active contour model)，将活动轮廓显式地描述为一条参数化能量曲线，在内力和外力的控制下运动，最终收敛到目标轮廓。其中，内力代表曲线本身的力，控制轮廓线的弯曲和拉伸，而外力是由图像性质决定，吸引轮廓线向期望的图像目标移动。因此，很多学者通过设计新的外力[10]来改进Snake模型。参数活动轮廓模型结合了高层信息，能够实现对目标轮廓的快速有效分割，易于用户交互，在边界检测、形状建模、运动追踪等领域均有很好的应用。

1.1 Snake模型

Snake模型[4]是最先被提出的参数活动轮廓模型，以高斯势力为外力，曲线在高斯势力的指引下向着期望特征运动，到达目标轮廓时，曲线内外的能量加权和最小。将轮廓线位置表示为v(s)=(x(s),y(s))，能量表达式为

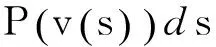
(1)

式中，E(v(s))代表内部能量，使曲线平滑；α(s)为弹力系数；β(s)为强度系数；P(v(s))代表由图像数值特征决定的外部能量，定义为

(2)

式中，ωe是一个正的权因子，Gσ是方差为σ的高斯核函数，I(v(s))为图像灰度。

Snake模型的优点：一是通过尺度空间，由粗到细地极小化能量，扩大了捕获区域，同时降低了计算复杂度，实现了目标轮廓的快速准确分割；二是将边缘、线、目标轮廓等视觉问题都按统一的机制进行处理；三是可以结合更多的高层信息来指导轮廓演化，适合进行用户交互。缺点：一是对初始轮廓的位置敏感，初始化时必须设置在目标轮廓附近；二是其非凸性容易导致陷入局部极小值；三是不能适应曲线的拓扑变化，难以收敛到凹形边界，因此在一定程度上限制了Snake模型的应用范围。

1.2 气球力模型

Cohen等提出了气球力模型[7]。由于在Snake模型中，高斯外力在灰度均匀的区域为零，这样在该区域就缺乏外力的指引作用，活动轮廓会在内力作用下最终收缩为一个点或一条直线。针对这个问题，Cohen等在外力中加入一个动态的、垂直于轮廓曲线且大小恒定的压力(称为气球力)，在一定程度上改善了Snake模型对轮廓边缘的敏感性，并且能够跨越图像中的伪边缘点，收敛到凹形边界。不过，由于膨胀力的驱使，该模型得到的边界有可能会越过实际轮廓。另外，气球力模型仍然存在初始化敏感的问题，如当初始化轮廓与目标边界相交时，很难正确收敛。该模型中的外力定义为

(3)

式中，n(s)为曲线的单位法矢量；k1、k是力的权值，令k略大于k1，使曲线到达边界点时能停止膨胀；P(v)为式(1)中的图像力，定义为P(v)=-|I(v)|2。k1n(s)使活动轮廓膨胀，并稳定地收敛于目标边缘。

1.3 GVF模型及其改进

Xu等提出了梯度矢量流(gradient vector flow, GVF)蛇模型[8-9]，是具有里程碑意义的一种参数活动轮廓模型。该模型引入一种新的静态力——梯度矢量流，作为外力。通过扩散方程扩大了模型的捕获区域，将梯度外力扩展到离目标边界较远的区域，即使在同质区域，仍然有指向边界的矢量，解决了Snake模型对初始轮廓敏感的问题，同时由于扩散过程的固有竞争会产生指向凹形边界的向量，因此GVF能够有效地收敛到深度凹形边界(U型)。但是，GVF方法不能分割狭长的凹形边界，而且仍然没有解决曲线的拓扑变化问题。该模型梯度矢量场的矢量为ν(x,y)=[u(x,y),v(x,y)]，ν(x,y)=-P，能量函数为

(4)

除上述十分典型的3种参数活动轮廓模型外，也有其他学者对参数活动轮廓模型进行过探索。如外力方面， Leroy等的算法中，引入动态的、多分辨率的高斯势力，增大模型的捕获区域，加速了收敛过程[15]；Cohen等提出一种静态的距离势力，能获得与GVF一样大的捕获范围，初始化不敏感，但是它不能收敛到凹形边界[16]。另外， Richard等提出了一种基于统计学理论的Kalman Snake模型，用于刚体和非刚体的运动跟踪领域，以解决线性、高斯问题，并能够得到被跟踪物体的详细信息，如位置、速度、加速度和形状等[17]。Storvik等结合统计学的观点，提出了贝叶斯Snake模型，将最优化问题转化为计算最大后验概率的问题，通过随机采样和模拟退火方案来得到全局最优值，但该算法有收敛速度较慢的缺点[18]。表1对几种典型的参数活动轮廓模型的性能进行了比较。当然，尽管参数活动轮廓模型有多种改进算法，但仍无法解决固有的不能处理曲线拓扑变化等问题，这就为几何活动轮廓模型的提出创造了条件。

表1 几种典型的参数活动轮廓模型的性能对比

2 几何活动轮廓模型

对于几何活动轮廓模型(geometric active contour)，其理论基础是曲线进化理论和水平集[19]思想。该模型的大体思路是，将平面闭合曲线隐含地表达为高维曲面函数的零水平集，通过最小化能量泛函，将曲线的演化方程转化为高维曲面水平集函数的偏微分方程，然后进行迭代演化，使零水平集运动到目标轮廓上去。几何活动轮廓模型解决了参数活动轮廓模型的诸多问题，如几何模型对初始位置不敏感，初始化曲线可以设在任意一个位置而不影响收敛结果；能够处理曲线的多种拓扑变化，灵活地进行分裂、合并；能够得到稳定唯一的数值解，等等。这些优势使得几何活动轮廓模型被广泛地应用于图像处理领域，尤其是被用于处理结构复杂的医学图像。

2.1 典型的几何活动轮廓模型

2.1.1 GAC模型

测地线活动轮廓模型[5](geodesic active contours, GAC)是几何活动轮廓模型初始阶段的标志性模型，是基于边界的活动轮廓模型。该模型提出了基于最小路径计算的目标轮廓检测的新途径，将基于能量最小化的参数活动轮廓模型与基于曲线演化理论的几何活动轮廓模型联系起来，其活动轮廓C(s)的能量泛函为

(5)

式中，L(C)代表曲线C的欧氏长度，g代表停止函数，当曲线运动到目标边界上时停止演化。

根据最速下降法，得到曲线演化方程为

(6)

式中，κ是欧几里得曲率，N是内向法矢量。

2.1.2 CV模型及其算法实现

CV模型是由Chan等提出的基于Mumford-Shah[20]最优分割的活动轮廓模型[21]，是经典的基于区域的几何活动轮廓模型，在处理弱边界时取得了很好的效果，其能量函数为

(7)

式中，L(C)表示曲线C周长，S(C)表示曲线C内部区域面积，μ、v≥0，λ1、λ2>0为能量项权系数，c1和c2分别表示轮廓线C内部区域和外部区域的平均灰度值。当闭合曲线C位于图像区域边界时，能量函数E达到最小值。

引入Heaviside函数和它的导数Dirac函数的平滑形式，有

(8)

(9)

在水平集方法中，用Lipschitz函数φ的零水平集表示轮廓C⊂Ω。结合水平集表示方法后，拟合能量函数E(C,c1,c2)可以写成为

v∬CH(φ(x,y))dxdy+

dxdy

(10)

式中，

(11)

(12)

利用变分法对能量函数极小化，可以得到水平集函数偏微分方程解，即

(13)

式(13)给出了CV算法中隐式活动轮廓φ对时间t的变化量，通过迭代运算，初始轮廓与每次运算的轮廓变化量相加，不断向着目标轮廓运动，最终得到的水平集函数φ为最后的准确分割结果，即

(14)

从能量拟合项中可以看出，最初的CV仅适用于分割包含两个区域的图像，Chan等对此模型进行拓展，通过使用多个水平集函数来代表多个区域，提出分段常数(piecewise constant, PC)模型[22]。然而，由于模型计算的是区域内平均灰度值，因此对于非匀质区域，无论CV还是PC都很难得到准确的分割结果。

为了优化这个问题，Vese[22]等和Tsai[23]等提出了两个相似的基于最小化Mumford-Shah函数框架下的分段平滑(piecewise-smooth, PS)模型。PS模型对非匀质图像有较好的分割效果，而且能实现对三接合处等复杂拓扑结构的分割。但是，PS模型在算法实现的过程中，每隔一定的迭代次数，便要计算两个偏微分方程(partial differential equation, PDE)来更新拟合函数u-、u+，并要把不同区域的u-、u+扩展到整个图像区域；另外，需要周期性地重新初始化退化的水平集函数，因此运算量相当大，收敛速度慢。

2.1.3 LBF模型及其改进

Li等针对CV模型不能有效地分割非匀质区域以及PS模型计算量大的不足，提出了基于局部二值拟合能量(local binary fitting energy, LBF)的隐式活动轮廓模型[24]，也称可伸缩区域拟合能量(region-scalable fitting energy, RSF)模型[3]。该模型将高斯核函数引入数据拟合项，提取局部灰度信息，利用水平集演化，能够得到灰度不均匀图像中的目标轮廓，而且迭代过程中无需重新初始化水平集函数，只需要计算一个PDE。与PS算法相比，该模型大大简化运算量，具有计算简单、能有效处理曲线拓扑变化的优点，适于分割非匀质区域、弱边界以及血管状结构等图像。然而，LBF模型对初始轮廓的位置有一定的敏感性，同时对高噪声图像鲁棒性较差。假定C为图像域Ω中的轮廓曲线，定义Ω中某一点x的能量泛函为

(15)

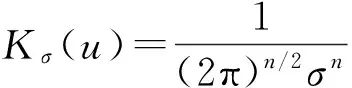
一些学者从不同方面对LBF进行改进，提出多个改进算法。Wang等从局部特性方面对LBF算法进行了改进，提出局部高斯分布拟合(localGaussiandistributionfitting,LGDF)模型[25]，引入了以局部灰度均值和方差为变量的高斯核函数，可用于处理灰度不均匀图像、区分灰度相似但方差不同的纹理区域，以及处理空间强度变化的噪声(如乘性噪声等)，但算法复杂度也因需要估计局部方差而增大了很多，从而限制了该模型的发展。Zhang等从运算效率上对LBF做了改进，提出了局部图像拟合 (localimagefitting,LIF) 能量模型，是继CV、LBF之后又一个被广泛认可的模型[26]。该模型建立了局部拟合图像的能量函数，可以看作是拟合图像与原始图像差异的约束条件，并使用高斯滤波在每一次迭代后正则化水平集函数，运算过程无需进行水平集的重新初始化。与LBF模型相比，LIF模型在能够得到相似的准确率的同时，极大地提高了运算效率。He等对LBF(RSF)算法的局部特性和初始化敏感性进行了改进，提出了加权的可伸缩区域拟合(weightedregion-scalablefitting,WRSF)能量模型[27]。用紧支撑的安抚内核代替LBF中的高斯核，并将局部灰度熵作为权值加入能量积分函数，提高了对同质区域的分割能力，通过适当选取局部区域的半径参数ρ，改善了对初始轮廓的敏感性。

2.1.4LRB模型

Lankton等提出一种基于局部区域(localizingregion-based,LRB)的活动轮廓模型[28]。与LBF模型的实质相类似，利用局部信息，实现了非匀质区域的分割，且容易扩展到多目标图像。该模型构建出一个通用的能量函数框架，理论上，任何基于全局区域的能量函数都可以代入这个框架转化为基于局部区域的能量函数，如CV的统一模型能量[20](uniformmodelingenergy)等。然而，通过局部能量并不能确保得到全局最小值，因此，LRB模型对初始轮廓的位置也有一定的敏感性，同时计算局部信息也在一定程度上延长了算法的执行时间。LRB模型的能量函数为

φ(y))dydx

(16)

式中δ(φ(x))是Dirac函数的一种平滑形式；B(x,y)是局部区域掩模，它的半径要根据待分割目标的尺寸以及周围噪声密度来进行设置；F是通用的内部能量函数，可将其他模型的能量函数相应的局部形式代入。

表2是对几种典型的几何轮廓模型进行的归纳总结。

除上述几个典型的模型外，还有很多学者从不同角度对几何活动轮廓模型进行了研究。Li等提出一种结合空间模糊聚类和水平集的算法[29]。将聚类结果作为水平集的初始轮廓，使水平集可以从逼近真实边界的位置开始演化；同时，通过聚类结果容易估算出水平集面积和长度的比例，据此可以实现水平集参数的自动设置；另外，隶属度信息可以作为定量指标来正则化水平集的演化，在减少人工干预的同时抑制了边界泄露，且提高了计算效率。Michailovich等提出一种由巴式能量函数的梯度流驱动的活动轮廓模型[30]，与传统的基于变分分析并通过最小化能量函数驱动轮廓演化的模型不尽相同，该模型是通过最大化轮廓内外特征向量的概率密度之间的巴式距离(Bhattacharyya distance)来演化轮廓，可以灵活处理多种图像特征，如灰度、颜色以及运动相关特征。Papandreou等通过多重网格法实现水平集的快速演化，采用一个稳定的2-D整合数值方案，对内力使用隐式机制而对外力使用显式机制，增强了算法的灵活性和稳定性,同时该模型具有旋转不变的特性,但分割精度仍有待提高[31]。

表2 典型的几何活动轮廓模型性能对比

2.2 混合活动轮廓模型

近年来，一些学者将基于边界的模型(多采用GAC模型)与基于区域的模型相结合并加以改进，综合利用图像的边界信息与区域信息，得到性能提升的混合活动轮廓模型[32-37]。早期的混合模型[38-40]，是在分割过程中，结合边界的梯度、形状信息与区域的灰度级信息等来改善分割效果。在此，主要介绍近年来将不同模型相结合的新方法。

Zhang等结合GAC与CV的优势，提出一种将水平集函数选择性地二值化、再通过高斯滤波将其正则化 (selective binary and Gaussian filtering regularized level set, SBGFRLS)的模型[32]。利用曲线内外区域的统计信息，构建有符号的压力函数，替代GAC中的边界停止函数，从而控制曲线的演化方向，可以实现对弱边界以及模糊边界的分割，对于局部分割和全局分割都适用，但不能用于分割非匀质区域。Pi等结合GAC和CV模型，采用主成分分析(principal components analysis, PCA)和区间估计，提取目标物体的主要特征，通过判别函数将这些特征融入能量函数中，得到新的变分方程，从而在彩色图像中有针对性地分割出目标物体的内外边界[33]。Liu等将多分段常数的改进CV模型与GAC模型相结合，多分段常数使得CV模型能够处理非同质区域以及彩色图像多目标分割的问题，而使用GAC中的边界指示函数g(C)代替CV中的长度项L(C)，使得模型有更好的边界捕获能力[34]。

Zheng[35]、Dong[36]等将GAC模型与LBF模型相结合，使用图割的方法代替水平集演化。其中，前者引入新的窄带能量函数，通过去除其中的区域项以及用新的局部区域项增强边界项，使模型能够处理背景杂乱的图像和非同质区域的局部分割问题。后者则引入了基于符号距离函数(signal distance function, SDF)的约束项，能对MR大脑图像序列进行高效的分割。另外，Tian等结合了GAC、LBF、SBGFRLS模型，其水平集方程包含了边界相关项、区域相关项和正则项，可以实现对非匀质区域的快速有效分割[37]。

2.3 快速求解算法

几何活动轮廓模型在能量泛函最小化过程中，使用梯度下降法求解，迭代次数多，运算量大，耗费时间长，一些学者提出了多重网格法[31]、窄带法[41]、快速步进法[42]以及加操作分离法[43]等多种水平集快速演化算法，从一定程度上改善了数值计算效率低的问题。

另一种快速求解的思路是将活动轮廓模型与图割方法结合，借助图割(graph cut, GC)计算高效以及全局寻优的能力，代替水平集方法进行轮廓演化，这是近年来活动轮廓研究的热点之一。Boykov等找到了图割与水平集间的联系，认为割的代价函数可以近似于黎曼空间下的轮廓长度或曲面面积，通过将GC与GAC相结合，提出了Geocuts模型[44-45]。Xu等将活动轮廓的迭代形变理论与图割优化方法、窄带法相结合，提出了具有代表性的基于图割的活动轮廓(graph cut based active contour, GCBAC) 模型，通过8邻域连通图中边的权重和来定义代价函数[46-47]。算法过程简述如下：

1)设置初始轮廓ci，将ci进行形态学膨胀，得到CN(contour neighborhood)域；

2)将CN域的内轮廓看做源点，外轮廓看做汇点，通过节点识别过程将多源多汇图转化为单源单汇图；

3)采用s-t最小割方法，得到CN域中的最优轮廓ci+1；

4)将ci+1作为新的初始轮廓重复上述过程，迭代至轮廓不再变化，则找到了全局最优值。

与传统活动轮廓相比，GCBAC具有很多优势：首先，通过GC进行优化，并将轮廓演化限制在CN域中而不计算整幅图像，大大提高了算法效率；其次，GC理论的引入很容易将灰度、颜色、纹理等信息整合到边的权重中去，从而实现对多种图像特征的分割；由于GC计算的是全局最优值，因此对初始轮廓不敏感；另外，该模型还可以分割边界不连续的目标，不会产生自交叉，并允许用户指定一些点进行交互修正。但是，GCBAC只能用于单目标的分割，同时，受最小割的限制，很难分割凹形边界。

另外，Tao提出一种结合了区域信息的GCBAC模型，给出GAC模型基于图割理论的离散表达形式，并将轮廓内外区域的特征信息引入能量函数，实现了对凹形边界和复杂图像的分割，但实现需要注意初始轮廓位置和窄带宽度的适当选取[48]。Chen等提出一种结合二值掩模的GCBAC模型，用于RNAi细胞的自动分割[49]。El-Zehiry等将CV模型改写为基于局部匀质假设的形式[50]，并结合基于GC的水平集方法[51](graph cut based level set, GCBLS)进行优化，实现了对热像图中行人的快速追踪。其中，文献[48-49]以及上面提到的文献[35-36]，都采用将迭代窄带法与图割相结合用于活动轮廓优化的框架，算法的大体流程与GCBAC相似。

3 两类模型评价与分析

由于很多几何活动轮廓模型是由传统的参数活动轮廓模型(Snake)衍变得到的，二者间并没有清晰的界限。文献[52]给出了由标准的参数活动轮廓模型到一般的几何活动轮廓模型的推导过程以及转化公式，精确描述了二者在数值计算过程中的关系，包括空间变化系数、张力和刚度以及非保守的外部力量等，在此不再赘述。由于理论基础不同，参数活动轮廓模型和几何活动轮廓模型在分割效果、算法效率、应用等方面表现出了不同的特点。

参数活动轮廓模型是基于边界信息的模型，其基本思想是通过拉格朗日方程将活动轮廓显式地描述为一条能量极小化的样条，通过结合先验知识设计不同的外力，如高斯势力、压力、气球力、梯度向量流等，可以使模型的性能得到提升。而几何活动轮廓模型除GAC外大多是基于区域信息的模型，其理论基础是曲线进化理论和水平集方法，将活动轮廓隐式地描述为高维曲面的零水平集，可以通过改进核函数更好地利用全局和局部信息，从而提升模型的性能。

在分割效果方面，参数模型具有一定的抗噪声干扰能力，能够克服边缘狭缝。通过气球力模型、GVF模型的改进，参数模型在匀质区域以及曲率高的U形区域也能够准确收敛。另外，参数模型允许用户通过高层机制指定演化过程中经过的点，可以用于交互操作。但除GVF外，大部分的参数模型对初始曲线的位置较敏感，当初始轮廓远离目标轮廓时，难以检测到目标内部和外部的轮廓，容易得到局部最小值，因此初始轮廓必须设置在目标轮廓附近。另外，由于一组参数只能表示一条曲线，参数模型不能处理曲线的拓扑变化，只能分割单目标图像。几何模型与参数模型相比有很大改进，其特点是对初始轮廓不敏感，具有全局搜索能力，任意设置初始轮廓都可找到相似的分割结果，有利于批量图像的自动处理。同时，水平集的引入使得该模型能灵活处理曲线的拓扑变化，自由地进行分裂、合并，可以分割多目标图像。通过LBF、LRB、LIF等模型的改进，使非匀质区域以及噪声、纹理图像也能得到很好的分割效果。但该模型不适于进行交互操作，而且对于有缺口的轮廓容易发生边界泄露而得不到理想结果。

在算法效率方面，参数模型由于采用显式描述曲线的方法，且在尺度空间上采取由粗到细的方式进行能量极小化，降低了运算复杂度，适合进行快速分割。而几何模型因为采用隐式的曲线描述方法，计算量增大，尤其是PS等模型，算法效率低；经过 LBF、LIF等模型的改进，以及结合窄带法、图割等快速求解方法，算法效率有了一定的提高。

从应用来看，参数模型和几何模型在分割、边界检测和运动追踪等领域均有成功的应用。近年来，参数模型被用于虹膜[53]、视网膜血管[54]、心血管[55]等医学图像分割，以及细胞骨架纤维的分割与追踪[56]等方面。几何模型被用于PET[57]、MR[58]、CT[59-60]、X光[61]等医学图像和航拍图像[62]、卫星图像[63]的分割，还被应用于多目标检测[34]和视觉追踪[64]等方面。

总体来看，近几年有关几何模型的研究相对较多，应用也更广泛一些。但针对具体问题，需根据实际情况进行分析，权衡模型性能与问题需求，选取合适类型的活动轮廓模型算法。

4 结论与展望

活动轮廓模型近年来广受关注，许多学者对此进行了研究，衍生出多种不同的算法。发展至今，活动轮廓模型已经成为图像分割技术中一个重要的方法，且被广泛用于复杂医学图像、遥感图像的分割，以及运动追踪领域。未来的研究，可以着眼于以下几个方面：设计新的外力和核函数，使模型获得更有效的全局或局部信息；除图割、窄带法以外，尝试与采用新的快速求解方法来提升算法效率；探索利用边界梯度信息和区域灰度信息以外的更多信息，如利用纹理信息等来构建能量函数。另外，将更多地关注复杂背景下的彩色图像、多目标图像的分割问题，设计适于这些问题处理的活动轮廓模型。可以相信，随着该领域研究的不断深入，活动轮廓模型将在更广泛的领域发挥出更大的作用。

[1] Marr D. A computational investigation into the human representation and processing of visual information [M]. San Francisco: W H Freeman and Company, 1982.

[2] 李培华，张田文. 主动轮廓线模型(蛇模型)综述 [J]. 软件学报, 2000, 11(6): 751-757.

[3] Li Chunming, Kao CY, Gore J,etal. Minimization of region-scalable fitting energy for image segmentation [J]. IEEE Transactions on Image Processing, 2008, 17(10): 1940-1949.

[4] Kass M, Witkin A, Terzopoulos D. Snakes: active contour models [J]. International Journal of Computer Vision, 1988, 1(4): 321-331.

[5] Caselles V, Kimmel R, Sapiro G. Geodesic active contours [J]. International Journal of Computer Vision, 1997, 22(1): 61-79.

[6] Malladi R, Sethian JA, Vemuri BC. Shape modeling with front propagation: a level set approach [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(2): 158-175.

[7] Cohen LD. On active contour models and balloons [J]. CVGIP: Image Understanding, 1991, 53(2): 211-218.

[8] Xu Chenyang, Prince JL. Snakes, shapes, and gradient vector flow [J]. IEEE Transactions on Image Processing, 1998, 7(3): 359-369.

[9] Xu Chenyang, Prince JL. Generalized gradient vector flow external forces for active contours [J]. Signal Processing, 1998, 71(2): 131-139.

[10] 张丽飞，王东峰，时永刚，等. 基于形变模型的图像分割技术综述 [J]. 电子与信息学报, 2003, 25(3): 395-403.

[11] Hafiane A, Vieyres P, Delbos A. Phase-based probabilistic active contour for nerve detection in ultrasound images for regional anesthesia [J]. Computers in Biology and Medicine, 2014, 52(1): 88-95.

[12] Ma Li, Su Tianzhen. Contour extraction of skin tumors using visual attention and GVF-snake model [J]. Engineering, 2013, 5(10): 482-486.

[13] Rodtook A, Makhanov SS. Multi-feature gradient vector flow snakes for adaptive segmentation of the ultrasound images of breast cancer [J]. Journal of Visual Communication and Image Representation, 2013, 24(8): 1414-1430.

[14] Ko BC, Gim JW, Nam JY. Automatic white blood cell segmentation using stepwise merging rules and gradient vector flow snake [J]. Micron, 2011, 42(7): 695-705.

[15] Leroy B, Herlin IL, Cohen LD. Multi-resolution algorithms for active contour models [C] //Berger MO, Deriche R, eds. The 12th International Conference on Analysis and Optimization of Systems Images, Wavelets and PDEs. Paris: Springer Berlin Heidelberg, 1996: 58-65.

[16] Cohen LD, Cohen I. Finite-element methods for active contour models and balloons for 2-D and 3-D images [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 11(15): 1131-1147.

[17] Szeliskit R, Terzopoulos D. Physically-based and probabilistic models for computer vision [C] //Vemuri BC, eds. SPIE: Geometric Methods in Computer Vision. San Diego: Society of Photo-Optical Instrumentation Engineers, 1991: 140-152.

[18] Storvik G. A Bayesian approach to dynamic contours through stochastic sampling and simulated annealing [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(10): 970-986.

[19] Osher S, Sethian JA. Fronts propagating with curvature dependent speed: algorithms based on Hamilton-Jacobi formulations [J]. Journal of Computational Physics, 1988, 79(1): 12-49.

[20] Mumford D, Shah J. Optimal approximation by piecewise smooth function and associated variational problems [J]. Communication on Pure and Applied Mathematics, 1989, 42(5): 577-685.

[21] Chan TF, Vese LA. Active contours without edges [J]. IEEE Transactions on Image Processing, 2001, 10(2): 266-277.

[22] Vese LA, Chan TF. A multiphase level set framework for image segmentation using the mumford and shah model [J]. International Journal of Computer Vision, 2002, 50(3): 271-293.

[23] Tsai A, Yezzi Jr A, Willsky AS. Curve evolution implementation of the mumford-shah functional for image segmentation, denoising, interpolation, and magnification [J]. IEEE Transcations on Image Processing, 2001, 10(8): 1169-1186.

[24] Li Chunming, Kao CY, Gore JC,etal. Implicit active contours driven by local binary fitting energy [C] //Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis: IEEE, 2007: 1-7.

[25] Wang Li, He Lei, Mishra A,etal. Active contours driven by local Gaussian distribution fitting energy [J]. Signal Processing, 2009, 89(12): 2435-2447.

[26] Zhang Kaihua, Song Huihui, Zhang Lei. Active contours driven by local image fitting energy [J]. Pattern Recognition, 2010, 43(4): 1199-1206.

[27] He Chuanjiang, Wang Yan, Chen Qiang. Active contours driven by weighted region-scalable fitting energy based on local entropy [J]. Signal Processing, 2012, 92(2): 587-600.

[28] Lankton S, Tannenbaum A. Localizing region-based active contours [J]. IEEE Transactions on Image Processing, 2008, 17(11): 2029-2039.

[29] Li Bingnan, Chui CK, Chang S,etal. Integrating spatial fuzzy clustering with level set methods for automated medical image segmentation [J]. Computers in Biology and Medicine, 2011, 41(1): 1-10.

[30] Michailovich O, Rathi Y, Tannenbaum A. Image segmentation using active contours driven by the Bhattacharyya gradient flow [J]. IEEE Transactions on Image Processing, 2007, 16(11): 2787-2801.

[31] Papandreou G, Maragos P. Multigrid geometric active contour models [J]. IEEE Transactions on Image Processing, 2007, 16(1): 229-240.

[32] Zhang Kaihua, Zhang Lei, Song Huihui,etal. Active contours with selective local or global segmentation: A new formulation and level set method [J]. Image and Vision Computing, 2010, 28(4): 668-676.

[33] Pi Ling, Shen Chaoming, Li Fang,etal. A variational formulation for segmenting desired objects in color images [J]. Image and Vision Computing, 2007, 25(9): 1414-1421.

[34] Liu Liman, Tao Wenbing, Liu Jin,etal. A variational model and graph cuts optimization for interactive foreground extraction [J]. Signal Processing, 2011, 91(5): 1210-1215.

[35] Zheng Qiang, Dong Enqing, Cao Zhulou,etal. Modified localized graph cuts based active contour model for local segmentation with surrounding nearby clutter and intensity inhomogeneity [J]. Signal Processing, 2013, 93(4): 961-966.

[36] Dong Enqing, Zheng Qiang, Sun Wenyan,etal. Constrained multiplicative graph cuts based active contour model for magnetic resonance brain image series segmentation [J]. Signal Processing, 2014, 104: 59-69.

[37] Tian Yun, Duan Fuqing, Zhou Mingquan,etal. Active contour model combining region and edge information [J]. Machine Vision and Applications, 2013,24(1): 47-61.

[38] Song Chunzhu, Yuille A. Region competition: unifying snakes, region growing, and Bayes/MDL for multiband image segmentation [J]. IEEE Transactions on Patteren Analysis and Machine Intelligence, 1996, 18(9): 884-900.

[39] Chakraborty A, Staib LH, Duncan JS. Deformable boundary finding in medical images by integrating gradient and region information [J]. IEEE Transactions on Image Processing, 1996, 15(6): 859-870.

[40] Paragios N, Deriche R. Geodesic active regions and level set methods for supervised texture segmentation [J]. International Journal of Computer Vision, 2002, 46(3): 223-247.

[41] Caselles V, Catté F, Coll T,etal. A geometric model for active contours in image processing [J]. Numerische Mathematik, 1993, 66(1): 1-31.

[42] Sethian JA. A fast marching level set method for monotonically advancing fronts [J]. Proceedings of the National Academy of Sciences, 1996, 93(4): 1591-1595.

[43] Weickert J, Romeny BMTH, Viergever MA. Efficient and reliable schemes for nonlinear diffusion filtering [J]. IEEE Transactions on Image Processing, 1998, 7(3): 398-410.

[44] Boykov Y, Kolmogorov V. Computing geodesics and minimal surfaces via graph cuts [C] //Proceedings of the 9th IEEE International Conference on Computer Vision. Nice: IEEE, 2003: 26-33.

[45] Boykov Y, Kolmogorov V, Cremers D,etal. An integral solution to surface evolution PDEs via geo-cuts [C] //Leonardis A, Bischof H, Pinz A, eds. Proceedings of the 9th European Conference on Computer Vision. Graz: Springer Berlin Heidelberg, 2006: 409-422.

[46] Xu Ning, Bansal R, Ahuja N. Object segmentation using graph cuts based active contours [C] //Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Madison: IEEE, 2003: 46-53.

[47] Xu Ning, Ahuja N, Bansal R. Object segmentation using graph cuts based active contours [J]. Computer Vision and Image Understanding, 2007, 107(3): 210-224.

[48] Tao Wenbing. Iterative narrowband-based graph cuts optimization for geodesic active contours with region forces (GACWRF) [J]. IEEE Transactions on Image Processing, 2012, 21(1): 284-296.

[49] Chen Cheng, Li Houqiang, Zhou Xiaobo,etal. Constraint factor graph cut-based active contour method for automated cellular image segmentation in RNAi screening [J]. Journal of Microscopy, 2008, 230(2): 177-191.

[50] El-Zehiry N, Elmaghraby A. A graph cut based active contour without edges with relaxed homogeneity constraint [C] //The 19th International Conference on Pattern Recognition. Tampa: IEEE, 2008: 1-4.

[51] El-Zehiry N, Xu S, Sahoo P,etal. Graph cut optimization for the Mumford-Shah model [C] //Villanueva JJ, eds. Proceedings of the 7th IASTED International Conference Visualization, Imaging, and Image Processing. Anaheim: ACTA Press, 2007: 182-187.

[52] Xu Chengyang, Yezzi Jr A, Prince JL. On the relationship between parametric and geometric active contours [C] //Conference Record of the 34th Asilomar Conference on Signals, Systems, and Computers. Pacific Grove: IEEE, 2000: 483-489.

[53] Nguyen K, Fookes C, Sridharan S. Fusing shrinking and expanding active contour models for robust iris segmentation [C] //Proceedings of the 10th International Conference on Information Sciences Signal Processing and their Applications(ISSPA). Kuala Lumpur: IEEE, 2010: 185-188.

[54] Al-Diri B, Hunter A, Steel D. An active contour model for segmenting and measuring retinal vessels [J]. IEEE Transactions on Medical Imaging, 2009, 28(9): 1488-1497.

[55] 孙丰荣，刘泽，李艳玲，等. 一种改进的自适应形变模型及其血管内超声图像边缘提取应用 [J]. 中国生物医学工程学报, 2008, 27(2): 276-281.

[56] Smith MB, Li Hongsheng, Shen Tian,etal. Segmentation and tracking of cytoskeletal filaments using open active contours [J]. Cytoskeleton, 2010, 67(11): 693-705.

[57] Abdoli M, Dierckx R, Zaidi H. Contourlet-based active contour model for PET image segmentation [J]. Medical Physics, 2013, 40(8): 082507.

[58] Zhu Wei, Kang SH, Biros G. A geodesic-active-contour-based variational model for short-axis cardiac MR image segmentation [J]. International Journal of Computer Mathematics, 2013, 90(1): 124-139.

[59] Qian Xiaohua, Wang Jiahui, Guo Shuxu,etal. An active contour model for medical image segmentation with application to brain CT image [J]. Medical Physics, 2013, 40(2): 021911.

[60] Foruzan AH, Chen Yenwei, Zoroofi RA,etal. Segmentation of liver in low-contrast images using K-means clustering and geodesic active contour algorithms [J]. IEICE Transactions on Information and Systems, 2013, 96(4): 798-807.

[61] Hao Xin, Shen Ye, Xia Shunren. Automatic mass segmentation on mammograms combining random walks and active contour [J]. Journal of Zhejiang University Science C, 2012, 13(9): 635-648.

[62] Ahmadi S, Zoej MJ, Ebadi H,etal. Automatic urban building boundary extraction from high resolution aerial images using an innovative model of active contours [J]. International Journal of Applied Earth Observation and Geoinformation, 2010, 12(3): 150-157.

[63] Celik T, Ma Kaikuang. Multitemporal image change detection using undecimated discrete wavelet transform and active contours [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 706-716.

[64] Hu Weiming, Zhou Xue, Li Wei,etal. Active contour-based visual tracking by integrating colors, shapes, and motions [J]. IEEE Transactions on Image Processing, 2013, 22(5): 1778-1792.

A Review of Active Contour Model Based Image Segmentation Algorithms

Duan Dingna1Zhang Huan1Qiu Chenhui1Xia Shunren1,2#*

1(KeyLaboratoryofBiomedicalEngineeringofMinistryofEducation,ZhejiangUniversity,Hangzhou310027,China)2(ProvincialKeyLaboratoryofCardio-CerebralVascularDetectionTechnologyandMedicinalEffectivenessAppraisal,Hangzhou310027,China)

Active contour model is an important method for image segmentation. It combines underlying information with high-level prior knowledge to achieve automatic segmentation for complex objects. Active contour model has been developed greatly in theory research and application, since it was proposed twenty years ago. This paper reviewed the development process of active contour model at first and describes the classical parametric active contour models and geometric active contour models, and presents briefly new hybrid active contour models as well as fast solution algorithms. After that, the relationship between these two kinds of models through theory basis, performance, efficiency and applications were introduced. The future prospect of active contour model was discussed as well.

active contour model; image segmentation; parametric active contour model; geometric active contour model; hybrid active contour model

10.3969/j.issn.0258-8021. 2015. 04.009

2014-12-17， 录用日期:2015-05-11

国家“十二五”科技支撑计划资助项目(2012BAI10B04)；国家自然科学基金(81101903)

R318

A

0258-8021(2015) 04-0445-10

# 中国生物医学工程学会会员(Member, Chinese Society of Biomedical Engineering)

*通信作者(Corresponding author)， E-mail: srxia@zju.edu.cn