雷达的威力图的计算机绘制
2015-09-11孙国政
孙国政


摘要:对经典雷达方程进行了仔细的分析,并推算出其与仰角的内在关系。在此基础上,对距离-高度-仰角的关系也进行了详细的推导。雷达方程及距离-高度-仰角关系,可反映雷达探测距离与仰角之间的内在联系。在此基础上,总结了雷达威力图的绘制方法,并推算出计及地面反射的雷达威力图方程。最后,以堆积多波束雷达为例,结合地面反射系数,进行了雷达威力图绘制的演示。
关键词:威力图;地面反射;堆积多波束
中图分类号:TP391 文献标识码:A 文章编号:1009-3044(2015)17-0218-03
Air Coverage Computer Plotting For Surveillance Radar
SUN Guo-zheng
(Unit 91404 of PLA, Qinhuangdao 066000, China)
Abstract: The paper gives detailed discussion of radar equations as well as the internal relationship between range and elevations. According to the discussions, range-height-angle relationship is derived. The method of plotting air coverage is summarized, also including reflection propagation on surface. In the end, the paper demonstrates plotting of air coverage chart of surface-based surveillance radar both in free space and in earth surface.
Key words: air coverage chart reflection stack-beams
监视雷达最主要的测量参数为:斜距、方位以及仰角(高度)。雷达威力图是距离、仰角及高度三者的联合表示。严格地说,单独的自由空间作用距离是不能表示雷达的探测性能的[1]。为了更好的考核雷达的性能,引入了雷达威力图。雷达的威力图是雷达方程的全息表示,它是反映雷达在垂直覆盖范围的全部探测性能。雷达威力图由雷达威力曲线界定。雷达威力曲线是反映雷达作用斜距、仰角及高度三者关系的曲线;雷达威力图是指由威力曲线包围的闭合平面图。雷达威力图的模型极为复杂。人们一般将雷达的威力模型进行简化得到,随着计算机技术的发展,威力图将可以更为精确的绘制。本文即利用计算机仿真技术对威力图进行精确的绘制。
1 雷达方程的基本形式
雷达方程是雷达设计的核心,也是威力图绘制的基石。雷达方程有很多种,但最为基本的方程如下所示[2]。
[R4m=PtτGtGrλ2σF2rF2t4π3kTsDx(n)LsLα] (1)
式中:Pt为峰值功率,r为脉冲宽度,Gt为发射增益,Gr为接收增益,[σ]为目标截面积,[F2t],[F2r]分别为天线发射与接收方向图传播因子,k为玻尔兹曼常数,为1.3810-23,Ts为系统噪声温度单位为K,Dx(n)为n个脉冲非相参积累条件下对应的单脉冲检测因子,Ls为系统总损耗;L为大气传播损耗。在上式中,[F2t],[F2r],Ts,Ls,L等是仰角的函数。因此,上式可以写成[R=f(θ)],即雷达探测威力是仰角的函数。
2 距离、仰角与高度的关系
雷达测量的仰角、距离及高度存在一定的关系。主要有两个方面:一是地球曲率,二是地面反射。地面反射在低频段,如米波以下,特别明显[2]。没有考虑地面反射的雷达威力图是不充分的。地面反射条件下,绘制雷达威力图主要考虑地面反射系数引起的干涉效应、绕射效应、植被覆盖、地形地貌等多种影响因素[3],为简化计,将地球考虑成为一个球形,上述两方面分析如图1所示。
[G=aearccosae+hr2+ae+ht2-R22(ae+hr)(ae+hr)≈aearcsinRae] (2)
式中,[ae] 为地球有效半径,取8494千米,R为目标斜距,G为地面距离。
对于搜索警戒雷达,由于R一般在几百千米左右,故而R/ae很小,可得GR,即地面距离与斜距近似的相等。因此,威力图中,横坐标选择斜距正好反映了斜距与地面距离的内在关系。但是,对于空中目标,其斜距与仰角有一定的关系,如下。
[Rht,θ0=h0htdh1-nh0cosθ0/nh(1+(h-h0)/a)2] (3)
式中,[θ0]为离开雷达的仰角,ht为目标高度,h0为雷达的海拔高度,n(h)为在高度为h时的大气折射系数,a为地球半径。公式(4)通过大气折射系数,可以精确解算出斜距、仰角及高度的对应值。该公式比较复杂,可通过数值分析的办法实现。
3 雷达威力图基本曲线的绘制
雷达威力图中X、Y坐标规定如下[4]:
[x=R(θ)cosθ] (4)
[y=R(θ)sinθ] (5)
根据工程要求,可以对x,y设置一定的比例。雷达威力图参考曲线主要有四种曲线构成,它们是等距线、等高线、等仰角线和威力曲线。其中,前三条曲线又称为参考线。公式(3)反映了空间点斜距、仰角与高度之间的几何关系。雷达威力图为一条由仰角范围及其对应雷达斜距决定的一条曲线(在采用长短脉冲的雷达中,一般由两条以上曲线组成)围成的面。确切地说,对于工作于多种模式下的雷达,每一个功能模式一般对应一条曲线。该曲线与坐标原点构成一条闭合的曲线,曲线围成的面即为威力覆盖图。
综上所述,雷达威力图的绘制流程如下:等距线->等高度线->等仰角线->威力曲线。
以上前三步骤为绘制雷达威力图的基础。
(1)等距离线的绘制
根据最大探测威力及仪表距离,选定拟绘制的等距线,如仪表距离为350公里,在斜距0~350公里范围内,选择0 50 100350值作为拟绘制的曲线的点。表示为向量形式R=[0 50 100350]T。适当选择威力范围内的仰角,地面(舰载)雷达范围为0~90度;机载或天基雷达,则选择的角度范围将涉及负角度。如要绘制地基威力图,则有:[θ]=[0 0.1 0.290]T。
根据公式(5)、(4),可以得出等距离线在X,Y轴上的坐标为:
[XR=R×cosθ×π180]
[YR=R×sinθ×π180]
其中XR,YR均为矩阵,矩阵的每一行对应一条等距离线的X,Y轴的坐标向量。因此,可以绘制8条等距离线。
(2)等高度线的绘制
根据最大探测高度,选定拟绘制的等高线,如威力覆盖为40千米,则可选择大于40千米的一个高度作为绘制上限。取高度向量为:h=[0 2 440]T。距离向量取值与等距离线相对应。则对应不同高度与斜距的仰角为:
[θij=arcsinhtiRj-Rj2ae] [i=1,2,…,21;j=1,2,…,8] (6)
公式(7)可以形成一个仰角矩阵[θ],共21行,8列。根据公式(5)、(6)可以得到等高度线在X轴、Y轴上的坐标矩阵Xθ,Yθ,其每个元素为:
[xθij=Rjcos (θij)]
[yθij=Rjsin (θij)]
Xθ,Yθ的每一行对应一条曲线,共21条等高线。
(3)等仰角线的绘制。
等仰角线的绘制与等距离线的绘制类似。根据公式(6)、(7),所有等仰角线的坐标定义如下。仰角向量为:
[xθ=R×cosθ]
[yθ=R×sinθ]
该矩阵的每一个列向量对应一条等仰角线。由于威力图的非线性特征,仰角的选择将不是均匀的[4]。
4 雷达威力曲线绘制
公式(1)不能全面反映雷达威力图,可以将公式(1)改写为如下形式[2]。
[R4m(θ)=PtτGtGrλ2σF2r(θ)F2t(θ)4π3kTs(θ)Dx(n)Ls(θ)] (7)
式中,[F2t(θ)]为发射方向图传播因子,一般有如下形式,笔形波束、赋形波束。另外,该因子还与地面反射有关。[F2r(θ)]为接收方向图因子,一般采用笔形波束或赋形波束。如堆积多波束雷达的发射方向图为赋形图形,接收方向图为多个笔形波束,每个笔形波束的空间指向不同,互相堆叠充满整个发射宽波束。其目的是通过比较各个接收波束回波信号,即可得到目标的仰角值,并进而推算出目标的高度值。
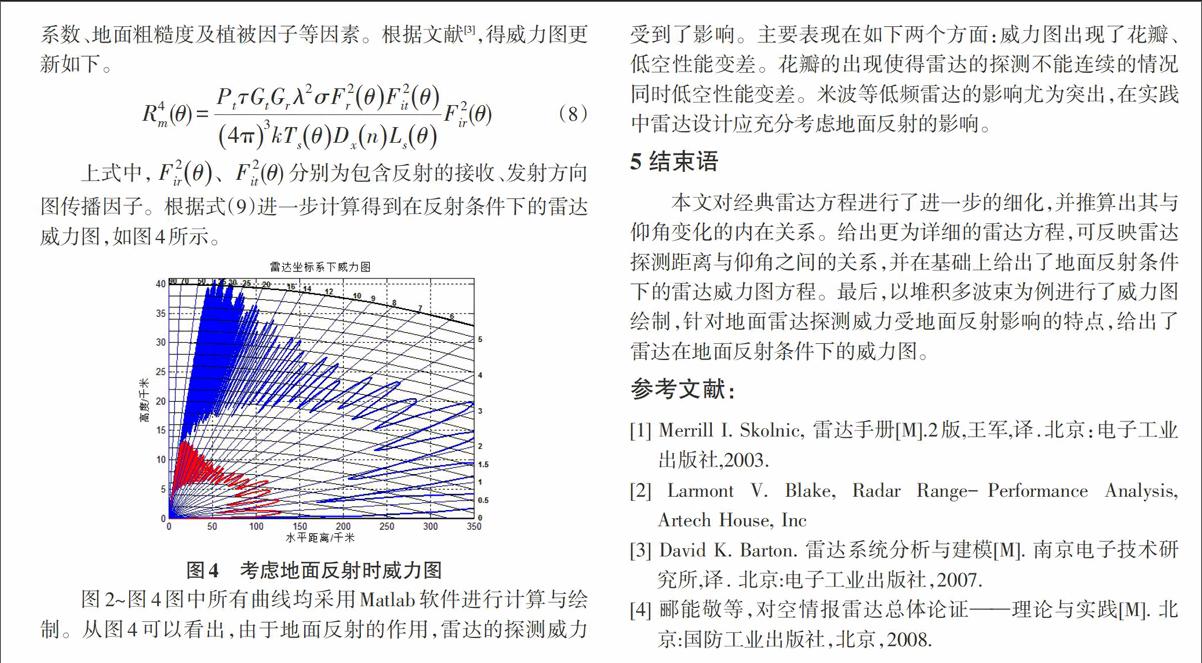
下面绘制一个典型的堆积多波束雷达威力图。距离、高度与仰角的关系使用公式(5)表示。该雷达的仰角覆盖为70度,高度覆盖为40千米,发射采用赋形宽波束,覆盖到70度仰角;接收采用堆积多波束,共12个波束排列如下图所示。其自由空间距离为300公里,采用长短脉冲技术,短脉冲用于补盲,威力图为内部曲线,分别为长短脉冲威力示意图。
图2~图4图中所有曲线均采用Matlab软件进行计算与绘制。从图4可以看出,由于地面反射的作用,雷达的探测威力受到了影响。主要表现在如下两个方面:威力图出现了花瓣、低空性能变差。花瓣的出现使得雷达的探测不能连续的情况同时低空性能变差。米波等低频雷达的影响尤为突出,在实践中雷达设计应充分考虑地面反射的影响。
5 结束语
本文对经典雷达方程进行了进一步的细化,并推算出其与仰角变化的内在关系。给出更为详细的雷达方程,可反映雷达探测距离与仰角之间的关系,并在基础上给出了地面反射条件下的雷达威力图方程。最后,以堆积多波束为例进行了威力图绘制,针对地面雷达探测威力受地面反射影响的特点,给出了雷达在地面反射条件下的威力图。
参考文献:
[1] Merrill I. Skolnic, 雷达手册[M].2版,王军,译.北京:电子工业出版社,2003.
[2] Larmont V. Blake, Radar Range-Performance Analysis, Artech House, Inc
[3] David K. Barton. 雷达系统分析与建模[M]. 南京电子技术研究所,译. 北京:电子工业出版社,2007.
[4] 郦能敬等,对空情报雷达总体论证——理论与实践[M]. 北京:国防工业出版社,北京,2008.
