巧用平移不变性，画出正方体的展开图

吴洁华

在学习简单的立体图形时，有一项很有意思的作业：画出正方体的所有展开图.每个同学都可以毫不犹豫地画出开头几个，但要画出所有11个不全等的展开图，可真要动一点脑筋，否则不是漏掉了就是重复了，简直毫无章法可言.我们在这里介绍一种做法，可以让你有顺序地画出所有的正方体展开图而不必记忆，甚至还可以发现不同展开图之间是存在联系的.

首先，我们不难画出下面“T”字形的展开图，除了标有数字1的另外的5个正方形可以拼成一个无盖的正方体.让方块1在立体图形上沿着A-B-C-D的位置连续翻转，可以得到不同的展开图.对应于左边的展开图，我们可以认为：方块1沿着AD的方向平移，可以得到不同形状的展开图.我们把这个结论称为“平移不变性”.

利用这个性质，我们每次改变一个正方形的位置，就可以得到几乎所有正方体的展开图.首先，让方块1和2改变相对位置，得到以下6种展开图.

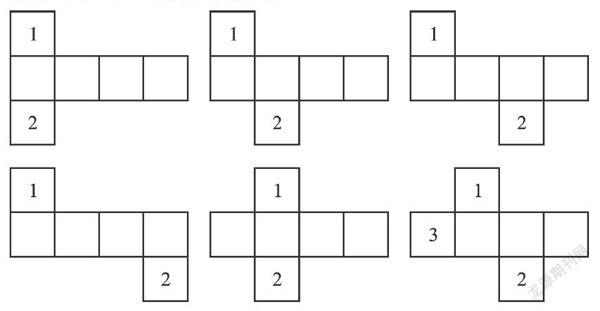
接下来，把上图最后一个标号为3的正方体向上平移一格，得到下面的展开图.

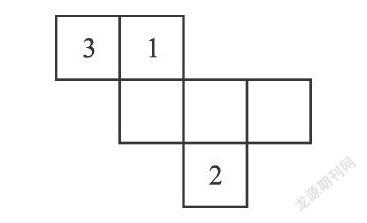
这个过程可以继续进行，但要注意，每次只能平移一个方块，且只能沿着棱的方向平移.

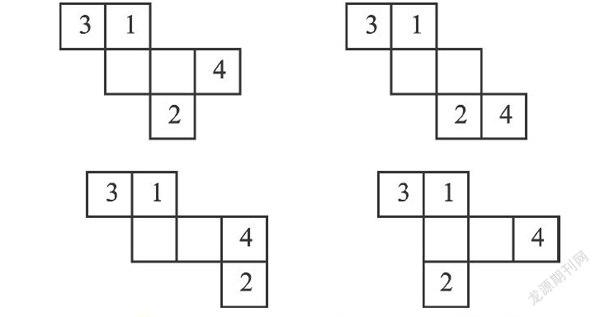
这样，我们连续得到了正方体的10个展开图，你会发现，这10个图形之间可以互相通过我们这里所讲的平移变换得到，因此不需要刻意去记忆它们的形状.为了增强学习的体验，建议同学们用几张硬纸板做一下实验.

最后，还有一个展开图比较特殊，我们单独画在下面.

学习过程中，需要主动思考，发现问题的特征和规律.如果你不主动思考，没有人会告诉你怎么办，你也就享受不到学习的乐趣，体验不了开发智慧的成就感，愿我们共勉！

（作者单位：江苏省南师附中江宁分校）