源于生活服务生活

周小伟

在日常生活中，统计和概率的简单应用比较普遍，几乎无处不在，如买彩票、掷骰子、游戏是否公平、预测销售量等，这些大家非常熟悉的游戏或者活动，都可以由同学们自己动手实验，建立统计和概率的模型，通过简单的计算得到一个合理的解释或正确的预测. 在近几年的中考数学试题中，统计和概率的简单应用都作为一个重要的知识点进行考查，立意新颖，分值较大，突出了数学应用于生活的理念，得到大家的高度重视，下面结合这一章的知识分类评析.

一、 统计的合理性

在进行数据的收集、整理、统计和分析时，常常需要抽取一个合理的样本，根据样本的情况估计总体的情况，解决这类问题的关键是要体会收集数据结果的不确定性和多样性，理解抽样的必要性以及样本抽取的合理性，再根据抽取的样本，运用统计的知识进行合理的预测.

例1 （2014·南京）为了了解某市120 000名初中学生的视力情况，某校数学兴趣小组收集有关数据，并进行整理分析.

（1） 小明在眼镜店调查了1 000名初中学生的视力，小刚在邻居中调查了20名初中学生的视力，他们的抽样是否合理？并说明理由.

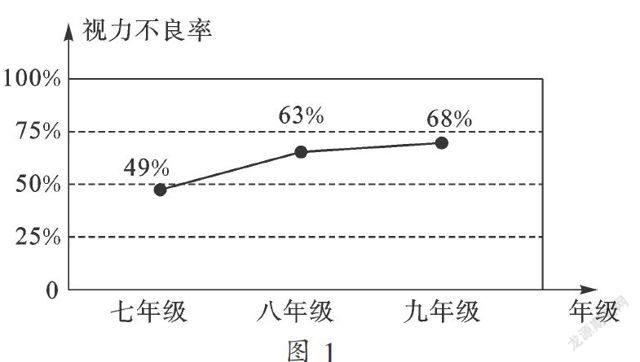
（2） 该校数学兴趣小组从该市七、八、九年级各随机抽取了1 000名学生进行调查，整理他们的视力情况数据，得到如下的折线统计图（如图1）.

请你根据抽样调查的结果，估计该市120 000名初中学生视力不良的人数是多少？

【分析】（1） 他们的抽样都不合理. 因为如果1 000名初中学生全部在眼镜店抽取，那么该市每个学生被抽到的机会不相等，样本不具有代表性，如果只抽取20名初中学生，那么样本的容量过小，样本不具有广泛性.

（2） 根据题意得：

×120 000=72 000（名），

该市120 000名初中学生视力不良的人数是72 000名.

【点评】此题考查的知识点是抽样调查的可靠性、用样本估计总体以及折线统计图. 解决此题的关键是要理解样本的合理抽取直接关系到对总体估计的精准程度，抽取的样本必须同时具有代表性和独立性，同时读懂统计图，从不同的统计图中得到必要的信息也是解决问题的关键.

例2 （2014·江苏南通）九年级（1）班开展了为期一周的“敬老爱亲”社会活动，并根据学生做家务的时间来评价他们在活动中的表现，老师调查了全班50名学生在这次活动中做家务的时间，将统计的时间（单位：小时）分成5组：

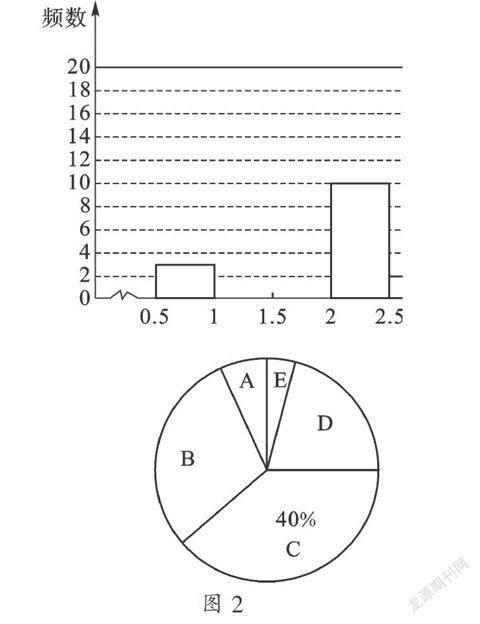
A. 0.5≤x<1；B. 1≤x<1.5；C. 1.5≤x<2；D. 2≤x<2.5；E. 2.5≤x<3；并制成两幅不完整的统计图（如图2）：

请根据图中提供的信息，解答下列问题：

（1） 这次活动中学生做家务时间的中位数所在的组是______；

（2） 补全频数分布直方图；

（3） 该班的小明同学这一周做家务2小时，他认为自己做家务的时间比班里一半以上的同学多，你认为小明的判断符合实际吗？请用适当的统计知识说明理由.

【分析】（1） C组的人数是：50×40%=20（人），B组的人数是：50-3-20-10-2=15（人），把这组数据按从小到大排列，由于共有50个数，第25、26位都落在1. 5≤x<2范围内，则中位数落在C组，故答案为：C；

（2） 根据（1）得出的数据补图如图3：

（3） 符合实际.

设中位数为m，根据题意，m的取值范围是1.5≤m<2，

∵小明帮父母做家务的时间大于中位数，∴他帮父母做家务的时间比班级中一半以上的同学多.

【点评】本题考查频数分布直方图的读图能力和利用统计图获取信息的能力. 利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决相关问题.

二、 规则的公平性

概率与我们的日常生活息息相关，它能解决一些简单的实际问题，帮助我们作决定，作估计，解释一些实验现象，澄清日常生活中的一些错误认识，解决这类问题的关键是要把一些实际问题转化为概率模型，体会概率模型的作用以及运用概率思考问题的特点.

例3 （2014·江苏盐城）如图4所示，可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等.

（1） 现随机转动转盘一次，停止后，指针指向1的概率为______；

（2） 小明和小华利用这个转盘做游戏，若采用如图5的游戏规则，你认为对双方公平吗？请用列表或画树状图的方法说明理由.

【分析】（1） 随机转动转盘一次，停止后，三个等可能的情况中出现1的情况有一种，故指针指向1的概率为；

（2） 列表得：

所有等可能的情况有9种，其中两数之积为偶数的情况有5种，两数之积为奇数的情况有4种，

∴P（小明获胜）=，P（小华获胜）=，

∵>，∴该游戏不公平.

【点评】此题考查了游戏公平性，以及列表法与画树状图法，判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平.

例4 （2014·江苏连云港）如图6，在一个不透明的袋子中装有四个球，分别标有字母A、B、C、D，这些球除了字母外完全相同，此外，有一面白色、另一面黑色、大小相同的四张正方形卡片，每张卡片两面的字母相同，分别标有字母A、B、C、D. 最初，摆成如图7的样子，A、D是黑色，B、C是白色.

两次操作后观察卡片的颜色.

（如：第一次取出A、第二次取出B，此时卡片的颜色变成 ）

（1） 求四张卡片变成相同颜色的概率；

（2） 求四张卡片变成两黑两白、并恰好形成各自颜色的矩形的概率.

【分析】（1） 画树状图得：

∵共有16种等可能的结果，四张卡片变成相同颜色的有4种情况，

∴四张卡片变成相同颜色的概率为；

（2） ∵四张卡片变成两黑两白，并恰好形成各自颜色矩形的有8种情况，

∴四张卡片变成两黑两白，并恰好形成各自颜色矩形的概率为：=.

【点评】本题考查的是用列表法或画树状图法求概率. 列表法或画树状图法可以不重复不遗漏地列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件. 用到的知识点为：概率=所求情况数与总情况数之比.

同学们，上面我们列举了本章内容的一些典型题目，这些题目多考查了统计和概率的一些简单应用，只要各位同学熟悉教材中的几个统计量，合理抽取样本，理解用样本估计总体的必要性，会建立合适的概率模型并进行简单的计算，一定能合理地解释生活中的一些概率问题，并能在中考中熟练地解决这些题目.

（作者单位：江苏省无锡市仓下中学）