分析信息作出决策

诸广平

同学们，学习本章知识时，你们有什么感受？可能你们会觉得本章和我们以往学过的大部分数学知识有些不同. 确实，在“概率和统计的简单应用”这一章里，既没有复杂的计算，也很少涉及严密的逻辑推理，还无需同学们发挥丰富的空间想象能力. 不过，本章要求同学们对提供的信息作出分析，甚至要求根据分析作出决策. 下面，我们就对本章出现的一些典型问题作一个回顾.

一、 关于简单随机抽样

例1 判断下列抽样调查选取样本的方法是否合适，并说明理由：

（1） 为了解某地区老年人的健康状况，在该地区医院里调查了100名老年病人1年内生病的次数；

（2） 某方便面厂家为了解产品质量情况，在生产线上每100包随机抽取1包进行检查；

（3） 为了解某城市的空气污染情况，调查了该城市某个月的空气污染情况.

这一题主要是考查同学们对简单随机抽样的理解. 一般来说，判断抽样调查是否合理，主要是看提取的样本是否具有代表性，以及总体中每个个体抽到的可能性是否相同. 本题中，第（1）小题调查的是该地区全体老年人的健康状况，但是选取的样本却是医院里的病人，根本不能代表所有的老年人，因此不具有代表性. 同样第（3）小题只选取了某一个月的空气污染情况，也不具有代表性，如果在每个月里随机抽取若干天，会更合理. 只有（2）是合适的.

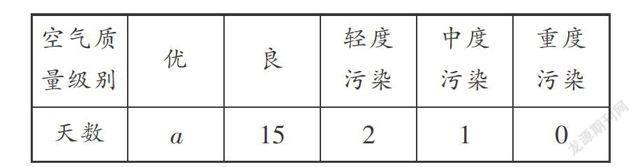
例2 （2010·福建厦门）小明学完了统计知识后，从“中国环境保护网”上查询到他所居住城市2009年全年的空气质量级别资料，用简单随机抽样的方法选取30天，列出下表：

请你根据以上信息解答下面问题：

（1） 这次抽样中“空气质量不低于良”的频率为______；

（2） 根据这次抽样的结果，请你估计2009年全年（共365天）空气质量为优的天数是多少？

本题主要考查抽样调查的作用：用部分估计总体，也就是用样本的统计量来估计总体的统计量.

（1） 根据频率等于频数与总数的商，可以算得，这次抽样中，“空气质量不低于良”的频数是30-0-1-2=27，因此频率为=0.9；

（2） 因为样本中空气质量为优的天数a=30-（15+2+1）=12，频率为0.4，因此估计总体（也就是全年的空气质量情况）中空气质量为优的频率也是0.4左右，所以估计全年空气质量为优的天数为365×0.4=146（天）.

二、 利用统计分析作预测

例3 随机调查了某校10名九年级男生的身高和体重，整理如下：

（1） 以体重为横坐标，身高为纵坐标，在平面直角坐标系中画出相应的点，并选用一条适当的直线近似表示该校九年级男生身高与体重之间的关系；

（2） 求这10名男生身高与体重之间数量关系的近似表达式，并由该表达式估计该校身高为180 cm的九年级男生的平均体重.

在平面直角坐标系中描好这10个点以后，同学们会发现，这些点大致分布在一条直线附近，为此我们可以选取其中两个点，求出经过这两个点的直线表达式，就用这条直线表达式来近似地表示该校九年级男生身高与体重之间的关系（显然，同学们可能会选取不同的两个点，从而求出的直线表达式也会不同，不过没有关系哦，因为同学们会发现这些不同的直线差距很小，况且我们这里是用来近似表示两者之间的关系）. 比如，我们选取（49，170），（69，183）两点，则可求得y=0.65x+138.15. 从而第（2）小题中，当身高为180 cm时，可求得平均体重为64.4 kg.

三、 利用概率判断是否公平

例4 一个不透明的袋子中装着标号为1，2，3，4的4个小球，这些球除颜色外都相同. 甲乙两人共同协商了一个游戏规则：将球搅匀后，每人从中摸出一个球，其中摸出的球上的标号大的一方获胜.

（1） 若甲先摸球且摸出的球不放回，乙再摸球，求乙获胜的概率；

（2） 若甲摸出的球放回后乙再摸球，此时制订的游戏规则公平吗？为什么？

第（1）小题中，要求乙获胜的概率，相信同学们应该能轻松解决，对了，通过列表或者画树状图的方法，列出所有可能的情况共12种，其中乙胜的情况数为6种，因此乙获胜的概率为0.5；关于第（2）小题，要判断游戏规则是否公平，同学们想想看，应该根据什么来判断呢？不错，就是看在该规则下甲乙两人获胜的概率是否相同！因此，只需算出甲乙两人的获胜概率，就可以作出判断. 同样列出表格或者树状图，可以看到，现在的所有可能的情况是16种了，不过其中有四种是平局，另外甲胜有6种，乙胜也有6种，因此甲乙两人获胜的概率都是0.375，因此这个游戏规则是公平的.

同学们，这一类问题的解决方法应该清楚了吧？不妨再挑战难度大点的：如果把游戏规则改为甲先摸球，记下标号后放回，然后乙再摸球，把两人摸到的球的标号相加，如果和为偶数，则甲胜，否则乙胜. 请问这个游戏规则公平吗？

相信同学们应该能解决，万变不离其宗，仍然是分别求出两人获胜的概率，看看是否相同，相同则规则是公平的，否则就是不公平哦！

例5 （2014·云南）某市“艺术节”期间，小明、小亮都想去观看茶艺表演，但是只有一张茶艺表演门票，他们决定采用抽卡片的办法确定谁去，规定如下：将正面分别标有数字1、2、3、4的四张卡片（除数字外其余都相同）洗匀后，背面朝上放置在桌面上，随机抽出一张记下数字后放回，重新洗匀后背面朝上放置在桌面上，再随机抽出一张记下数字. 如果两个数字的和为奇数，则小明去；如果两个数字的和为偶数，则小亮去.

（1） 请用列表或画树形图（树状图）的方法表示抽出的两张卡片上的数字和的所有可能出现的结果；

（2） 你认为这个规则公平吗？请说明理由.

怎么样？有信心解决这个问题吗？再次强调一下，要根据概率来判断游戏规则是否公平哦！

四、 利用概率进行估计

例6 为了估计鱼塘中鱼的数量，先从鱼塘中捕捞30条鱼做上标记，然后放回鱼塘，经过一段时间，待有标记的鱼完全混合于鱼群后，再从中多次捕捞，并算得每200条鱼中，带有标记的鱼有5条，试估计该鱼塘中鱼的数量.

根据什么来估计鱼塘中鱼的数量呢？肯定与有标记的鱼出现的频率有关. 因为这个频率可以作为有标记的鱼出现的概率的估计值. 因此，可以估计带有标记的鱼出现的概率是0.025，而总共有30条鱼带有标记，于是估计鱼塘中鱼的总数为30÷0.025=1 200（条）.

例7 （2014·福建莆田）某校为了解该校九年级学生对篮球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况，对九年级部分学生进行了随机抽样调查，每名学生必须且只能选择最喜爱的一项运动项目，将调查结果统计后绘制成如下两幅不完整的统计图. 请根据图中的信息，回答下列问题：

（1） 这次被抽查的学生有______人；请补全条形统计图；

（2） 在统计图2中，“乒乓球”对应的扇形的圆心角是______度；

（3） 若该校九年级共有480名学生，估计该校九年级最喜欢足球的学生约有______人.

仔细读统计图表，同学们肯定能发现，喜欢羽毛球的同学共有9人，占15%，因此被抽查的学生共有60人，于是你能算出这次调查中喜欢足球的学生有多少人了吗？对了，有6人. 那么这次调查中喜欢足球的频率就是0.1，于是估计喜欢足球的概率也是0.1左右，到这里，相信同学们已经可以轻松估计出该校九年级最喜欢足球的学生约有多少人了.

五、 根据概率计算该如何收费

例8 某航空公司的保险合同上有这样一个条款：飞机一旦失事，公司将向每名乘客赔偿人民币50万元，但保险公司需向每名乘客收取保险费20元. 如果该航空公司航班平均每次约有120名乘客，那么在n次飞行中，平均来说，当飞机失事的概率不超过多少时，才能保证保险公司的收入不小于支出？

本题要求公司的收入不小于支出，这是一个不等关系，我们需要把这个不等关系转化为关于飞机失事概率P的不等式，从而求出P的范围. 在n次飞行中，保险公司共收取费用120×20n元，平均失事nP次，平均赔偿500 000×120nP元. 同学们，这些数量关系能理清吗？于是得到不等式120×20n≥500 000×120nP，解得P≤0.000 04.

同学们，上面我们对本章出现的一些经典问题进行了回顾与总结、拓展与延伸，相信同学们对本章知识一定有了更深的体会，也有了更大的收获.

（作者单位：江苏省无锡市张泾中学）