高等数学试卷质量定量评价模型及分析

刘洪霞 周绍伟

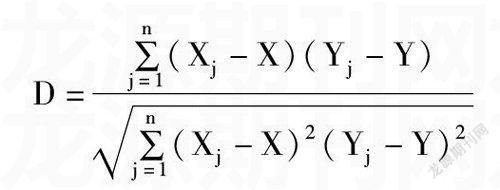
评定教学质量的主要依据是学生成绩的分布，而影响学生成绩的客观因素又是试题本身的质量，因此提高试卷质量是教学工作中的一个关键[2]。高等数学是理工科院校的一门重要基础课，对学生后继课程的学习起着至关重要的作用。为了提高高等数学的教学质量，我校高等数学一直遵循教考分离、全校统考的原则。这就对命题老师提出了很高的要求，一套高质量的试题能准确地反映学生学习的真实水平。本文对我校2014—2015学年的高等数学上册期末考试进行定量评定并根据学生的考试成绩进行分析。

一、试题质量分析

本次分析的试卷的使用对象为大学工科专业一年级本科学生。本次试卷命题的内容为高等数学上册的全部内容，主要知识点为一元函数的微积分及其应用和常微分方程，满分100分。试题覆盖面广，内容分布均匀，命题形式丰富，命题形式为：填空题、选择题、计算题、解答题和证明题。

命题分值的分布如下：

表1

二、试卷质量评价

1.试题难度

试题难度是指试卷的难易程度，是评价试题质量好坏的重要指标。下面根据题型的种类对每种题型的难度进行量化评价。

（1）客观题难度計算公式：P■=1-■

其中P■为难度系数，R为答对该题的人数，N为参加考试的总人数。

（2）主观题难度计算公式：P■=1-■

其中P■为难度系数，R为被测试学生的平均得分，X为该题的满分。

在我校参加统考的一年级学生中随机抽取10个自然班级，共386个学生的试卷，对试题进行评价，结论见表1。

表1    试题难度系数及评价

一般来说难度系数为0.5说明难易程度适中，难度系数小于0.3我们认为试题过于简单，难度系数大于0.7则说明试题较难。从统计结果看该试题的难易程度适中。

2.试题区分度

试题区分度是指试题对于不同水平的学生加以区分的量度。通过测试，学习成绩好的学生得分高，学习成绩差的学生得分低，则说明试题的区分度较好。反之，各个层次的学生得分差别不大则说明试题的区分度较差。

（1）客观题区分度采用两端分组法

将学生的考试成绩进行排序，选出得分较高的27%为高分组，得分较低的27%为低分组，把高分组和低分组答对该题的比例以百分比记为P■和P■，则区分度P=P■-P■。

（2）主观题区分度的计算公式为

其中X■为测试所得总分，Y■为该题得分，X，Y为对应的平均分，n为被测试的人数。

结论见表2。

表2    试题区分度及结论

三、试卷成绩分析

在我校参加统考的一年级学生中随机抽取10个班级，386个学生的成绩对试卷进行统计，使用SPSS软件对学生考试成绩进行评定，结论见表3和表4。

表3    学生成绩区间分布

图1    学生成绩区间分布

表4    统计量描述

四、题目分析

试卷中有一道综合题，如下：

设抛物线y=ax■+bx+c通过点（0，0），且当x∈[0，1]时，y≥0，试确定a，b，c的值，使得抛物线y=ax■+bx+c与直线x=1，y=0所围图形的面积为■，且使该图形绕x轴旋转而成的旋转体的体积最小。

解：抛物线y=ax■+bx+c与直线x=1，y=0所围图形的面积可表示为：

A=？蘩■■（ax■+bx）dx=■+■

所围图形绕轴旋转而成的旋转体的体积：

V=？蘩■■π（ax■+bx）■dx=π（■+■+■）

由A=■得a=■-■，代入V中得：V=■（b-2）■+■π

由上式可知，当b=2时，旋转体的体积V最小，所以当a=-■，b=2时满足题意。

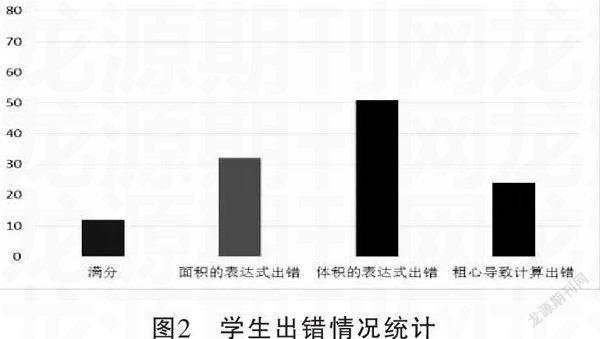
该题属于定积分应用的综合题目，考察的知识点是平面面积的计算和旋转体体积的计算，以及如何求函数的最值。满分为10分，抽取两个自然班82分试卷进行统计，总结学生出错主要集中在三个方面，一是面积的表达式出错，二是旋转体的体积的表达式出错，三是粗心计算出错，统计结果见图2。

图2    学生出错情况统计

从统计结果看，该题的失分率较高，满分同学较少。平面图形的面积掌握得较好，但是旋转体体积的计算掌握情况不好。另外，部分同学计算失误较多，说明平时做题较少，老师在上课过程中还要加强这方面的训练。

此外，抽取两个自然班，82份试卷，对试卷按题型进行分类，对得分率进行统计。

表2    试题区分度及结论

从统计结果可以看出，计算题的得分率要比解答题、证明题都要高，这说明学生学习受中学学习数学习惯的影响较大，仅掌握结题方法;证明题的得分率最低，这说明学生对知识的理解还不够透彻，还需要教师在课堂教学中有针对性地加以训练。

四、结语

本文针对影响试题质量的关键因素，对试题的难度、区分度建立了定量评价模型。依据这些评价模型，对高等数学试卷进行了客观准确的评价。从试卷评定模型和学生成绩两方面看，该试卷质量较高，学生学习成绩良好，但试卷中反映的问题还需要老师在以后的教学中加以强调。试卷评价和学生成绩分析，一方面可提高试题质量，改进考试设计工作，另一方面可促进教学质量的提高。

参考文献：

[1]倪锦君.用spss对试卷成绩进行统计分析[J].科技咨询，2010（3）：224-225.

[2]葛涛，吴建明，尤春风.试题质量定量评价模型[J].河北理工学院学报，2003（4）：120-122.

[3]李敏，补爱军.Mathematica在二重积分教学中的应用[J].怀化学院学报，2013（5）：82-84.

[4]林治.试卷评价与试卷质量的分析研究[J].扬州教育学院学报，2006（9）：89-91.

本文山东科技大学教育教学研究“群星计划”项目（qx2013265）和山东科技大学教学研究项目JG201504资助。