利用SPSS实现命题质量的定量分析
2015-09-10赖翔晖张华
赖翔晖 张华

摘 要: 考试是评价教育效果的重要手段,而命制试题则是考试中的重要一环。过去,对试卷命题的质量评价常以主观定性的方式为主。现在可以依靠SPSS(统计产品与服务解决方案)软件,实现对命题质量的定量分析。
关键词: 命题质量 定量分析 质量评价
一、命题定量分析的准备工作
启动SPSS19.0中文版,选择“变量视图”中,在名称下输入学号、题目1—12、总分等命题基本情况项目。在类型标记中,将学号定义为名义,将题目1—12定义为度量,小数根据实际情况设定,其他项保留默认设置。选择“数据视图”标签,在各行内输入学生的各题得分和总分数据(图2)。
图1 定义变量设定图
图2 数据输入图
二、命题的定量分析
(一)描述性统计量分析
用以描述考试总体情况的各分数统称为描述性统计量。在SPSS中,点击“分析—描述分析—频率”。将“总分”等变量名称选入待计算变量框中,在“统计”中选择要计算的统计量,选中均值、极值、标准差、中位数等项,最后输出结果(表3)。
表3 有效数据的得分描述性统计
(二)试题的正态分布预期
在學生群体足够大时,学生的能力呈正态分布。处于能力尖端和尾端的学生数量少,处于能力中端的学生数量多。在考试命题适宜,教学状况正常,学生水平相当,试卷评阅严谨的前提下,一份合格的试题,所反映出的学生成绩应呈现正态分布的特点。为研究试题能否体现学生能力的正态分布,可在SPSS软件中点击“分析—描述分析—频率”,在“频率”对话框中选择“图表”,点选绘制“总分”的直方图并标变化曲线(图4)。
图4 学生总分的直方—变化曲线图
若学生总分的直方—变化曲线图能呈现正态分布,那么,可进一步探究命制试题的正态分布预期。可利用单个样本K-S校验测查给定数据与正态分布间的显著差异。在SPSS中,点击“分析—非参数检验”,对“总分”进行单个样本K-S检验(表5)。
表5 试题总分的单样本Kolmogorov-Smirnov检验
(三)难度
试题的难度(P)是测验题目难易程度的统计量。试卷难度等于试卷内各题的平均难度。要观测命题试卷难度,应先测量命题试卷内各题难度。试题计分方法不同,难度计算方法不同。
二分法计分(选择题、判断题)题目的难度统计。对于二分法计分的题目,答案只有对与错两种可能的结果(即答对得分,答错不得分)。此类题目难度通常用通过率(P)表示。其中,P=1—R/N(其中R为答对该题的人数,N为答题总人数)。由此,可在SPSS中,运用“转换—计算变量”方法,在“计算变量”对话框中输入公式,直接算出二分法题目难度(表6)。
表6 二分法计分题目难度值
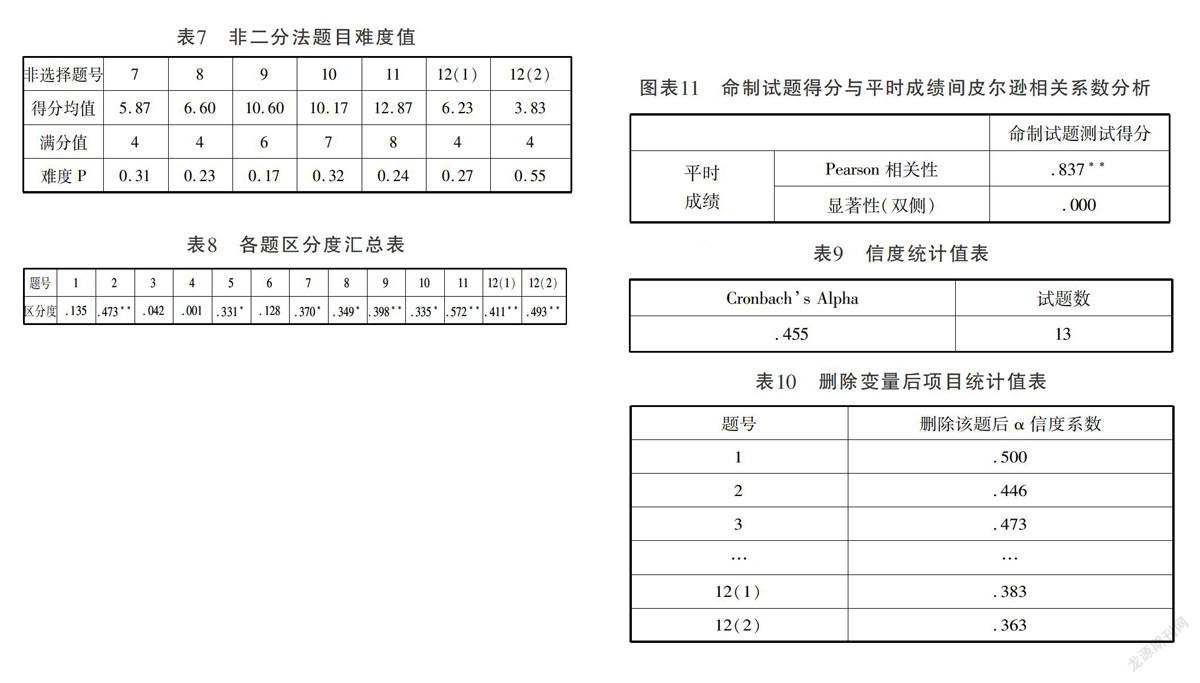
非二分法计分(主观题、论述题)题目的难度统计。对于非二分法计分的题目,难度(P)可以通过公式P=1—X/W(X为该题目均分值,W为该题满分值)计算。可采用“计算变量”方法直接输入公式,算出非二分法题目难度(表7)。
表7 非二分法题目难度值
全卷难度值(P)等于卷内各题难度平均值,采用SPSS“计算变量”可得p=0.4。
(四)区分度
区分度是反映试题区别学生水平和能力的统计量。在实际统计时,常以考试总分作为考生的实际水平,而把某题的得分与学生总分之间的相关系数作为该题的区分度。
客观题的区分度统计,可把客观题得分视为等间距测度的连续变量,采用Spearman等级相关分析统计区分度。主观题的区分度统计,可把主观题成绩视为非等间距测度的连续变量,采用Pearson相关分析。在SPSS中,点击“分析—相关—双相关”。先选择客观题各题分数和总分采用Pearson相关分析(1-6),再选择主观题(7-12(2))各题分数和总分采用Spearman相关系数分析,得到结果合成(表8)。
表8 各题区分度汇总表
(五)信度
信度是衡量一次考试可靠性、稳定性的统计量。信度代表着试题的可靠性,其取值在0至1之间。信度越高,可靠性越好,但容易造成成绩标准差过大。一般采用SPSS中克伦巴赫系数(Alpha模型)计算命题试卷一致性信度系数。在SPSS中,点击“分析—度量—可靠性分析”。在可靠性分析对话框中,选择试卷各题得分数据。点击“统计量”,选择“如果项已删除则进行度量”,结果如下(表9-10):
表9 信度统计值表
表10 删除变量后项目统计值表
(六)效度
效度是指测试结果的准确性与有效性程度的统计量,即一个测验能够测量学生水平的程度[2]。可采用效标效度法测量试题的效度。将学生的平时成绩作为效度分析的校标,利用皮尔森相关系数法计算命题测试分数与校标之间的相关系数,结果即为试题效度(表11)。
图表11 命制试题得分与平时成绩间皮尔逊相关系数分析
三、命题质量评价
第一,描述性统计量分析。由表3可知,命题平均成绩为32.54分(满分49分),最高分45分,最低分12分,标准差为6.94。平均分、标准差数值适当,极值差距较大,体现了学生个体之间对题目的理解差异大。由此可见,试卷命题中,部分题目可能表意不清,引发部分学生无从下手作答的情况。此卷应注意题干的表达,使学生清晰了解题目意图。
第二,正态分布预期分析。由图4可知,学生总分变化曲线呈正态分布曲线样式,因而命制试题具有正态分布预期。由表5进一步分析K-S检验中的各数值可知,Z值为0.493,sig(双侧P值)=0.851>0.05,由sig(渐进显著性)>0.05,可得给定数据与正态分布没有显著性差异,即总分数据符合正态分布要求。
第二,试题难度分析。一般认为,命题难度在0.4至0.7之间为宜,难度值小于0.4的题目难度较小,难度值大于0.7的题目较大。一般认为,最好的试题难度应接近于中等难度(即p=0.5)。因此,本命制试题全试卷具有中等偏下的难度(p=0.4)。这份命制试题如果运用在终结性考核中,用以检测学生在群体中知识掌握水平,作为合格水平测验,则效果较好。但作为过程性考核,则其难度水平较低,需适当加大难度。由表6、7可知,T9、T1难度过小,建议予以删改。T6、T3难度过大,应进一步结合课程评价标准加以研究,检验是否超纲。
第三,区分度分析。一般认为区分度在0.4以上的题目,鉴别能力优秀;区分度在0.3至0.39间的题目,鉴别能力良好;区分度在0.39以下的题目,应进行删改。由表8可知,全卷区分度总体水平适宜,能够区分学生掌握知识程度的优劣。但T1、T3、T4、T6四题区分度较低(<0.39),说明学生在作答这些题目时,掌握的知识和对知识理解、运用的能力不能充分体现在试卷答题分数上,因此,应作删改。
第四,信度分析。从表9可知,本次考试的信度为0.455。普遍而言,学校测验采用试卷信度应达到0.5以上。本命题试卷达不到可信要求,为提高本卷信度,本卷应进行修改。从表10可知,删除T1后全卷信度提升至5.0,故可考虑对T1进行替换。同时,目前本卷题量共12题,题目数量较少,可考虑通过适当增加题量的方法,提高全卷信度。
第五,效度分析。从表11可知,全卷效度值为0.837,在0.01的显著性水平下,sig.值(显著性)为0.000,表明学生完成命制试题的得分与学生平时的成绩两者间呈显著的相关关系。命制试题具有较高的效度。
参考文献:
[1]张雪冰.试卷分析中的正态分布和非正态分布[J].安徽建筑工程学院学报(自然科学版),2009.8(17-4).
[2]陈伙平.教育科学研究方法与原理[M].福建科学技术出版社,2005.7,124.
