天体运动中的加速度与向心加速度的区别与联系

李华

摘 要： 比较卫星在椭圆轨道与圆轨道的切点处的加速度大小或者向心加速度的大小，是关于天体运动这一知识点的高频考点，而卫星的加速度和卫星的向心加速度又是一对容易混淆的概念，二者之间有什么区别，又有哪些联系呢？本文对此进行讨论。

关键词： 加速度 向心加速度 近地点 远地点 天体运动

比较卫星在椭圆轨道与圆轨道的切点处的加速度大小或者向心加速度的大小，是关于天体运动习题中的高频考点，而卫星的加速度和卫星的向心加速度又是一对容易混淆的概念，二者之间有什么区别，又有哪些联系呢？下面对此进行讨论。

一、加速度和向心加速度有什么不同？

首先，物理意义不同：加速度是描述物体运动速度变化快慢的物理量。向心加速度是反映物体运动速度方向变化快慢的物理量。

其次，一般情况下的计算方法不同：加速度大小的求解通常是依据牛顿第二定律进行求解，a=■即物体加速度的大小跟它受到的作用力成正比，跟它的质量成反比；向心加速度大小通常根据a■=■或者a■=■=ω■r进行求解。

那么加速度的大小和向心加速度的大小在什么情况下相等呢？

对于变速圆周运动，通常根据合外力产生的效果，可以把合外力F■分解为两个相互垂直的分力：跟圆周相切的分力F■和指向圆心的分力F■。其中跟圆周相切的分力F■产生切向加速度，改变速度大小；指向圆心的分力F■产生向心加速度，改变速度方向。

当切向加速度为0时，合外力全部用来提供向心力，F■=F■。由a=■与a■=■可知，加速度的大小和向心加速度的大小相等。

在天体运动中，哪些情况下加速度的大小和向心加速度的大小相等呢？

第一种情况：卫星在圆轨道上做匀速圆周运动时，速度大小不变，切向加速度为0，万有引力全部提供向心力，卫星的加速度大小等于向心加速度的大小。

第二种情况：卫星在椭圆轨道的近地点和远地点，万有引力方向与线速度垂直，切向加速度为0，万有引力全部提供向心力，卫星的加速度的大小等于向心加速度的大小。注意，在椭圆轨道上其他位置处，速度大小变化，切向加速度不为0，万有引力的一个分力提供向心力，卫星的加速度的大小和向心加速度的大小不相等。

二、通过两道例题体会如何比较不同轨道上加速度的大小或者向心加速度的大小。

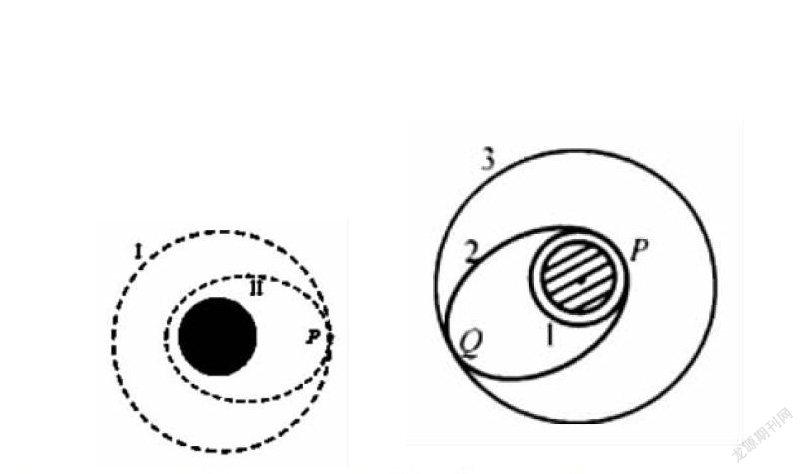
例题1：我国发射了一颗地球资源探测卫星，发射时先将卫星发射至距离地面50km的近地圆轨道1上，然后变轨到近地点距离地面50km、远地点距离地面1500km的椭圆轨道2上，最后由轨道2进入半径为7900km的圆轨道3。如下图所示，轨道1、2相切于P点，轨道2、3相切于Q点。忽略空气阻力和卫星质量的变化，以下说法正确的是（ ）

A.该卫星从轨道1变轨到轨道2需要在P处点火加速

B.该卫星在轨道2上稳定运行时，P点的速度小于Q点的速度

C.该卫星在轨道2上Q点的加速度大于在轨道3上Q点的加速度

D.该卫星在轨道3的机械能小于在轨道1的机械能

答案：A

例题2：北京时间2013年12月10日晚上九点二十分，在太空飞行了九天的“嫦娥三号”飞船，再次成功变轨，从100km的环月圆轨道Ⅰ，降低到近月点15km、远月点100km的椭圆轨道Ⅱ，两轨道相交于点P，如下图所示。关于“嫦娥三号”飞船，以下说法不正确的是（ ）

A.在轨道Ⅰ上运动到P点的速度比在轨道Ⅱ上运动到P点的速度大

B.在轨道Ⅰ上P点的向心加速度比在轨道Ⅱ上运动到P点的向心加速度小

C.在轨道Ⅰ上的势能与动能之和比在轨道Ⅱ上的势能与动能之和大

D.在轨道Ⅰ上运动的周期大于在轨道Ⅱ上运动的周期

答案：B

其中，例题1中的C选项和例题2中的B选项，都是对于卫星在圆形轨道和椭圆形轨道切点处的考察；不同之处在于前者考察的是加速度，后者考察的是向心加速度。

对于例题1中的C选项，可以利用牛顿第二定律直接求解，即G■=ma。无论在哪个轨道上，都有Q点到地心的距离r相等，万有引力的大小相等，合外力的大小相等，因此加速度的大小相等，C选项错误。

对于例题2中的B选项，因为在I轨道上经过P点的线速度大小大于在II轨道上经过P点的线速度大小，在I轨道上的半径大于在Ⅱ轨道的曲率半径，所以无法利用a■=■求解。由前面的讨论可以得知，卫星在I轨道上做匀速圆周运动时，卫星的加速度大小等于向心加速度的大小；卫星在Ⅱ轨道经过P点时，卫星的加速度的大小等于向心加速度的大小。I轨道、Ⅱ轨道经过P点时加速度的大小相等，因此向心加速度的大小也相等，B选项错误。