江苏省专转本考试高等数学辅导策略研究

摘 要： 通过对江苏省十五年专转本高等数学考试真题的大数据分析，作者总结了专转本高等数学辅导策略，归纳了一些行之有效的方法，包括： 吃透大纲，明确方向；了解学生，因材施教；钻研真题，有的放矢；方法灵活，事半功倍；知识串讲，专题研究；现场模拟，查漏补缺；课内讲授，课外答疑，一步一步深入考题，最终获得高分取胜。

关键词： 大数据 专转本 高等数学

自从2001年开始，江苏省开始实施专转本统一考试，民间称之为“第二次高考”，很多高职学生通过统一考试，考上了本科。这几年，招生院校中增加了一些公办二本院校，报考学生热情高涨，招生院校精挑细选，竞争日趋激烈。理工类考生在考试时，高等数学是必考的三门课程之一，总分150分。另外，英语总分150分，计算机基础总分100分。高等数学这门课知识点多，覆盖面广，计算量大，题目灵活，全面考查了学生的计算能力、逻辑推理能力、空间想象能力。而且高数在总分中所占比重较大，区分度也高，很多学生比较畏惧。笔者长期从事专转本辅导班的授课，结合多年授课经验，统计分析了十五年考试真题的大数据。现将辅导策略总结如下。

1.吃透大纲，明确方向

教师要组织学生利用业余时间学习《专转本高等数学考试大纲》。大纲是备考的一盏明灯，为备考指明了方向。教师紧扣大纲，准确把握考试内容和考试要求。授课过程中，避免偏题怪题，切实把握好授课的广度和深度。

2.了解学生，因材施教

教师要充分了解辅导班学生情况，了解学生所学专业、数学基础、准备报考院校和专业等情况。以南京工业职业学院学生为例，经济管理学院和计算机与软件学院学生一般只学了一元微积分知识，机械工程学院和能源与动力学院学生基本学习了专转本考试要求的内容。从录取方式上看，有些是职业高中对口单招来的，有些是高考提前自主招生来的，有些是通过高考统招录取的，高考统招录取的学生中，根据高考分数，有的录取到国际教育学院，有些录取到海外本科直通车班，这几类学生基础较差，只有高考统招普通班学生基础要好些。掌握了这些情况后，考虑到学生差异，教师要灵活制订授课计划，适当调整授课内容，真正做到因材施教，确保学生考试取得优异成绩。

3.钻研真题，有的放矢

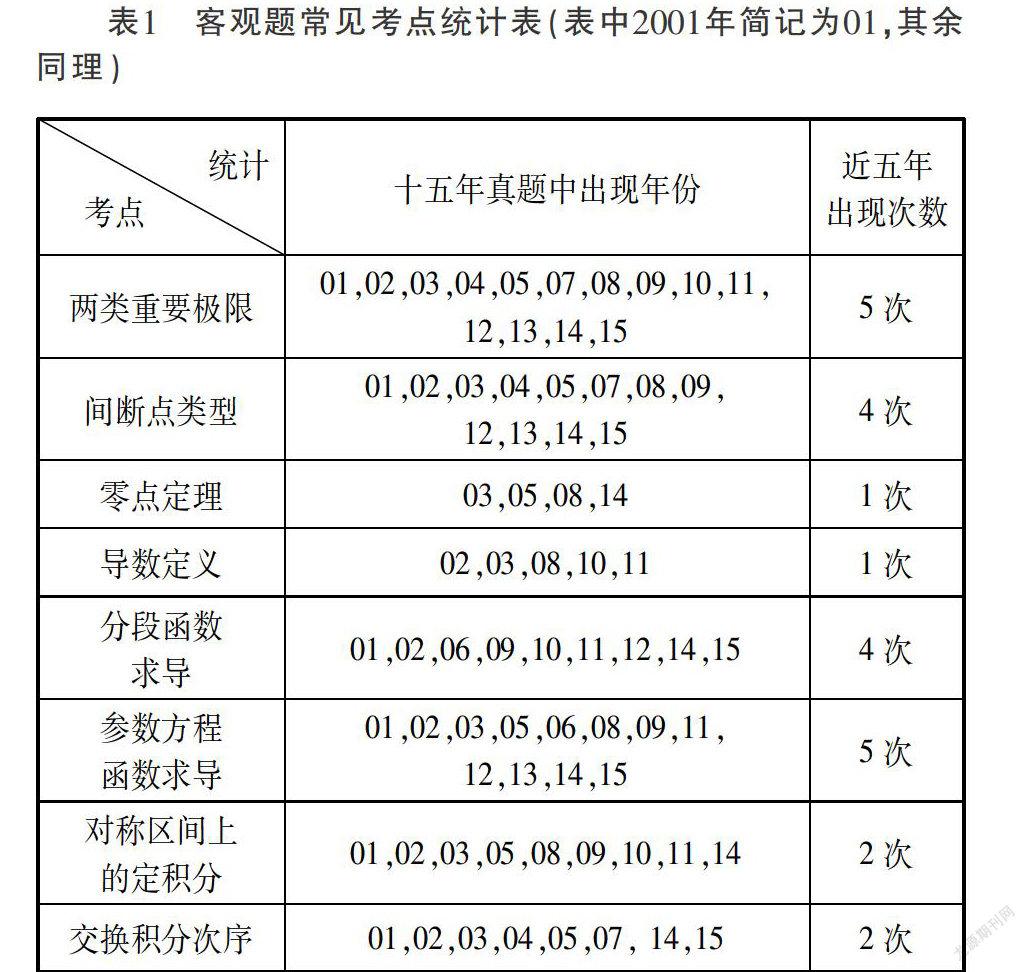
到目前为止，专转本考试共举行了十五次，教师要认真钻研十五年的考试真题，了解考试题型，搞清知识点的分布与分值，准确把握考试重难点，统计学生的主要丢分题目，预测出题方向，这样备考工作就会做到有的放矢，成竹在胸。尽管高数试题题量较大，试题灵活，但是仍然以基本知识、基本技能为考查重点。考查内容主要是极限、微分学、积分学三大块。其中一元函数的极限、微分学、积分学占总分的70%左右。题型分为主观题和客观题，总共24道题。选择题6题共24分，总分占比16%，填空题6题共24分，总分占比16%，计算题8题共64分，总分占比43%，综合题2题20分，总分占比13%，证明题2题共18分，总分占比12%。根据十五年的大数据统计，以主观题中的8道计算题为例，第13题一般是极限题，第14题一般是参数方程所确定的函数的导数，第15题一般是不定积分题，第16题一般是定积分题，第17题一般是平面方程或者直线方程题，第18题一般是关于二元抽象函数的二阶偏导，第19题一般是二重积分题，第20题一般关于是二阶微分方程的求解 。明显看出，计算题考点已经固化，大概高等数学每一章考一道计算题，无非有时候顺序变动一下。同样，通过对大数据的统计分析，发现综合题和证明题的考点也是如此，像定积分的几何应用，不等式的证明，分段函数的求导也几乎是每年必考的内容。牢牢掌握了主观题的考点后，就等于抓住了复习的重点。但是“抓大”的同时也要“抓小”，这样才能将知识点一网打尽，考出高分。通过对大数据的统计分析，客观题常见考点出现情况如表1所示。

由表1可以看出，两类重要极限和参数方程所确定的函数的求导是每年必考的题目，间断点的类型判断也是常考考点，这些内容在授课中必须讲解透彻，人人熟练掌握，确保万无一失。由于篇幅所限，其他必考常考考点不再一一列出。教师透彻钻研历年考试真题，进行大数据统计分析，才能对考试重难点了如指掌，对必考常考考点心中有数，在此基础上，甚至可以对来年考题进行预测，授课做到有的放矢，直奔重难点。复习充分，学生考试获得高分也是顺理成章、水到渠成的事。

4.方法灵活，事半功倍

整个高等数学内容丰富，知识点多，有些内容部分同学根本没有学过，有些同学数学一直是一个薄弱环节，有些同学数学基础相对较差。生源的多样性要求作为辅导班授课教师必须采用灵活高效的授课方法。笔者一般采用主线教学法、类比教学法、模型教学法、一题多变法。高等数学以函数为研究对象，极限是主要研究方法。它的主线是函数→极限→连续→微分学及其应用→积分学及其应用→无穷级数→向量代数与空间解析几何。沿着课程主线，内容从前往后，循序渐进，环环相扣，层层展开。主线教学法教会学生“解剖”数学，清晰把握知识脉络，构建横向、纵向、网状的知识网络，对整个内容立体框架了然于胸。类比教学法将具有相似结构和特点的知识点进行表格罗列，这样形成了鲜明而强烈的对比，一方面掌握概念的主要内容，另一方面搞清楚它们之间的联系和区别，记忆深刻，不易混淆[1]。如向量的点乘与叉乘类比，定积分与二重积分类比，平面与直线类比等。平面与直线的类比如表2所示。

利用模型教学法，学习导数想到曲线斜率，学习定积分想到曲面面积，学习二重积分想到柱体体积，这样抽象的内容就变得形象生动，不再枯燥无味。针对具体题目，采用“一题多变法”，将题目进行类比、延伸、拓展，可以将相关知识点联系起来，提高学生综合分析和应用能力。采用上述方法，灵活组织教学，可以有效增强教学效果，起到事半功倍的作用。

5.知识串讲，专题研究

第一阶段分章节从前往后讲解完后，进入第二阶段：知识串讲和专题研究。极限是高等数学的研究方法，是贯穿高等数学的一条看不见的线索，高等数学中的主要内容，如函数的连续性、导数、定积分、二重积分、广义积分的收敛性、无穷级数的收敛性和收敛半径的计算等等，都与极限密切相关[2]。可以借助极限，将这些内容串讲。专题研究中，可以介绍各种求极限的方法，裂项法的应用，变上限积分函数的综述，如何构造辅助函数等。这两种方法将分散的内容集中起来，将知识点前后联系，融会贯通，进一步提高了学生的解题能力。

6.现场模拟，查漏补缺

第三阶段以现场模拟为主，通过模拟专转本考试，发现各种问题。有些是计算能力要增强，有些是公式不熟悉，有些是粗心大意，有些是存在知识盲点，有些是综合分析应用能力较弱，有些是证明题无从下手。通过模拟，每个学生查漏补缺，及时发现问题，力争在考试之前有针对性地解决这些问题。

7.课内讲授，课外答疑

除了课内高效认真地组织授课外，教师还应该充分利用课外时间给学生答疑，最好是当面答疑。还应该编写《专转本高等数学复习指导》，利用飞信、QQ、微信、公共邮箱等及时解决同学们存在的问题。条件允许，还可以录制一些小视频，采用微课的形式给学生进行业余辅导。

专转本辅导是一个很重要的过程，对于学生能否实现本科梦至关重要，需要师生良好互动，共同努力。除了学习以外，教师还要积极帮助学生，科学引导他们，热情鼓励他们。同学们要紧跟教师节奏，发现问题及时解决，多做练习，善于归纳总结，互相交流，共同提高。

参考文献：

[1]彭红军，梁艳.概率论与数理统计课程的全程类比教学研究[J].数学教育学报，2012，2.

[2]高崚嶒.高职院校高等数学中极限教学的策略[J].高等函授学报，2011，6：52-54.

[3]浦志勤，于正，朱群生.高等数学同步辅导及全真模拟试题精解[M].西安：陕西师范大学出版社，2005.