寒温带兴安落叶松林生物量模型

都本绪

（大连市林业调查规划院，辽宁 大连 116023）

因地球大气中CO2等温室气体浓度的剧增而导致的全球气候变化以及由此产生的一系列生态环境问题已成为生态系统研究的焦点．而森林作为陆地生态系统的主体，在全球环境变化中起着举足轻重的作用。无论从其面积、生物量，还是碳储量上来看，森林都是地球生物圈的重要组成成分，是陆地生态系统的主体，在整个陆地生态系统的结构和功能中居于重要地位。对森林生物量，G.P Sparling于1986年首先探讨了兴安落叶松（Larix Kaempferi）的生物量估算模型[1]，ChenY.H（1998）阐述了光照对西部落叶松（Larix occidentalis）生物量的影响[2]，同年，Hillevi.M研究了西伯利亚落叶松（Larix sibirica）生物量在瑞典的分布规律[3]，H.Jiang（2004）做了收割对兴安落叶松（Larix gmelini）生物量的干扰研究[4]，G.S Zhou（2005）报道了落叶松蓄积量和生物量的关系[5]；国内对落叶松林（Larix）生物量的研究也有很大进展，程云屑等对我国不同地区兴安落叶松的生物量和生产力做了比较[6]，陈林娜等对华北落叶松（Larix principis-rupprechtii）的生物量进行了建模[7]，王喜武等对长白落叶松（Larix olgensis）的生物量分布也进行了探讨[8]；对于国内引种的兴安落叶松，王永祥（1999）探讨了辽宁地区生物量及其器官分配规律[9]，刘兴良在2003年以川西高峡谷地的生物量和生产力为对象做了研究[10]。

对于东北地区的兴安落叶松生物量，于立忠（2007）曾探索了辽宁地区兴安落叶松细根的生物量分布[11]。但前期研究中样地设置少而集中[12]。且前期的研究中尚未见有关兴安落叶松林地下生物量和林下灌草生物量的研究。而本文将以寒温带区兴安落叶松林生物量为研究对象进行建模和全面估算，以填补该地区该领域的空白。

1 研究区域和样地调查方法

兴安落叶松林主要分布于我国大小兴安岭地区（43～53.7N，118～132.5E），该地区属于寒温带季风气候区，冬季（候平均气温<10℃）长达9个月，夏季（候平均气温≥22℃）最长不超过1个月，绝大部分地区几乎无夏。年均气温4.7～54℃，无霜期长达90～180d，年均降雨量300～600mm，日温持续≥10℃的时期（生长季）自5月上旬开始，8月末结束，长70～100d，土壤为漂灰土，土层较浅薄，一般厚20～40cm，这一地区分布最广、面积最大的植被类型是杜鹃一兴安落叶松林，其乔木层多为兴安落叶松纯林，少数混生有白桦和樟子松，郁闭度0.4～0.9；灌木层主要由兴安杜鹃组成，盖度可达50%以上。

60块试验标准地分别均匀布设在该地区，样地大小为 800m2，分别在 2005年 8～10 月、2006 年 8～10 月进行样地调查，记录大地坐标、海拔、坡向、坡度、坡位、经营活动、土壤厚度和质地。对胸径大于4cm的树木进行每木检尺，记录树种、胸径、树高（用Vertex IV超声波测高仪测定）、相对于测点的方位角和水平距离等指标。按径阶选定标准木伐倒，分根、干、皮、枝、叶测定生物量，采集样品500g带回实验室烘干求含水率。每块标准地设置9个2m×2m的小样方，采用收割法计算灌草本的生物量，进而计算出样地的生物量密度，最后统计整个森林生态系统的生物量。

2 结果分析

2.1 乔木单木生物量模型

在调查中，以胸径和树高（Vertex IV超声波测高仪）的测量精度最高，所以选取这两个指标作为建立模型的自变量，利用线性函数、指数函数、幂函数、二次函数模型，分别以D和D2H为自变量进行模型选优。

表1 以D为参数的单木生物量模型

分析表1可知，所拟合的线性、指数、幂、二次函数模型的F 值分别为 243.2、356.2、876.7、164.6，都表现为极显著性，在统计学上是成立的。幂函数B=0.201×D2.2的相关性最强，且误差值RS、AVGS、RMA最小，是以D为参数的最优模型。

以D2H为参数所拟合的线性、指数、幂、二次函数模型的显著性水平都是0，在统计学上表现为极显著，证明模型是合理的（表2）。在以胸径和树高的组合指标D2H为参数的拟合过程中，幂函数B=3.7×（D2H）0.95的相关系数又达到最大，且其误差值RS、AVGS、RMA也最小。

表2 以D2H为参数的单木生物量模型

分别比较以D和以D2H为参数的模型，选择相关系数最大的B=3.7×（D2H）0.95作为寒温带兴安落叶松单木生物量的模型，该模型的R值为0.923，F值、显著性分别为926.4和0.000，回归系数标准误差SEE值最小为0.207，说明模型的拟合效果较好。表明加入精确的树高指标，可以显著的提高生物量预测模型的精度。

2.2 样地草类生物量模型

备选模型1：假设直线通过原点，y的方差与x无关。

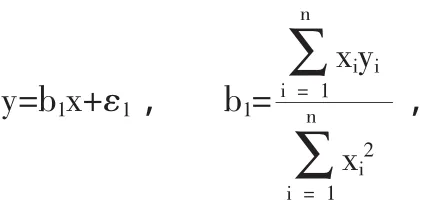
b1方差估计

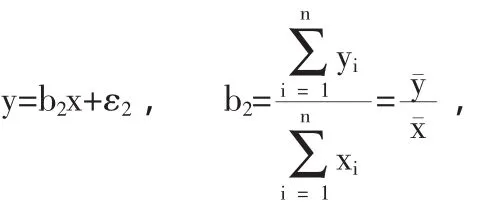
b2的方差估计：

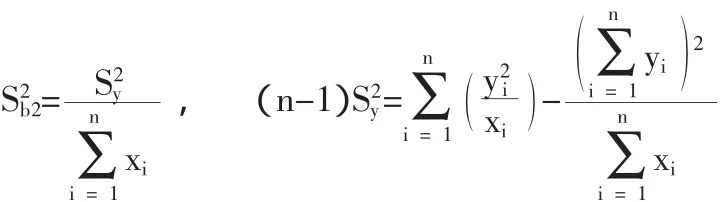
备选模型3：假设直线通过原点，y的标准差正比于x（δy=δx）。

b3的方差估计是

在模型1中，随机误差ε1满足ε1～N（0，δ2），即独立、正态、等方差。若观测数据满足假设条件时，模型对值的估计是最小无偏估计；若观测数据不能满足等方差的条件，则普通最小二乘法估计不再是最优估计。因此，必须变换模型1使其等方差，模型2和模型3正是出于这种考虑。通过计算比较备选模型b值的标准差，以最小标准差为准则，确定估计分量干质量的最适合模型（表3）。

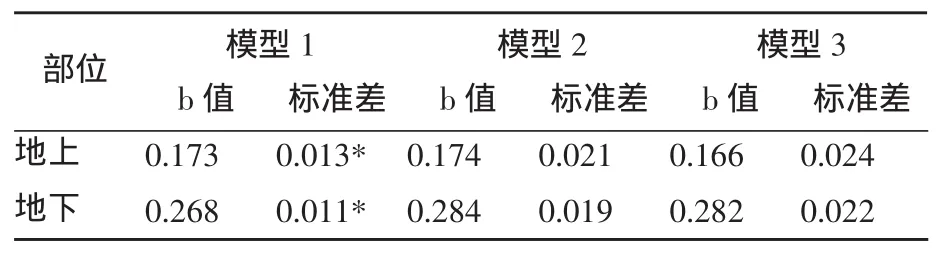
表3 草类3种模型干物质率b值的计算结果

2.3 样地灌木层生物量模型

灌木层分3个分量建模，分别为木质化部分、嫩枝叶和根。同理从2.2中的3种备选模型中进行优选。

经表4分析，除个别灌木的个别分量以模型3或模型2为优外，其它均以模型1最优。这说明变量满足模型1的前提条件：y的方差与x无关，即因变量y的估计误差与自变量x大小无关，各分量的干质量的估计误差与样品干质量、鲜质量的测量精度以及抽样误差有关。

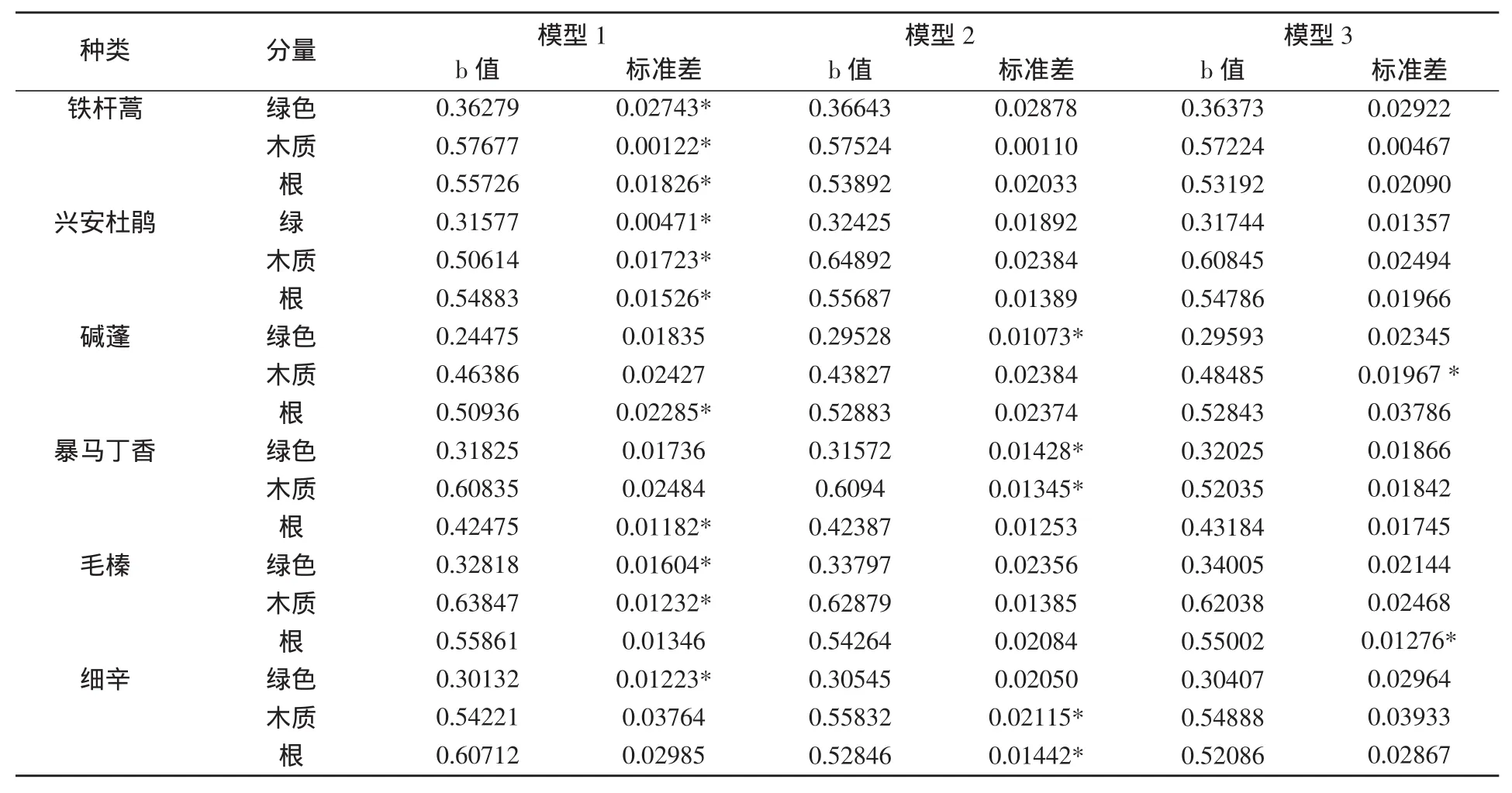
表4 灌木3种模型干物质率b值的计算结果比较

3 森林生态系统生物量模型的拟合

基于唐守正提出的生物量建模方法[13]，本研究以林分郁闭度C、平均林龄A、平均胸径D、平均树高H、林分蓄积V、林分密度N、胸高断面积B共计7个林分因子为自变量；以树冠生物量Wa﹑树干生物量Wb﹑树根生物量Wc、林木总生物量Wlm﹑灌木生物量Wgm、草本生物量Wcb、森林生物量W为因变量进行模型研究。同时，还将林木生物量的各分量，即木材﹑树皮﹑树枝和树叶生物量也作为因变量加以研究，分别以Wm﹑Wp﹑Wz和Wy表示。并对自变量之间、自变量和因变量之间的相关系数进行统计分析（表 5、表 6）。

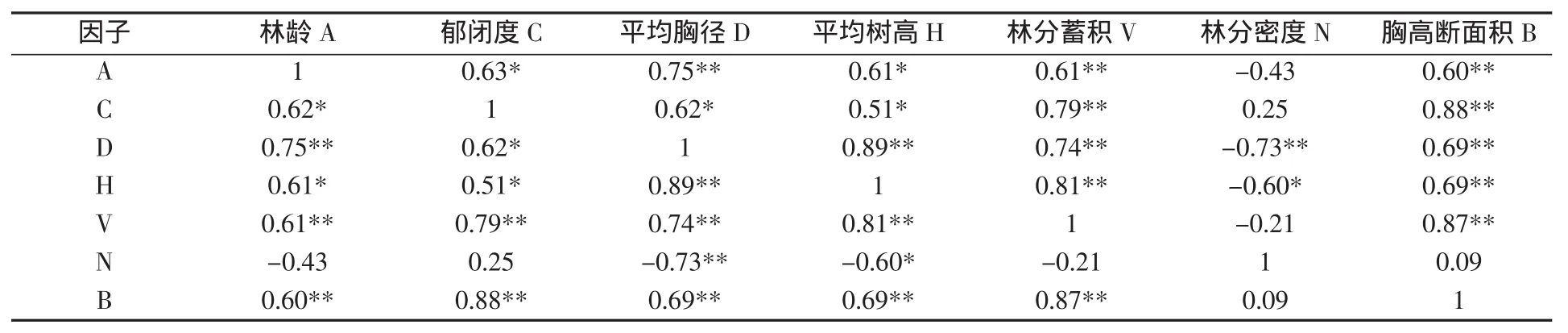
表5 兴安落叶松林分因子的相关系数

表6因变量与自变量（林分因子）的相关系数

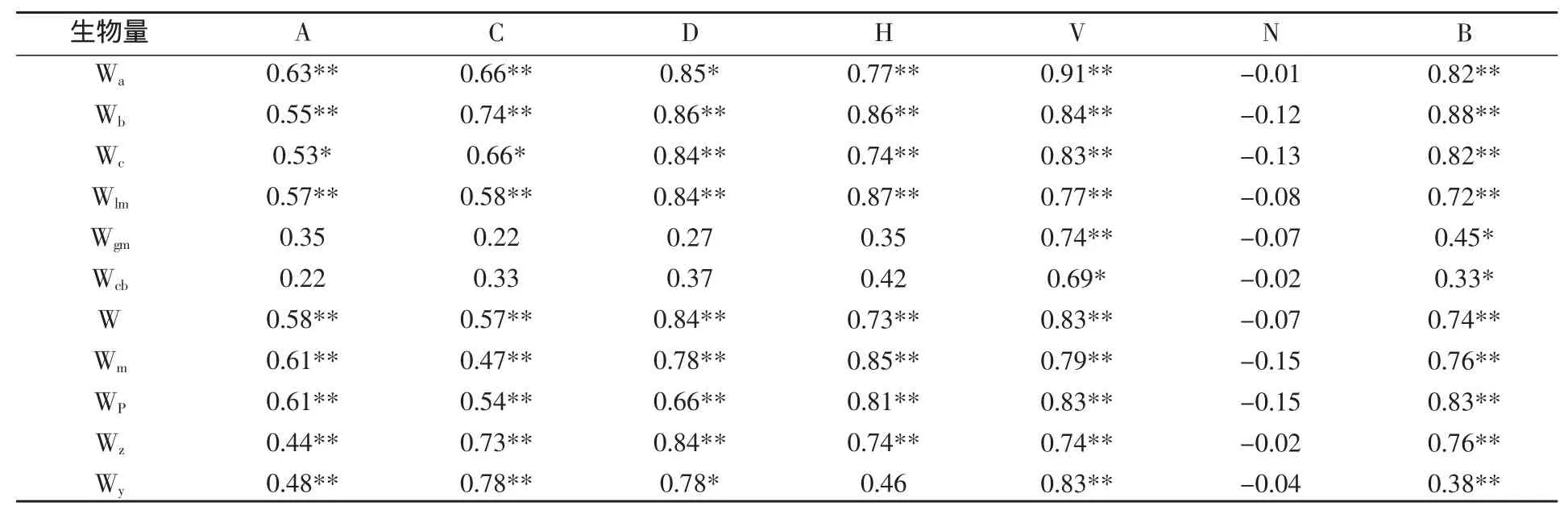
注：*表示显著性概率P值小于或等于0.05；**表示显著性概率P值小于或等于0.01

分析表5可知：林分蓄积和胸高断面积之间、平均树高和平均胸径之间均在统计上显著相关。这说明在建模的过程中，某些自变量可能并不重要，也可能质量较差，如果回归模型选入这些不必要的自变量，不仅计算量增大，还可能减弱回归方程的稳定性，直接影响模型的应用。所以要采用合适的变量优选法。

本研究采用逐步回归法对生物量模型进行联合回归以剔除不必要的因子，解决信息冗余问题。在7个自变量中，根据其对回归方程影响的大小，逐次的选入到回归方程中。在这个过程中，先前被选入的变量，有些由于其后新引入的变量而失去了重要性，这时就从回归方程中将它们剔除掉。每一步都进行了F检验，以保证每次引入新变量之前回归方程中只包含显著的变量。这个筛选过程用迭代法重复进行，直到回归方程中不再有可淘汰的变量，也没有再可引入的新变量为止，这时为理论上的最优模型（表7）。

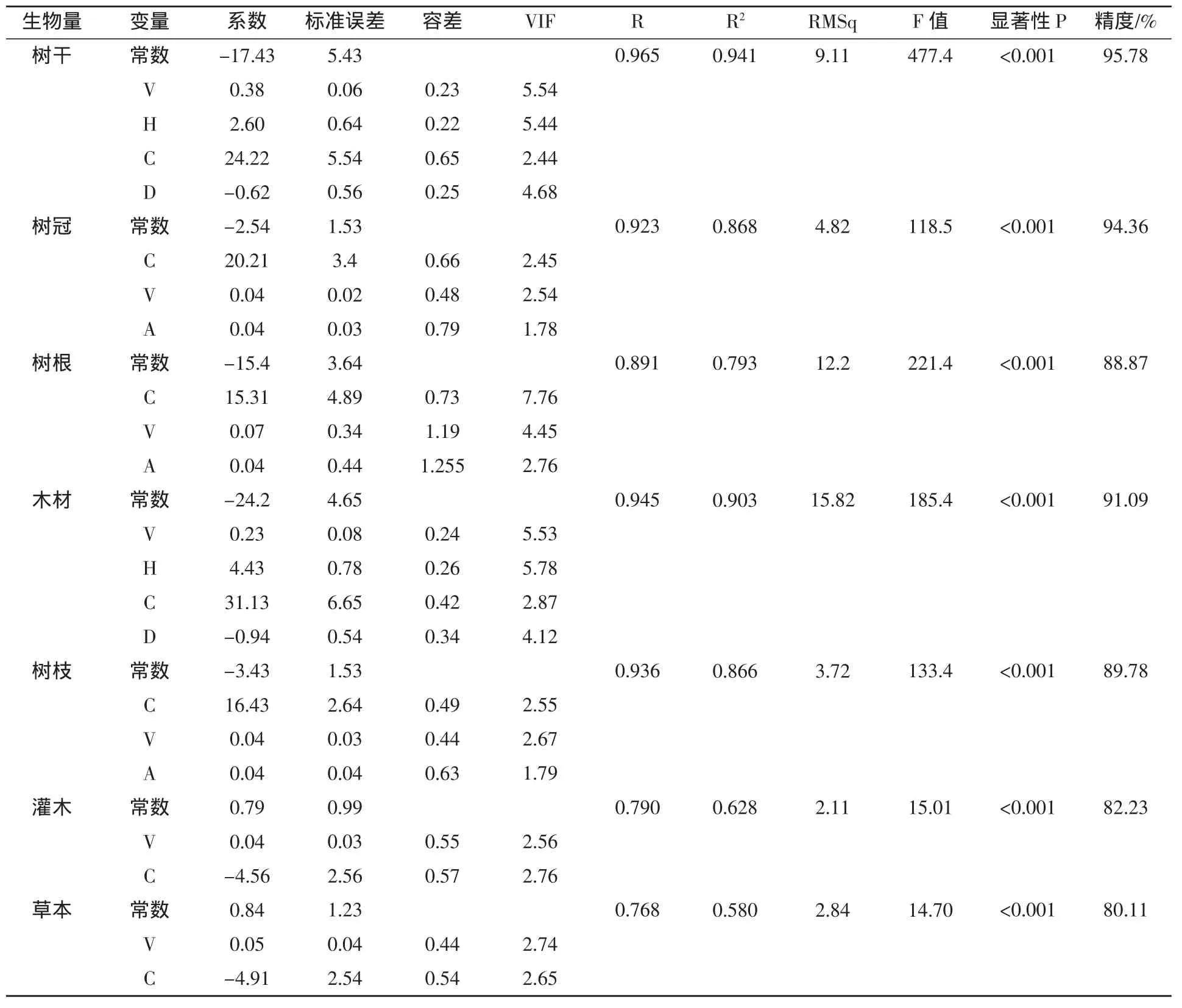
表7 逐步回归法拟合

在建模过程中，要对相关性大的变量进行取舍，平均林龄A和林分密度N在树干模型中被剔除，因为这两个变量和生物量的相关系数相对较小，虽然理论上样地的平均林龄越大，生物量的值将会越高，但实际中由于各种森林灾害造成的林木死亡和人为经营对密度的干预，使的平均林龄和样地的生物量关系相对较弱。同理，其它各分量的生物量模型也相应的去掉不必要的自变量，只选入有效参数进行建模。同时进行联合估计得到林木、树皮、树叶和森林总生物量模型（表8）。

表8 联合估计结果

4 结论与讨论

丰富的森林资源清查资料是了解各类森林材积准确信息的重要途径，如果能将这些资源用于估算森林生物量和生产力的动态变化，不仅对于科学地指导森林的经营管理，而且对于全球变化的研究，特别是区域尺度的生产力模型验证，都具有重要意义。本研究以兴安落叶松为例，探讨了利用森林资源清查资料估算森林生物量的方法，并建立了落叶松生物量和生产力的相关模型，为进一步基于森林资源调查资料估算其他类型森林生物量和生产力提高了技术参考。主要结论如下：

（1）以D2H为参数对兴安落叶松单木生物量拟合的精度高于仅以D为参数的模型，这和于立忠的研究结论一致[11]，但本研究的估测精度更高，原因是实验中利用了Vertex IV超声波测高仪进行了树高的测定，该仪器可以取得较高的测量精度，将准确的树高信息引入到模型中，必然提高模型的精度。幂函数B=3.7×（D2H）0.95在预测寒温带高山区兴安落叶松的单木生物量时表现最佳，该模型的R值达到0.92，F值和显著性分别为857和0.000，且其残差分布也符合要求，具有良好的统计学意义，这和刘兴良在四川地区选定的生物量幂函数模型相似[10]。研究表明林下灌木和草本生物量各分量的估计误差与样品干质量、鲜质量的测量精度以及抽样误差密切相关，而与样品本身的大小关系不大。

（2）在建立林分生物量模型的过程中，林分郁闭度、平均林龄、平均胸径、平均树高、林分蓄积、林分密度、胸高断面积这7个因子之间存在着较大的相关性，为了剔除掉冗余的信息，本研究利用的是逐步回归法对自变量进行优选，而李崇贵2005年对此问题采用岭迹分析法也同样取得了较高的精度。能否在该地区采用岭迹分析和主成分分析等方法解决信息重叠的问题以改善生物量模型，还有待于进一步研究。在建立的7个分量预估模型中，树干生物量的估测精度达到最高的95.78%；其次为树冠生物量，其精度为94.36%；林下灌木和草本层的估测精度较低。这主要是因为树干和树冠相对于林下植被，受到的人为干扰更小。通过联合估计得到的林木、树皮、树叶和森林总生物量模型也分别达到94.3%、91.22%、90.34%和93.43%的精度。但本研究的林分郁闭度数值大都为目测估计，在模型中并没能完全反映出对生物量的影响。建议在今后森林调查时，寻找更准确快捷的方法来测量郁闭度，以提高模型的可靠性。

在利用森林资源调查资料估算森林的生物量和生产力时不但要选好相关因子，而且也应该将人工林与天然林分别加以考虑。

［1］G.P Sparling，B.L Williams.Microbialbiomass in organic soils：Estimation of biomass C and effect of glucose or cellulose amendments on the amounts of N and P released by fumigation ［J］.Soil Biology and Biochemistry，1986，18（5）：507－603.

［2］Chen YH，Klinka K.Survival、growth、and allometry of planted Larix occidentalisseedlings in relation to light availability［J］.Forest Ecology and Management，1998，106（2-3）：169－179.

［3］Agnetha Alriksson，HilleviM.Eriksson.Variationsin mineral nutrient and C distribution in the soil and vegetation compartments of five temperate tree species in NE Sweden ［J］.Forest Ecology and Management，1998，108（3）：261－273.

［4］H.Jiang，Yu.Wang.Water Balance of Birch and Larch Leaves and their Resistance to Short and Progressive Soil Drought［J］.Russian Journal of Plant Physiology，2004，60（5）：697－701.

［5］G.S Zhou，M.Zhao.Estimation ofbiomassand net primary productivity of major planted forests in China based on forest inventory data［J］.Forest Ecology and Management，2005，207（3）：295－313.

［6］程云屑，李忠孝.兴安落叶松三个主要林型森林生物量的初步研究［J］.内蒙古林业调计，1989，（4）：29－39.

［7］陈林娜，盖强.庞泉沟自然保护区华北落叶松森林群落生物量的初步研究［J］.山西农业大学学报（自然科学版），1991，11（3）：240－247.

［8］王喜武，李喜运.长白落叶松生物量测定的初步探讨［J］.辽宁林业科技，1993，（6）：31－34.

［9］王永祥，吴耀先.兴安落叶松人工林生物量及器官分配规律的研究［J］.辽宁林业科技，1999，（2）：17－20.

［10］刘兴良，汪明，宿以明，等.川西高山林区人工林生态学研究-种群结构［J］.四川林业科技，2003，（3）：1－9.

［11］于立忠，丁国泉，朱教君，等.施肥对兴安落叶松人工林细根生物量的影响［J］.应用生态学报，2007，18（4）：713－720.

［12］艾训儒，沈作奎.中亚热带兴安落叶松生物量、生长量研究［J］.湖北民族学院学报（自然科学版），2001，19（2）：20－22.

［13］唐守正，张会儒，胥辉.相容性生物量模型的建立及其估计方法的研究［J］.林业科学，2000，36（增刊 1）：19－28.