某机载雷达发射座架振动数值分析*
2015-09-08杜振勇时社萍梁震涛
杜振勇,时社萍,梁震涛
(南京电子技术研究所, 江苏 南京 210039)
某机载雷达发射座架振动数值分析*
杜振勇,时社萍,梁震涛
(南京电子技术研究所, 江苏 南京 210039)
采用数值分析方法对某机载雷达中发射座架进行随机振动响应研究,得到了发射座架的模态和应力分布云图。其上定位销的最大应力已经处于危险状态,根据应力分布结果,提出了台阶式定位销改进方案,并对新方案的发射座架进行了数值分析。研究结果表明,采用新式定位销的发射座架可以满足某雷达的隔振要求。
雷达;随机振动;数值分析
引 言
飞机在起飞、着陆和空中飞行时,与空气、地面发生摩擦会产生随机振动、冲击载荷。此外,飞机在空气中受空气动力、弹性力和惯性力的耦合作用时会发生自激振动[1]。在如此复杂的环境下,机载雷达的工作安全性和可靠性是设计师重点关注的问题[2-4]。发射单元是雷达系统的重要组成部分,其结构动力学性能直接影响波形和信号增益等电讯参数,进而影响雷达整机的可靠性。发射座架作为发射单元的基础结构,直接影响发射单元的性能,因此在结构设计阶段,必须对发射座架进行刚强度分析与校核。本文针对机载发射座架的振动环境,利用Pro/E对发射座架进行了建模,利用Hypermesh对其进行了网格划分和约束。为节约运算时间,提高效率,将发射单元、接收馈线组件等结构简化为含惯性信息的质点。利用ANSYS软件对发射座架有限元模型进行了模态分析和随机振动分析,得到了其在载荷谱激励下的应力和变形云图。
1 产品结构及有限元模型
1.1产品结构
发射机主要由发射座架、发射单元、馈线单元和波导等结构组成。发射单元固定在发射座架上,然后通过发射座架与飞机相连。发射单元通过2个定位销、9个螺钉与发射座架固定,后面使用定位销限位,总体连接采用前锁紧后定位的形式。发射座架的结构形式如图1 所示。
1.2有限元模型
根据实际结构合理简化模型是正确进行有限元分析的基础。发射单元结构相对复杂,对整个结构的刚强度影响不大,元件可以简化为质点单元,保留该元件的等效质量和惯性变量。同时,为了提高分析效率,将模型中的倒角、圆角等对分析结果影响较小的几何特性去除,予以简化。根据产品安装形式,发射座架上的各单元可以简化为质量点,采用实际模型的重量及惯性矩进行模拟,大大降低了计算量。

图1 发射座架整体结构
基于Pro/E构造三维简化模型,并将其导入Hypermesh进行网格划分。对每个零件实体进行材料属性的定义,实体模型选用实体单元solid187,质量单元选用mass21。接触选用六自由度绑定约束和四自由度圆柱副约束分别模拟螺钉和定位销。其中,9个螺钉与发射座架固定采用六自由度约束,限制了各零件间在接触面的相对滑动,2个定位销与发射座架的限位采用四自由度圆柱副模拟,保留了定位销绕中轴线的转动及平移自由度。
有限元网格划分时,对结构进行了切割处理,规则部分采用映射划分,不规则部分采用精细化自由划分。发射机的有限元模型如图2所示,共有133 709个单元,253 204个节点。

图2 发射单元有限元模型
2 模态分析
在随机振动分析前,需求出发射座架结构的固有频率和模态振型,这是对结构进行解耦的必要条件。随机振动试验是将试验件安装于单自由度振动的试验平台上,随着平台进行单自由度随机振动,分别进行3个方向的随机振动即可。
各方向的随机振动方程相同,以X方向的随机振动为例,发射座架在X方向的动力学方程为:
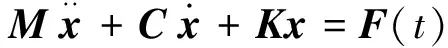
(1)

对于模态分析,求解系统的固有频率和模态振型,F(t)=0,C一般可以忽略。因此,无阻尼自由振动系统的动力学方程为:

(2)
设x=Asin(ωt),A为振幅,带入式(2)得:
(3)
式中,ωi为系统的第i阶圆频率,fi=ωi/2π为第i阶固有频率。
发射座架由铝合金5A05(H112)制成,其抗拉强度σb=275 MPa,弹性模量E=7.0 × 1010Pa,泊松比μ=0.2,密度ρ=2 700 kg/m3;定位销采用优质热压圆钢45,其抗拉强度σb=600MPa,弹性模量E=2.1×1011Pa,泊松比μ=0.3,密度ρ=7 600 kg/m3。
对发射座架进行模态分析得到前5阶固有频率和对应振型分别如表1和图3~图7所示,均为发射座架边缘振动幅度最大。

表1 固有频率结果
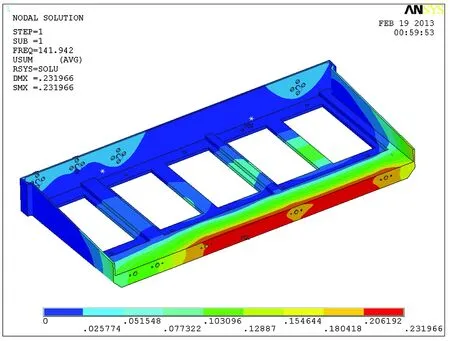
图3 第1阶模态
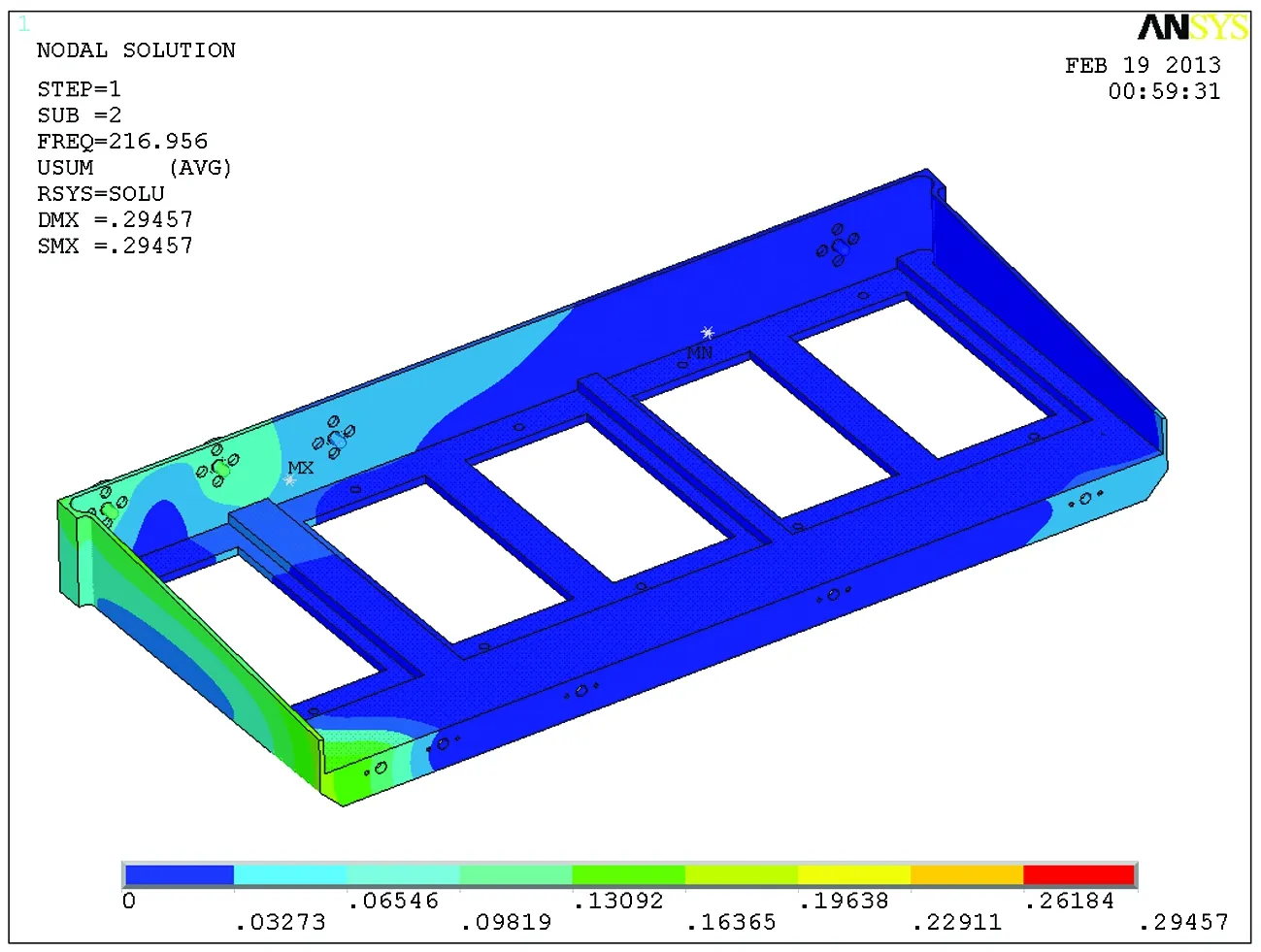
图4 第2阶模态

图5 第3阶模态

图6 第4阶模态
3 随机振动分析
3.1环境试验条件
该雷达发射机在工作状态时,承受载机的宽带随机振动激励范围是15~2 000 Hz[4],随机振动谱线如图8所示。

图8 随机振动谱线
3.2随机振动分析
传统虚拟激励法[5]的求解较为繁琐,采用改进的绝对位移直接求解的虚拟激励法[6]求解,则发射座架随机振动动力学方程可以写成:
(4)
其中,下标zy和gd分别表示结构的自由和固定节点,因此Fzy=0,假设固定点虚拟加速度激励为a=λeiωt,则固定点激励即振动的试验平台的激励为:
Fgd=Mgdλeiωt
(5)
将式(4)第2行展开并化简得:
Mgd-1(Kgdzyxzy+Kgdxgd)=λeiωt
(6)
当Mgd质量很大时,固定点虚拟加速度激励可等效为:
(7)
由此可得:
(8)
将式(7)和式(8)代入式(4)第1行展开并化简得:
(9)
(10)
3.3刚强度校核
随机振动分析结果如表2所示,从分析结果可知,发射座架结构的最大变形值为0.532 mm,1σ最大von-Mise应力的解为σ=162 MPa,为X方向振动激励下的应力响应,如图9、图10所示,3σ最大von-Mise应力的解为σ=486 MPa,应力最大处位于定位销根部,材质的抗拉强度为600 MPa,安全系数f仅为1.2,无法达到1.5,振动时定位销存在破坏风险,因此需要对结构进行改进。

表2 随机振动分析结果

图9 X方向振动激励下的应力响应
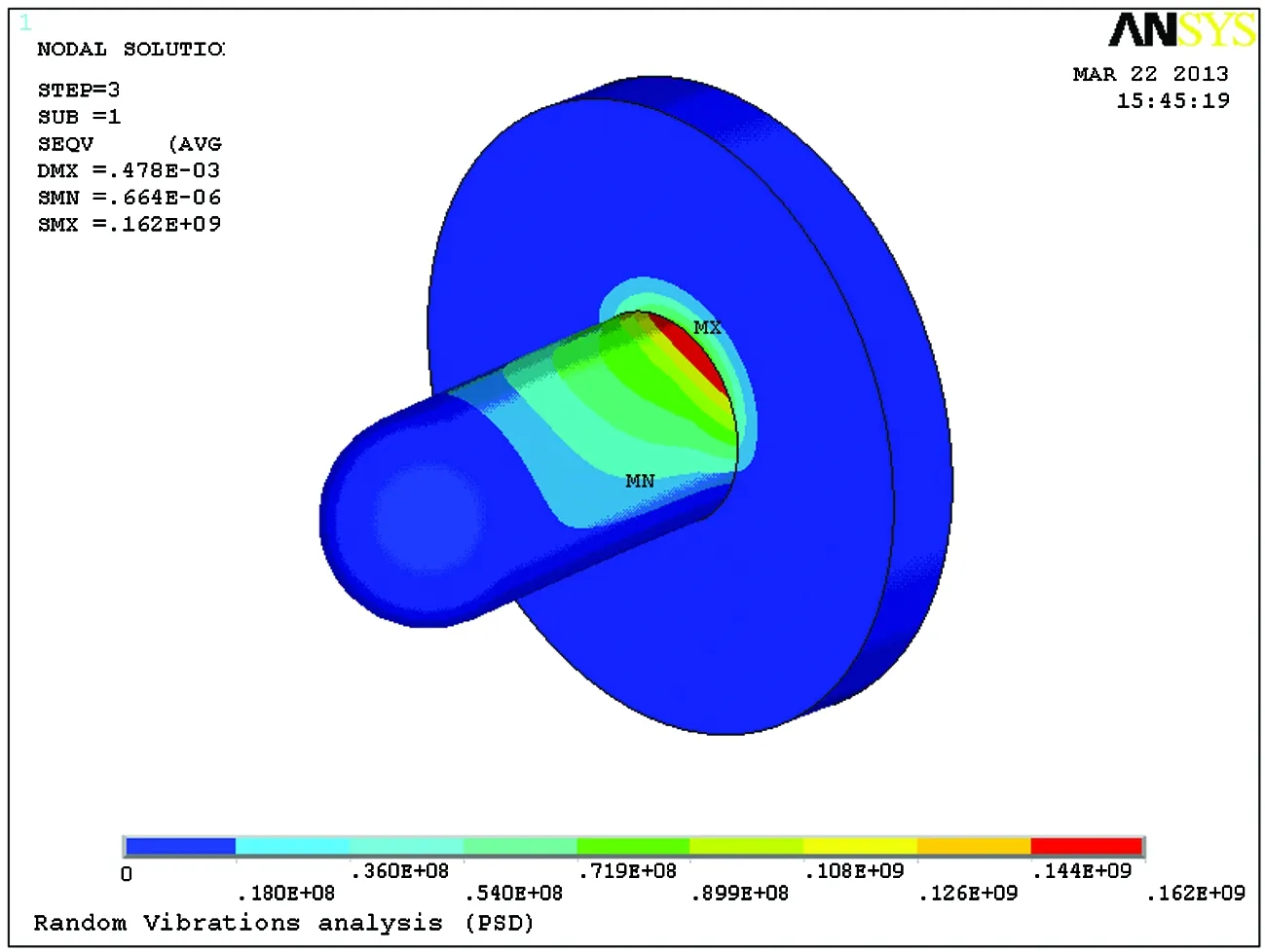
图10 X方向振动激励下定位销的应力响应
改进后的方案增加了凸台结构,使得根部抗弯刚度增大。改进后进行振动分析,3σ最大von-Mise应力的解为σ=324 MPa,如图11、图12所示,安全系数f为1.8,超过1.5,由此可知在设计寿命内结构安全。发射座架结构设计满足机载环境下的振动刚度和强度要求。

图11 改进后X方向振动激励下的应力响应
该发射座架实物通过了环境试验的考验,并已正式交付用户使用,使用情况良好,这也验证了软件分析结果的可靠性。
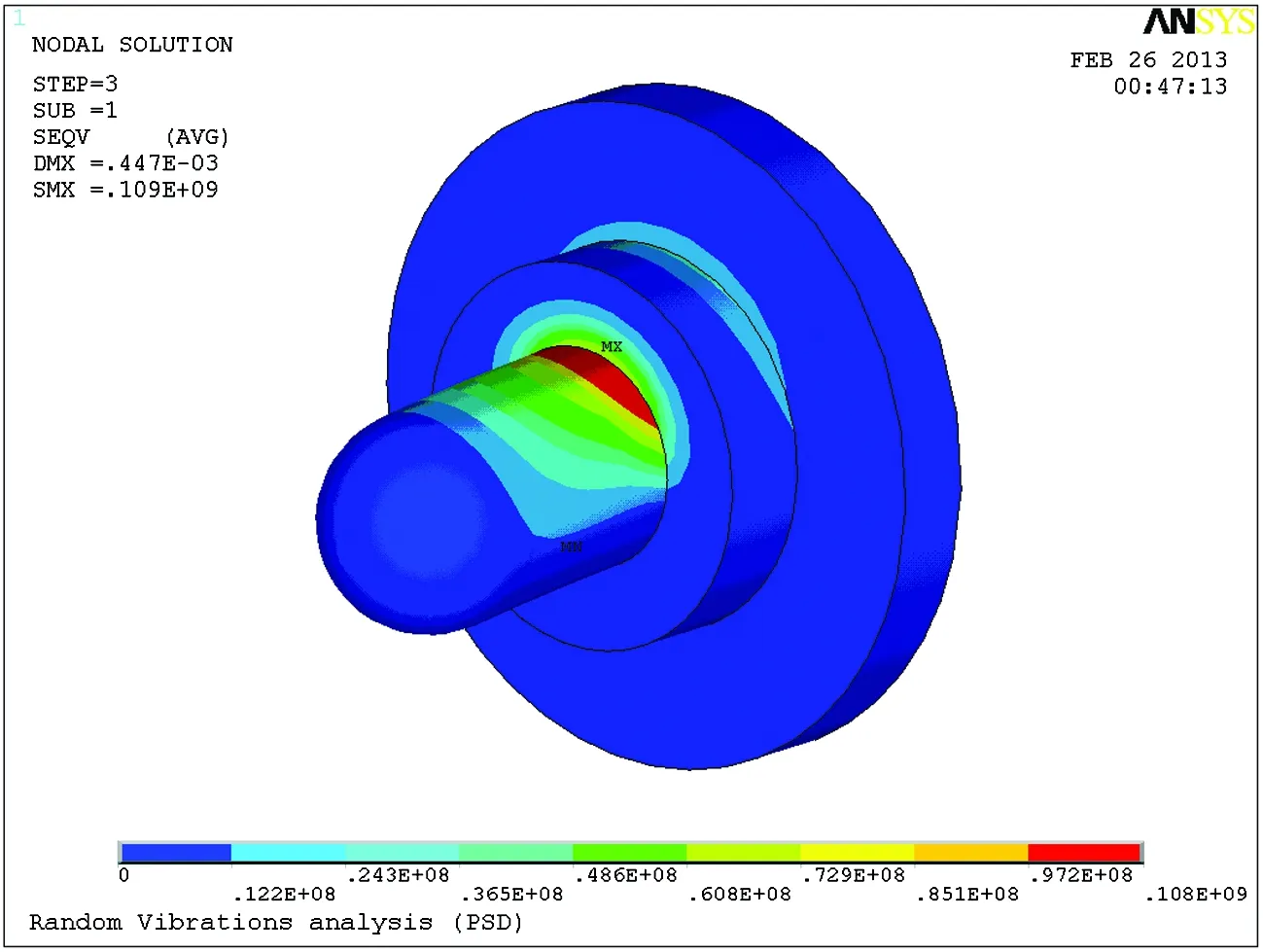
图12 改进后X方向振动激励下定位销的应力响应
4 结束语
本文针对机载雷达发射座架的结构特点,利用ANSYS建立了发射座架的有限元动力学模型,并对发射座架进行了模态分析。考虑载机的振动环境条件,进一步对发射座架进行了随机振动响应分析,得到了三自由度振动台的位移解析方法及功率谱密度表达式。完成了发射座架定位销的振动强度校核,根据分析结果将定位销改进为台阶式定位销,经过数值分析,台阶式定位销设计更为合理,满足结构要求。该研究为发射单元的结构优化和减重设计提供了重要依据。
[1] 刑誉峰, 李敏. 工程振动基础[M]. 北京: 北京航空航天大学出版社, 2011.
[2] 洪长满, 段勇军. 机载雷达天线座结构的刚强度性能评估[J]. 现代雷达, 2011, 33(6): 72-75.
[3] 段勇军, 顾吉丰, 平丽浩. 雷达天线座模态分析与试验研究[J]. 机械设计与制造, 2010(2): 214-216.
[4] 矫志宁. 某机载雷达发射机的随机振动分析[J]. 电子机械工程, 2013, 29(2): 18-20, 23.
[5] 林家浩, 张亚辉. 随机振动的虚拟激励法[M]. 北京: 科学出版社, 2004.
[6] 李永华, 李思明. 绝对位移直接求解的虚拟激励法[J]. 振动与冲击, 2009, 28(10): 185-190.
杜振勇(1982-),男,工程师,主要从事结构设计及分析工作。
VibrationNumericalAnalysisoftheTransmitterPedestalofanAirborneRadar
DUZhen-yong,SHIShe-ping,LIANGZhen-tao
(NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)
The random vibration response of the transmitter pedestal used in an airborne radar is studied based on numerical analysis method. The modal and stress distribution of the transmitter pedestal are obtained. The result shows that the positioning pins on the transmitter pedestal are in risky state. A new improvement design of step-type positioning pin is proposed according to the stress distribution. Numerical analysis shows that the new positioning pins can satisfy the vibration isolation requirement of the radar.
radar; random vibration; numerical analysis
2015-06-05
TB535
:A
:1008-5300(2015)04-0001-04
