某星载电子设备的力学仿真分析*
2015-09-08吴孟武黄春江
吴孟武,黄春江
(南京电子技术研究所, 江苏 南京 210039)
某星载电子设备的力学仿真分析*
吴孟武,黄春江
(南京电子技术研究所, 江苏 南京 210039)
星载电子设备面临着各种严酷的力学环境,具有极高的可靠性要求。文中为了节省环试成本,缩短研发周期,采用ANSYS建立了某星载电子设备的力学仿真模型;为了验证模型的准确性,进行了该电子设备的模态仿真及实测,经过比较发现两者数据非常接近;基于建立的仿真模型,分析了该电子设备在加速度过载、冲击、正弦振动及随机振动等各种工况下的结构响应和受力情况,得到了相应的位移和应力云图。结果表明该电子设备的结构设计满足星载环境要求。文中针对该电子设备的结构仿真及测试对于理解其力学特性具有重要的意义。
星载电子设备;力学仿真;模态测试;随机振动
引 言
星载电子设备在运输、发射、飞行等过程中要经受各种严酷的力学环境考验,如加速度、噪声、冲击、振动等。力学环境可导致电子设备结构变形或损坏,具体表现为:电子元器件受损;仪器设备因电子线路断路、接插件松动和支架断裂而发生故障;结构遭到破坏或断裂等。这些故障可能影响到任务的完成,甚至导致任务失败[1-5]。鉴于星载电子设备具有极高的可靠性要求,因而在其产品研制过程中,就要求综合其寿命周期内的各种力学环境,在地面进行相应的鉴定级环境试验。近年来,随着星载型号研制任务的不断推出,降低研制成本、缩短研发周期的要求也越来越迫切,传统的“设计—试验验证—设计—试验验证”研制思路已不能满足上述要求。

本文以星载雷达中某重要电子设备为研究对象,采用通用大型有限元分析软件ANSYS建立了对应的力学仿真模型;应用该仿真模型,对该电子设备的模态特性进行了仿真分析;基于LMS振动测试系统对其进行了模态实测;通过仿真结果与实测数据的对比,较好地验证了力学仿真模型的准确性;基于建立的仿真模型,结合该电子设备的设计要求,对其在加速度过载、冲击、正弦振动及随机振动等各种工况下的结构响应和受力情况进行了分析,得到了对应的安全裕度数据,并以此判断该电子设备的结构设计是否满足星载环境要求。
1 有限元模型的建立
1.1模型简化及网格划分
由于比较关注结构的整体动力学特性,因此此次力学仿真分析以该电子设备结构星阶段的模型为研究对象,如图1所示。该电子设备结构星模型整体上由机壳、盖板、侧板3部分组成。机壳与盖板、机壳与侧板均采用沉头螺钉连接。在机壳的底面,设计有6个安装支耳,这些支耳采用螺钉连接的方式将整个设备直接固定在卫星安装平台上。
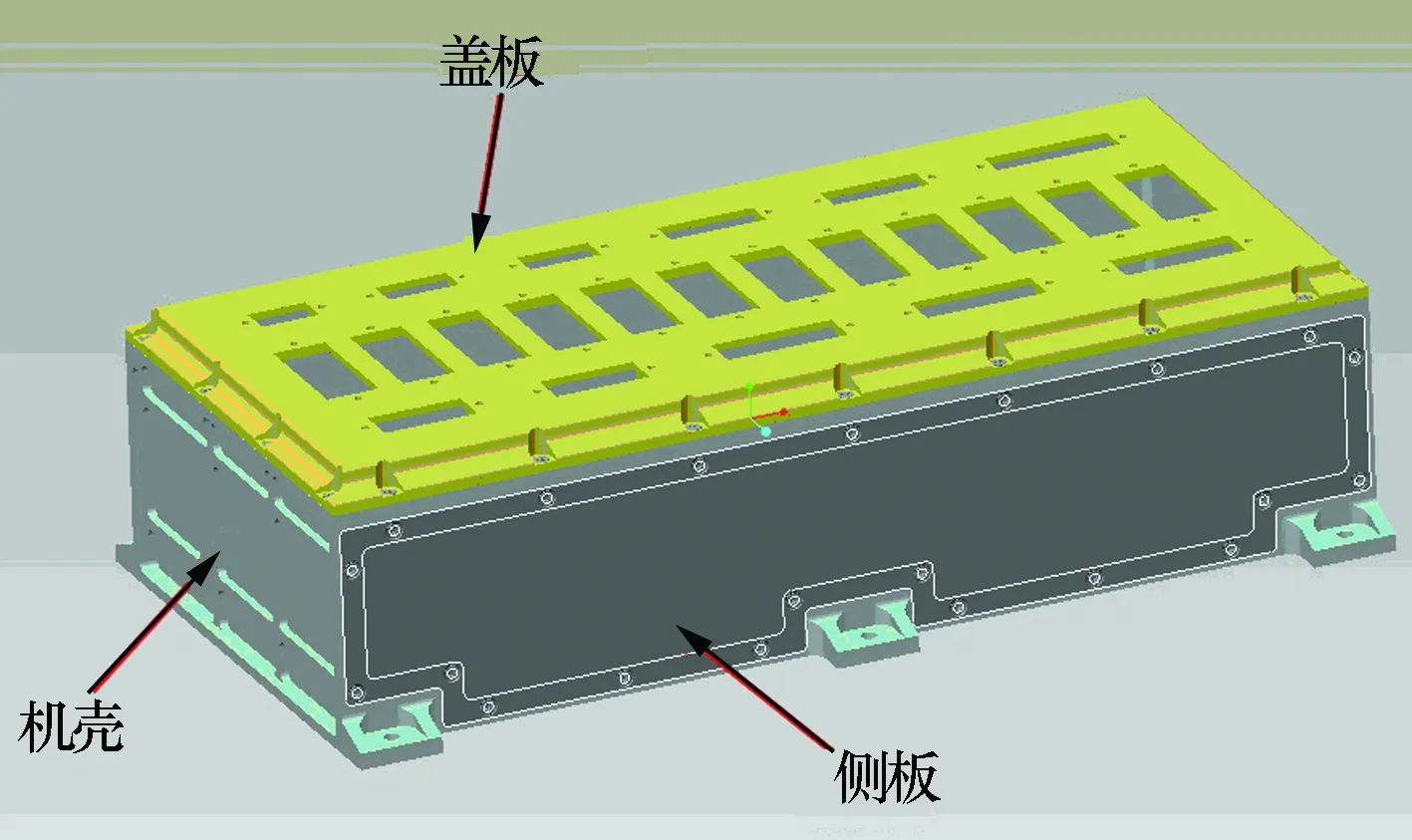
图1 电子设备结构模型
文中综合考虑仿真计算效率及模型准确度等因素,对电子设备结构星模型进行了一定程度上的简化处理:去掉尺寸较小的孔、凸台、圆角;去掉不必要的倒角;将螺钉连接简化为有限元模型中结点之间的自由度耦合等。在模型简化的基础上,以四面体网格为基础,采用网格局部加密技术得到网格模型,如图2所示,其中网格总数量为111 303个,节点数为213 950个。该电子设备机壳、盖板及侧板材料均选用铝合金5A05,其力学性能见表1。

图2 模型简化及网格划分

表1 铝合金5A05力学性能
1.2边界条件的设置
依据星载环境条件的要求,该电子设备需承受加速度过载、冲击、正弦振动及随机振动等恶劣工况而不发生破坏和失效。表2~表5列出了各种工况下对应的试验条件,本次力学仿真将其作为载荷输入从而计算得到对应的结构响应和受力情况。

表2 加速度试验条件

表3 冲击试验条件
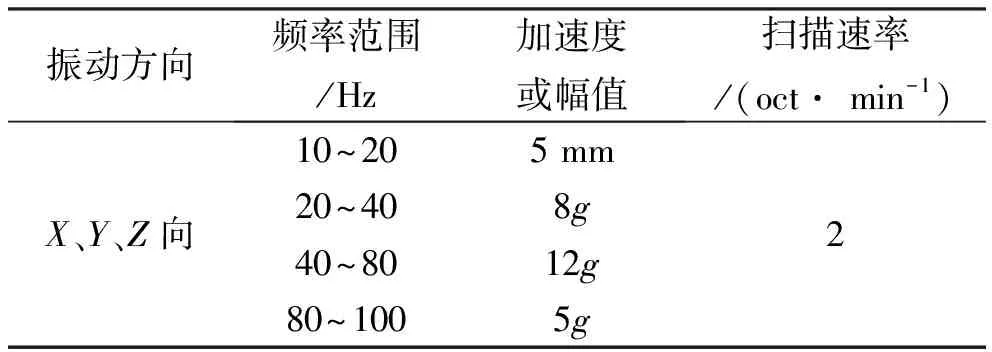
表4 正弦振动试验条件

表5 随机振动试验条件
2 模态仿真及实测
按照仿真计算规范流程,仿真模型建立后,需进行验模工作,以保证后续仿真计算结果的准确性和可信度。在验模过程中,当发现仿真结果与实际结果有较大差异时,需对仿真模型进行修正(修正材料参数、结构参数,调整网格划分数量及质量等),如此反复直至仿真结果与实际结果差距在允许的范围内。
为了验证建立的力学仿真计算模型的准确性,本文对该电子设备进行了模态仿真及实测。模态分析是动态响应分析的基础,其最终目标是识别出系统的模态参数,为结构系统的振动特性分析、振动故障诊断及结构动力特性的优化设计提供依据。
2.1模态仿真
模态分析待求的参数是结构的固有频率和振型,在本次仿真计算中,采用Lanczos方法计算该电子设备自由态及约束态下各阶固有频率,并得到对应的模态振型。
根据相关振动理论,结构的低阶模态对振动响应的影响较大,高阶模态可以忽略不计。表6列出了通过仿真计算得到的该电子设备自由态及约束状态下(6个支耳固定支撑)前6阶的固有频率及模态振型最大变形位置。对于自由态而言,由于不施加任何约束,结构在3个方向平动及转动发生的是刚体位移,此时前6阶模态频率基本为0。因此对于自由态,处理方式为将第7阶模态当做第1阶模态。图3为约束状态下该电子设备前6阶的模态振型。

表6 自由态和约束态下前6阶模态频率及振型最大变形位置

图3 约束状态下前6阶模态振型
从表6及图3可以看出:自由态下前6阶模态振型的最大变形均发生在盖板上,而约束态下除第3、第6阶模态振型最大变形发生在机壳底面上外,其余4阶也均发生在盖板上。此时2种状态下的模态频率相近,且模态振型位置和幅度也相近。其原因在于:对于该电子设备主体结构而言,盖板是相对薄弱的部位,所以前几阶模态振型通常发生在盖板上;由于与机壳相比,盖板配重较轻,而约束状态下是对机壳底面6个安装支耳进行固定支撑,此时对于盖板而言,自由态与约束态时的工况变化并不大,所以2种状态下盖板的模态频率及振型相近。从表6还可以看出,该电子设备最低的固有频率大于500 Hz,远大于正弦振动条件下扫频最高频率(100 Hz),也即结构设计有效地避开了外部工作激励频率,结构不会产生共振现象。
2.2模态测试
模态试验选用比利时的LMS Test Lab Rev 8B进行数据采集和模态分析,加速度传感器与力锤分别采用美国PCB公司的PCB 333B32及PCB 086C03。图4为该次模态测试的原理示意图。其中电子设备放置于极柔软的海绵上,几乎等同于自由工况。由前期仿真分析可知,自由态下前6阶模态振型的最大变形均发生在盖板上。为了有效捕捉激励响应,试验时加速度传感器均布置在盖板上,且采集方向与盖板垂直。另外,力锤锤击位置选取盖板右下角,方向也与盖板垂直。
表7列出了由试验实测得到的该电子设备自由态下前6阶的固有频率。从与表6中自由态下模态仿真结果进行的对比可知:仿真结果与试验结果非常接近,至第6阶时两者数值误差仍在7.1%以内。模态仿真与实测以及两者结果的对比,充分验证了本文建立的力学仿真模型的准确性。
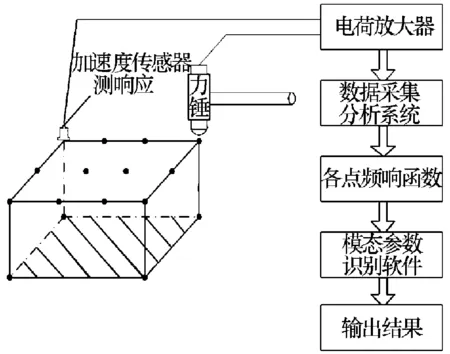
图4 模态测试原理示意图

表7 实测得到的自由态下前6阶模态频率
3 力学仿真及结果分析
3.1加速度过载仿真及结果分析
此次加速度过载仿真采用静力分析方法进行,输入条件见表2。图5及表8为仿真计算得到的该电子设备在3个方向加速度过载下的结构受力及变形情况。

图5 加速度过载下应力云图及变形云图

表8 加速度过载下最大应力及变形
表8中安全裕度的计算公式为

式中:MS为安全裕度;[σ]为最大许用应力,在此即为铝合金5A05的屈服强度值125 MPa;σmax为计算得到的最大应力;f为安全系数,金属材料的安全系数通常取为1.5。从图5及表8可以看出:在加速度过载载荷下,该电子设备的应力最大值出现在机壳安装支耳处,结构设计完全满足加速度过载环境要求。
3.2冲击仿真及结果分析
按照表3中的冲击环境条件,对该电子设备进行瞬态动力学仿真,在有限元分析中,冲击载荷施加在基础节点上。半正弦波的加速度峰值为50g,持续时间为11 ms,在5.5 ms时达到最大值。考虑到结构阻尼,仿真中将阻尼系数设为0.02。瞬态分析过程采用完全法,仿真计算时间持续至20 ms,以捕捉到整个冲击过程中的结构响应。
图6为仿真计算得到的整个冲击过程中结构的最大应力节点应力-时间历程曲线。从图6可以看出:由于结构阻尼的存在,整个冲击过程中3个方向的最大应力并没有出现在5.5 ms处,而是滞后了一段时间,大约出现在6 ms处;冲击载荷加载至11 ms时结束,而结构响应仍然持续了一段时间。最大应力滞后和结构响应的持续与结构的特性是相吻合的。

图6 冲击载荷下最大应力节点应力-时间历程曲线
图7为仿真计算得到的在3个方向冲击载荷作用下结构的最大应力及变形云图,表9则对结构的最大应力、最大变形及发生的位置进行了统计。从图7和表9可以看出:与加速度过载载荷相比,冲击载荷更为恶劣;该电子设备在Y向冲击载荷作用下,最大应力达到了20.29 MPa,且仍出现在机壳安装支耳处。尽管如此,结构设计仍然具有正的安全裕度(最小为3.1),也即该电子设备结构设计满足冲击环境要求。

图7 冲击载荷下最大应力云图及变形云图

表9 冲击载荷下最大应力及变形
3.3正弦振动仿真及结果分析
基于前期模态仿真结果,正弦振动仿真采用谐响应分析方法进行,输入条件见表4。由于正弦振动载荷分为加速度及位移2类,因此在进行仿真计算时,应依据不同的频率范围,分段进行谐响应分析。
从仿真计算可知:该电子设备在频率点80 Hz时,结构响应最为剧烈,此时结构发生的变形最大,承受的应力也最大。图8及表10为该电子设备在3个方向正弦振动载荷下于80 Hz频率点处的结构受力及变形情况。从图8及表10可以看出:与加速度过载及冲击载荷相比,正弦振动对该电子设备的影响最小,结构应力值及变形值均较低,结构设计具有较高的安全裕度。

图8 正弦振动载荷下应力云图及变形云图(80 Hz)

表10 正弦振动载荷下最大应力及变形
3.4随机振动仿真及结果分析
以模态仿真结果为基础,随机振动仿真采用PSD方法进行。将表5所示试验条件作为载荷输入,图9为对应的功率谱密度曲线。分别提取3个载荷方向的3σ应力及3σ变形,如图10及表11所示。

图9 随机振动功率谱密度曲线
从图10和表11可以看出,与加速度过载载荷、冲击载荷及正弦振动载荷相比,随机振动载荷的工况最为恶劣。在Y向随机振动载荷作用下,最大3σ应力达到了73.16 MPa,最大3σ变形则达到了0.39 mm。最大3σ应力出现在机壳底面安装支耳处,而最大3σ变形则出现在盖板中心处。最大3σ应力和最大3σ变形出现的位置与该电子设备的结构形式是相符的:该电子设备结构在垂直方向(Y向)的刚强度较薄弱,仿真计算时,在Y向载荷作用下,结构的受力及变形明显大于另外2个载荷方向;机壳安装支耳处作为与卫星平台的安装接口,在Y向载荷作用下,必然承受最大的拉应力;此时盖板作为刚度最薄弱的环节,在盖板中心发生最大的垂直变形。计算得到的结构安全裕度最小值为0.1(见表11),仍然大于0,也即该电子设备的结构设计满足随机振动环境要求。

图10 随机振动载荷下3σ应力云图及3σ变形云图

表11 随机振动载荷下最大3σ应力及3σ变形
4 结束语
本文针对星载电子设备地面环境试验周期长、成本高、开展困难等现状,在产品设计阶段即采用数值仿真技术,对某电子设备的结构设计进行了仿真验证,大大缩短了产品的研发周期,降低了研发成本。按照标准的仿真分析流程,建立力学仿真模型(涉及到模型简化、网格划分及设置边界条件等),进行模型验证(将模态仿真结果与实测结果进行对比),再基于准确的仿真模型,对星载电子设备在加速度过载、冲击、正弦振动及随机振动等各种工况下的结构响应和受力情况进行分析,得到了对应的安全裕度数据。结果表明,该电子设备结构设计满足星载环境要求。
文中针对该星载电子设备的结构仿真及测试对于理解其力学特性具有重要的意义,同时其仿真分析流程及思路也具有较大的借鉴意义。
[1] 管宇辉. 某星载设备环境综合仿真[J]. 机械研究与应用, 2013, 26(6):88-90.
[2] 王长武. 星载雷达天线结构动态特性研究[J]. 现代雷达, 2008, 30(5): 119-122.
[3] 周冠杰, 赵玉洁. 星载雷达结构设计的特点[J]. 电子机械工程, 2008, 24(2): 35-40.
[4] 王恒海, 邵奎武. 星载雷达发射机支撑架结构优化设计及动力学分析[J]. 电子机械工程, 2011, 27(1): 39-46.
[5] 程丹, 王长武. 一种星载雷达T/R组件与波控单元连接设计[J]. 电子机械工程, 2015, 31(1): 32-34.
[6] 刘树斌, 闻月娇, 王志成. 某星载电子设备的动态响应分析[J]. 机电产品开发与创新, 2014, 27(4): 106-107.
吴孟武(1984-),男,工程师,主要从事军用雷达电源及配电结构设计工作。
黄春江(1971-),男,高级工程师,主要从事军用雷达电源结构设计工作。
MechanicalSimulationAnalysisofaSpace-borneElectronicEquipment
WUMeng-wu,HUANGChun-jiang
(NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)
Extremely high reliability for the space-borne electronic equipment is required for it has to face various severe environments during the launching stage and in the space. In order to reduce the cost of environmental tests and shorten the development cycle, the mechanical simulation model of a certain space-borne electronic equipment is established by ANSYS software. Modal simulation and test are both carried out to verify the simulation model. The result shows that the simulation data and test data are almost the same. Based on the simulation model, the acceleration overload, impact resistance, sinusoidal vibration and random vibration performance of the electronic equipment are analyzed and the corresponding mechanical response data such as deformation and stress are obtained. The result shows that the mechanical design of the electronic equipment satisfies the strength requirement in the space-borne environment. The mechanical simulation and test in this paper are very helpful for understanding the mechanical characteristics of the space-borne electronic equipment.
space-borne electronic equipment; mechanical simulation; modal test; random vibration
2015-07-13
TP391.99
:A
:1008-5300(2015)04-0049-08
