基于Lattice-Boltzmann方法的纳米颗粒多孔介质导热特性

阚安康，康利云，曹丹，王冲

（上海海事大学商船学院，上海 201306）

基于Lattice-Boltzmann方法的纳米颗粒多孔介质导热特性

阚安康，康利云，曹丹，王冲

（上海海事大学商船学院，上海 201306）

为研究气凝胶纳米颗粒的导热特性，提出了一种基于随机统计原理的构造气凝胶多孔介质介观尺度三维物理模型的方法。模型中颗粒空间分布、粒径分布及孔隙率可以根据实际气凝胶微尺度结构数据调整。基于所构造的物理模型，采用D3Q15LBM进行了数值模拟。分析了颗粒尺寸、孔隙率等因素对气凝胶导热性能的影响规律，即在既定孔隙率下，热导率随粒径增大而减小；既定粒径下，随孔隙率的递增热导率先下降后上升；颗粒尺寸不均匀性对热导率的影响甚大。模拟与实验结果相吻合。研究工作对优化气凝胶导热性能，提高其有效热导率的预测精度具有参考价值。

气凝胶；热导率；格子Boltzmann方法；介观尺度；物理模型

上述研究方法及物理模型多以体积平均论或构造等效物理模型为基础，为数值分析提供了有效的方法。而事实上，纳米多孔材料的微观构造非常复杂，纳米颗粒空间分布、颗粒尺寸及聚集程度都有很大的随机性。本文基于随机统计原理，提出一种气凝胶材料的三维介观物理模型的构造方法。基于所构造的介观物理模型，采用D3Q15LBM模型分析了颗粒尺寸、孔隙率等因素对纳米气凝胶颗粒多孔材料导热性能的影响。

图1　气凝胶微尺度空间结构SEM图Fig.1　Micro structure of aerogel (amplified 3000 and 50000 times)

1　物理及数学模型

1.1三维介观物理模型的建立

为研究气凝胶微尺度空间结构，对其进行了SEM扫描和图像二值化处理，扫描后图像如图1所示。由图可知，纳米二氧化硅颗粒分布无序，粒径大小不一，且有颗粒聚集成团的现象。纳米颗粒的孔隙率、颗粒尺寸等参数可以借助分析软件获取。图1中纳米颗粒的直径多集中在4～10 nm之间，颗粒呈球状。本文针对纳米多孔介质微观构造特点提出一种随机构造其三维介观物理模型的方法，具体构造流程如图2所示。

图2　气凝胶三维介观物理模型构造流程Fig.2　Generation procedure of aerogel’s three-dimensional mesoscopic physical model

图3　F均匀分布、不同cd所构造的介观物理模型Fig.3　Mesoscopic physical model with F uniform distribution and various cd(r=4 nm,ξ=0.84)

图3为分布概率。F为均匀分布，半径r=4 nm，孔隙率ξ=0.84，固相核生长率cd不同时随机构造的气凝胶纳米颗粒介观尺度模型。由图可知，cd=0.01 时[图 3(a)]对应的模型纳米颗粒最集中，大部分聚集于立方体中心，均匀性最差，cd=0.05[图 3(b)]和cd=0.5[图 3(d)]对应模型中纳米颗粒集中程度近似相同，而cd=0.1[图3(c)]时，纳米颗粒分布最为均匀。

因模型为随机生成，故可通过观察可见面上颗粒的多少来判断该模型均匀性。立方体面上颗粒越少，则该模型的颗粒越向立方体中心聚集，模型均匀性越差。在三维介观物理模型的构造过程中，由于固相核生长率cd的不同，所构造出的三维模型中气凝胶颗粒分布的均匀性也不同。其他参数相同时，cd取值在0.1附近，纳米颗粒分布较均匀；当cd<0.1且减小时，纳米颗粒分布的不均匀性增大且生成模型耗时增长；当 cd>0.1且增大时，纳米颗粒聚集程度逐渐增大。故综合考虑固相核生长率 cd对模型的影响，取 cd=0.1且分布概率服从均匀分布时所构造三维介观物理模型均匀性最佳，且表现为各向同性。

事实上，纳米颗粒尺寸并不可能是完全均匀一致的，取平均值进行构造与实际情况存在较大误差。为研究颗粒不均匀性对热导率的影响，本文选取纳米颗粒半径的最大值rmax和最小值rmin及两者数量的比例Nmax∶Nmin作为研究对象，基于本随机方法进行了介观尺度物理模型的构造。本文选取 rmax=4 nm，rmin=2 nm，分布概率 F为均匀分布，cd=0.1, ξ=0.84，随机生成的介观尺度模型如图 4所示。图中，绿色颗粒为大半径颗粒，蓝色颗粒为小半径颗粒。

1.2数学模型的建立

为精确预测材料的有效热导率，必须正确求解温度及热通量的能量运输方程。对于无对流、无辐射、无相变且无内热源的稳态纯导热问题，热量传递的控制方程可由Laplace方程表示为[5]

式中，λn为所在节点第n相的热导率；T为温度。

在两相（i和j）表面，由于受到温度及热流的连续性限制，故在相表面有

式中，int表示两相（i和j）的接触面。

为解答三维多相情况下多孔材料内部的能量运输方程，可以将能量方程表示为

式中，eα为离散格子速度；τn为节点所在相的量纲1弛豫时间。

对D3Q15LBM模型的速度分布及各参数设置如下

式中，(ρcp)n表示第n相的单位体积热容，基于共轭换热效应，不同相间的单位体积热容相等，取(ρcp)n=1，c=δx/δt表示格子声速，其值可以取任何正值，但需保证 τn的取值范围在（0.5,2）之内[3-4]。温度及热流可以根据式(8)、式(9)计算

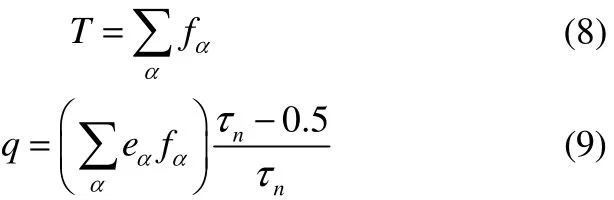
当温度演化达到平衡后，有效热导率可以表示为

式中，q为在温差ΔT驱动下，穿过长度为L,截面积为dA的稳态热通量。

1.3边界条件的处理

模拟精度很大程度上取决于计算网格划分的稀疏程度，网格划分越多，模拟结果精度越高。本文控制区域选为100×100×100的网格，格子步长设为δx=1 nm，这样可保证模拟精度，且效率高。设置热流方向上的两表面为恒温表面，其余4个侧面为绝热壁面。当研究Z方向的有效热导率时，设置Z=100及Z=0界面为恒温边界条件，温度分别为Ts及 Tx，且有 Ts>Tx，其余各侧面为绝热面。研究其他方向的有效热导率时，边界条件的设置同理。对于绝热表面，为了避免能量沿绝热表面泄漏，统一采用镜面反射；对于等温面统一采用 Zou等[19]提出的非平衡态分布反射规则

式中，α和β代表相反的两个方向，平衡态分布函数feq可由局部温度边界条件求得。

2　仿真结果及分析

根据文献[20]，空气热导率取常温下值 0.025 W·m-1·K-1，气凝胶固体基质热导率取 1.370 W·m-1·K-1。

图5　气凝胶材料有效热导率随颗粒半径的变化Fig.5　Effective thermal conductivity versus particle radius

图5为孔隙率为0.9时，气凝胶有效热导率随颗粒半径的变化关系。当气凝胶颗粒半径在 2～10 nm的范围内变化时，有效热导率在 0.025～0.018 W·m-1·K-1的范围内逐渐减小，且变化逐渐趋于平缓。

图6给出不同颗粒半径下二氧化硅气凝胶有效热导率随孔隙率的变化关系。颗粒尺寸非均匀分布时，大小球等比例混合。由图可知，随着孔隙率从0.6变化到0.97的过程中，二氧化硅气凝胶材料的有效热导率先减小后增大。分析可知，孔隙率较小时，固相导热在热量的传递过程中起主导作用，有效热导率随孔隙率增大而减小，而当孔隙率继续增大到某一值后，气相导热起主导作用，有效热导率随孔隙率的增大而增大。颗粒尺寸越不均匀，最小值出现时对应的孔隙率越小。在孔隙率确定时，有效热导率会随着颗粒尺寸的不均匀性而变化，在孔隙率较小时，颗粒尺寸越不均匀有效热导率越小，而当孔隙率增大到一定程度后，颗粒尺寸越不均匀，有效热导率越大。这表明孔隙率较小时，颗粒尺寸的不均匀性降低了气凝胶材料的导热特性；孔隙率较大时，不均匀性又使气凝胶材料导热特性增强。

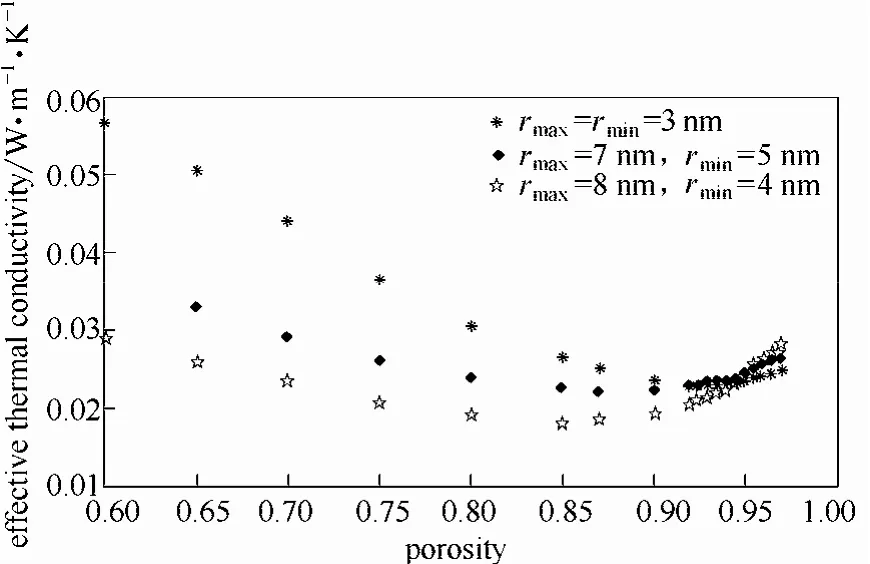
图6　不同粒径时气凝胶材料有效热导率随孔隙率的变化Fig.6　Effective thermal conductivity versus porosity with various particle sizes

3　实验对比分析

为验证本模拟结果与实际气凝胶热导率之间的一致性，定制了4组气凝胶平板，规格均为300 mm×300 mm×20 mm，并进行了实验对比研究。气凝胶材料的热导率采用大平板热保护法进行测试，测试的标准严格按照GB/T 3399—2009进行，即实验中设定热板温度为35℃,冷板温度为15℃，设定的冷热板温度值与模拟过程上下表面边界设定温度近似相等。仿真及实验结果见表 1，其对比及规律变化情况如图7所示。

表1　模拟结果与实验结果的对比Table 1　Comparison of calculated values and experimental values

图7为平均半径3 nm时气凝胶材料有效热导率随孔隙率的变化关系。由图可知，孔隙率由 0.6增大到0.97时，模拟值先减小后增大。孔隙率小于0.92时，气凝胶材料有效热导率随孔隙率的增大而减小；孔隙率大于0.92且继续增大时，气凝胶材料有效热导率有增大趋势。

由图6及表1可知，孔隙率在0.85～0.97范围内变化时，实验测量值与模拟值的变化趋势相同，且针对某一组固定的孔隙率和平均半径，误差很小。表1及图7中误差产生的主要原因如下。

（1）物理模型及模拟过程具有一定的统计随机性，虽然模拟结果是多次测量再取平均值，但这并不能完全消除随机因素的影响。

（2）纳米多孔材料内部真实的粒径分布近似正态分布，实验过程只是选取平均半径为3 nm的气凝胶样品，这并不表示所有的纳米颗粒半径都为3 nm,而模拟过程所建模型则设定所有颗粒半径都为 3 nm。事实上，实验样品纳米颗粒半径所服从正态分布的标准差越小，半径值分布越向平均值（期望值）接近，模拟与实际的误差越小。

图7　实验与仿真中有效热导率随孔隙率的变化Fig.7　Effective thermal conductivity versus porosity in simulation and experiment

4　结　论

本文提出了一种基于统计原理随机构造纳米颗粒多孔介质三维介观物理模型的方法，所构造模型的纳米颗粒空间分布、粒径分布及孔隙率可以根据构造参数进行调整，可无限接近真实结构。基于三维介观物理模型，采用D3Q15LBM模拟纳米多孔材料内部热量传递，预测了其有效热导率。结论如下。

（1）构造的三维介观物理模型能够真实地表述纳米多孔材料的微观结构信息。通过调整分布函数F及固相核生长率cd，可有效控制纳米颗粒空间分布的稀疏程度。当其他参数不变时，cd接近0.1时所构造的三维模型分布最为均匀，当cd<0.1且减小时，颗粒分布不均匀性增强，当cd>0.1且增大时，颗粒聚集程度增强，cd=0.1且F服从均匀分布时所构造模型表现为各向同性。

（2）基于F均匀分布，cd=0.1所构造的介观模型，采用D3Q15LBM模型可准确预测纳米多孔材料的有效热导率。孔隙率一定时，有效热导率随颗粒尺寸的增大而逐渐减小，且变化逐渐趋于平缓。

（3）孔隙率递增时，纳米颗粒气凝胶有效热导率先减小后增大。孔隙率较小时，颗粒尺寸的不均匀性会降低气凝胶材料的导热特性。反之，孔隙率较大，颗粒不均匀性使导热特性增强。

References

[1] Han Yafen (韩亚芬), Xia Xinlin (夏新林), Liu Haidong (刘海东). Characteristic of heat conduction in nano-insulation material [J]. Journal of Functional Materials (功能材料), 2014, 45(3): 3017-3019.

[2] Wang Moran, Wang Jinku, Pan Ning, Chen Shiyi. Mesoscopic predictions of the effective thermal conductivity for microscale random porous media [J]. Phys. Rev. E., 2007, 75(3): 036702.

[3] Wang Moran, Kang Qinjun, Pan Ning. Thermal conductivity enhancement of carbon fiber composites [J]. Applied Thermal Engineering, 2009, 29: 418-421.

[4] Wang Moran, Wang Xinmiao, Wang Jinku, Pan Ning. Grain size effects on effective thermal conductivity of porous materials with internal thermal contact resistance [J]. Journal of Porous Media, 2013, 16(11): 1043-1048.

[5] Wang Moran, Pan Ning. Predictions of effective physical properties of complex multiphase materials [J]. Material Science and Engineering R: Reports, 2008, 63(1): 1-30.

[6] Mendes M A A, Ray S, Trimis D. A simple and efficient method for the evaluation of effective thermal conductivity of open-cell foam-like structures [J]. International Journal of Heat and Mass Transfer, 2013, 66: 412-422.

[7] Talukdar P, Mendes M A A, Parida R K, Trimis D, et al. Modeling of conduction-radiation in a porous medium with blocked-off region approach [J]. Int. J. Therm. Sci., 2013, 72: 102-114.

[8] Kwon Jae-Sung, Jang Choong Hyo, Jung Haeyong, Song Tae-Ho. Effective thermal conductivity of various filling materials for vacuum insulation panels [J]. International Journal of Heat and Mass Transfer, 2009, 52(23/24): 5525-5532.

[9] Ma Yongting, Yu Boming, Zhang Duanming, Zou Mingqing. A self-similarity model for effective thermal conductivity of porous media [J]. Journal of Physics D: Applied Physics, 2003, 36(17): 2157-2164.

[10] Yu Boming, Li Jianhua. Some fractal characters of porous media fractal [J]. Fractals, 2001, 9(3): 365-372.

[11] Dathe A, Thullner M. The relationship between fractal properties of solid matrix and pore space in porous media [J]. Geoderma, 2005, 129: 279-290.

[12] Kan Ankang (阚安康), Zhang Tingting (张婷婷), Cao Dan (曹丹). Vacuum thermal conduction characteristic of nano-granule porous medium using fractal theory [J]. CIESC Journal (化工学报), 2013, 64(11): 4008-4014.

[13] Kan Ankang (阚安康), Zhang Tingting (张婷婷), Lou Haijun (楼海军). Fractal study of effective thermal conductivity of fiber glass materials [J]. Journal of Vacuum Science and Technology (真空科学与技术学报), 2013, 33(7): 654-660.

[14] Ma Qiang (马强), Chen Jun (陈俊), Chen Zhenqian (陈振乾). Lattice Boltzmann simulation for heat and mass transfer in fractal porous media [J]. CIESC Journal (化工学报), 2014,65(S1):180-187.

[15] Di Xiaobo, Gao Yimin, Bao Chonggao, Hu Yongnian, Xie Zhengang. Optimization of glass fiber based core materials for vacuum insulation panels with laminated aluminum foils as envelopes [J]. Vacuum, 2013, 97: 55-59.

[16] Di Xiaobo, Gao Yimin, Bao Chonggao, Ma Shengqiang. State thermal insulation property and service life of vacuum insulation panels with glass fiber chopped strand as core materials [J]. Energy and Buildings, 2014, 73:176-183.

[17] Simmler H, Brunner S. Vacuum insulation panels for building application: basic properties, aging mechanisms and service life [J]. Energy and Buildings, 2005, 37(11): 1122-1131.

[18] Li Renmin (李仁民), Liu Songyu (刘松玉), Fang Lei (方磊), Du Yanjun (杜延军). Micro-structure of clay generated by quartet structure generation set [J]. Journal of Zhejiang University: Engineering Science Edition (浙江大学学报：工学版), 2010, 44(10): 1897-1901.

[19] Zou Qisu, He Xiaoyi. On pressure and velocity boundary conditions for the lattice Boltzmann BGK mode [J]. Physics of Fluids, 1997, 9(6): 1591-1598.

[20] Shi Ling (石零). Investigation of heat transport on the solid-solid contact interface at low temperature [D]. Wuhan: Huazhong University of Science and Technology, 2006.

Thermal conduction characteristic of nano-granule porous material using lattice-Boltzmann method

KAN Ankang, KANG Liyun, CAO Dan, WANG Chong
(Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China)

To study the thermal property of silica aerogel, a method is proposed for constructing three-dimensional mesoscopic physical model of nanoparticle porous materials, based on the random statistical theory. The spatial distribution of particles, particle size and porosity can be adjusted according to actual microscopic information of the porous material. D3Q15LBM model is employed to perform numerical simulation and analysis in mesoscopic scale. And the influence of particle diameter, porosity and other factors on thermal conductivity of porous media is analyzed. That is, the thermal conductivity will decrease with the increase of particle size for constant porosity; the thermal conductivity falls and then rises as the porosity increases for constant particle size; the uniformity of particle size plays an important role on the thermal property. The simulation results are nearly the same with the experimental ones. The research will be an excellent reference for optimization of thermal performance and prediction of effective thermal conductivity for aerogels.

aerogel; thermal conductivity; lattice-Boltzmann method; mesoscopic scale; physical model

引　言

气凝胶为二氧化硅纳米颗粒固体基质及颗粒之间空隙填充的空气组成的一种多孔介质保温材料[1]，因其高孔隙率、高比表面积、低热导率等优点而被需保温系统所青睐，并得以在工程领域广为应用。热导率为衡量保温材料热工性能优劣的重要物性参数，确定保温材料的有效热导率已成为研究绝热材料的重点方向[2]。但气凝胶内部纳米颗粒的随机性和多样性使得对其内部构造的描述极其困难。通过理论分析或数值简化的方式，建立一种精度较高、通用性好的模型，对分析气凝胶物性参数对其热工性能的影响机理尤为重要。Wang等[2-5]、Mendes等[6-7]采用随机生成的方式建立了微观结构多孔介质模型，并提出了估算有效热导率的方法。Kwon等[8]基于“平均体积法”对常用的泡沫、颗粒、纤维、丝网等多孔介质芯材分别进行了分析，对固体基质、气体成分和热辐射耦合的等效热导率进行了描述，并建立了相应的物理模型及数值耦合模型。很多学者[9-14]研究发现多孔介质在连续空间中表现为“分形”特性，建立了诸多预测热导率的分形模型。Di等[15-16]、Simmler等[17]则在基于实验研究的基础上，给出了多孔介质热导率经验公式，并通过实验的方法验证了经验公式的正确性。李仁民等[18]基于Wang等[2]的Lattice-Boltzmann方法，采用四参数法对黏土微观结构进行了构造，并理论分析了其物性参数对微观结构相似性的影响。

date: 2015-04-27.

KAN Ankang, ankang0537@126.com

supported by the Natural Science Foundation of Shanghai (15ZR1419900).

10.11949/j.issn.0438-1157.20150532

TK 121

A

0438—1157（2015）11—4412—06

2015-04-27收到初稿，2015-07-08收到修改稿。

联系人及第一作者：阚安康(1981—)，男，博士，高级工程师。

上海市自然科学基金项目(15ZR1419900)。