一种ELM神经网络结构设计方法及在卫星钟差预报中的应用1

雷雨，郭浩

一种ELM神经网络结构设计方法及在卫星钟差预报中的应用1

雷雨1，2，3，郭浩4

（1.中国科学院 国家授时中心，西安 710600；2.中国科学院 时间频率基准重点实验室，西安 710600；3.中国科学院大学，北京 100049；4.西安文理学院 机械与材料工程学院，西安710061）

针对极端学习机（extreme learning machine，ELM）神经网络隐层结构难以确定的问题，基于自适应共振理论（adaptive resonance theory，ART）网络良好的自组织分类功能，提出一种基于ART网络思想的ELM网络结构设计方法。该方法将ART网络的自组织聚类特性用于ELM网络结构设计中，通过对输入向量与已存模式的相似度比较将输入向量进行分类，确定隐层节点规模。仿真实验表明，与其他网络相比，ART-ELM网络具有更精简的结构、更快的学习速度以及更好的映射能力。通过用于GPS卫星钟差预报的实验表明，根据ART-ELM网络所预报的钟差较IGS超快速预报（IGS ultra-predicted，IGU-P）钟差在精度上有较大改善。

极端学习机；网络结构设计；自适应共振理论网络；钟差预报

0　引言

极端学习机（extremelearningmachine，ELM）是近年发展起来的一种新型单隐层前馈神经网络[1]，因其具有结构简单、学习速度快和泛化能力好等优点，目前在时间序列预测等领域得到了广泛应用[2-3]。ELM的网络结构为3层，包括1个输入层、1个输出层和1个隐层，其中隐层包含大量的非线性节点。ELM克服了传统前馈神经网络收敛速度慢、容易陷入局部最优等缺陷，在训练初始阶段随机产生输入权值和偏置，并在训练过程中保持不变，其网络的输出权值是唯一需要确定的参数。

已有研究表明，ELM的学习和泛化能力在很大程度上取决于隐层节点数量[1]，所以在设计ELM网络时，如何确定最优的网络结构一直都是研究的重点。许多学者就ELM网络的结构设计问题展开了研究，试图寻求一种合适的方法来确定ELM网络的隐层节点个数，其中剪枝算法是前馈神经网络结构设计的一种有效方法[4-5]，该类算法首先构造一个足够大的网络，然后通过训练删除或合并某些节点或权值，实现设计紧凑网络结构的目的。Y.Miche等[5]基于剪枝思想提出了最优剪枝极端学习机（optimally pruned ELM，OP-ELM），该算法首先利用ELM算法建立一个规模较大的网络，然后利用多响应稀疏回归算法对隐层节点排序，最后通过留一准则对隐层节点进行删除。OP-ELM算法能有效精简网络规模，但计算过程较为复杂。

自适应共振理论（adaptiveresonancetheory，ART）网络是基于生物机制建立的人工神经网络，具有自组织聚类分析的功能，能对相同特征的事物进行自组织分类[6]。当有新的模式进入网络时，会与已有模式进行对比，如果新模式与已有的一类模式相似度高时，则可以归为既有的一类；如果新模式与已有模式不相似，则需要在网络中建立一个新的模式类。当对所有样本比较结束后即完成模式分类。基于此，有学者基于ART神经网络的聚类特性来设计径向基函数（radial basis function，RBF）神经网络的隐层节点[7-8]。因为ELM网络隐层节点的确定也可以转化为聚类问题，故本文提出了一种新的基于ART思想的ELM网络结构设计方法。利用ART的分类思想，通过一次相似度比较来自动确定ELM网络的隐层节点个数，仿真实验表明，基于本文思想所设计的网络结构，与其他网络相比，不仅结构简单，而且泛化能力好、学习速度快。最后将ART-ELM算法用于GPS卫星钟差预报，结果表明，通过该算法得到的预报钟差较IGS超快速预报（IGS ultra-predicted，IGU-P）钟差在精度上有较大改善。

1　ELM算法

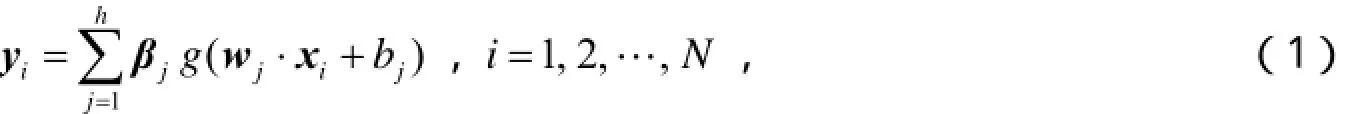
式（2）至（3）中，H为隐层输出矩阵。

ELM算法的具体步骤如下[1]：①随机选取输入层权值wj和偏置bj，j=1，2，…，h ，并保持不变；②计算隐层输出矩阵H；③计算输出权值β=H†Y，其中H†为矩阵H的Moore-Penrose逆。

2　基于ART的ELM网络结构设计

对ELM网络结构的设计即为对隐层节点个数的确定，这个问题可以转化为聚类问题，即寻求一种合适的聚类算法来确定隐层节点的规模，本文利用ART网络的自组织分类功能来确定ELM网络隐层节点的规模。

基于聚类算法的ELM网络通过对向量进行相似度比较来完成分类，相似度公式为[9]

即第j*个隐节点与第i个输入向量的相似度最大。下面分两种情况进行讨论：

式（7）中，V为警戒参数，可以控制网络的分类力度，V值越大，分类精度越高。

综上，基于ART的ELM网络结构设计算法如下：①将网络隐层节点个数初始化为0；②当第1个样本进入网络后，为网络分配1个隐层节点，并令；③当第i个样本进入网络后，计算第i个样本的输入向量与现有所有隐层节点中心向量的相似度，并找出与第i个输入向量相似度最大的隐层节点j*；④若满足隐层节点增加准则，则为网络增加1个隐层节点，并将第i个输入向量赋予新的隐层节点作为其中心向量，如式（9）所示，转向③；否则转至⑤；⑤按式（7）对第 j*个隐层节点的中心向量进行调整，转向③。

3　仿真实验

为了检验基于ART的自组织ELM网络的非线性映射能力，对典型的非线性函数sinE进行逼近，sinE函数为

随机选取300个样本对网络进行训练，400个样本对网络进行测试，警戒参数设定为0.8，激活函数选用Sigmoid函数，其表达式为函数逼近效果如图1所示。由图1可以看出，ART-ELM网络经过学习训练后能够很好地逼近非线性函数sinE，期望输出曲线与实际输出曲线基本能达到重合，说明基于ART的自组织ELM网络具有较强的非线性映射能力。

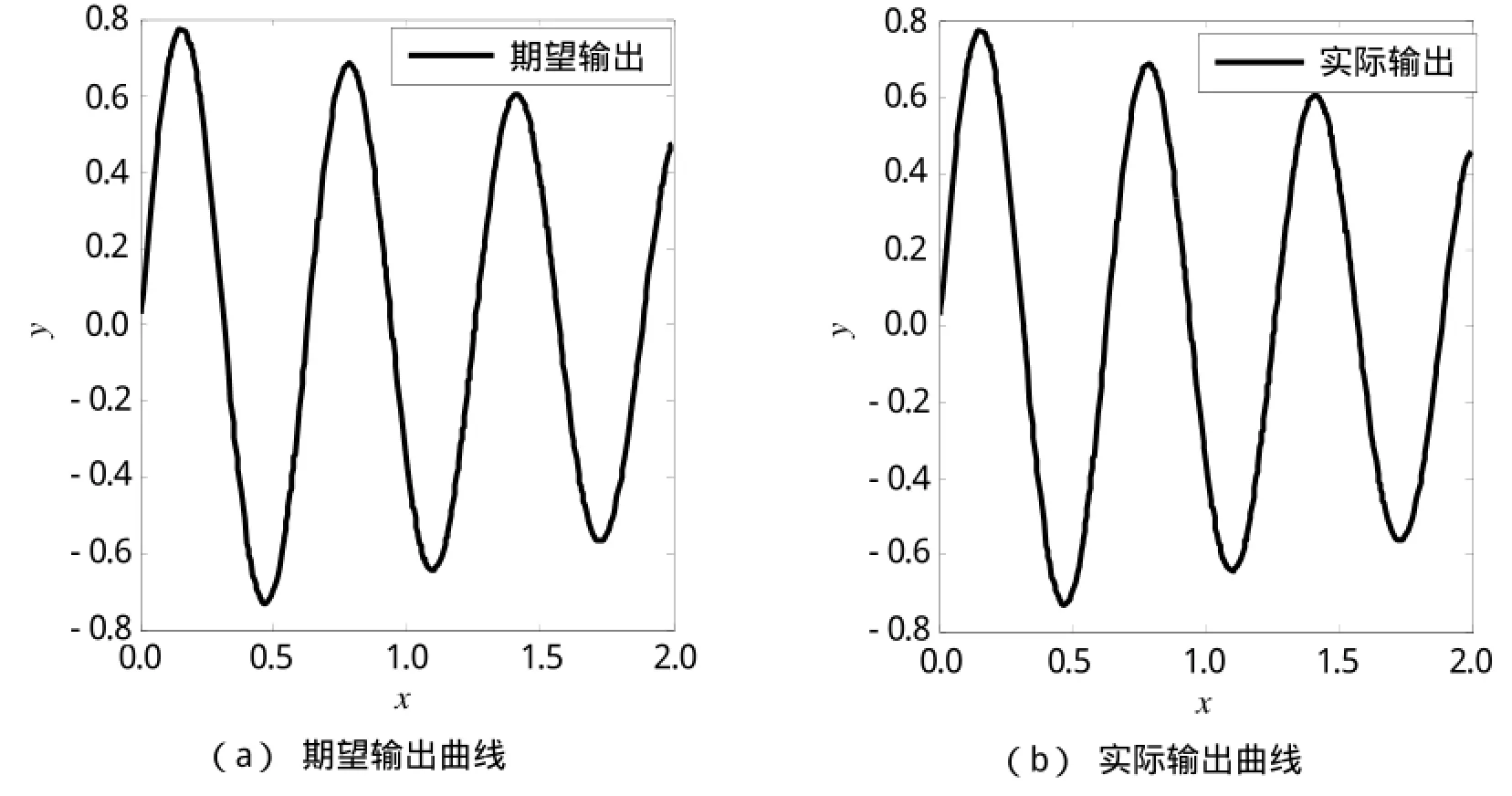
图1　函数逼近效果

为了进一步验证所提方法的有效性，将ART-ELM网络的函数逼近效果与其他算法进行对比，比较结果如表1所示。实验环境为Intel Core™I7 CPU，主频1.73 GHz，8.00 GB内存，Microsoft Windows 7操作系统（64位），MATLAB R2013a软件平台。仿真实验中采用的网络性能评价指标包括程序运行100次的平均均方根误差（RMSE）和训练时间。

由表1可知，与其他网络结构相比，本文提出的ART-ELM网络隐层结构更为精简，隐层节点规模要小于其他网络，此外，ART-ELM网络不仅学习速度较快，并且测试误差较小，泛化能力优于其他网络。

表1　函数逼近效果对比

4　ART-ELM网络在GPS卫星钟差预报中的应用

卫星钟差是导航卫星精密定位的主要误差源之一。以GPS为例，目前IGS发布的事后精密卫星钟差精度最高可达75ps，但实时性不足，而满足实时性的广播星历钟差和IGU-P钟差精度却不理想。因此，提高卫星钟差预报精度是非常必要的。我们在文献[2]和文献[10]中将ELM神经网络和广义回归神经网络用于GPS卫星钟差预报中，研究表明神经网络技术用于卫星钟差预报可以取得较好的预报效果。本文将ART-ELM网络用于GPS卫星钟差预报，以改善IGU-P钟差产品的质量，在实验中警戒参数仍设定为0.8。

采用2011年10月30日IGS提供的15 min采样间隔的超快速观测（IGS ultra-rapidobserved，IGU-O）钟差作为建模数据，预报随后1d的钟差，以预报时刻所对应的IGU-O钟差产品作为参考值，使用RMSE、最大误差与最小误差之差的绝对值（这里称为误差变化范围（Range））作为统计量来评价预报结果的精度和算法的稳定性，并将其与IGU-P钟差产品进行比较。在建模阶段，按照表2所示方式构造训练样本，其中L为建模数据序列长度，m为输入向量维数，视不同卫星而定。在预报阶段，令作为输入向量（ΔX为观测钟差），获得序列的一步预测值，然后令，得到新时间序列作为下一时刻的输入向量，以此类推，即可实现钟差的多步预报。需要说明的是，在对网络进行训练之前，需要对训练样本进行预处理，这里采用一阶差分的方法，而在预报阶段，须对网络输出进行反变换，以获得最终的钟差预报值。

表2　训练样本的构造方式

图2和表3给出了PRN09、PRN10、PRN14和PRN15 4颗卫星的钟差预报对比情况（限于篇幅，这里仅以4颗卫星为例进行说明，其他卫星亦可，其中这几颗星载钟包括BlockⅡA Cs钟、BlockⅡA Rb钟、BlockⅡR Rb钟以及BlockⅡR-MRb钟4类）。为了验证神经网络相对于线性模型的优越性，本文还给出了ART-ELM网络同二次多项式（quadratic polynomial，QP）模型和灰色模型（GM（1，1））的对比结果，其中使用2011年10月30日1d的数据建立QP模型，使用该天最后2 h的数据建立灰色模型。

由图2和表3可知：

①GPS星载Rb钟的预报精度和预报稳定性明显好于星载Cs钟，这是由于携带Cs钟的BlockⅡA卫星为GPS早期发射的，由于设备老化以及Cs钟本身物理特性等因素的综合影响使Cs钟的可预测性相对较差。

②预报精度方面，ART-ELM网络的预报结果明显高于IGU-P产品，24h的钟差预测RMSE最大改进了74.78%。同时本文所建模型的预报精度高于2种常用模型，即使对于可预测性较差的星载Cs钟，ART-ELM网络也具有相对较好的预测效果。

③预报稳定性方面，对于提前12h的预报，本文所提方法的预报结果与IGU-P产品基本相当，但随着预报时长的增大，IGU-P产品的预报误差表现出发散趋势，预报稳定性有一定程度的降低，而2种常用模型的预报稳定性则随着卫星的不同而变化，稳定性相对较差。

本文利用IGU-O钟差数据作为训练样本，训练时间很短，其训练时间和预报时间之和一般在1 min以内，保证了算法的实时性。

图2　4颗卫星1 d钟差预报误差对比图

表3　4颗卫星预报误差统计　ns

5　结语

将基于生物机制建立的ART网络用于ELM网络结构设计中，利用ART的自组织聚类特性自适应调整隐层节点个数，构造样本驱动的自适应ELM网络。通过对典型非线性函数sinE的逼近，表明了基于ART机制建立的ELM网络与其他网络相比，结构更精简、学习速度更快、非线性映射能力更强。最后，将ART-ELM网络用于GPS卫星钟差预报实际问题中，实验表明所建钟差模型能够以较高的精度和相对稳定的性能来预报卫星钟差数据，预测效果明显好于传统二次多项式模型和灰色模型，其预报得到的钟差相比于IGU-P钟差在精度上有较大改善，同时所建模型简单且具有较好的实时性。因此，可以考虑作为一种新型的卫星钟差预报方法使用。

[1]HUANG Guang-bin,ZHU Qin-yu,SIEW C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006, 70(1):489-501.

[2]雷雨,赵丹宁.极限学习机在卫星钟差预报中的应用[J].大地测量与地球动力学,2013,33(5):53-57.

[3]LEI Yu,ZHAO Dan-ning,CAI Hong-bin.Extreme learning machine for the predictions of length of day[J].Aritificial Satellites, 2015,50(1):19-33.

[4]RONGJian-hua,ONGY S,TANA H,etal.A fastpruned-extremelearningmachineforclassificationproblem[J].Neurocomputing, 2008,72(13):359-366.

[5]MICHE Y,SORJAMAA A,BAS P,et al.OP-ELM:optimally pruned extreme learning machine[J].IEEE Trans on Neural Networks,2010,21(1):158-162.

[6]CARPENTER G A,GROSSBERG S.The ART of adaptive pattern recognition by a self-organizing neural network[J].IEEE Computer,1988,21(3):77-88.

[7]LEE S J,HOU Chun-lin.An ART-based construction of RBF networks[J].IEEE Trans on Neural Networks,2002,13(6): 1308-1321.

[8]蒙西,乔俊飞,韩红桂.基于ART的RBF网络结构设计[J].控制与决策,2014,29(10):1876-1880.

[9]FU Li-min,YANG M,BRAYLAN R,et al.Real-time adaptive clustering of flowcytometric data[J].Pattern Recognition,1993, 26(2):365-373.

[10]雷雨,赵丹宁,高玉平.基于灰色系统和神经网络的钟差预报[J].时间频率学报,2013,36(3):156-163.

Anetwork structure design method for ELM and its application to prediction of satellite clock bias

LEI Yu1，2，3，GUO Hao4
（1.National Time Service Center，ChineseAcademy of Sciences，Xi′an 710600，China；2.Key Laboratory of Time and Frequency Primary Standards，National Time Service Center，ChineseAcademy of Sciences，Xi′an 710600，China；3.University of ChineseAcademy of Sciences，Beijing 100049，China；4.Mechanism and Material Engineering College，Xi′an University，Xi′an 710061，China）

It is difficult to determine the hidden layer structure of an extreme learning machine（ELM）.In this paper，a new method for design of ELM hidden layer structure is proposed based on the self-organizing classification characteristics of adaptive resonance theory（ART）neural network.The proposed method employs the clustering property of ART network to design the ELM network structure.The number of hidden layer nodes can be determined adaptively through the similarity comparison of input vector.The simulation result shows thatthe ART-ELM network is characteristic of more concise network structure，faster learning speed and better generalization ability compared to other neural networks.Finally，the ART-ELM network is applied to prediction of GPS satellite clock bias.The experiment result indicates that the proposed algorithm outperforms the IGS ultra-predicted（IGU-P）solution in precision of clock bias prediction.

extreme learning machine（ELM）；network structure design；adaptive resonance theory（ART）network；clock bias prediction

P227

A

1674-0637（2015）04-0209-07

10.13875/j.issn.1674-0637.2015-04-0209-07

2015-05-18

国家自然科学基金资助项目（11503031）

雷雨，男，博士，助理研究员，主要从事地球自转变化监测与预报研究。