初中数学命题联想系统的实践与探讨

陈智慧

摘 要：在初中数学学习中建立起一个有效的命题联想系统，对解决所遇到的数学问题能起到事半功倍的作用。构建基础知识网络、启动联想思维，搭建数学的认知结构、形成对某类数学问题的解决方法，是创造命题联想系统的必要条件。

关键词：基础知识网络;联想思维;认知结构;命题联想系统

在数学学习过程中，好多学生遇到具有创造性的数学题目时，都要经过一番冥思苦想后，才能“豁然开朗”。但在日常的传统教学中，面对这样的情况往往只能靠自己意会，而不能言传。本文将对不能用语言传授的这类数学问题进行重新认识，用非正常的逻辑思维形式----数学联想思维。重点对数学联想思维在中学数学中的实践以及中学数学联想思维认知结构的搭建最终形成命题联想系统进行简单的探讨。

一、运用联想思维解决几何问题

几何题的证明一般是从结论倒过来找条件的，然而从题目中已知条件就能很快看出并反馈很多存在的信息（性质，解决方法）是极具价值的，即构建命题系统是至关重要的。脑子里关于某个定理，某个已知条件，某个图形的关联性质越多，而且这些关联性质涉及的知识面越宽、越广，尤其是别人注意不到的，那么在推理证明时，他就能够更快、更好地找到已知条件和要证明的结论间的联系，乃至构建条件和结论间“神奇”的纽带，从而找到证明结论的关键所在。

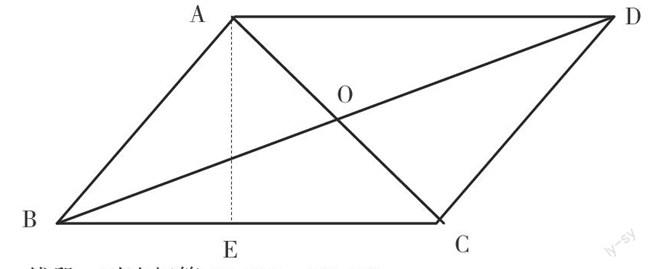
例如，在平行四边形ABCD中，对角线交点为O，那么可以得到：

线段：对边相等AB=CD，AD=BC;

对角线互相平分：AO=CO，BO=DO;

直线位置关系：AB∥CD，AD∥BC

周长：C=2（AB+BC）

面积：S=BC×AE

角：對角相等∠ABC=∠ADC，∠BAD=∠BCD;

对顶角相等∠AOB=∠COD，∠BOC=∠AOD;

内错角相等∠ADB=∠DBC，∠DAC=∠ACB，

∠BAC=∠ACD，∠ABD=∠BDC;

同旁内角互补∠DAB+∠ABC=180°，∠ADC+∠DCB=180°，

∠ABC+∠BCD=180°，∠BAD+∠ADC=180°

内角和等于360°

各三角形的内角和等于180°;

全等三角形：△ABO≌△CDO，△BCO≌△DAO，

△ABD≌△CDB，△ABC≌△CDA

等积三角形：除上述全等三角形是等积三角形外，还有 S△ABC=S△BCD=S△ABD=S△ACD

对于以上相关性质的掌握是多多益善，并且特别要注重，性质所涉及的知识领域越多越好。经常有这样的情况，记得上面的三角形全等的性质，就是想不起等积三角形的性质;而对某个方面的性质，只要提起一个，其他的性质就能全部联想起来。能否记得性质所涉及的“知识领域”，即是反映出了掌握命题的“宽度”。

二、运用联想思维解决函数问题

在函数问题的解决中，好多学生往往是习惯于一种定向思维的表述方式，而换种方式表述同样的意思就不知所措，甚至还会把题意理解错误。原因在于没有练就扎实的基本功，没掌握所涉及领域的数学基础知识，在头脑里未形成相关知识的信息网络体系。万变不离其宗，只要具备自己的相关数学基础知识网络体系，构建了解决相应问题的结构方式，启动灵活善变的思维，问题的关键结点想逃出你的掌控也是确实不易的。

例如：在讲解“直线y=kx+3过点A（1，2）”时，可以转换“点A（1，2）在直线y=kx+3上”，进一步转换成“点A（1，2）的坐标x=1，y=2适合方程”，这三种说法也是等价的，组成一个等价命题系统。按照最后的说法，把x=1，y=2代入方程，就可以求出K，从而就可以确定直线方程了。

譬如：前面说到的“直线y=kx+3过点A（1，2）”和“点A（1，2）在直线y=kx+3上”，涉及的对象没有变化，仍然是直线y=kx+3和点A（1，2），只是表述的主体从直线转换为了点。另一种是表述的对象发生了变化，这时，“问题系统”也随之发生了变化。如“x=1，y=2适合方程y=kx+3”已经不是几何问题了，而是代数问题了。

三、应用联想思维解决代数问题

例如：“3xm+5y2与x3yn的和是单项式”时，可以转换为“3xm+5y2与x3yn可以合并”，也可以表述为“3xm+5y2与x3yn是同类项”。前两种表述考查单项式与单项式的加减运算，第三种表述的知识点为这两个单项式是同类项。具有同类项的性质，即相同字母的指数相同，从而可求出m，n的具体数值。

通过以上的实践应用可以看出，在解决数学问题的思维活动过程中，联想能沟通数学对象与关联知识之间的联系。基本的联想思维是人们在认知事物的过程中，依据事物内在的某种因素，从一件事物联想到其它事物的心理活动过程。它就是一种由此及彼的思维过程活动。联想思维在认知活动过程中起到了桥梁和纽带的作用。针对某些未知的数学知识点，由已知知识点与未知知识点的联系，使得某些未知知识点的数学问题得到解答。针对具体的数学题解答过程中，通过对题目上已给出的条件、图形特征及所求目标进行分析，从中联想到相关已知条件的定义、定理、性质、法则等，最后找出解答题目的思路和方法。因此，在数学问题的解决中应多对用心考虑一下，题中所给已知条件、图形给我们提供了些什么信息？可以有怎么样的变形和处理方式？……。

总之，解决数学问题常常是个转化、变换的过程，从已知的A联想到B，再由B联想到C，依次类推……。利用联想思维通过层层联想，把两个或两个以上命题按一定的需要联系起来，在自己的脑子里构建出一个基础知识网络体系，从而找到解决某类数学问题的结构方式，就能形成了一个有效的数学认知结构----命题联想系统。通常有如下几类：

1.等价命题系统。就是由同一命题变换表述方式后形成的命题集。

2.下游命题系统。已知A命题，从而推理出B命题，这时我们把B命题叫做A命题的“下游命题”，由A命题可以推理出的所有命题，就形成了A命题的下游命题系统。

3.上游命题系统。为了推理出A命题，去寻找B命题，即可以由B命题推理出A命题，通常把B命题叫做A命题的“上游命题”，假如B，C，D……命题都能推理出A命题，那么以上这些命题就形成了A命题的上游命题系统。

综上所述，数学命题联想系统就好比一个计算机网络系统，数学基础知识是网络中的各个信息点，联想思维及知识跨度是网络中的各个地址链接，某类数学问题的解决方法是网络中的各个调用模块。只有具备了宽广的数学基础知识领域，再加上掌握了一定的数学知识跨度链接，就能建立起一张有效的数学基础知识网络。积极地启动联想思维，捕捉相关信息，映射出更多的相互之间的关联知识，找出针对某类数学问题的解决方法，就能搭建出一个有效的数学知识结构，从而创造出有效的数学命题联想系统。只要能在初中数学学习中建立起一个强大而有效的命题联想系统，对所遇到的数学问题，经过“系统扫描”就能迎刃而解，起到事半功倍的作用。