多波束卫星系统中低复杂度分组预编码算法
2015-09-03赵旦峰
王 杨,赵旦峰,廖 希
(哈尔滨工程大学信息与通信工程学院,150001哈尔滨)
多波束卫星系统是实现高吞吐量卫星通信的一种重要方案,可以通过频率复用提高频带利用率.全频率复用多波束卫星系统可以看作分布式MIMO系统,从而借鉴MIMO预编码以及检测技术抑制波束间同频干扰[1-2].本文研究多波束卫星系统前向链路预编码技术.
文献[3-7]研究低复杂度的迫零和最小均方误差线性预编码方案在不同结构的多波束卫星系统中的性能.文献[8-9]将非线性tomlinsonharashima预编码(THP)方案用于多波束卫星系统,能够获得比线性预编码方案更好的误码性能,但同时增加了系统复杂度.格基约减辅助的THP(lattice reduction aided THP,LRA-THP)方案利用格基约减技术,能够进一步提高系统性能,但格基约减技术的引入使预编码方案的复杂度变得更高[10].文献[11]针对多用户MIMO系统提出一种基于信漏噪比(signal-to-leakage-plus-noise ratio,SLNR)的分组预编码方案,能够获得接近LRATHP的性能,同时降低系统复杂度.该分组预编码方案同样能够用于多波束卫星系统中,降低LRA-THP的复杂度.但由于多波束卫星系统中需要联合处理的点波束很多,因此采用该分组预编码方案时,系统复杂度依然很高.
卫星通信系统中,通信卫星能量、硬件资源严格受限,因此降低预编码算法复杂度有利于预编码技术在多波束卫星通信中的应用.本文在文献[11]中分组预编码方案的基础上,针对多波束卫星系统提出一种低复杂度分组预编码方案.该方案充分利用多波束卫星信道的特点,降低预编码算法的复杂度.
文中diag{x1,…xN}为由xi构成的对角阵;(·)T和(·)H分别为转置和共轭转置;0为全零矩阵;[A]i,j为矩阵A中第i行,第j列的元素.
1 多波束卫星系统模型
考虑固定多波束卫星系统前向链路.多波束天线在地面形成的一簇K个波束如图1所示,所有波束均占用相同的频带.系统采用TDMA技术,每个时隙从各个波束选择一个用户进行数据传输.假设用户在波束内均匀分布,图1中的圆圈为一组随机的用户位置.每个用户终端包含1个天线,在一个符号周期内发送给第k个用户的数据符号为zk,且分配给每个用户的功率相等,则用户k的接收信号为

式中T为归一化预编码矩阵,使发送信号满足功率约束条件,即E{zΗTHTz}=K;z=[z1,…zK]T为原始发送符号向量;hk=[hk1,…,hkK]为第k个用户与不同波束间信道的衰落因子.nk表示方差为σ2n的高斯白噪声.
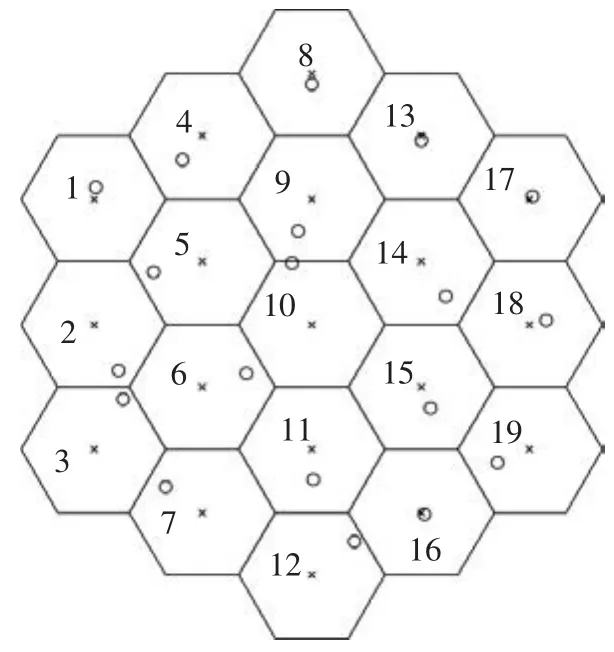
图1 多波束卫星系统一簇波束示意
联合考虑所有用户的接收信号,则y=[y1,…,yK]T可为
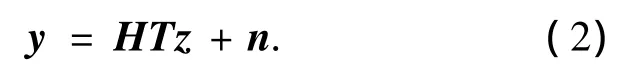
固定多波束卫星信道需要考虑路径传播损耗、多波束天线增益以及雨衰[5].天线增益由天线辐射方向图和用户位置决定.第j个波束在用户i处的辐射增益bij可用式(3)表示,图2给出一个波束的辐射方向图.

图2 单个波束的辐射方向(θ3dB=0.3)

式中:θij为第i个用户通过卫星与第j个波束中心的夹角,θ3dB为半功率波束宽度的一半,bmax=为路径传播损耗,λ和d0分别为波长和卫星轨道高度,J1和J3为第一类1阶和3阶贝塞尔函数.
降雨衰落ξdB=20log10(ξ)可以建模为对数正太分布的随机变量[5],即 ln(ξdB)~N(μ,σ2),其中μ和σ2为对应正太分布的均值和方差.由于卫星多波束天线馈源间距远小于信号传播距离,因此假设不同波束与同一个用户间的降雨衰落因子相同为第k个用户的降雨衰落因子,则信道矩阵H为
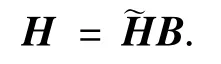
2 分组预编码算法
该小节简单介绍文献[11]中提出的分组预编码算法.图3给出了该预编码算法的结构框图.该算法将K个用户分为N组,其中第i组的用户数为gi,预编码矩阵Ti=βWiFi.β为归一化因子,用于保证发送信号满足功率约束条件.Wi用来抑制第i组用户信号到第1,…,i-1组的泄露,是通过最大化SSLNR(successive SLNR)得到的预处理矩阵.第i组用户对应的SSLNR定义为
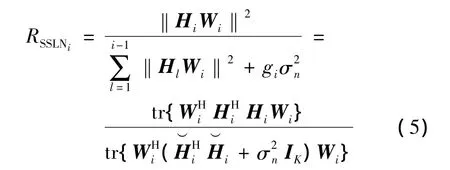
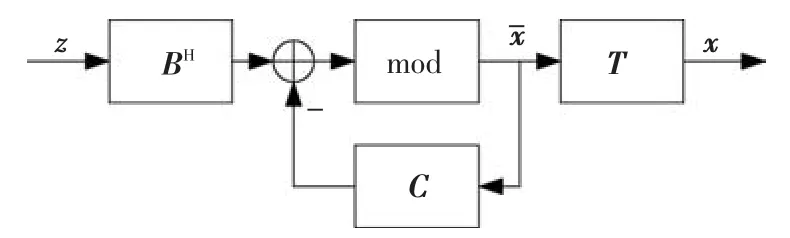
图3 分组预编码算法结构框图
最大化RSSLNi的Wi存在闭合表达形式

得到预处理矩阵Wi(i=1,…,N)后,对各组用户对应的等效信道矩阵(HiWi)H进行格基约减运算,可得
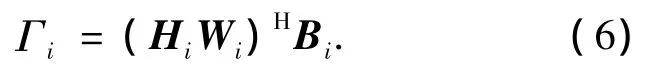
式中Bi为幺模转换矩阵,对Γi进行QR分解


最后,得到B=diag{B1,…,BN};C为子矩阵Cij构成的下三角阵;T=[T1,…,TN].
计算Wi需要进行广义特征分解.对n维矩阵束(A,B)的广义特征分解需要的浮点运算量为14n3[13].因此计算Wi的运算量为14K3.当K较大时,算法运算复杂度很高.
3 低复杂度分组预编码算法
3.1 算法原理
在文献[11]中分组预编码算法的基础上,提出一种基于SLNR的低复杂度分组预编码算法,充分利用多波束卫星信道的特点,减小需要求解的预编码矩阵的维度,从而减小广义特征分解以及矩阵乘法中矩阵的维度,降低算法的运算量.
多波束卫星系统中,由于每个波束天线辐射存在指向性,因此相距很远的两个波束间的影响很小.以图1中波束2和波束18为例,假设各个波束的辐射方向图如图2所示.波束2中的用户距波束18中心的最小距离为5倍波束半径,可得θ2,18≥ 1.5,则归一化的信道衰落因子2,18≤2.3×10-3ξ1e-jφ1.另外,波束2 中的用户与该波束间的信道衰落因子2,2≥ 0.7ξ1e-jφ1.波束 2 中用户接收到的来自波束18和波束2的信号功率之比为

可见,波束18中发送的信号对波束2中的用户影响很小,用户接收信号能量主要来自距用户较近的波束.本文提出的算法将充分利用这一特点降低预编码算法的复杂度.
假设对K个用户按如下方式进行分组

则第1组用户的接收信号
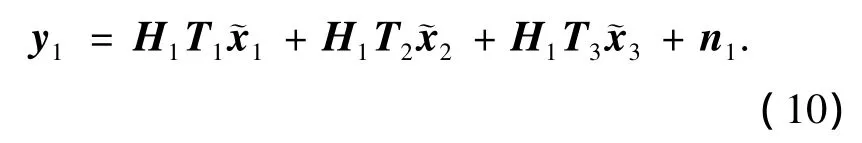
等式右侧第一项为有用信号.令H1=[H11,H12],其中H11为g1×(K-r1)的子矩阵;H12为g1×r1的子矩阵.将有用信号项展开

由对信道特点的分析可得,适当选择r1的值,可以使 ‖H12‖2/‖H11‖2≪1,此时式(11)中第二项提供的增益远小于第一项提供的增益.因此,为降低求解预编码矩阵的复杂度,考虑令T21=0,即预编码时有r1个波束不发送该组用户数据.
式(5)变为
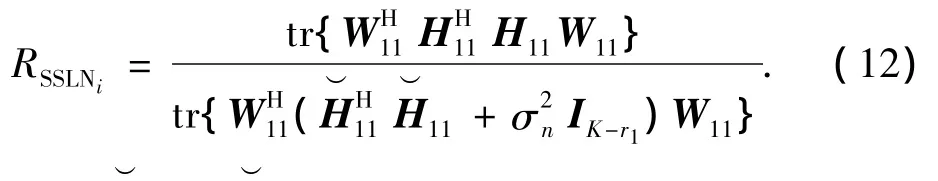
式中H11是H1的前K-r1列构成的子矩阵.最优解可以通过对矩阵束进行广义特征分解得到,运算复杂度降低为14(K-r1)3.利用相同的原理也可以减小求解W2和W3时的运算量.
得到预处理矩阵Wi(i=1,2,3)后,由式(6)~(9)可以得到B、C和T.由于Wi(i=1,2,3)中包含全零的子矩阵,因此式(6)、(9)中的矩阵乘法的运算量同样可以降低.
为分析预编码矩阵维度的降低对算法性能的影响,本文定义用户平均信干噪比

由 Rayleigh-Ritz定理[11],可得:
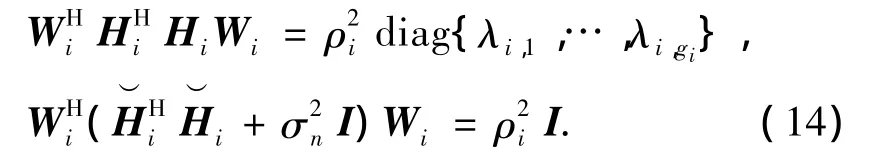
式中λi,1,…,λi,gi为Wi中广义特征向量对应的gi个广义特征值.令由于Fi为列正交矩阵且发送功率已进行归一化,因此在高信噪比条件下RSIN可近似为

低复杂度分组预编码算法中,进行广义特征分解的矩阵束的维度降低,影响广义特征值及ρi,从而影响系统性能.
3.2 复杂度分析
算法的运算量主要集中于广义特征分解、格基约减和QR分解,因此本文重点考虑完成这3种运算需要的浮点运算次数.
假设对第i组用户数据预编码时,不发送该组用户数据的波束数为ri,则计算N个预处理矩阵需要的运算量为14
利用文献[14]中CLLL算法实现格基约减,则完成所有分组的格基约减运算需要的运算量为
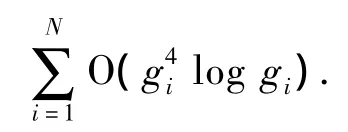
对n维方阵进行QR分解需要的浮点运算量为4n3/3,因此完成N次QR分解的运算复杂度为
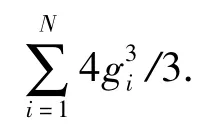
综上,本文提出算法的运算复杂度约为

与原分组预编码算法相比,本文算法复杂度的降低主要集中在计算Wi的过程中,计算复杂度由14NK3降低为.可见ri越大,本文算法减小的运算量越大.
4 仿真结果及分析
利用MATLAB建立多波束卫星系统前向链路仿真模型,以图1所示19个波束为一簇,用户位置随机产生,如图1中圆圈所示.表1给出了多波束卫星系统模型的参数.通过蒙特卡罗仿真分析本文算法在不同分组方案、不同ri条件下的运算复杂度及误码性能,并与文献[11]中的分组预编码算法进行比较.所有仿真均进行3 000次蒙特卡罗实验.文献[11]中分组预编码和本文算法分别用BLR-SSLNR-THP和LC-BLR-SSLNR-THP表示.本文不考虑用户分组优化问题,重点分析算法在下面两种简单但非常有效的分组方案下的性能.利用GS1和GS2分别表示第一种和第二种分组方案.不同分组方案及不同ri参数下的预编码算法用GSi-(r1,…,rN)表示.
第一种分组方案:将K个用户分为3组

第二种分组方案:将K个用户分为5组
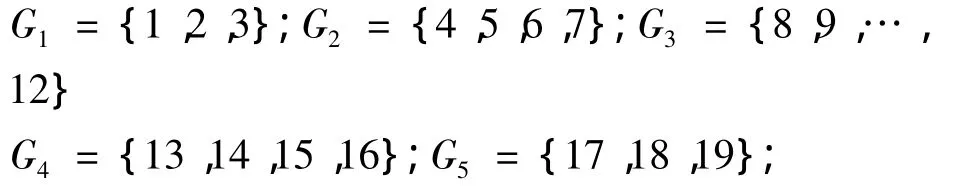

表1 多波束卫星系统模型参数
利用式(15),在3 000个信道衰落采样点下计算用户平均信干噪比.采用BLR-SSLNR-THP和LC-BLR-SSLNR-THP方案时的结果见图4.结果显示提出的低复杂度方案的性能损失很小,平均信干噪比在高信噪比时下降约0.4 dB.

图4 不同预编码方案用户平均信干噪比
表2、3给出不同分组方案、不同ri条件下,两种算法的浮点运算次数.结果显示ri越大,本文算法的复杂度越低,相比BLR-SSLNR-THP的复杂度降低越显著.另外,LRA-THP算法的复杂度约为1.34×106.可见,两种分组预编码算法的复杂度均远低于LRA-THP.图5为不同用户数情况下2种分组预编码算法的浮点运算次数,两种算法中均将用户分为3组,其中本文算法参数ri为(3,0,3).由图中结果可看出用户数越多,本文算法复杂度的降低也越明显.

表2 BLR-SSLNR-THP复杂度

表3 LC-BLR-SSLNR-THP复杂度
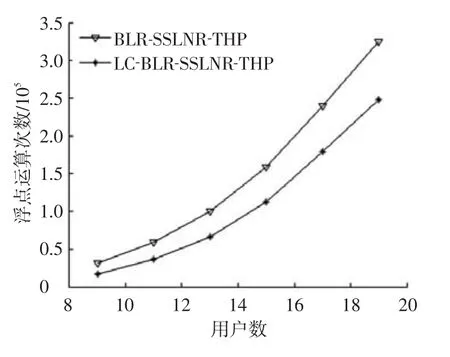
图5 不同用户数时预编码算法的运算复杂度
图6给出LC-BLR-SSLNR-THP在GS1-(7,0,7)条件下的误码性能,同时给出LRA-THP和BLR-SSLNR-THP的性能.与BLR-SSLNR-THP算法相比,本文算法的误码性能损失约0.4 dB.同时,由表2、3结果可看出,在该条件下本文算法的复杂度降低了约44.3%.

图6 不同预编码算法的误码性能
在第一种分组方案下对BLR-SSLNR-THP和LC-BLR-SSLNR-THP的误码性能进行仿真,结果见图7.图中给出本文算法在不同ri条件下的性能.结果显示,在 GS1-(3,0,3)条件下,本文算法的运算量降低了24%,同时性能损失 <0.1 dB;在 GS1-(7,2,7)条件下,算法的性能比BLR-SSLNR-THP差约1 dB,但降低的复杂度超过52%;可见,本文算法可以在几乎不损失性能的情况下,将运算复杂度降低24%.表4给出不同ri时,LC-BLR-SSLNR-THP的浮点运算次数和误比特率达到10-4时的信噪比.表中结果显示,通过调整参数ri,本文算法能够在误码性能和复杂度之间进行折中.

表4 LC-BLR-SSLNR-THP在不同ri条件下的性能比较
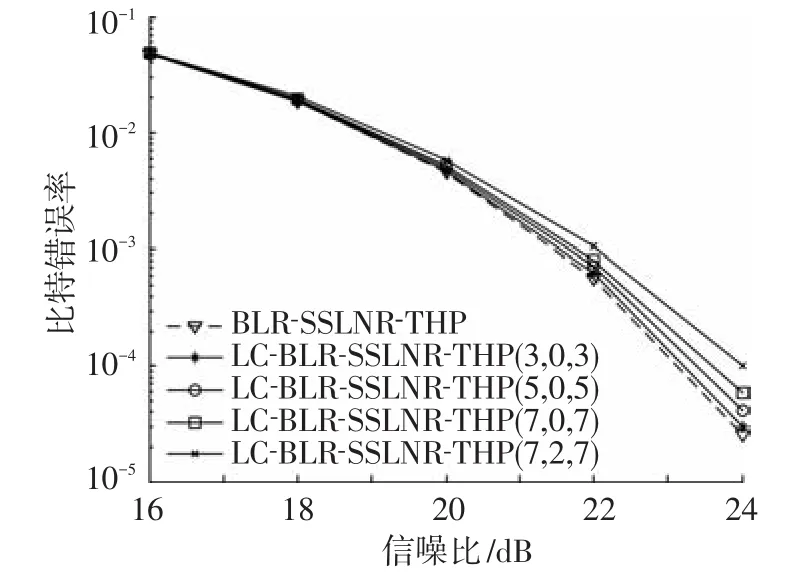
图7 第一种分组方案下分组预编码算法的性能
图8中的结果为本文算法在第二种分组方案下的误码性能曲线.对比不同ri条件下的算法性能,同样可看出ri越大,算法性能损失越大,同时复杂度降低也越多.在 GS2-(7,3,0,3,7)条件下,算法性能损失约为0.1 dB,此时复杂度降低了约45.3%.另外,与算法在第1种分组方案下的性能相比,在第二种分组方案下获得相同的误码性能需要更多的运算量,但算法的灵活性更高.

图8 第二种分组方案下分组预编码算法的性能
5 结语
本文在文献[11]基于SLNR的分组预编码算法基础上,提出一种适用于多波束卫星系统的低复杂度分组预编码算法.该算法充分利用多波束卫星信道特点降低运算复杂度.在不同分组方案、不同ri条件下分析算法的运算量及误码性能,结果显示,本文算法能够显著地降低LRA-THP的复杂度.而相比原分组预编码算法,本文算法能够将运算复杂度降低24%,同时使性能损失低于0.1 dB.改变本文算法中的参数ri,能够进一步降低算法复杂度,并在复杂度与误码性能之间取得灵活的折中.
[1]VIDAL O,VERELST G,LACAN J,et al.Next generation high throughput satellite system[C]//Proceedings of IEEE First AESS European Conference on Satellite Telecommunications.Rome:IEEE,2012:1-7.
[2]ARAPOGLOU P,LIOLIS K,BERTINELLI M,et al.MIMO over satellite:a review [J].IEEE Communications Surveys& Tutorials,2011,13(1):27-51.
[3]COTTATELLUCCI L,DEBBAH M,GALLINARO G,et al.Interference mitigation techniques for broadband satellite systems[C]//Proceedingsof 24th AIAA International Communications Satellite Systems Conference.San Diego:AIAA,2006:329-341.
[4]DI CECCA F,GALLINARO G,TIRRÒ E,et al.Onground beamforming and interference cancellation for next generation mobile systems[C]//Proceedings of AIAA International Communications Satellite System Conference.Ottawa:AIAA,2012.
[5]CHRISTOPOULOS D,CHATZINOTAS S,ZHENG G,et al.Linear and nonlinear techniques for multibeam joint processing in satellite communications [J].EURASIP Journal on Wireless Communications and Networking,2012,2012(1):1-13.
[6] ARNAU J,DEVILLERS B,MOSQUERA C,et al.Performance study of multiuser interference mitigation schemes for hybrid broadband multibeam satellite architectures [J]. EURASIP Journalon Wireless Communications and Networking,2012,2012(1):1-19.
[7]TRONC J,ANGELETTI P,SONG N,et al.Overview and comparison of on-ground and on-board beamforming techniques in mobile satellite service applications[J].International Journal of Satellite Communications and Networking,2014,32(4):291-308.
[8]DIAZ M A,COURVILLE N,MOSQUERA C,et al.Non-linear interference mitigation for broadband multimedia satellite systems[C]//Proceedings of International Workshop on Satellite and Space Communications.Salzburg:IEEE,2007:61-65.
[9]ZHENG Wei,LI Jianbo,LUO Yong,et al.Multi-user interference pre-cancellation for downlink signals of multi-beam satellite system [C]//Proceedings of InternationalConference on Consumer Electronics,Communications and Networks.Xianning:IEEE,2013:415-418.
[10]POGGIONI M,BERIOLI M,BANELLI P.BER performance of multibeam satellite systems with Tomlinson-Harashima precoding[C]//Proceedings of IEEE International Conference on Communications.Dresden:IEEE,2009:1-6.
[11]CHEN C,CHO T,CHUNG W.Block-lattice-reductionaided Tomlinson-Harashima precoder designs for MUMIMO downlink communications with clusters of correlated Users[J].IEEE Transactions on Vehicular Technology,2014,63(3):1146-1159.
[12]SADEK M,TARIGHAT A,SAYED A H.A leakagebased precoding scheme for downlink multi-user MIMO channels [J]. IEEE Transactions on Wireless Communications,2007,6(5):1711-1721.
[13]CHEN Rui,LI Jiandong,LI Changle,et al.Multi-user multi-stream vector perturbation precoding [J].Wireless Personal Communications,2013,69(1):335-355.
[14]GAN Y H,LING C,MOW W H.Complex lattice reduction algorithm forlow-complexity full-diversity MIMO detection [J].IEEE Transactions on Signal Processing,2009,57(7):2701-2710.
