S波段两状态LMS信道模型的自适应长期预测
2015-09-03赵旦峰
赵旦峰,廖 希,王 杨
(哈尔滨工程大学信息与通信工程学院,150001哈尔滨)
在静止轨道(geostationary,GEO)卫星通信系统中,陆地移动卫星传输时延约为266.6 ms,若信道状态最小持续时间大于传输时延,则回传到接收端的状态信息是有效的,能自适应[1-3]地调整发射端编码、调制等参数,进而减少深度衰落影响,降低系统平均误比特率,提高系统吞吐量[4].
目前,常用概率统计模型描述LMS信道衰落特性,建立LMS信道模型一般包含表征衰落变化深度的有限状态和快/慢变信号2个过程.目前,S波段常用的Loo模型[5]、两状态LMS信道模型[6-7]及其扩展模型[8]均能有效地描述阴影遮蔽对接收信号影响.
近年来,许多学者针对仅有几微秒时延的陆地移动衰落信道提出了不同的长期预测方法[9-11],而LMS信道的大时延特性增加了对未来衰落序列预测的难度.文献[12-13]分别提出低轨和GEO卫星通信系统的信道质量预测方法.文献[14]结合加权思想和最小均方误差(minimum mean square error,MMSE)算法预测未来长期内的信道状态和衰落序列,但仅适用于模型参数固定的三状态LMS信道模型[15],且固定的线性自回归(linear auto-regression,LAR)模型系数和错误传播恶化预测精度.
为解决上述问题,本文基于Markov链将S波段的阴影遮蔽建模为模型参数可变的窄带两状态Gilbert-Elliot信道模型,并利用迭代自适应长期预测(adaptive long-range prediction,ALRP)方法更新当前状态持续时间内LAR模型的系数,且利用最新观测值预测未来的衰落序列.最后分析算法复杂度和预测实时性,给出不同条件下预测的均方误差(mean square error,MSE),并与文献[14]中的长期预测(long-range prediction,LRP)比较.
1 Gilbert-Elliot信道模型
LMS通信系统的离散时间接收信号为

式中:xk为符号序列,ak为以符号速率采样的信道采样序列,sk为高斯白噪声.
在 LMS 传播信道中,采用 Gilbert-Elliot[16]窄带信道模型表征大尺度范围内阴影遮蔽状态的变化,并根据直射分量受到的衰落程度分为2个状态,即LoS条件到中度遮蔽范围为“好”状态,深度遮蔽到阻塞范围为“坏”状态,分别对应1、2.建立的信道模型见图1(a),包含状态生成器,传播参数生成器和衰落生成器.状态生成器利用离散的一阶Markov链控制状态之间的转移,由转移概率矩阵P=[pi|j]2×2描述,见图1(b)所示.其中,图1(b)中pi|j为初始时刻各状态之间的转移概率,bi为图1(a)在当前状态下输出的观测序列,其概率密度函数服从Loo分布[5].一旦进入新状态,就由式(2)的联合概率更新模型参数.
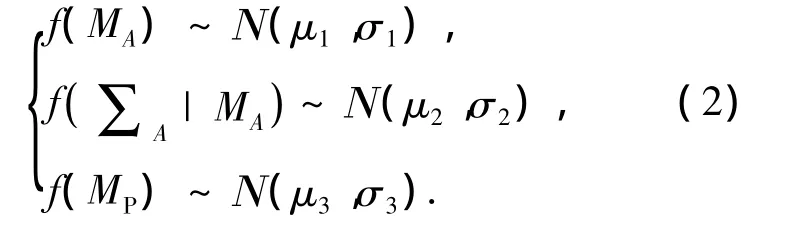
其中,
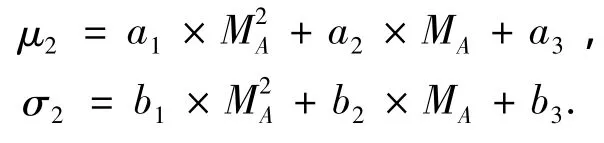
式中:MA,∑A分别为对数正态分布的均值和标准偏差,MP为平均多径功率,均以dB为单位.N(·)为高斯分布,系数ui,σi,ai,bi取决于环境类型、卫星仰角和方位角.如中级树阴影、卫星仰角60°、移动终端速度45 km/h,Gilbert-Elliot信道模型输出的接收信号衰落序列如图2所示.结果表明:此信道模型能准确地描述大范围内阴影遮蔽状态之间的转移及大尺度和小尺度衰落信号;且相比文献[14]的三状态信道模型,图1(b)所示的信道模型降低了状态转移的复杂度,且可变的传播参数增加了衰落的随机性.

图1 Gilbert-Elliot信道
2 LMS信道模型的ALRP方法
LMS信道中阴影遮蔽使接收信号在长期范围内波动(如S波段的最小状态持续距离约为3~5 m)导致各阶衰落序列之间存在相关性.利用各阶自相关系数和各阶转移概率,基于归一化加权思想[17]预测未来长期内信道状态.本文针对文献[1]存在的弊端提出一种适用于模型参数可变的两状态LMS信道模型的迭代自适应跟踪长期预测方法.
2.1 未来长期内信道状态预测
首先,以远小于符号速率的采样率fs得到序列A,并由样条插值使A与ak的速率匹配.设符号序列xk=1,由式(1)得到yk.然后,以频率fb从yk中抽样得到观测序列B=[bn,…,b1]T(长度为N).最后,以fc二次抽样得到状态观测序列C(长度为M),其k阶自相关系数定义为
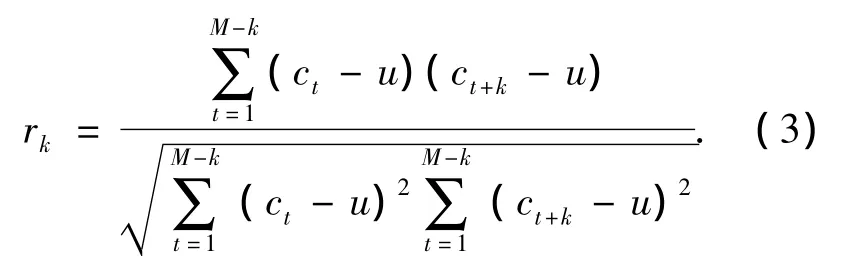
式中u为各阶状态观测序列的期望值.假设最大阶数为K,并将C中t时刻前的第K个状态作为初始状态,则各阶状态转移概率矩阵为
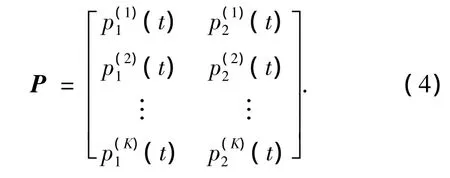
式(4)中各阶状态转移概率p(k)i(t)的归一化权重为
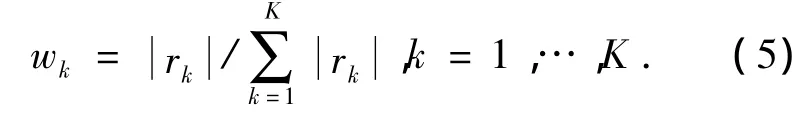
结合式(4)、(5),在t时刻预测出的状态概率分布为
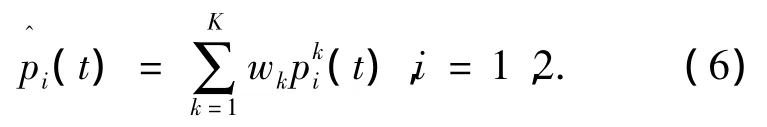
将最大概率max{p1,p2}作为t时刻预测出的信道状态,进而可预测出此状态持续时间内的衰落序列.
2.2 迭代自适应跟踪预测方法
假设采用一步预测,在预测出状态持续时间内,由MMSE算法计算t时刻LAR模型系数,并由迭代自适应跟踪方法更新各时刻系数,且将K个最新观测值作为LAR模型在各时刻的输入.具体过程如下.
首先,利用MMSE算法的正交化原则计算出t时刻信道状态i的优化系数为
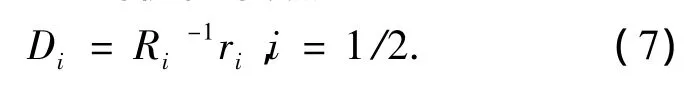
式中:Di=[di1,…,diK]T,Ri是观测序列的自相关矩阵,大小为K×K,其l行m列的元素为
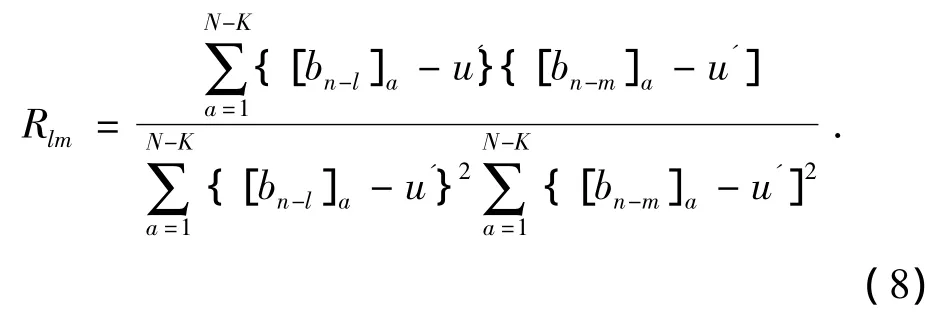
式中:bn-l/m=[bN-l/m,…,bK-l/m+1]T,u'为bn-l/m的期望值.
r为自相关向量,其系数为

式中:bn-k=[bN-k,…bK-k+1]T,,'分别为bn,bn-k的期望值.
然后,由式(10)预测出t时刻衰落值.
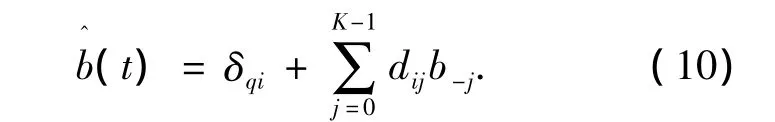
式中δqi为状态q到状态i的期望值偏差.
最后,更新LAR模型在各时刻系数为
式中:m为每一状态内预测的信道衰落数(与移动终端速度v和fb有关),Tb=1/fb为抽样间隔,μ为控制收敛速度的步长,e为前一时刻的预测误差,b为K个最新的观测值.
2.3 算法复杂度分析
假设各状态的观测序列长度为p,表1给出一个状态持续时间内ALRP方法在每一步所需要的乘法和加法次数.

表1 一个状态持续时间内的复杂度
2.4 实时性分析
在LMS通信系统中,卫星和地面站的相对运动会使直射分量和多径分量均受到多普勒频移的影响,其第n条路径的多普勒频移为
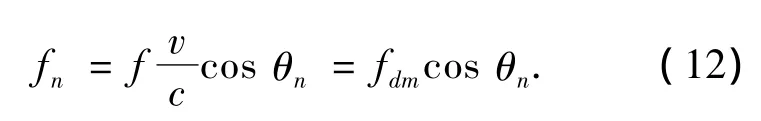
式中:f为载波频率,c为光速,θn为卫星仰角,fdm为最大多普勒频移.v越小,信道状态持续时间越长,状态转移次数越少,且信道衰落持续时间越长,提高对信道状态预测的准确性和自适应跟踪的精度;当状态持续时间Th≥266.6 ms时,接收端通过回传信道发送给发射端的信道信息具有实时性,能用于指导自适应传输.
3 仿真分析
仿真分析不同抽样频率fb和移动终端速度v下的预测性能及实时性和复杂度,且与文献[14]比较.采用均方误差(即未来长期内信道的预测值与实际值之差平方的统计平均)作为衡量标准.仿真参数为:S波段下行链路的频率2.2 GHz,符号速率为25 kb/s,采样序列A的长度为2×104(采样率fs=8×fdm),状态持续距离为5 m,慢衰落的相关距离为2 m,二次抽样频率fc=20 Hz,步长μ=0.01.同时,选择中级树阴影环境,卫星仰角60°作为仿真场景,初始状态转移概率为p2|1=0.172 4、p1|2=0.2.观测信道模型的传播系数如表2所示.信噪比(signal-tonoise,RSN)为0 dB,采用50个观测值的部分预测结果来说明ALRP方法的预测精度,如图3所示.

表2 两状态LMS信道模型模型参数
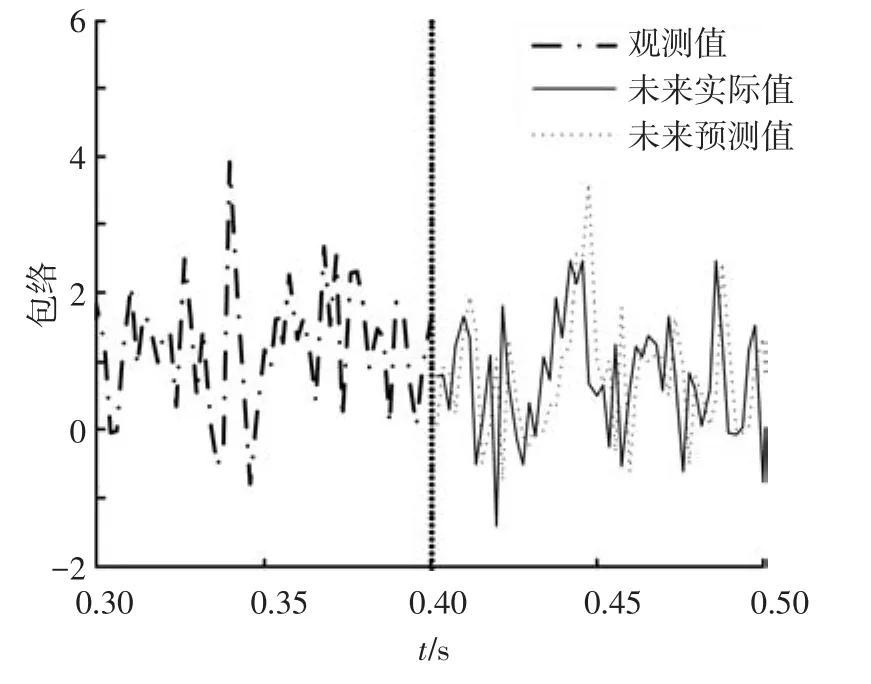
图3 ALRP预测结果(v=45 km/h,fb=500 Hz,K=10)
未来预测值和实际值很接近表明提出的预测方法能准确地预测出具有可变模型参数的两状态LMS信道模型在未来长期内的信道状态及衰落序列.
3.1 预测性能仿真分析
以fb≥2fdm从A中抽样得到观测序列B,fb越大抽样越精确.fb对ALRP性能的影响如图4所示.
结果表明:随着fb增加,ALRP和LRP的预测性能均改善,因为观测序列B的长度随fb的变大而增加,提高对未来长期内信道状态预测和AR模型系数更新的准确性.同时,在低RSN下,ALRP方法的最低抽样率仍好于LRP方法,而在中、高RSN下,ALRP方法的2fdm与LRP的5fdm接近.
随着v的增加fdm变大,相干时间Tc和信道状态持续时间Th均变小,增加了信道状态之间的转移、模型参数的更新次数和信号的衰落率,影响预测性能.假设fb=500 Hz,K=10,图5给出不同速度下MSE与RSN的关系曲线.
仿真结果表明:低RSN下,ALRP的预测误差一致,且均好于LRP在低速下的预测性能.高RSN时随着v变小MSE越小、预测性能改善程度越大;RSN=32 dB时,45 km/h比120 km/h改善约4×10-2;图5还表明,在45和60 km/h时,ALRP的预测性能比LRP改善约3×10-2,而在高速度下自适应跟踪的精度降低、ALRP方法的预测性能略差.
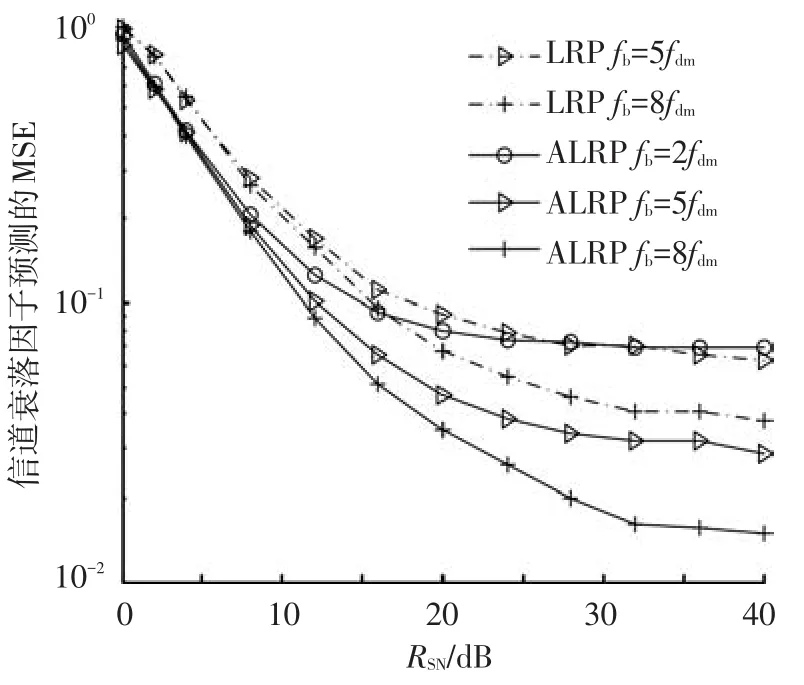
图4 抽样频率对MSE影响(v=45 km/h,K=10)
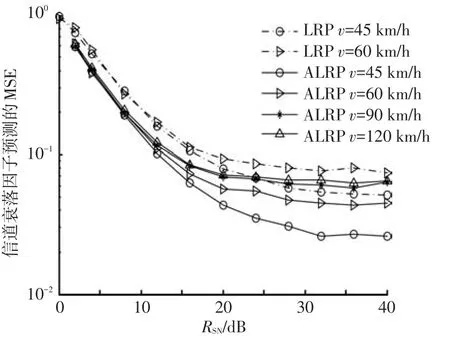
图5 移动终端速度对MSE的影响
图4、5均表明:随着RSN增加预测性能提高约2个数量级,并趋于收敛(即低噪声功率时的预测性能精确).
3.2 实时性和复杂度仿真分析
结合式(11)和表1、3给出S波段不同速度下的fdm、Tc、Th及未来一个状态持续时间内ALRP方法增加的复杂度.
结果表明:当v≤ 67 km/h时,Th≤266.6 ms,则预测出的信道状态和衰落序列可通过回传信道发送给发射端,具有实时性;相对比图5中预测性能的改善而言,由迭代自适应跟踪算法增加的复杂度是可接受的.
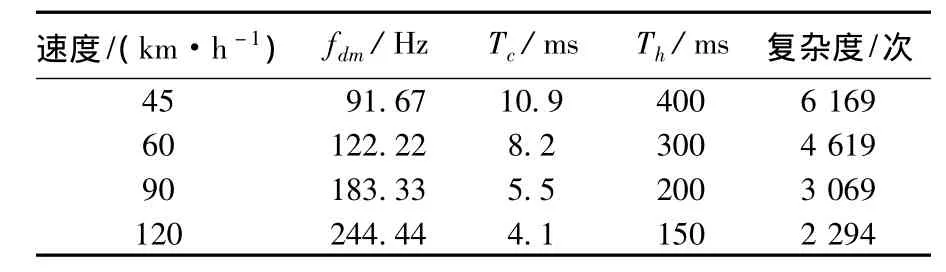
表3 不同速度下的实时性和增加的复杂度
4 结语
本文提出一种迭代自适应跟踪预测方法,相比文献[14],该信道模型在进入新状态时,需由联合分布更新模型参数;同时,预测出未来信道状态后,采用迭代自适应跟踪预测方法更新此状态持续时间内的LAR模型系数,并利用观测序列中K个最新的观测值预测未来信道的衰落序列,解决系数不变和错误传播问题.仿真结果表明:该方法能精确预测出模型参数可变的两状态LMS信道模型在未来长期内的信道状态和衰落序列.相比LRP方法,改善预测性能,且具有实时性和低复杂度优点,可进一步扩展到S波段多场景下的单卫星或双卫星窄带LMS信道模型的长期预测中.
[1] HALLEN A D,HU Shengquan,HALLEN H.Longrange prediction of fading signals[J].IEEE Signal Processing Magazine,2000,17(3):62-75.
[2] HALLEN A D.Fading channel prediction for mobile radio adaptive transmission systems[J].Proceedings of the IEEE,2007,95(12):2299-2313.
[3]TAO Jia,HALLEN A D,HALLEN H.Data-aided noise reduction for long-range fading prediction in adaptive modulation systems [J]. IEEE Transactions on Vehicular Technology,2013,62(5):2358-2362.
[4] GOLDSMITH A J, GHEE C S. Adaptive coded modulation for fading channels[J].IEEE Transactions on Communications,1998,46(5):595-602.
[5]LOO C.Statistical model for a land mobile satellite link[J].IEEE Transactions on Vehicular Technology,1985,34(3):122-127.
[6]CERDEIRA R P,FONTAN F P,BURZIGOTTI P,et al.Versatile two-state land mobile satellite channel model with firstapplication to DVB-SH analysis [J].International Journal of Satellite Communications and Networking,2010,28(5-6):291-315.
[7] HEYN T,EBERLEIN E,ARNDT D,et al.Mobile satellite channel with angle diversity:the MiLADY project[C]//ProceedingsoftheFourth European Conference on Antennas and Propagation(EuCAP).Barcelona:IEEE,2010:1-5.
[8]ARNDT D,HEYN T,KONIG J,et al.Extended twostate narrowband LMS propagation model for S-band[C]//Proceedings of the International Symposium on Broadband Multimedia Systems and Broadcasting(BMSB).Seoul:IEEE,2012:1-6.
[9]HEIDARI A,MCAVOY D,KHANDANI A K.Adaptive long-range prediction ofmobile fading[C]//23rd BiennialSymposium on Communications. Kigston,Ont.:IEEE,2006:219-222.
[10]HEIDARI A,KHANDANI A K,MCAVOY D.Adaptive modelling and long-range prediction of mobile fading channels[J].IET Communications,2010,4(1):39-50.
[11]SCHMIDT J F,COUSSEAU J E,WICHMAN R,et al.Low-complexity channel prediction using approximated recursive DCT [J].IEEE Transactions on Circuits and Systems I:Regular Papers,2011,58(10):2520-2530.
[12]ZHENG Yadan,DONG Mingke,ZHENG Wei,et al.Prediction method for channel quality indicator in LEO mobile satellite communications[C]//15th International Conference on Advanced Communication Technology(ICACT).Pyeong Chang:IEEE,2013:799-803.
[13]ZHENG Yadan,DONG Mingke,JIN Ye,et al.CQI prediction for shadow fading in LTE-compatible GEO mobile satellite communications system[J].Advanced Materials Research,2013,756:2137-2141.
[14]周坡,曹志刚.基于马尔科夫过程的卫星移动信道模型及长期预测方法[J].电子与信息学报,2011,33(12):2948-2953.
[15]FONTAN F P,CASTRO M V,CABADO C E,et al.Statistical modelingoftheLMS channel [J].IEEE Transactions on Vehicular Technology,2001,50(6):1549-1567.
[16]周洁,焦健,杨志华,等.深空通信中Ka频段自适应纠删编码研究[J].宇航学报,2013,34(1):92-98.
[17]刘震,王厚军,龙兵,等.一种基于加权隐马尔科夫的自回归状态预测模型[J].电子学报,2009,37(10):2113-2118.
[18]LACOSTE F,VILLACIEROS B M,CERDEIRA R P,et al.SISO and MIMO enhanced 2-state modelling of the land mobile satellite channel for various frequencies,environments and elevation angles[C]//8th European Conference on Antennas and Propagation(EuCAP).The Hague:IEEE,2014:2277-2281.
