无阀压电微泵用平面锥管内部流动附壁效应

何秀华，朱学斌，杨 嵩，邓志丹

(1.江苏大学 能源与动力工程学院，212013江苏 镇江;2.江苏大学 流体中心，212013江苏 镇江;3.江苏大学 理学院，212013江苏 镇江)

微流管作为无阀压电泵中的关键组成部分，其流阻特性很大程度上决定压电泵的性能［1-2］.已开发的无阀压电泵用特殊流管结构包括锥形管［3］(扩散/收缩管)、TESLA 管［4］、涡旋管［5］、“Y”型管［6］、三通管［7-8］等.锥形管(扩散/收缩管)结构简单，易于加工，对其性能和结构进行优化是提高无阀压电泵性能的重要途径，目前，无阀压电泵中应用最为广泛的流管为平面锥管.锥管扩散方向的内部流动状态随着锥管角度的变化而变化，当角度很小时，锥管内流动没有分离现象，流速分布关于锥管中心线对称;随着锥管角度的增大，流动发生分离，由于附壁效应(康达效应)，只在锥管的一侧壁面发生分离，而另一侧没有分离，形成附壁射流;当锥管角度很大时，锥管两侧都会出现稳定的漩涡.锥管内是否发生附壁射流现象与锥管角度、雷诺数和进口形状相关［9］.Byron 等［10］用PIV研究了高深宽比锥管内部流动附壁现象.Tsui［11］等研究了平面锥管内部流动，Wang［12］等在100＜Re＜2 000情况下研究了平面锥管内部流阻随雷诺数变化情况.Vishali等［13］探究了低雷诺数下锥管流阻系数比随锥角变化情况.Ha等［14］研究了背压和流量随振动频率变化情况，这些研究都采用一半锥管结构并应用对称边界条件进行模拟，没有考虑锥管内流动存在的附壁流动现象.

本文采用文献［1，15］中经过试验验证的CFD数值模拟方法，对不同角度锥管内附壁流动进行研究，分析附壁效应对锥管流阻系数的影响.

1 无阀微泵用锥管结构及流动分析

1.1 无阀微泵工作原理

无阀微泵工作原理如图1所示.一个周期内随着振动薄膜的位移，流体从两侧锥管被吸入和排出泵腔，由于锥管扩散、收缩两个方向流阻不同，两个锥管的流量产生差异，从而实现流体在无阀微泵中的单向输送.

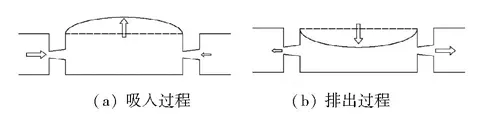
图1 无阀压电泵的工作原理图

1.2 锥管结构

本文研究的平面锥管结构如图2所示，包括锥管及两个缓冲腔，其中锥管和缓冲腔关于锥管的中心线是对称布置的.进口缓冲腔与出口缓冲腔结构相同，长度为4 mm，宽度为6 mm，锥管最小截面宽度d和高度h均为0.15 mm，锥管长度L为最小截面宽度d的10倍，进口圆角半径r为0.15 mm，本文研究的平面锥管角度θ为5～40°.

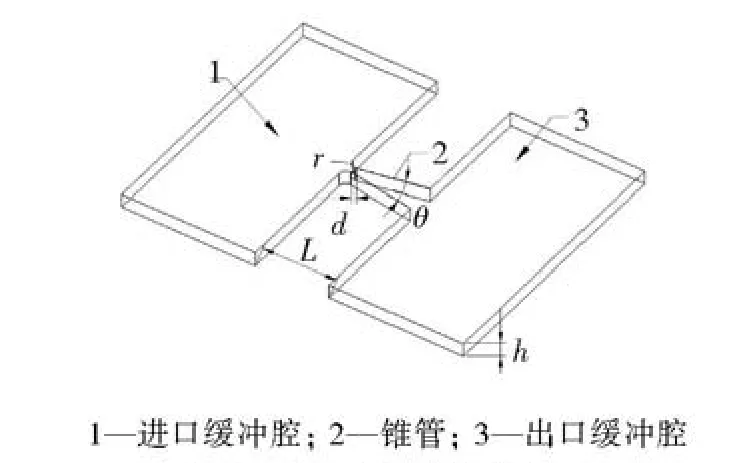
图2 平面锥管结构示意

1.3 扩散/收缩管流动损失及效率分析

锥管流阻系数可以根据流体流经扩散/收缩管的压力损失进行计算.

扩散方向流阻系数为

收缩方向流阻系数为

式中:Δpd、Δpn分别为沿扩散方向和收缩方向上的流动压力损失，Pa;ρ为流体密度，kg/m3;vd、vn分别为扩散方向和收缩方向在流管最小截面处的平均速度，m/s.

定义收缩方向与扩散方向流阻系数的比值为流阻系数比λ，即

对于锥管无阀压电泵，其流阻系数比越大，则泵送流量就越大，无阀压电泵的效率越高.

2 数值模拟

2.1 边界条件设置及流动模型选择

白亚磊等［16］用k-ε湍流模型模拟二维锥管内部附壁效应.Tesar等［17］采用 RNG湍流模型模拟了合成射流激励器内平面锥管中的附壁效应.本文利用CFX软件对锥角为5～40°的平面锥管内部流动进行模拟，采用k-ωSST湍流模型［1，16］，该模型对边界层内流动分离的预测较为准确.

流动介质为不可压缩的水，密度为1 000 kg/m3，动力黏度系数μ为0.001(N·s)/m3，忽略流体重力的影响，设进口边界条件为速度进口边界条件，出口设相对压力为零，设定时间为10 s，时间步长为 0.001 s.根据Re=ude/υ(其中de为特征宽度，u为最小截面处速度，υ为运动黏度)该计算模型中雷诺数为300～3 000，由层流向湍流过渡的经验公式［17］Ret=30L/Dh，得到该数值模拟的过渡雷诺数为300.

2.2 网格划分

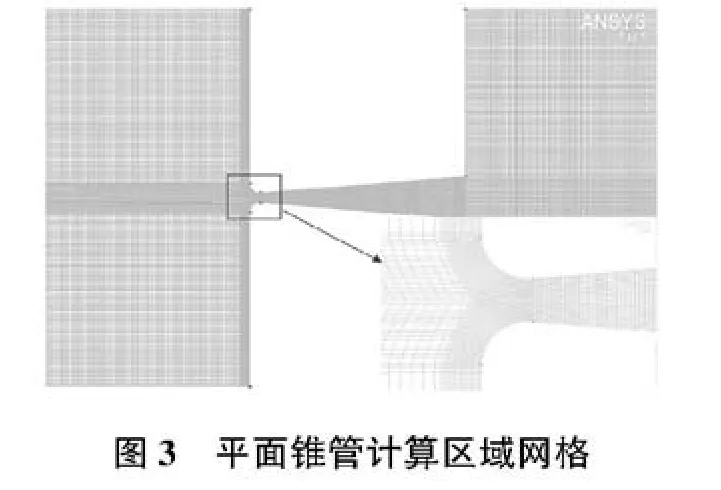
扩散/收缩管计算区域网格划分如图3，锥管模型采用结构化网格进行划分，该计算区域网格关于锥管中心线对称分布，由于锥管与进(出)口缓冲腔衔接位置处压力梯度较大，因此该处网格进行加密.

2.3 网格无关性验证

对锥管角度为10°的平面锥管进行网格无关性验证，分别对60万、120万、200万和260万4种网格数目的模型进行计算，其扩散流阻系数如图4所示.200万和260万网格模型模拟结果基本一致，120万和200万网格模型模拟的扩散流阻系数最大相对误差不足3%.

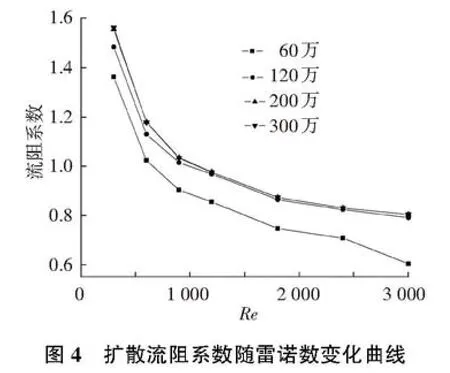
最大雷诺数Re=1 200时，对角度θ为10°的平面锥管的压力进行研究，计算结果如图5所示.随着网格数量的增加，发现有3处明显变化(在图中分别标记为1、2、3)，最小截面处(标记1)网格数为60万，模型模拟结果中压力分布更加尖锐，明显不同于其他两种网格数模拟结果;锥管内部(标记2)，网格数为60万的模拟结果中，压力梯度变化比其他两种网格数的模拟结果更加接近锥管进口;120万和200万网格模型的模拟结果压力云图基本相同，压力最大值相差不到1%，而60万网格模拟的结果比其他两种网格数的模拟结果压力小10%.为了提高计算效率，综上所述本研究采用120万网格模型进行数值模拟.

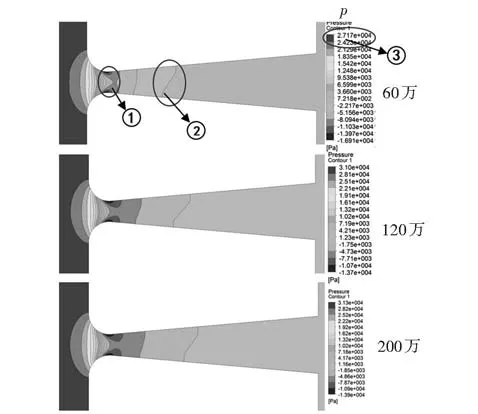
图5 Re=1 200时3种网格锥管内压力分布云图

3 结果与分析

图 6 为Re=900 时，θ=5°，20°和35°的平面锥管内流体流动分布图.由图6可知，锥管内部流体流动主要分 3种状态:1)稳定状态，如图6(a)θ=5°所示，由于角度较小，流体与两侧壁面无边界层分离.2)附壁状态，如图6(b)θ=20°所示，主射流贴附在一侧壁面，另一侧出现漩涡.由于平面锥管内部射流发生微弱扰动，使两侧的压力损失不均衡，主射流会相应的产生微弱的倾斜，导致流体偏转，倾斜的一侧空间较另一侧小，压力恢复较另一侧慢，于是就形成了主射流两侧的压力不均衡，最终诱导主射流附壁.3)射流状态，如图6(c)θ=35°所示，射流从两侧壁面脱离(全分离扩散管)，且射流两侧都出现明显漩涡.

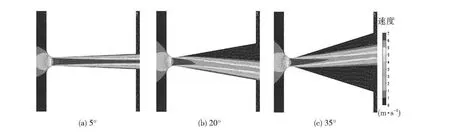
图6 Re=900时θ=5°、20°和35°锥管内流体流动分布图

表1为θ在5～40°、Re在300～3 000的锥管内流动附壁情况.可以看出:在角度为5°，雷诺数在300～3 000时，平面锥管内流动为稳定状态.在Re=300，θ范围为5～40°时，锥管内流动都为稳定状态.当θ在10～30°范围内，Re＞ 600时，锥管内部都会发生附壁现象.当θ=35°时，Re=600和900时，流动呈射流状态;当Re＞900时，锥管内流动发生附壁现象.θ=40°时，Re=600～1 200，平面锥管内部流体流动呈射流状态;当Re＞1 200时，锥管内流动发生附壁现象.

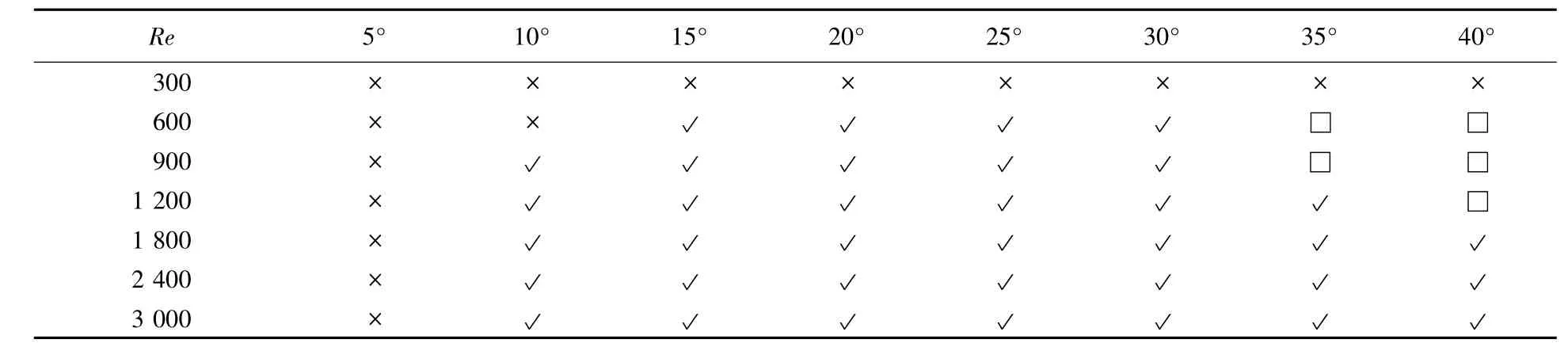
表1 θ在5～40°、Re为300～3 000下的流动状态

3.1 内部流场分析

图7为θ=10°平面锥管内Re=2 400时，流体轴向速度分度图.锥管内部均匀分布取5个垂直端面，如图(a)所示.速度云图关于中部平面对称分布，平面锥管内部流体流动出现明显的附壁现象，流体向一侧壁面偏转并且附壁，且另一侧出现回流现象.由于腔体高度h较低，锥管中出现二次流，从第二个平面上可以看出在有流动分离的一侧壁面产生对称分布的漩涡.图(b)为锥管中部平面速度分布图，锥管入口处速度呈凹形分布，越靠近扩散管出口端轴向速度越小，同时最大轴向速度区域也越来越小.

为了观测锥管中心和射流中心的流体展向速度，设监测方案如图8所示，监测面为锥管中部平面，锥管进口中心设为坐标原点，沿锥管中心线方向设为X轴，沿锥管展向方向设为Y轴;线段A表示射流中心线，线段B表示锥管中心线.

图7 θ=10°，Re=2 400的平面锥管内轴向速度分度图

图8 监测示意图

图9为Re=1 800时，θ为10～40°的平面锥管内部展向速度(Y轴方向)分布图.如图10(a)所示，由于θ=10°平面锥管出口宽度较小，射流中心线上展向速度与锥管中心线上展向速度相差较小，且两条监测线上的流体展向速度都在X=0.001 1处达到最大值，锥管中心线上的展向速度降低比较迅速.如图10(b～g)所示，随着X的增加，射流中心线上展向速度增大且逐渐趋于稳定;锥管中心线上展向速度在锥管进口处增加速率与射流中心线上展向速度增率一致，达到最大值后随着X的增加迅速降低.扩散角越大展向速度越大;扩散角越大，锥管中心线上最大展向速度点越接近锥管进口;扩散角越大，两条检测线上最大展向速度差值越来越大.

图10为θ=10°时，3/4L处不同雷诺数下，轴向速度分布曲线图.可见在Re=600时，锥管内流动处于稳定状态，其速度分布关于平面锥管中心线对称分布;Re＞600时，其速度分布明显向一侧偏转，流动处于附壁状态，且雷诺数越大，射流越贴近壁面，另一侧出现负速度.

3.2 流阻系数分析

图11为Re在300～1 200扩散流阻系数随扩散角度的变化曲线图，根据表1所示，θ在5～40°，Re=300时，锥管内部流体流动处于稳定状态，其扩散流阻系数随扩散角增大逐渐减小，且随着扩散角增大，扩散流阻系数变化趋于平缓.当Re在600～1 200时，流体流动处于稳定状态时，扩散流阻系数随锥角增大逐渐减小;流动处于附壁状态时，扩散流阻系数随锥角增大缓慢增加;当流动处于射流状态时，扩散流阻系数相对附壁状态明显增加，并且随着角度变化不大.

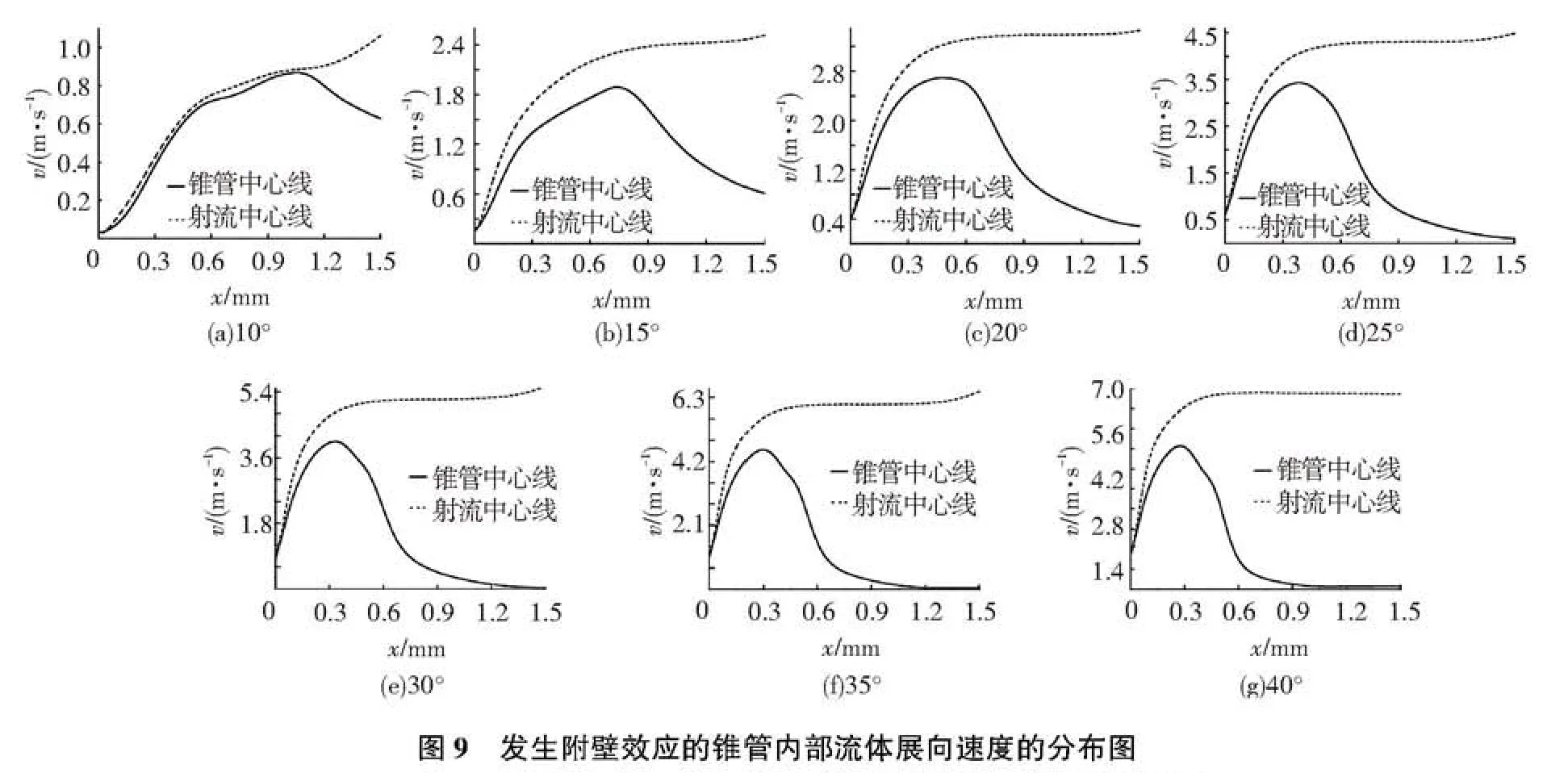
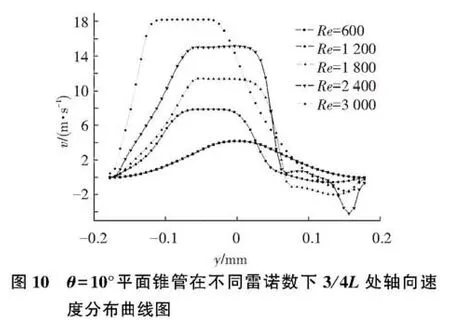
图12为Re在1 800～3 000流阻系数随扩散角的变化曲线图，稳定状态下扩散流阻系数迅速降低，θ=10°时流阻系数达到最小值;在附壁状态下，扩散流阻系数随着锥管扩散角的增大而增大，当θ≥30°时开始减小.同一角度其流阻系数随着雷诺数的增大逐渐降低.

图13为Re在300～3 000时收缩流阻系数随角度变化曲线图.同一雷诺数下随着收缩角度的增大，收缩流阻系数逐渐减小，并且随着角度的增大其变化趋势平缓;同一角度，随着雷诺数的升

3.3 流阻系数比分析

图14为Re在300～3 000下流阻系数比随角度变化曲线图，可见在模拟范围内，θ=10°时其流阻系数比最大，当Re=3 000时，其流阻系数比最大为1.67.当θ≤10°时，流阻系数比随着雷诺数的增大而增大;当θ≥10°时，流阻系数比随着雷诺数的增大而逐渐降低.当θ＜15°时，相同角度下雷诺数越大流阻系数比越大;当15°≤θ＜30°时，相同角度下雷诺数越大流阻系数比越小;θ=35°时，Re在 600～3 000，其流阻系数比基本相同.Re=300，其流阻系数比随着角度的增大变化不大.流阻系数比在稳定状态和射流状态下随角度增大变化不大，而在附壁状态下随着角度增大迅速降低.

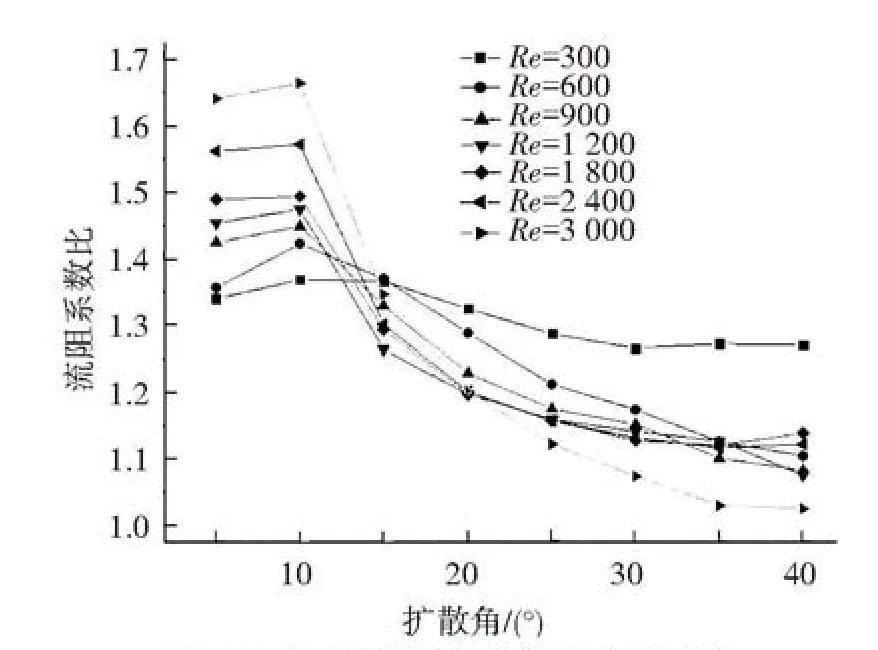
图14 流阻系数比随角度变化曲线

4 结论

1)Re在 300～3 000，锥管角度在 5～40°时，扩散方向流动可以分为3种状态，即稳定状态、附壁状态和射流状态.锥管角度在10～35°时，锥管内流动易于发生附壁效应，且随着雷诺数的增加，射流越来越贴近壁面.

2)模拟范围内，流阻系数随着雷诺数增大而减小.Re在300～1 200，平面锥管内流动处于稳定状态时，扩散流阻系数随着扩散角的增大明显降低;流动处于附壁状态时，扩散流阻系数随着扩散角的增大缓慢增加;射流流动时，扩散流阻系数相对附壁状态时明显升高，且随着扩散角增大而缓慢降低.Re在1 800～3 000，附壁状态下扩散流阻系数在扩散角为30°时达到最大值.

3)Re=300时，流阻系数比随着角度的增大变化不大.模拟范围内，流阻系数比在稳定状态和射流状态下基本保持不变;在附壁状态下，流阻系数比随着角度增大迅速降低.

［1］何秀华，禚洪彩.无阀压电泵用平面锥管内部流动特性［J］.排灌机械，2012，30(5):532-537.

［2］ SINGHAL V，GARIMELLA S V，RAMAN A，et al.Microscale pumping technologies for microchannel cooling system［J］.Applied Mechanics Reviews，2004，57(3):191-221.

［3］ARVIND H，MUTHUKUMARAN P.Geometrical tuning of microdiffuser/nozzle for valveless micropumps［J］.Journal of Micromechanics and Microengineering，2011，21(4):35-45.

［4］何秀华，邓许连.压电无阀微混合器的数值模拟［J］.排灌机械工程学报，2011，29(4):292-296.

［5］ IZZO I，ACCOTO D.Modeling and experimental validation of a piezoelectric micropump with novel nomoving-part valves［J］.Sensors and Actuators A:Physical，2007，133(1):128-140.

［6］张建辉，黎毅力.“Y”型流管无阀压电泵流量及流管流阻特性分析［J］.机械工程学报，2007，43(11):136-141.

［7］邓志丹，李富.并联三通全扩散/收缩管无阀压电泵的性能［J］.排灌机械工程学报，2013，31(1):20-24.

［8］何秀华，蔡盛川.一种三通结构的双腔无阀压电泵:中国，CN201310555240.3［P］.2014-3-19.

［9］华绍曾，杨学宁.实用流体阻力手册［M］.北京:国防工业出版社，1985:178-246.

［10］BYRON D E，MICHAEL W P.An investigation of bimodal jet trajectory in flow through scaled models of the human vocal tract［J］.Experiments in Fluids，2006，40:683-696.

［11］TSUI Y Y，LU S L.Evaluation of the performance of a valvelessmicropump by CFD and lumped-system analyses［J］.Sensors and Actuators A:Physical，2008，148:139-148.

［12］WANG Y C，HSU J C，KUO P C，et al.Loss characteristics and flow rectification property of diffuser valves for micropump applications［J］.International Journal of Heat and Mass Transfer，2009，52:328-336.

［13］VISHALl S， SURESH V， GARIMELLA J.Low Reynolds number flow through nozzle-diffuser elements in valveless micropumps［J］.Sensors and Actuator A，2004，113(2):94-103.

［14］HA D H，PHAN V P，GOO N S，et al.Threedimensional electro-fluid-structural interaction simulation for pumping performance evaluation ofa valveless micropump［J］.Smart Materials and Structures，2009，18(10):104015.

［15］YUAN Shouqi，YANG Song.Design and experimental study of a novel three-way diffuser/nozzle element employed in valveless piezoelectric micropumps［J］.The Brazilian Society of Mechanical Sciences and Engineering，2014.DOI:10.1007/s40430-014-0176-5.

［16］白亚磊.康达效应在流量测量中的研究与应用［D］.南京:南京航空航天大学，2007.

［17］TESAR V，HUNG C H.ZIMMERMAN W B.Nomoving-part hybrid-synthetic jet actuator［J］.Sensors and Actuators A:Physical，2006，125(2):159-169.