GA优化的RBF神经网络外骨骼灵敏度放大控制

龙 亿，杜志江，王伟东

(机器人技术与系统国家重点实验室(哈尔滨工业大学)，150001哈尔滨)

穿戴式外骨骼机器人，与人体高度贴合，可增强人体的力量与耐力，缓解人体疲劳.BLEEX下肢外骨骼机器人是由美国加利福利亚Berkeley分校研制的，于2004年进行了样机试验.BLEEX采用液压驱动系统，所有传感器安装在外骨骼机器人上，包括力/力矩传感器、位置码盘等，所提出的控制方法称为灵敏度放大控制(sensitivity amplification control，SAC)［1-2］.在SAC 中，灵敏度被定义为外骨骼的输出运动信息与人机交互信息之间的关系，所以如果控制灵敏度在合适范围内，就可以减小人机交互作用，使外骨骼实现高度跟随人体运动轨迹.SAC方法是基于模型的控制，其控制效果取决于系统动态模型的精确程度，而外骨骼机器人是多自由度的非线性系统，要建立其精确的数学模型非常困难［3］.神经网络在机器人系统的动力学辨识方面得到了广泛的应用［4-5］.如下肢外骨骼的动力学精确模型的建立，一是离线的BP网络训练;二是系统的模式识别.运用BP网络来学习外骨骼的逆模型，网络的输入层为外骨骼关节的运动参数(角度、角速度、角加速度)，输出为力矩，采用正模型来获取实验数据，离线学习得到BP网络［6］.然而，BP网络每一次学习都需要重新调整权值，收敛速度慢，离线学习得到的BP网络的泛化能力难以得到保证.基于外骨骼单腿的三连杆模型，使用最小二乘法，运用实验手段对外骨骼模型中的参数(如刚度力矩、摩擦力等)进行了辨识［7］，但是全部过程需要大量的实验数据，耗时长.

针对外骨骼机器人系统有效地在线学习方法报道很少，本文设计了一种基于遗传算子(GA)优化的径向基函数(RBF)网络在线学习方法，获取外骨骼机器人的动力学模型，并将模型用于SAC中.

1 灵敏度放大控制原理

1.1 灵敏度放大控制的定义

灵敏度放大控制(SAC)是美国Berkley外骨骼系统(BLEEX)采用的控制方法，其控制原理如图1.其中，Ghm是人机交互模型，Gexo是外骨骼的动力学模型，Td是外部干扰力矩，包括人施加的人机作用力以及环境的干扰力，Ta是外骨骼驱动器施加的力矩，q=［q，，］为外骨骼的输出轨迹参数.

由图1可得

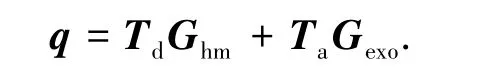
定义系统的灵敏度为

S表示外骨骼的输出轨迹对外在力的感应程度，S越大，表示Td对q的影响越大.

考虑人机交互力矩以及机构的阻尼、摩擦等，将图1改写为闭环的形式，如图2所示，其中，Thm是人机交互力矩，Ta是驱动器施加的力矩，α是放大系数，G'exo是外骨骼的逆动力学模型，qhm人体运动轨迹，即是外骨骼的目标运动轨迹.一般地，Ta=(1-α-1)G'exo，那么可以推导出新的灵敏度为

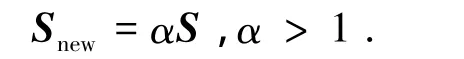
图1 SAC原理

图2 SAC闭环控制

1.2 SAC控制律

外骨骼实体机构如图3所示，每一条腿有两个主动自由度，踝关节不加驱动，驱动部分由液压缸完成.不失一般性，外骨骼机器人的动力学方程可以表示为

其中:M(q)∈R2×2是惯性项，C(q，)∈R2×2是阻尼与摩擦项，G(q)∈R2×1是重力项，T∈R2×1是关节力矩，D∈R2×1为未建模动力学以及干扰项.

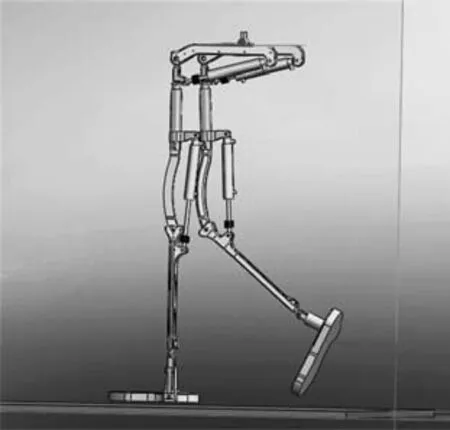
图3 外骨骼机器人模型

在SAC中，设计控制律为［8］

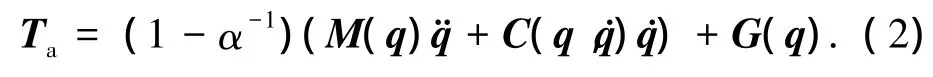
在式(1)中，T=Ta+Thm，可得

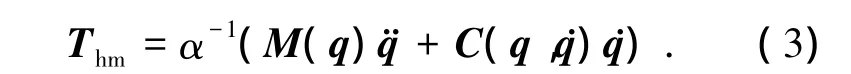
式(3)表明，α越大，Thm越小，即是灵敏度增大了，人机交互力矩就会减小，外骨骼的跟随性就会越好.

2 GA优化RBF

RBF的性能很大程度上取决于中心矢量、基宽度参数以及权值，用GA优化RBF结构能够获得较好的性能［9-11］.本文权值由设定的算法进行在线更新，在已知输入值范围的条件下，用GA优化出RBF网络最佳的中心矢量与基宽度.

GA优化RBF网络流程见图4.

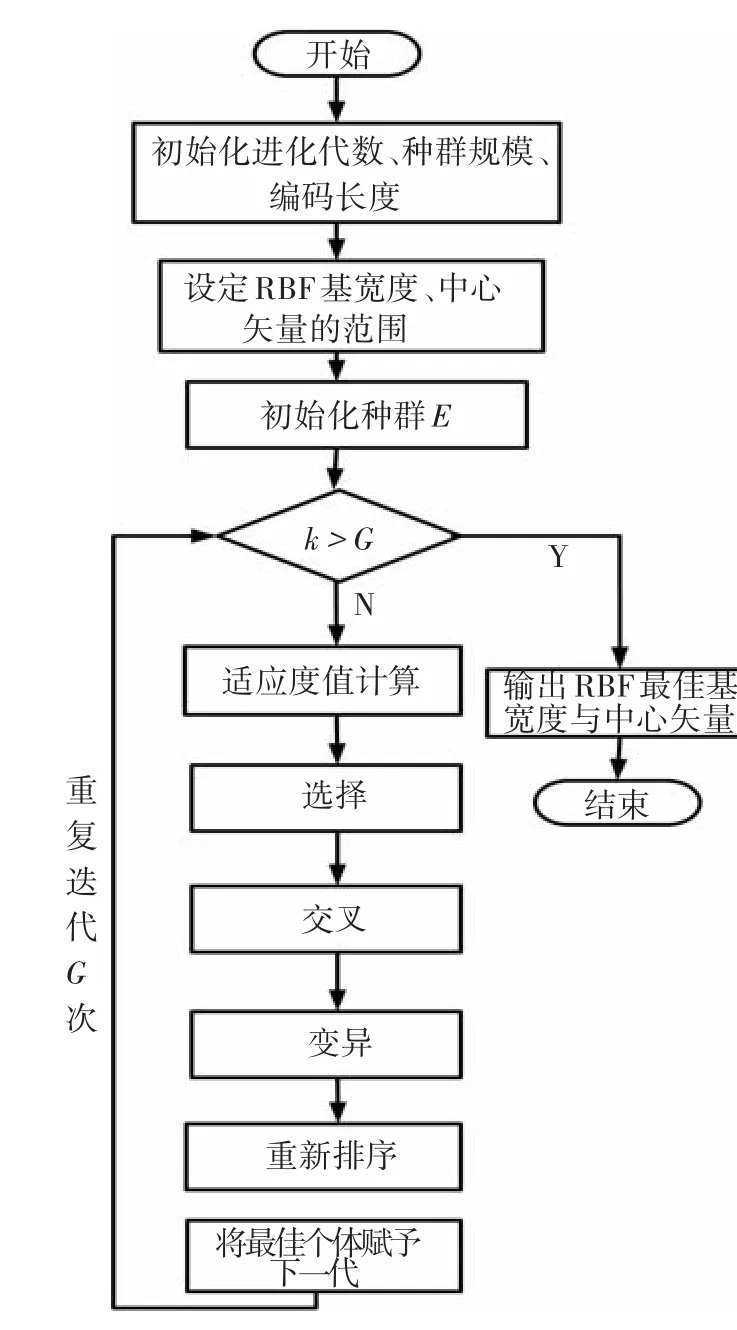
图4 GA优化RBF网络的基本流程

设定进化代为G=250，种群规模为30，编码长度为10.要设计的RBF网络是用来学习外骨骼动力学方程中的矩阵M(q)、C(q，)以及G(q)，分别通过GA获得相应的中心矢量

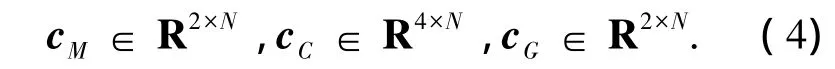
式中:cM、cC、cG为中心矢量，N为隐含层节点数.基宽度可以由下面的经验式获得:

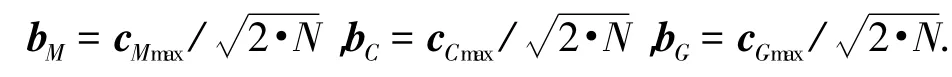
式中:bM、bC、bG为基宽度，cMmax，cCmax，cGmax为中心矢量元素的最大间隔.进行GA优化，得到优化后的 RBF网络的基宽度与中心矢量.对学习M(q)的RBF网络，GA优化RBF网络的结果如图5，迭代到20代左右即可获得最佳个体.

图5 GA优化中心矢量与基宽度的收敛过程

3 RBF在线学习外骨骼动力学模型

外骨骼机器人系统由于其高度的非线性以及外部环境的影响，很难求得精确的动力学模型，借助神经网络的学习能力，构造一种在线学习的RBF网络，可获取更为准确的动力学方程.本文提出了RBF网络在线学习外骨骼动力学模型(1)中的矩阵M(q)、C(q，)以及G(q).在RBF的结构中，输入向量为X=［x1，x2，…，xn］，映射到隐含层采用高斯径向基函数

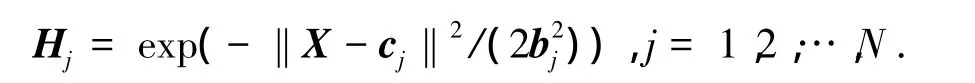
式中:N为隐含层节点数，Hj为jth节点隐含层的输出，bj为jth节点的基宽度，cj为jth节点中心矢量.

外骨骼的动力学模型中，矩阵M(q)、C(q，)以及G(q)是关于关节角度、角速度的矩阵.对于M(q)、C(q，)以及G(q)，基于(4)中的中心矢量与基宽度，输入矢量分别为关节角度与角速度的组合，通过高斯径向基函数，可以得到隐含层的输出为

其中，输入矢量分别为

式中:bM(j)、bC(j)、bG(j)分别为jth节点的基宽度，cM(j)、cC(j)、cG(j)分别为jth节点的中心矢量，t是时间变量，学习过程如图6，输入是关节的角度(角速度)，经过隐含层的映射，然后与当前时刻的权值相乘，加和后即可得矩阵(q)(q，)，(q))输出的元素，每个时刻对权值进行在线更新.

设外骨骼跟随人体轨迹的角度、角速度、角加速度误差为

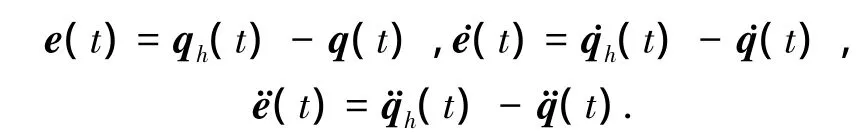
式中:qh(t)是人体轨迹，q(t)是外骨骼轨迹，定义s(t)(t)+λe(t)，其中，λ是正常数，定义等效速度与等效加速度为

式中:κ是正常数.权值的更新是根据实际的轨迹误差以及误差变化率构造的，权值更新的表达式如下［12-13］:

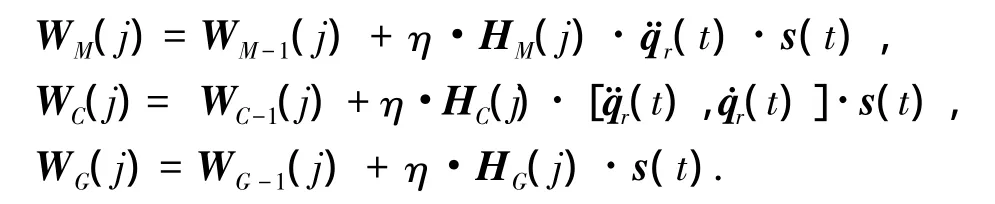
式中:WM-1(j)、WC-1(j)、WG-1(j)为初始权值矩阵，WM(j)、WC(j)、WG(j)是更新后的权值矩阵，η是学习速率.经过RBF网络学习后，网络的输出为

所以，控制律(2)改写为

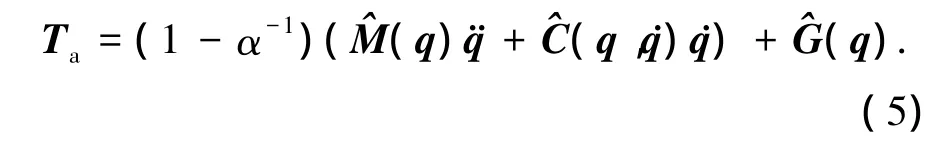
图6 RBF在线学习动力学模型的M(q)矩阵

控制框图如图7所示.

图7 在线学习动力学方程的SAC控制框图

4 Matlab仿真结果

图3所示的外骨骼主动自由度包括髋关节、膝关节，踝关节为被动自由度.根据临床步态实验［14］，一个步态周期内髋关节、膝关节的轨迹如图8，将获得的离散点拟合为时间t的(周期为2 s)方程:

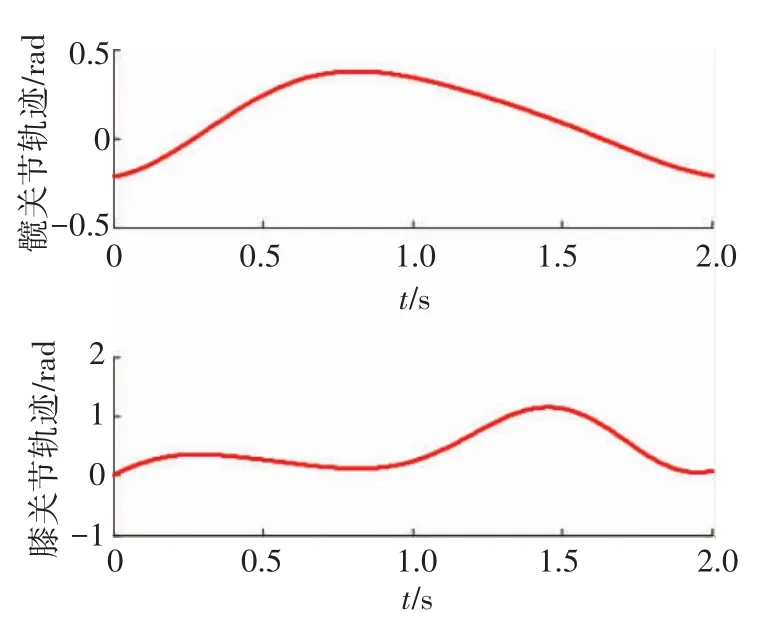
图8 人体临床步态髋关节、膝关节运动轨迹

取采样周期为Ts=0.001 s，0≤t≤2，应用控制律(5)，控制外骨骼机器人跟踪(6)所示的曲线，得到的跟随效果如图9.图9表明，外骨骼的关节轨迹与人体的行走轨迹基本吻合，实现了高度地跟随.跟随的误差曲线如图10，可以看出，误差在0的小邻域内变化，基本能够收敛到0.为了说明GA对RBF网络的作用，常规的RBF与优化后的RBF比较结果如图11、12所示.优化后的RBF网络跟踪误差更小，优化后的RBF网络SAC控制使得人机交互信息基本稳定地保持在0的小邻域内，人机交互信息的减小，表明了外骨骼能够高度跟随人体的运动轨迹.

图9 RBF在线学习SAC的人体轨迹跟踪

图10 RBF在线学习SAC的轨迹跟踪误差

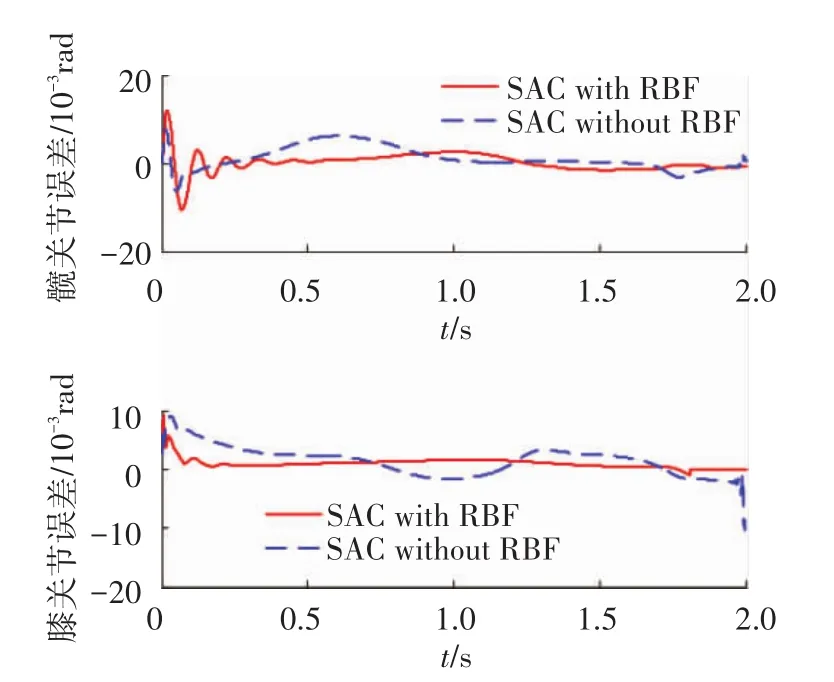
图11 人体轨迹跟踪误差对比曲线

图12 人机交互力矩对比曲线

5 结论

1)利用GA优化出满足适应度函数要求的RBF神经网络最佳中心矢量与基宽度，能够一定程度上改善RBF网络的映射能力.

2)设定的在线RBF学习过程只作权值的更新，通过设定的算法在线计算外骨骼机器人的动力学模型.

3)GA优化的RBF网络与没有优化的RBF网络的SAC控制比较表明，GA优化的RBF网络在跟随人体运动轨迹时有较高的精度以及较小的人机交互力矩.

4)基于GA优化的RBF网络学习外骨骼动力学模型的方法是可行的，实现SAC控制方法精确控制，但实际应用需要试验验证.

［1］KAZEROONI H，STEGER R，HUANG L.Hybrid control of the Berkeley Lower Extremity Exoskeleton(BLEEX)［J］.The International Journal of Robotics Research，2006，25(5/6):561-573.

［2］ZOSS A B，KAZEROONI H，CHU Andrew.Biomechanical design oftheBerkeleyLowerExtremityExoskeleton(BLEEX)［J］.IEEE/ASME Trans on Mechatronics，2006，11(2):128-138.

［3］ GHAN J，STEGER R，KAZEROONI H.Control and system identification for the Berkeley Lower Extremity Exoskeleton(BLEEX)［J］.Advanced Robotics，2006，20(9):989-1014.

［4］JIANG Z，ISHIDA T，SUNAWADA M.Neural network aided dynamic parameter identification of robot manipulators［C］//Proceedings of IEEE International Conference on Systems，Man and Cybernetics.Taipei:IEEE，2006:3298-3303.

［5］ BIDYADHAR S.DEBASHISHA J.Nonlinear system identification using memetic differential evolution trained neural networks［J］.Neurocomputing，2011，74(10):1696-1709.

［6］杨智勇，归丽华，杨秀霞，等.骨骼服神经网络灵敏度放大控制方法［J］.吉林大学学报:工学版，2009(3):824-829.

［7］ GHAN J，KAZEROONI H.System Identification for the Berkeley Lower Extremity Exoskeleton(BLEEX)［C］//Proceedings of IEEE International Conference on Robotics and Automation.Orlando:IEEE，2006:3477-3484.

［8］杨智勇，张远山，顾文锦，等.骨骼服灵敏度放大控制方法研究［J］.计算机仿真，2010(1):177-180.

［9］ WANG Hongfa，XU Xinai.Applying RBF neural networks and genetic algorithms to nonlinear system optimization［J］.Advanced Materials Research，2012，605-607:2457-2460.

［10］DING Shifei， XU LI， SU Chunyang， et al.An optimizing method of RBF neural network based on genetic algorithm ［J］. Neural Computing ＆Applications，2012，21(2):333-336.

［11］WANG Binli，BAI Guangliang，WEI Zhaolan.Bridge safety evaluation by RBF neural network with genetic algorithm［C］//Proceedings ofIEEE International Conference on Information and Financial Engineering(ICIFE).Chongqing:IEEE，2010:563-566.

［12］GE S S，HANG C C，WOON L C.Adaptive neural network control of robot manipulators in task space［J］.IEEE Trans on Industrial Electronics，1997，44(6):746-752.

［13］刘金琨.机器人控制系统的设计与MATLAB仿真［M］.北京:清华大学出版社，2008:31-158.

［14］KIRTLEY C.CGA normative gait database［DB/OL］.［2014-06-5］.http://www.clinicalgaitanalysis.com/data/.