机械弹性车轮随机振动理论与数值分析

赵又群，李小龙，张明杰，臧利国，李 波

(南京航空航天大学能源与动力学院，210016南京)

轮胎力学特性直接影响汽车整车的操纵稳定性和行驶平顺性等重要性能［1］.传统的橡胶充气轮胎力学模型主要分为理论模型和经验公式或半经验公式模型两大类［2］，现有轮胎理论模型主要有模态参数轮胎模型［3］、刚性环轮胎模型［4］、柔性环轮胎模型［5］、刷子轮胎模型［6］、综合分析轮胎模型［7］、统一轮胎模型［8］等.机械弹性车轮［9］是一种把橡胶轮胎和车轮集成一体的弹性车轮以往的理论模型不再适用于机械弹性车轮，而现有关于机械弹性车轮的研究都是基于二力杆模型进行的［10-11］，这种模型对于铰链组传力特性模拟不准确，故需要建立针对其自身特点的新的理论模型.

本文依据机械弹性车轮的结构和受力特点，建立适用于机械弹性车轮分析的弹性绳索简化模型.基于该模型进行随机不平路面激励下的振动分析，同时进行有限元仿真试验.

1 模型简介

1.1 机械弹性车轮结构及受力特点

机械弹性车轮结构如图1所示，主要由车轮轮毂、铰链组、复位弹簧和车轮外圈等组成.车轮外圈内部预埋弹性环骨架结构，由弹性组合卡将多股钢丝构成的多组弹性环锁卡在一起，起到骨架支撑作用且保证一定弹性，外部包裹橡胶形成胎面.车轮轮毂与车轮外圈通过等角度布置的12条铰链组连接，铰链组起到缓和冲击及传递转矩等作用，当铰链组变形后可通过复位弹簧回位.

图1 机械弹性车轮结构

机械弹性车轮承受来自不平路面的载荷激励时，通过车轮外圈和铰链组将载荷经轮毂传递给半轴，车轮外圈承载变形，起到支撑作用，而铰链组则拉直或压弯变形.当铰链组受拉时，与二力杆相似起到轴向传力作用;当铰链组受压时，则因绕铰接点转动弯曲变形而不承力.铰链组的这种单向传力性质，决定了机械弹性车轮不再适用现有充气轮胎的理论模型，故需建立新的适用于机械弹性车轮分析的理论模型.

1.2 模型假设条件

由于机械弹性车轮的材料、结构和运动过程相对复杂，故需要对其进行相应的简化，为了研究方便主要作如下假设:不考虑系统摩擦和阻尼作用的影响;车轮外圈作单层等效弹性圆环处理，轮毂作刚体处理;不考虑车轮外圈承载时小变形对铰链组布置角度的影响;不考虑转动和复位弹簧的作用.

1.3 建立简化模型

基于1.2节所述假设条件，建立机械弹性车轮的弹性绳索模型如图2所示.在图2(a)中，车轮外圈简化为等效刚度的单层弹性圆环，轮毂用刚性圆盘代替，而铰链组因其只受拉不受压的单向传力特性与弹性绳索相近，故将其简化为12根弹性绳索.由于轮毂自身重力相对整车重力等外加载荷较小，故忽略轮毂重力引起的上半部分各铰链组的初拉力及相应较小的弹性绳索预变形.图2(b)中车轮质量为m，随机不平路面输入激励位移为X1，轮毂中心响应位移为X2，车轮顶端响应位移为X3，弹性圆环的等效刚度为kr，机械弹性车轮上半部分弹性绳索总的等效刚度为ku，下半部分弹性绳索总的等效刚度为kd.由于不考虑铰链组布置角度变化的影响，同时考虑到结构的对称性，故

式中k0为半数弹性绳索总的传力等效刚度值.

图2 弹性绳索车轮模型

2 模型计算

2.1 单根弹性绳索刚度

杨氏模量定义:

式中:应力σ=F/A，F为轴向力，A为有效横截面积;应变ε=Δl/l，l为原长，Δl为长度变化量.

刚度定义:

由式(1)和(2)联立解得刚度与杨氏模量的关系为

若已知铰链组材料的杨氏模量和其有效截面积及长度，则可根据式(3)计算得到单根弹性绳索对应的刚度值kl.

2.2 上下总等效刚度

图3为机械弹性车轮的弹性绳索模型中的弹性绳索总等效刚度k0分析计算示意，假设图3(a)中机械弹性车轮的铰链组处于初始位置，当机械弹性车轮的铰链组顺时针(或逆时针)绕车轮轮毂中心旋转θ=π/12，时即到达铰链组的终止位置，这里以顺时针为例，如图(b)所示，则由机械弹性车轮的结构对称性可知，用θ∈［0，π/12］这个区间就可以表述机械弹性车轮在任何阶段下的位置状态.例如铰链组从图3(a)所示位置绕车轮轮毂中心旋转π/12后，铰链组12到达铰链组1的位置，铰链组1到达铰链组2的位置，以此类推，但此时的承载状态则与初始位置的承载状态相同.那么，只需分析θ∈［0，π/12］这个区间内的机械弹性车轮的弹性绳索模型中的上下部分弹性绳索的总等效刚度即可以得到任意时刻的k0值.

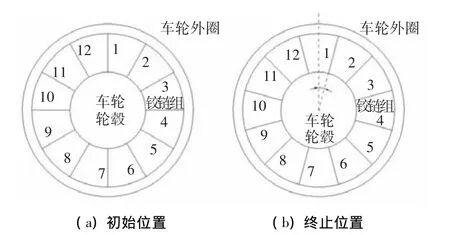
图3 弹性绳索等效刚度分析计算示意

当θ=0时，机械弹性车轮处于初始位置，水平的弹性绳索对垂直方向没有刚度作用，则

式中kl为单根弹性绳索的刚度值.

当0＜θ≤π/12时，由铰链组布置的几何关系得

式(4)满足式(5)，故弹性绳索总等效刚度k0可由式(5)计算得到.

2.3 频率响应函数

弹性绳索模型的系统运动学方程:

当随机不平路面激励信号X1＞0时，ku=k0，kd=0，式(6)变为

由式(7)可得微分方程

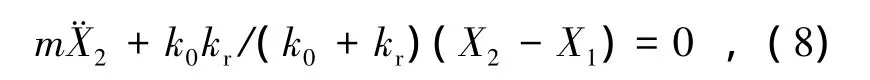
对式(8)两边进行傅里叶变换，解得

式中:K=k0kr/(k0+kr).

当随机不平路面激励信号X1＜0时，ku=kd=k0，式(6)变为

由式(9)可得微分方程

对式(10)两边进行傅里叶变换，解得

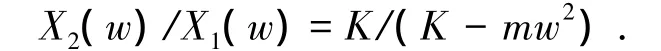
式中:K=(k0(k0+2kr))/(k0+kr).

综上可得，机械弹性车轮的弹性绳索简化模型的频响函数为

式中:

2.4 响应功率谱密度

根据随机振动分析理论［12］，由维纳-辛钦关系式可得频率域内的双边功率谱密度，但对于机械弹性车轮只有正值频率是有效的，故应计算其单边功率谱.若随机不平路面的激励谱为SX(w)，则其响应功率谱为

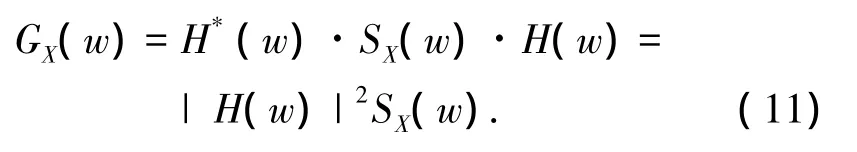
式中:H*(w)为H(w)的共轭转置，|H(w)|为H(w)的模.

3 随机振动分析

3.1 随机不平路面输入

根据三角级数法［13］构建随机不平路面的输入激励，按采样定理和三角级数叠加模型选定相应的仿真参数，编写Matlab程序后生成C级随机路面激励如图4所示.

图4 C级随机路面激励

3.2 弹性绳索模型参数

车轮质量m=50 kg，根据有限元仿真试验结果，取弹性圆环的等效承载刚度kr=5×105N/m，单根弹性绳索的有效刚度通过式(3)计算，带入

分别计算车轮处于初始位置和终止位置时的k0，然后取均值近似替代弹性绳索总等效刚度值.当车轮处于初始位置时，θ=0，由式(5)得

当车轮处于终止位置时，θ=π/12，由式(5)得

取均值有

3.3 随机振动响应

根据弹性绳索模型参数等，计算得到机械弹性车轮在C级随机路面激励下的位移响应(如图5所示)，从图中可以看出轮毂中心响应位移的走势与路面激励的走势相近，说明响应结果合理.

对于位移响应可通过时域信号变换得响应功率谱密度为|FFFT(X)|2/N，FFFT为快速傅里叶变换，N为采样点数.

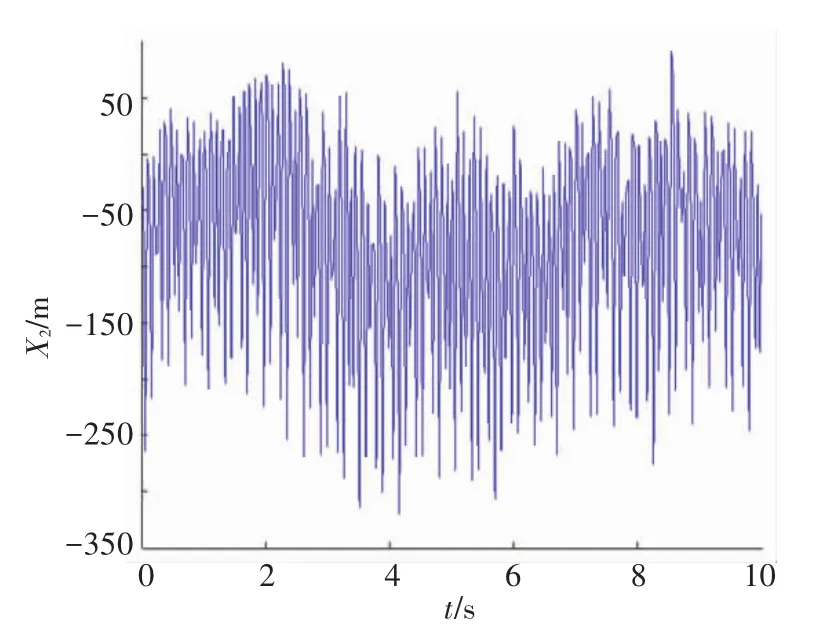
图5 轮毂中心位移响应

同时，也可根据式(11)计算得到其响应功率谱.

按数学模型计算得到的机械弹性车轮在C级随机路面激励下的响应谱如图6所示，图中实线为轮毂中心位移响应时域信号经快速傅里叶变换得到的响应功率谱密度曲线，虚线为按式(11)频率响应函数计算得到的响应功率谱密度曲线.对比两种方式得到的功率谱密度响应曲线可以看出，虽然两条响应曲线的响应峰值不同，但对应的响应频率值基本重合，这说明计算得到的共振频率是合理的.当机械弹性车轮在C级路面工作，频率达到11 Hz和19 Hz左右时容易发生共振，从而对机械弹性车轮造成破坏.

图6 轮毂中心位移响应功率谱

3.4 有限元仿真

按前述机械弹性车轮模型建立有限元仿真简化模型如图7所示，铰链组用12根弹簧模拟，单根弹簧刚度值取kl，设定相应材料参数［14-15］如表1，机械弹性车轮与地面间为摩擦接触.摩擦系数μf=0.6，其他为绑定接触.输入边界条件为地面，采用相同随机路面输入信号，对摩擦接触非线性求解，设定求解算法为增广拉格朗日算法.其他线性接触采用罚函数法求解，同时设置合适的载荷步、载荷子步及时间步，然后整体采用迭代法进行有限元计算，在ANSYS/Worckbench中进行随机振动分析，得到轮毂位移功率谱密度响应结果如图8所示.

图7 弹性绳索有限元模型

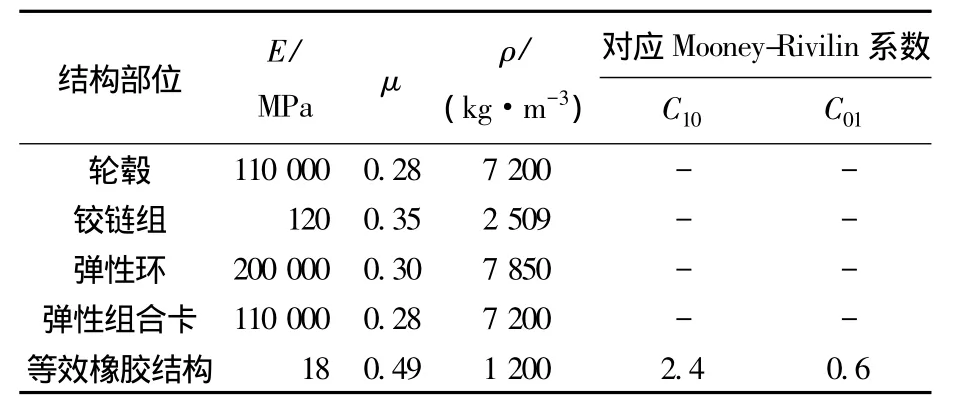
表1 机械弹性车轮材料属性

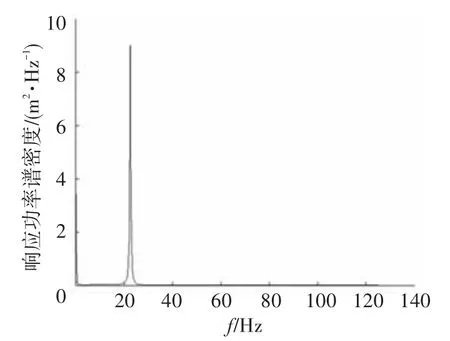
图8 有限元仿真响应功率谱

从图8中可以看出，在相同C级随机路面输入条件下，有限元仿真得到的机械弹性车轮共振频率为21 Hz左右.对比理论数学模型计算结果可以看出，对于理论计算得到的11 Hz共振频率在进行有限元仿真时产生的幅值相对较小，这是由于机械弹性车轮在进行有限元仿真时铰链组所处位置、车轮变形时铰链组布置角度变化和车轮外圈的材料及几何非线性因素的影响造成的，即:理论计算模型总等效刚度是采用初始位置刚度和终止位置刚度的均值代替计算的，反映的是机械弹性车轮工作中的一般情况，而有限元仿真则是进行的初始位置的仿真试验，是特定位置的仿真结果;理论计算模型没有考虑车轮变形时铰链组布置角度变化的影响，其上、下总等效刚度是近似计算的，而有限元仿真时则考虑了弹簧布置角度变化的影响;另外，车轮外圈结构在进行有限元仿真时的材料非线性和几何非线性因素在理论计算时是将其简化为一个单层弹性圆环并用线性的等效刚度近似代替计算的，存在一定偏差.以上这些因素的作用使得理论计算和仿真计算时的刚度存在差异，从而导致在11 Hz时仿真幅值较小.但理论计算得到的19 Hz共振频率，与21 Hz的仿真共振频率接近，说明了理论模型的正确性，验证了建立的弹性绳索理论模型的合理有效性.另外，从图6和图8的结果可以看出，机械弹性车轮在C级随机路面工作时，应主要避免19～21 Hz这一频段，以免发生共振对机械弹性车轮造成破坏.

4 结论

1)依据机械弹性车轮的结构和承载特点，针对铰链组只受拉不受压的单向传力特性，提出了适用于机械弹性车轮振动分析的弹性绳索模型，并推导了该模型的数学表达式、等效刚度表达式以及频响函数;

2)基于弹性绳索模型进行了C级随机不平路面输入激励下的随机振动分析，得到了机械弹性车轮轮毂中心时域内位移响应和频域内的功率谱密度响应曲线，并通过对比有限元仿真分析结果验证了所提出的弹性绳索模型的正确性.

3)机械弹性车轮工作时应主要避免19～21 Hz频率区段，以免发生共振对机械弹性车轮造成破坏，为机械弹性车轮的设计和优化提供了指导.

［1］庄继德.现代汽车轮胎技术［M］.北京:北京理工大学出版社，2001.

［2］李松焱，闵永军，王良模，等.轮胎动力学模型的建立与仿真分析［J］.南京工程学院学报:自然科学版，2009，7(3):34-38.

［3］FAN Chengjian，GUAN Dihua.Tire modeling for vertical properties including enveloping properties using experimental modal parameters［J］.Vehicle System Dynamics，2003，40(6):419-433.

［4］郭孔辉，吴海东，卢荡.轮胎垂直方向刚性环模型［J］.科学技术与工程，2007，7(4):556-559.

［5］VU T D，DUHAMEL D，ABBADI Z，et al.Dynamic analysis of a tire using a nonlinear Timoshenko ring model［C］//Proceedings of ISMA:Int Conf Noise Vibr，Eng.Leuven:Katholieke Universiteit Leuven，2012:1629-1640.

［6］SVENDENIUS J，GAFVERT M，BRUZELIUS F，et al.Experimental validation of the brush tire model 5［J］.Tire Science and Technology，2009，37(2):122-137.

［7］KIM S，NIKRAVESH P E，GIM G.A two-dimensional tiremodelon uneven roads forvehicle dynamic simulation 1［J］.Vehicle system dynamics，2008，46(10):913-930.

［8］LU Dang，GUO Konghui.UniTire steady state model:overview and applications［C］//2011 3rd International Conference on Advanced Computer Control.Harbin:IEEE，2011:341-345.

［9］汪伟，赵又群，黄超，等.新型机械弹性车轮的建模与通过性研究［J］.中国机械工程，2013，24(6):724-729.

［10］WANG Wei，ZHAO Youqun，WANG Jian，et al.Structure analysis and ride comfort of vehicle on new mechanical elastic tire［C］//Proceedings of the FISITA 2012 World Automotive Congress.Berlin:Springer，2013:199-209.

［11］汪伟，赵又群，姜成，等.基于新型机械弹性车轮的整车平顺性分析［J］.中国机械工程，2013，24(22):3114-3117.

［12］LU F，KENNEDY D，WILLIAMS F W，et al.Symplectic analysis of vertical random vibration for coupled vehicle:track systems［J］.Journal of Sound and Vibration，2008，317(1):236-249.

［13］陈春俊，李华超.频域采样三角级数法模拟轨道不平顺信号［J］.铁道学报，2006，28(3):38-42.

［14］NARASIMHAN A，ZIEGERT J，THOMPSON L.Effects of material properties on static load-deflection and vibration of a non-pneumatic tire during high-speed rolling［J］.SAE International Journal of Passenger Cars-Mechanical Systems，2011，4(1):59-72.

［15］KIM K，KIM D M.Contact pressure of non-pneumatic tires with hexagonal lattice spokes［C］//SAE 2011 World Congress ＆ Exhibition.Detroit: SAE International，2011:01-0099.