平衡时溶液的表面吸附

陈飞武 卢 天 武 钊

(北京科技大学化学与生物工程学院化学与化学工程系,北京 100083;功能分子与晶态材料科学与应用北京市重点实验室,北京 100083)

平衡时溶液的表面吸附

陈飞武*卢 天 武 钊

(北京科技大学化学与生物工程学院化学与化学工程系,北京 100083;功能分子与晶态材料科学与应用北京市重点实验室,北京 100083)

溶液的表面吸附仍是表面热力学当中的一个具有挑战性的问题.在本文中我们定义了一个新的热力学态函数,表面吸附的平衡条件是这个态函数的微分为零.基于这个条件,我们推导了描述平衡时表面吸附的新方程.在推导过程中没有采用假想分界面.新的表面吸附方程和Gibbs表面吸附方程完全不一样.还通过分子动力学方法模拟了氯化钠溶液,模拟结果和我们的理论预测符合较好.

表面吸附; 平衡条件; 吉布斯吸附方程; 热力学态函数; 溶液

1 Introduction

It is well known that,for a cup of sugar water,the very thin surface layer of the sugar water will be sweeter than its interior part.Though many progresses have been made so far,1–6yet interpreting this interesting phenomenon quantitatively is still a challenging problem in the thermodynamics of surfaces.For a multicomponent solution,one usually start with the differential form of the Gibbs free energy as follows7

where S,T,P,V,γ,σ,µB,and nBare the system's entropy,temperature,pressure,volume,surface tension,surface area,chemical potential and the number of moles of the component B,respectively.The third term on the right hand side of Eq.(1) is the surface work.Since the surface area could not increase by itself in most cases and could only be stretched out by its surr-ounding environment,the surface work has a positive sign.The chemical potential of the component B(µB) in a nonelectrolyte solution has the following form

where v=v++ v–.If the surface and bulk phases are considered,Eq.(1) should be expressed explicitly as

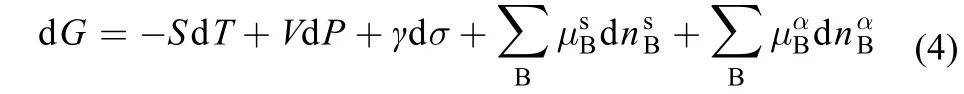
where the superscripts “s” and “α” are referred to the surface and bulk phases,respectively.

It is well known qualitatively that the concentrationin the surface region will be bigger than the concentrationin the bulk region if the surface tension decreases with,and vice versa.Since there is no term in Eq.(4) related to the change of the surface tension,Gibbs exploited an analog form of the Gibbs-Duhem equation at constant temperature and pressure to explain these absorption behaviors,which is

where Γ21,the surface excess of the component B relative to the solvent A,is defined as

Eq.(6) is only valid for a two-component solution.Recently Menger et al.8–10found experimentally for some systems that the right-hand side of Eq.(6) remained almost unaltered while the surface excess Γ21on the left hand side of Eq.(6) still changed with the concentration of the component B,which led to the arguments on the Gibbs analysis.11–13

2 Theory

Based on the facts above,we started to rethink the thermodynamics of surfaces from beginning.It is well known that a change of the concentration of a component B in the surface region due to the surface absorption will lead to changes of the surface tension and the corresponding surface work as shown in Eqs.(1) and(4).Contrary to the surface works in the most cases,this type of the surface work is not done externally by the surrounding environment,but done by the system itself.Therefore,we think that this internal surface work should be –γdσ instead of γdσ as presented in Eqs.(1) and(4).This is the key starting point in the present work.For simplicity and convenience of discussions below,only Eq.(4) is rewritten as

If γdσ is substituted with d(γσ)–σdγ,Eq.(8) can be expressed as

where F is defined as

As will be discussed below,the equilibrium condition of the surface absorption is that the differential of this thermodynamic state function F is zero at constant temperature and pressure.From Eq.(9),the differential form of the chemical potential in the surface phase can be derived

where SB,m,VB,m,and σB,mare the partial molar entropy,partial molar volume,and partial molar surface area,respectively.In comparison with Eq.(8),the third term on the right hand side of Eq.(9) is directly related to the change of the surface tension,as we expect.The total differential form of the surface tension is written as

provided that the temperature and pressure remain constant.Substituting Eq.(12) into Eq.(9) leads to

Since the total amount of moles of the component B,nB=,in the surface and bulk regions are fixed,therefore.With this equality Eq.(13) becomes

At constant temperature and pressure the equilibrium condition dF=0 results in the following equation

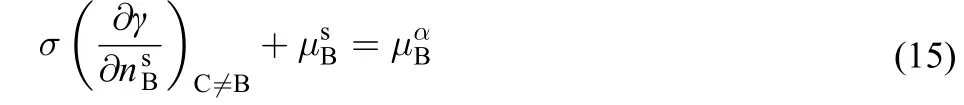
It is seen clearly from Eq.(15) that the chemical potentials inthe surface and bulk phases are not equal.Substituting the expressions ofandin the Eq.(2) or Eq.(3) into Eq.(15),we finally obtain

where ζ will be 1 or v if the solute is a nonelectrolyte or electrolyte,respectively.In the above derivation,the standard chemical potentials in the surface and bulk phases are considered to be equal.It is shown from Eq.(16) thatwill be bigger thanif the derivative of the surface tension withis negative,and vice versa.This is in accordance with the surface absorption behavior of the component B in a solution.

If the solution is very dilute the chemical potentials of the solvent in the surface and bulk phases can be regarded to be approximately equal.Then we get another equation to describe the relationship between the surface tension and the chemical potentials of the solute,i.e.,

provided that σB,mremains approximately constant.γ0is the surface tension of the pure solvent.Substituting the expressions ofandin Eq.(2) or Eq.(3) into Eq.(17) leads to

Eqs.(17) and(18) are valid only for a two-component solution.Eq.(18) has also been derived and discussed previously by Nath,14Li15and Yu16et al.

3 Results and discussion

In order to test the validity of Eq.(16),molecular dynamic simulations of aqueous sodium chloride solutions have been performed.As will be clear below,the reason to choose aqueous sodium chloride solutions is that these solutions have similar absorption behaviors as observed by Menger et al.8–10First a rectangular box with dimensions of 4 nm × 4 nm × 8 nm was set up and about 4200 water molecules were filled into the center of the box to yield a 8 nm-thick water layer.Then some water molecules were replaced with Na+and Cl–ions.Totally 10 s·ystems with NaCl concentrations ranging· from 0.2 to 2.0 molL–1with increment step of around 2.0 molL–1were investigated.The simulation box was extended in both sides to yield two 4 nm thick vacuum layers.Therefore the final size of simulation box is 4 nm × 4 nm × 16 nm.Gromacs program17,18was employed for simulations at constant volume and temperature.The temperature was maintained at 300 K via Nosé-Hoover thermostat.19,20Kirkwood-Buff force field21,22and SPC/E model23were used to represent NaCl and water,respectively.The water geometry was constrained with SETTLE technique.24Long range electrostatic interactions were evaluated by the Particle Mesh Ewald(PME) approach,25and van der Waals interactions were truncated at the cut-off distance of 0.14 nm.The surface tensions were calculated by26

where Lzis the length of the box in the z direction which is normal to the surface,the Pxx,Pyy,and Pzzare the diagonal components of the pressure tensor.

Ten ionic concentration distribution curves are presented in Fig.1.The thickness of a surface layer is determined as the distance at z direction with the density of NaCl starting from zero to the density in bulk.As can be seen from the figure,the surface layers of the above systems are all approximately 0.8 nm thick.One snapshot of molecular dynamic trajectory is presented in Fig.2 to illustrate the distributions of NaCl in solution during the simulation.It is a side view of the whole simulation box.

Fig.1 Ten density profiles(ranging from 0.2 to 2.0 mol·L–1with incremental size of 2.0 mol·L–1) of NaCl with respect to the distance in z directionN:number density of Nacl pairs

Fig.2 Snapshot of molecular dynamic trajectory in simulation

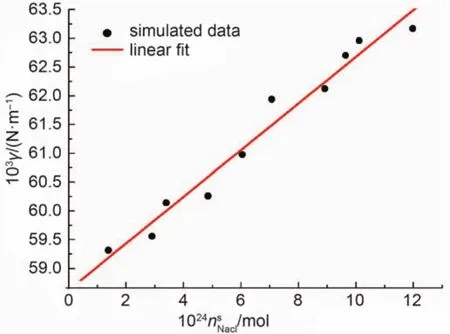
Fig.3 Simulated surface tension versus the number of moles of NaCl in the surface region

The plot of the simulated surface tension(γ) versus the number of moles of NaCl in the surface region() is shown in Fig.3.It can be seen from Fig.3 that the surface tension increases asbecomes larger.These data were then fitted to a straight line:·.The interception value of 58.607 × 10–3Nm–1corresponds to the pure water surface tension.Though it is in good agreement with recent molecular dynamic simulation,26yet the simulated surface tension of pure SPC/·E water is lower than the experimental value of 71.6 × 10–3Nm–1because no long-range dispersion correction is included.Linear correlation coefficient and root mea·n square deviation of the fitting are 0.984 and 0.277 × 10–3Nm–1,respectively.This linear behavior in the sodium chloride solution was also observed in the other research works.26–28Because of the good linear correlation of the simulated data and also the difficulty to calculate the derivativeby the molecular dynamic simulation,the derivative value of 0.405 × 1021N·m–1·mol–1is directly taken from the fitting and will be used below to calculate the gas constant R in Eq.(16).

The plot of the simulated concentration of NaCl in the bulk region versus the concentration of NaCl in the surface region is shown in Fig.4.These data were also fitted to a line2.4806csNaCl-0.0590.The linear correlation coefficient and the root mean square deviation are 0.99602 and 0.06454,respectively.The ratio ofcan be regarded approximately to be 2.4806 because of the interception value(–0.0590) of the fitted line with the axis ofclose to zero.This ratio is also considered approximately as the value of.The reason that the fitted line in Fig.4 passes slightly away from the original point is perhaps due to the numerical noise of molecular dynamic simulation.

On the other hand,the derivative of the surface tension γ with respect toin the surface phase on right hand side of Eq.(6) is close to a constant,but the surface excess Γ21on the left hand side of Eq.(6) still changes with.This is similar to the experimental observations made by Menger et al.8–10Therefore,it is expected that Eq.(16) may be exploited to solve the problems in the works of Menger et al.

Fig.4 Simulated concentration of NaCl in the bulk region versus concentration of NaCl in the surface region

4 Conclusions

A new thermodynamic state function F is defined to describe the thermodynamics of surfaces.The equilibrium condition of the surface absorption of a solution is that dF=0.Based on this,a new absorption equations such as Eq.(16) are derived.Molecular dynamic similations of aqueous solutions of sodium chloride are in good agreement with our theoretical analysis.Instead of Gibbs absorption equation,it is hopeful that Eq.(16) may be a promising alternative to solve the problems found by Menger et al.8–10

Acknowledgment:The authors are very grateful to Prof.LI Le-Min of Peking Univeristy for his valuable discussion.

(1)Cheng,X.H.;Zhao,O.D.;Zhao,H.N.;Huang,J.B.Acta Phys.-Chim.Sin.2014,30,917.[程新皓,赵欧狄,赵海娜,黄建滨.物理化学学报,2014,30,917.] doi:10.3866/PKU.WHXB201403191

(2)Hu,S.Q.;Ji,X.J;Fan,Z.Y.;Zhang,T.T.;Sun,S.Q.Acta Phys.-Chim.Sin.2015,31,83.[胡松青,纪贤晶,范忠钰,张田田,孙霜青,物理化学学报,2015,31,83.] doi:10.3866/PKU.WHXB201411191

(3)Wang,K.;Yu,Y.X.;Gao,G.H.J.Chem.Phys.2008,128,185101.doi:10.1063/1.2918342

(4)Peng,B.;Yu,Y.X.J.Chem.Phys.2009,131,134703.doi:10.1063/1.3243873

(5)Ghosh,S.;Roy,A.;Banik,D.;Kundu,N.;Kuchlyan,J.;Dhir,A.;Sarkar,N.Langmuir 2015,31,2310.doi:10.1021/la504819v

(6)Bera,M.K.;Antonio,M.R.Langmuir 2015,31,5432.doi:10.1021/acs.langmuir.5b01354

(7)Atkins,P.;de Paula,J.Atkins' Physical Chemistry,7th Ed.;Oxford University Press:Oxford,2002.

(8)Menger,F.M.;Shi,L.;Rizvi,S.A.A.J.Am.Chem.Soc.2009,131,10380.doi:10.1021/ja9044289

(9)Menger,F.M.;Shi,L.;Rizvi,S.A.A.Langmuir 2010,26,1588.doi:10.1021/la9043914

(10)Menger,F.M.;Rizvi,S.A.A.Langmuir 2011,27,13975.doi:10.1021/la203009m

(11)Laven,J.;de With,G.Langmuir 2011,27,7958.doi:10.1021/la200152d

(12)Menger,F.M.;Rizvi,S.A.A.;Shi,L.Langmuir 2011,27,7963.doi:10.1021/la201219g

(13)Li,P.X.;Li,Z.X.;Shen,H.H.;Thomas,R.K.;Penfold,J.;Lu,J.R.Langmuir 2013,29,9324.doi:10.1021/la4018344

(14)Nath,S.J.Colloid Interface Sci.1999,209,116.

(15)Li,Z.B.;Li,Y.G.;Lu,J.F.Ind.Eng.Chem.Res.1999,38,1133.doi:10.1021/ie980465m

(16)Yu,Y.X.;Gao,G.H.;Li,Y.G.Fluid Phase Equilibr.2000,173,23.doi:10.1016/S0378-3812(00)00396-4

(17)Gromacs Program,Version 4.6.5.http://www.gromacs.org(accessed on Sep 14,2014).

(18)Hess,B.;Kutzner,C.;van der Spoel,D.;Lindahl,E.J.Chem.Theory Comput.2008,4,435.doi:10.1021/ct700301q

(19)Hoover,W.G.Phys.Rev.A 1985,31,1695.doi:10.1103/ PhysRevA.31.1695

(20)Nosé,S.Mol.Phys.1984,52,255.doi:10.1080/00268978400101201

(21)Weerasinghe,S.;Smith,P.E.J.Chem.Phys.2003,119,11342.doi:10.1063/1.1622372

(22)Ploetz,E.A.;Bentenitis,N.;Smith,P.E.Fluid Phase Equilib.2010,290,43.doi:10.1016/j.fluid.2009.11.023

(23)Berendsen,H.J.C.;Grigera,J.R.;Straatsma,T.P.J.Phys.Chem.1987,91,6269.doi:10.1021/j100308a038

(24)Miyamoto,S.;Kollman,P.A.J.Comput.Chem.1992,13,952.

(25)Darden,T.;York,D.;Pedersen,L.J.Chem.Phys.1993,98,10089.doi:10.1063/1.464397

(26)Chen,F.;Smith,P.E.J.Phys.Chem.B 2008,112,8975.doi:10.1021/jp711062a

(27)Jarvis,N.L.;Scheiman,M.A.J.Phys.Chem.1968,72,74.doi:10.1021/j100847a014

(28)Weissenborn,P.K.;Pugh,R.J.Langmuir 1996,11,1422.

Surface Absorption of a Solution at Equilibrium

CHEN Fei-Wu*LU Tian WU Zhao
(Department of Chemistry and Chemical Engineering,School of Chemistry and Biological Engineering,University of Science and Technology Beijing,Beijing 100083,P.R.China; Beijing Key Laboratory for Science and Application of Functional Molecular and Crystalline Materials,Beijing 100083,P.R.China)

Surface adsorption of a solution is still a challenging problem in the thermodynamics of surfaces.In this work,a new thermodynamic state function is defined.The equilibrium condition of surface adsorption is that the differential of this state function is equal to zero.Based on this condition,we derived a new equation to describe surface adsorption at equilibrium.No hypothetical dividing surface is needed in this derivation.The new equation is quite different from the Gibbs adsorption equation.We also performed molecular dynamic simulations of aqueous sodium chloride solutions.The simulated results are in good agreement with our theoretical predictions.

Surface absorption; Equilibrium condition; Gibbs absorption equation; Thermodynamic state function; Solution

March 4,2015;Revised:June 19,2015;Published on Web:June 19,2015.

O641

icle]

10.3866/PKU.WHXB201506191 www.whxb.pku.edu.cn

*Corresponding author.Email:chenfeiwu@ustb.edu.cn.

The project was supported by the National Natural Science Foundation of China(21173020,21473008).国家自然科学基金(21173020,21473008)资助项目

© Editorial office of Acta Physico-Chimica Sinica