关于完善基本养老金计发办法的思考

文/徐方根

关于完善基本养老金计发办法的思考

文/徐方根

本文在坚持“统账结合”这一具有中国特色基本养老保险制度模式的基础上，针对现行企业职工基本养老金计发办法的缺点进行制度创新，提出“黄金分割”指数模型，以适应更大档次区间的缴费及待遇计算。同时，借鉴该数学模型设计出基于替代率的基本养老金待遇调整方法，从而完善基本养老金的计发办法和待遇调整方法。

现行基本养老金计发办法存在缺点。2005年国务院发布《关于完善企业职工基本养老保险制度的决定》，改革基本养老金计发办法。计发办法改革后，各地基础养老金和个人账户养老金计发公式大体一致，基础养老金计发基数是本人指数化月平均缴费工资和当地上年度在岗职工月平均工资的平均值。改革后的基础养老金计发基数相当于对平均缴费工资指数做了一次类似于Y=（1+X）/2的线性变换。但从全国来看，基本养老金计发办法并不完全统一。例如平均指数计算，有采用包含视同缴费年限的“全程指数”（包括视同缴费年限段和实际缴费年限段的“大指数”），也有仅采用缴费年限段的“缴费指数”（称为“小指数”）。过渡性养老金计发基数也有差异，有的采用“双基数”，即将指数化省平工资与上年省平工资相加再除以2作为计发基数；有的则直接将指数化省平工资作为计发基数。

此外，相对之前不论缴费高低、长短，基础养老金均按上年全省在岗职工月平均工资的20%（Y=X0×20×1%）计发，算法上虽有很大改进，但这种线性函数存在很大缺点：因为其最小截距已高达0.5，不能解决更低档次缴费及待遇计算问题。从长远来看，这种算术平均算法既不够严谨也不太科学。要更加注重并发挥社会保障再分配作用，更加注重公平公正，就必须改革完善现行计发办法，用方法创新和思维创新，改变传统的线性模式，用更优化的数学模型来解决复杂的养老金计发问题。

完善基本养老金计发办法的具体思考。综观几次计发办法改革，从最初的绝对平均到过度强调激励机制，指数优化在0和1之间走了两个极端，那么，在0-1区间取什么值才是最优呢？社保领域是否也存在天然的黄金分割点呢？经过多年的反复测算和分析，笔者发现了一个比线性回归模型更优的非线性幂函数模型：Y=X0.618（0.618为黄金分割点），可兼容更低档次（指数0.6以下）缴费及待遇计算问题，并与现行办法几乎完全契合。具体见下图：

引入黄金分割指数模型，新的基本养老金计发公式为：

月基本养老金=基础养老金+个人账户养老金+过渡性养老金（中人）

基础养老金=本人黄金分割指数化月平均缴费工资×累计缴费年限×1%

其中，本人黄金分割指数化月平均缴费工资=本人加权平均缴费工资指数0.618×当地上年度在岗职工月平均工资

加权平均缴费工资指数=

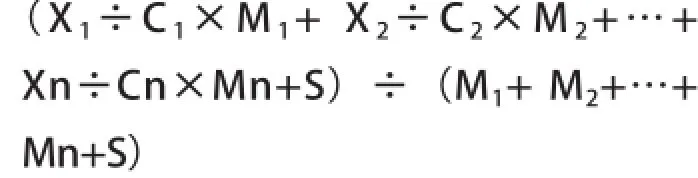
其中：X为当年本人月平均缴费工资

M为当年本人实际缴费月数

C为上一年全省在岗职工月平均工资

S为1996年前累计缴费月数（含视同缴费月数）

备注：当n为一次性趸缴（或预缴）时，“ Xn÷Cn”为缴费时选择的缴费档次，Mn为缴费月数。

个人账户养老金=退休时个人账户储存额÷本人退休年龄相对应的计发月数

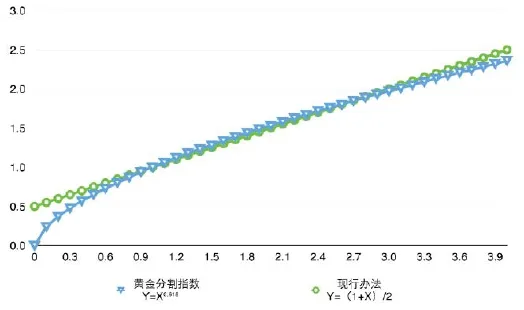
指数优化数学函数模型比较图

过渡性养老金=过渡系数×本人黄金分割指数化月平均缴费工资×过渡计发年限×1%

设缴费指数为a，通过改造和完善，a的适用范围扩展到［0，4］（即0≤a ≤4）的区间，对低收入群体和高收入群体均有所照顾。假如a=0，则“新人”退休时，待遇计发时仅有个人账户养老金，与城乡居民养老保险制度接轨；当a在［0，0.6］（即0≤ a≤0.6）区间内的，也可以进行缴费，按照统一的“黄金分割”模型进行待遇计发，包含基础养老金、个人账户养老金；当 a为0.6、0.7、0.8、0.9，基础养老金水平分别低于38号文计发办法8.84%、5.63%、3.20%、1.37%，有利于督促该群体提高缴费；当 a在［1，2.6］ （即1≤ a≤ 2.6）范围，基础养老金水平会略高于38号文计发办法1%到2.85%，对缴费水平略高于在岗职工平均工资的进行略微增长；当 a在［2.6，3.5］ （即2.6≤ a≤ 3.5）的范围，基础养老金水平降幅控制在4%以内；当a在［3.5，4］ （即3.5≤ a≤4）的范围，基础养老金水平降幅控制在6%以内，对高收入群体待遇进行适当控制，体现制度再分配职能。

完善计发办法的延伸思考。基本养老金的调整政策应该是普调与特调相结合，下面仅对普调政策加以论述。应建立起与缴费水平相挂钩的正常调整机制，可以借鉴计发办法相关数学模型，先对退休人员的替代率（个人养老金与全省月平均工资之比）进行压缩优化，再乘以测算出的调整基数（以省为单位测算），具体普调公式如下：

个人普调金额=压缩优化｛本人替代率｝×调整基数

=（本人替代率）a×｛平均养老金×普调幅度/AVG〔POWER（替代率，a）〕｝

其中a为优化指数，取值范围为：0≤a≤1。当a=0时，所有人按同一标准定额调整；当a=1时，所有人按同一幅度等比例调整。当a=1/3时为三次方根优化，a=1/2时为二次方根优化，当a=0.618时为黄金分割优化。这里以三次方根优化为例，对部分退休人员数据进行模拟测算，结果如下：

假定某省月平工资为3500元，平均养老金为1500元，普调幅度为10%，则通过测算可得：

调整基数=平均养老金×普调幅度/AVG〔POWER（替代率，a）〕

=1500×10%×AVG〔POWER（替代率，1/3）〕≈200

假定最低养老金为500元，最高养老金为10000元，根据普调数学公式可得：

T500=（500/3500）1/3×200=105，T10000=（10000/3500）1/3×200=284

通过以上办法，养老金水平差距高达20倍，但其最终的调待结果差距仅在3倍以内，且按同一标准的数学模型实现连续平滑调整。该办法有利于建立统一的调待机制，个人普调金额与本人替代率挂钩，养老金偏低的绝对调整金额小，但调整幅度相对大；养老金偏高的绝对调整金额大，但调整幅度相对小，兼顾了公平与效率问题。优化指数可灵活设置，指数小更体现公平原则，指数大则更讲究效率，可在国家规定的范围内，各省结合自己的实际情况和具体测算数据灵活把握。

完善基本养老金计算办法的意义。引入黄金分割指数模型的养老金计发办法，既满足低收入群体参保缴费的需求，又解决了调节收入分配的科学性问题。同时，将黄金分割指数模型应用到基本养老金待遇调整，可以充分利用其优良的压缩调节作用，完善普调政策，有利于建立统一的调待机制，补齐养老保险制度短板。

作者单位：四川省社会保险管理局

本刊与中国医师协会联袂举办“医院・医师・医保—医保管理研讨会”

2015年，深化医改措施频现，医疗保险付费方式改革和加强医疗服务监管亦向纵深发展。医师作为医疗服务的提供者，如何成为健康的守护人和医保基金的“守门人”，如何为参保人员提供合理必要的医疗服务，至关重要。9月12日，由中国医师协会主办、中国社会保障杂志社协办的 “医院·医师·医保—医保管理研讨会”在云南昆明举办，研讨会就公立医院改革、医师参与医保付费方式改革、医疗服务监管等热点问题展开交流研讨。（春红）