无限区域二维势流直接边界元法精度分析

韩玉超，卢晓平，王　中海军工程大学舰船工程系，湖北武汉430033

无限区域二维势流直接边界元法精度分析

韩玉超，卢晓平，王中
海军工程大学舰船工程系，湖北武汉430033

边界元法作为一种重要的数值方法已在许多领域得到广泛应用，但在船舶水动力势流理论数值计算方面，有关直接边界元法的研究并不充分，尤其是在船舶兴波阻力势流理论求解方面，以往的“面元法”通常是基于Hess-Smith法的间接法，这类方法在理论和数值计算上都存在着缺陷。针对船舶水动力势流理论计算，采用直接边界元法，对二维势流无界绕流算例进行系统的数值计算，并根据二维势流问题的计算结果详细探讨边界单元离散形式和单元上的数值积分方法对计算精度的影响，各项数值计算均以Matlab软件编程实现。结果表明，采用常数单元和龙贝格积分法能够得到较准确的结果，且计算速度较快。

直接边界元法；势流理论；边界离散；数值积分

0　引言

根据边界积分方程中未知函数的不同，边界元法可分为直接法和间接法2种。在以往的船舶兴波阻力势流理论问题求解方面，通常是采用基于Hess-Smith法的间接法［1］。在间接法中，边界积分方程中的未知函数并不是待定函数本身，而是作用于所考察区域边界相应线（面）上的某种虚拟的分布量，由于待定函数是通过求出虚拟分布量后间接求出，且没有严格的数学定义，故间接边界元法在理论和数值计算上都存在着缺陷。在直接法中，边界积分方程建立了待定函数在区域内的值与边界上的值之间的关系，具有直观的数学意义，并且一旦待定函数的边界值全部确定，其区域内的值也随之确定［2-3］，这样既减少了计算工作量，又便于结果的整理与分析。

通常，边界元法误差的主要来源是边界的离散误差和积分的计算误差［4］。在边界离散方面，单元的剖分是重要的一环。而在数值积分方面，误差主要包括数值积分的误差和奇异积分的处理，在奇异积分方面，许多学者已做了大量工作［5-7］。因此，找到一种快速且准确的边界离散形式和数值积分方法对进一步提高边界元法的计算精度将有很大的帮助。

本文将针对船舶水动力势流理论计算［8-9］，采用直接边界元法，先给出二维拉普拉斯方程边值问题的边界积分方程，然后分别采用常数单元、线性单元和二次单元对积分边界进行离散。在数值计算方面，将分别采用多种常用的数值积分方法对问题进行求解分析［10］，然后将所得数值解与解析解进行比较，着重讨论不同类型边界单元和不同数值积分方法对直接边界元法计算精度的影响，并选出一种适合于求解一般问题的边界离散形式和数值积分方法，进而推广至三维无限域问题，这对三维问题离散形式和积分方法的选取具有一定的指导意义。

1　数学模型

考虑在无限水深条件下无旋、非粘性、不可压缩来流中的任意物体，取一外部控制面将其封闭在内。流域的边界面由物面L组成，在边界上存在扰动速度势φ，在整个流场中满足流体质量守恒定理的二维拉普拉斯方程：

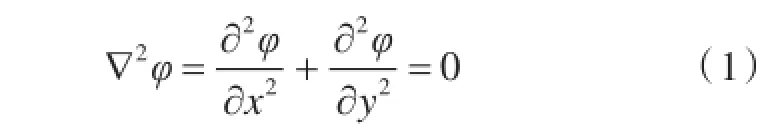
对于二维圆柱无界绕流，如图1所示，计算边界仅为物体表面LQ，需满足物面边界条件：

式中：φ为场点Q的待定函数，即φ(Q)；q¯为边界LQ上势函数u的法向导数的已知值；V∞为无穷远处均匀来流速度；nQ为边界上的单位内法向量。

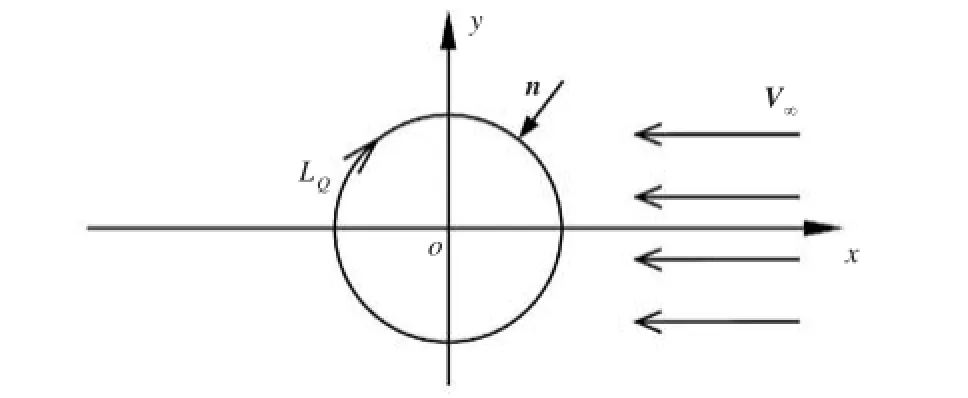
图1　二维圆柱绕流示意图Fig.1 Two dimensional flow around cylinder

二维圆柱无界绕流场中任意位置的速度势函数的解析解为

根据基本解的定义，二维拉普拉斯方程的基本解u*应满足

对于二维圆柱绕流，当场点P位于边界面上时，由物面条件和格林定理，可得场点P的速度势为

式中，r为源点Q与场点P之间的距离。

2　边界单元的划分

在边界离散方面，针对不同的具体问题，对边界量可以采用不同类型的插值函数，例如零次插值函数、线性插值函数和二次插值函数等，其相应的边界单元称为常数单元、线性单元和二次单元。

2.1常数单元

对于常数单元，如图2所示，节点取在边界单元的中点，边界上的函数值u和函数的法向导数值q在边界单元上为常量，并等于节点处的值。

图2　常数单元节点示意图Fig.2 Nodes of constantelement

在每个单元上对边界积分方程进行离散，可得

式中：uj和qj分别为边界单元节点处的函数值和函数的法向导数值；hij和gij分别为系数矩阵H 和G中的元素，其表达式为：当i=j时，

式中：li为边界单元的长度；dij为节点Pi到边界单元Li的垂直距离；rij为节点到积分单元上点的距离。从节点P1开始，依次对所有节点的hij和gij进行求解，利用Matlab对公式进行编程并计算出结果。

2.2线性单元

对于线性单元，如图3所示，节点取在边界单元的两端，边界上的函数值u和函数的法向导数值q在边界单元上服从线性分布，其离散化的边界积分方程为

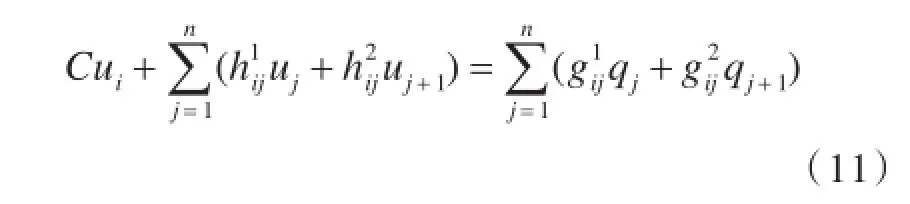
式中，uj，uj+1，qj，qj+1分别为边界单元上2个端点处的函数值和函数的法向导数值。

图3　线性单元节点示意图Fig.3Nodesoflinearelement

每个线性单元可用无因次坐标ξ表示为

式中，(x1，y1)，(x2，y2)分别为线性单元上起点与终点的坐标值。

将边界积分方程无因次化后可得hij和gij的表达式分别为：

式中：(xp，yp)为节点Pi的空间坐标；为雅克比行列式，对于二维线性单元，有J=lj。从节点P1开始，依次对各个节点的hij和gij进行求解，求解过程与常数单元相同。

当i=j时，边界积分方程的形函数C由下式确定：

由于系数C只与节点Pi处边界的几何形状有关，故两线性单元间的夹角为非定值，如图4所示。又因对角线元素Hii的计算包含有系数C和Cauchy型积分的计算，因此，采用一种简便的均匀场的办法便可间接计算C值。

图4　线性单元节点处夹角示意图Fig.4Anglearoundnodeoflinearelement

当一个均匀位势场作用于整个边界时，函数的法向导数值必定为零。因此，系数矩阵H的任意一行中所有元素的总和均为零，即

对于无限域问题，可设想所有内部边界被一个无限大的圆LR所包围，则除了出现在边界积分方程中的所有内部边界的积分外，还要加上在此大圆上的积分。

令R→∞，因

对边界积分方程离散化后，可得

而Gii可推导出其积分的解析表达式为

2.3二次单元

对于二次单元，如图5所示，节点分别取在边界单元的两端和中点，边界上的u和q在边界单元上服从二次分布。

图5　二次单元节点示意图Fig.5 Nodes of quadratic element

离散化后的边界积分方程为

式中：uj，uj+1，uj+2分别为边界单元上3个节点处的函数值；qj，qj+1，qj+2为其节点处函数的法向导数值。

每个二次单元可用无因次坐标ξ表示为

式中，(x1，y1)，(x2，y2)和(x3，y3)分别表示二次单元上3个节点的坐标值。

用二次单元离散后的边界积分方程的求解步骤与前2种单元均相同，只是边界单元中的积分函数有所不同，将边界积分方程无因次化后，可得hij和gij的表达式分别为：

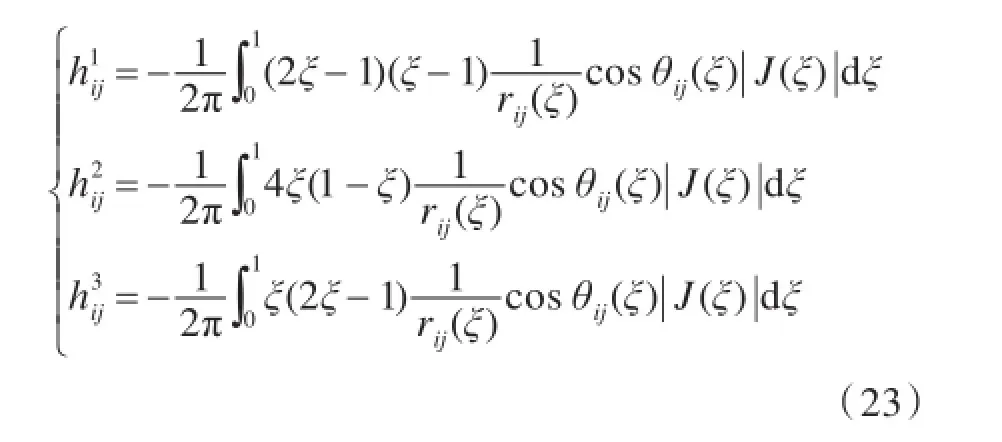
当i=j时，与线性单元相同，Hii可由式（17）和式（19）求得。而Gii由于公式过于复杂，无法推导出解析解表达式，而且在单元端点处的积分存在奇异性，所以只能采取积分上的近似解法，即取一趋近于0的极小值ε。在对g1ii和gi3i积分时，积分区间取为[1-ε，1+ε]；对gi2i积分时，积分区间取为[0，0.5-ε]和[0.5+ε，1]，按上述区间对gii的积分项进行积分，即可得到近似解。

值得说明的是，由于高斯积分法所取的高斯积分点一般在积分区间内，所以在积分过程中不需要求出带奇异性的端点值，在不改变积分区间的前提下可直接避开对积分奇异性的处理，并且多点高斯积分在计算精度方面也能满足一定的要求。所以，高斯积分法在处理二次单元的问题上存在着天然优势，该问题在后文中将予以详细讨论。

3　圆柱绕流算例及其精度分析

3.1数值积分方法与计算精度

用前文介绍的边界单元离散形式和数值积分方法对二维圆柱无界绕流问题进行求解。采用不同的节点数和数值积分方法对每种单元进行计算，边界单元离散的节点数依次从8取至200。之后，对每个节点处的计算值与解析值进行比较，求出相对误差并统计每次计算的时间，其结果如图6～图8所示。

由常数单元的计算结果可知，大部分数值积分方法从低节点数开始就能获得较高的精度，且随着节点数的增加，计算精度不断提高，但相应的计算时间也呈几何增长。其中，5点高斯积分公式法、龙贝格积分法等在精度和耗时方面都能获得比较满意的结果。在节点数为200时，其平均误差均能达到10-3～10-5量级的精度，可以满足工程应用需要。

图6　采用常数单元时各种积分方法的相对误差和计算时间Fig.6 Relative errors and calculation time of various integralmethodswhen using constantelement

图7　采用线性单元时各种积分方法的相对误差和计算时间Fig.7 Relative errors and calculation time of various integralmethodswhen using linear element

图8　采用二次单元时各种积分方法的相对误差和计算时间Fig.8 Relative errors and calculation time ofvarious integralmethodswhen using quadratic element

对于线性单元和二次单元，一部分数值积分方法已不适用于边界积分方程的求解，有的计算结果会出现较大的波动和偏差，有的甚至会发散。尤其是在二次单元时，例如，逐次半分区间梯形公式法等已经无法保证计算精度，平均误差达到了5%以上，且计算时间也呈指数增长，已超出边界元法可接受的范围。

综上所述，本文认为龙贝格积分法比较适合边界元法边界积分方程的求解，其在计算精度和计算时间上均能获得比较理想的结果。

3.2边界单元离散形式与计算精度

边界元法误差的另一个重要来源是边界的离散，单元的选择和划分对于计算结果的精度有着很大的影响，甚至超过了积分方法对精度的影响。在边界离散方面，一般公认的观点是边界单元数划分越多则计算精度越高，但边界单元的离散形式对精度的影响并没有一个定性的认识。本节将继续采用二维势流问题的计算结果，对使用相同数值积分方法不同离散形式下的计算精度和计算时间进行比较，比较结果如图9所示。

图9　不同离散方式下的相对误差和计算时间比较Fig.9 Relative errors and calculation time of various boundary discretizations

由计算结果可知，在3种边界单元离散形式中，常数单元的计算误差一般都要小于其余2种，且随着节点数的增多，常数单元的精度优势也更加明显。当划分的节点数达到200时，常数单元的误差基本上要比另2种单元的小一个数量级。此外，常数单元在计算时间上也远远优于其他单元，所耗时间通常只是其他单元的5%～10%。

从解析的角度分析，常数单元之所以优于线性单元和二次单元，很大一部分原因在于其对边界函数的近似程度。常数单元虽然将单元上的函数值设为了定值，但在网格足够多的前提下，常数单元反而能更好地表达离散物体表面的变化趋势。而线性单元和二次单元只是直接把单元上的函数值规定为按线性或二次变化，并不一定能完全反映函数实际的变化趋势。且线性单元和二次单元在具体的计算中会受到数值计算方法的限制，在含奇异积分的计算中无法推导出解析解，只能采用逼近奇点的近似解法。综合考虑单元数和离散形式，常数单元可以得出更准确的计算结果。

因此，本文认为在网格单元划分足够多的情况下，常数单元可以取代线性单元和二次单元对边界进行离散，并且计算误差和计算时间均可以满足边界元法在工程实际中的应用。

4　结语

边界元法由于采用了解析基本解，在计算精度上有限元法等数值方法难以与其相比。但许多学者由于对边界元法的误差来源了解不深，往往习惯性地采用高次单元，单纯地认为离散单元阶次越高，越能符合边界条件的变化，但这样反而不能把边界元法在计算精度和速度上的优势充分发挥出来。

本文首先通过算例证明了边界元法的主要误差是边界离散误差和数值积分误差，可见，正确地选择边界单元离散形式和数值积分方法是保证边界元法计算精度的第一要务。随后，验证了不同数值积分方法在求解边界积分方程中的适用性，通过与常用的高斯积分法进行对比，最终选出了一种精度较高、速度较快的积分方法——龙贝格积分法作为后续计算采用的方法。最后，通过对3种边界离散形式计算精度的分析，认为在网格单元划分足够多的情况下，常数单元可以取代线性单元和二次单元作为一般二维边界元问题的边界离散形式。从理论上说，该结论也可以推广到三维问题中，即常数单元在三维边界元问题中也能获得最佳的精度，但该推论的正确性还有待后续的研究验证。

［1］陈材侃.计算流体力学［M］.重庆：重庆出版社，1992.

［2］BREBBIA C A.The boundary element method for engineers［M］.London：Pentech Press，1978.

［3］BREBBIA C A，TELLES JC F，WROBEL L.Boundary element techniques：theory and applications in engineering［M］.Berlin：Springer-Verlag，1984.

［4］姚振汉，王海涛.边界元法［M］.北京：高等教育出版社，2010.

［5］KLASEBOER E，FERNANDEZ C R，KHOO B C.A note on true desingularisation of boundary integral methods for three-dimensional potential problems［J］. Engineering Analysis With Boundary Elements，2009，33（6）：796-801.

［6］周焕林，牛忠荣，程长征，等.各向异性位势问题边界元法中几乎奇异积分的解析算法［J］.计算力学学报，2008，25（3）：333-338. ZHOU Huanlin，NIU Zhongrong，CHENG Changzheng，et al.Analytical algorithm of the nearly singular integrals in boundary elementmethod to anisotropic potential problems［J］.Chinese Journal of Computational Mechanics，2008，25（3）：333-338.

［7］马荣，刘继朝，石建省.边界元法中角点问题的一种计算方法［J］.中国科学院研究生院学报，2011，28 （3）：315-321. MA Rong，LIU Jichao，SHI Jiansheng.A new algorithm to solve corner problem in the boundary element method［J］.Journal of the Graduate School of the Chinese Academy of Sciences，2011，28（3）：315-321.

［8］MIAO Q M，CHWANG A T.Ship waves by direct boundary elementmethod［J］.Journal of Ship Mechanics，2003，7（6）：27-36.

［9］BELIBASSAKISK A，GEROSTATHIS T P，KOSTAS K V，et al.A BEM-isogeometric method for the ship wave-resistanceproblem［J］.Ocean Engineering，2013，60（1）：53-67.

［10］MATHEWS JH，FINK K D.Numericalmethods using Matlab［M］.NJ：Prentice Hall，2004.

［责任编辑：卢圣芳］

Precision analysis of the two-dimensional potential flow problem in an in finite region with the direct boundary element method

HAN Yuchao，LU Xiaoping，WANGZhong Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

The Boundary Element Method（BEM），as a key numerical method，has been widely applied in many fields.However，the research on the Direct Boundary Element Method（DBEM）for ship hydrodynamic numerical calculation problems is still insufficient，especially when it comes to the ship hydrodynamic potential flow theory.The general method-‘panel method'-is based on Hess-Smith method，which is an Indirect Boundary ElementMethod（IBEM）whosemajor flaws exist in both theory and numerical calculation.This paper，based on the ship hydrodynamic potential flow theory，adopts DBEM to calculate the example of two-dimensional unbounded potential flow around a cylinder，and analyzes the influence of the boundary element discrete forms and the numerical integralmethods on the calculation accuracy.The results carried out by Matlab clearly indicate that using the constant element and Romberg algorithm method could yield high calculation speed and accuracy.

Direct Boundary Element Method（DBEM）；potential flow theory；boundary discretization；numerical integration

U661.1

A

10.3969/j.issn.1673-3185.2015.04.006

2014-09-04网络出版时间：2015-7-28 17:25:18

国家部委基金资助项目

韩玉超，男，1989年生，硕士生。研究方向：舰船水动力性能。E-mail：hanyuchaoa@163.com卢晓平（通信作者），男，1957年生，博士，教授。研究方向：舰船水动力性能。E-mail：Luxiaoping100@163.com王中，男，1981年生，博士，讲师。研究方向：计算机辅助船舶设计制造。E-mail：wangzhonghj@sohu.com