基坑支护入土深度上限解研究

李和志，赵 鹿，郭 丽

（江西科技学院 土木工程学院，江西 南昌 330098）

基坑支护入土深度上限解研究

李和志，赵 鹿，郭 丽

（江西科技学院 土木工程学院，江西 南昌 330098）

基于极限分析上限法分析了基坑底部刚塑性三角形楔体和对数螺旋线三个受剪区的速度场，建立了基坑底部塑性区的虚功率方程，据此推导出基坑抗隆起稳定安全性要求下的支护入土深度上限解和支护入土深度一定时的基坑抗隆起稳定性安全系数，且经工程实例验证可知，基坑支护入土深度上限解和抗隆起稳定性安全系数计算式是可以接受的。

极限分析；上限解；基坑；支护深度

随着城市化快速发展，一些城市人口剧增，从而引起建筑用地变得相当紧张，进而促使了基坑工程发展，然而由于基坑工程周边环境和地质情况复杂性，基坑安全事故不断发生，所造成的损失触目惊心，为减少基坑安全事故的发生和保障施工人员及周边民众的安全，必须对基坑稳定性进行细致深入的研究，可喜的是，已有众多的理论研究者对基坑稳定性进行了较为全面的研究，并取得了骄人研究成果[1-8]。由于基坑稳定性全面性分析是极其复杂的，它包括：整体稳定性分析、基坑坑底土体抗隆起稳定分析、支护桩抗倾覆稳定性分析、基坑渗流稳定性分析等等，但具体对于不同的土质条件，基坑稳定性侧重有所不同。近年来在软土基坑支护实践表明，基坑底部土体抗隆起稳定性往往起到安全决定作用，而在抗隆起稳定性分析时，除了对基坑底部土体处置外，通常采用的是调整支护桩的入土深度来达到基坑底部土体稳定的目的，正是基于此，下面将通过极限分析上限法来确定软土基坑支护入土深度值。

1 软土基坑支护坑底速度场分析

软土基坑坑底土体在其一侧土体自重及外荷载作用下达到极限状态时，就会发生塑性流动，而它的流动方向迹线就是速度滑移线。假定忽略AE面摩擦力和假设滑移场土体为Coulomb材料且忽略其自重，基坑承受外荷载为q0，基坑开挖深度为H，土体为均质土且其重度为γ，粘聚力为c,内摩擦角为φ，基坑支护入土深度为t，则基坑支护桩底面以下的坑底土体主动区ABC所受的荷载值为q=q0+γ(t+H)，被动区BDE所承受的荷载值为q1=γt，于是，可建立如图1所示的坑底滑移场和基于Hill机构建立如图2所示的基坑坑底塑性区速度场，类似于文献9图3.22（a）Hill机构分析可知，该速度场由底角为的主动滑移区ABC、中心角为的BCD对数螺旋过渡区及底角为的被动滑移区BDE构成。

图1 基坑底部滑移线场

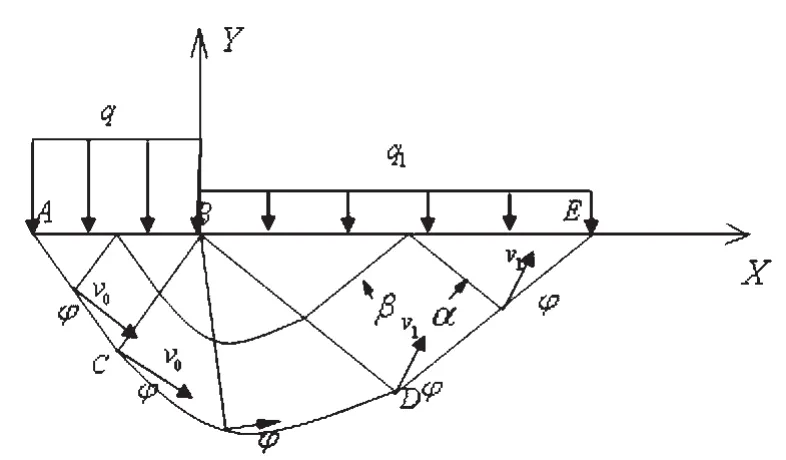
图2 基于Hill机构的速度场

因为塑性流动线ACDE以下的土体不受塑性变形影响，可视为静止状态，故此流动线为一条速度间断线，根据速度间断线特点可知道，此线上的任何一点的速度方向与该点切线成φ角，即ACDEBA整个区域的ACDE边界上速度方向与该线成φ角，显然速度方向垂直塑性区一侧的α族滑移线，故而塑性区一侧的α族滑移线的速度vα=0，又在ACDEBA整个区域中α族滑移线均为直线，则此整个区域内的速度vα均为零，同时在刚性区一侧的速度突变为零[9]。

1.1 主动滑移区ABC区域速度场分析

因AC边界上速度方向与该线成φ角，故而此区域在AB以上的压力q作用下产生以速度vo作垂直于BC面的塑性运动，假定支护桩底面以上的速度为v，则根据AB面的速度相容条件可知：

1.2 过渡区BCD区域速度场分析

在此区域中已知，vα=0，则根据沿β族滑移线速度场基本微分方程有[10]：

式中K为积分常数，根据边界条件求出。

不难分析，间断线BC右侧的速度及大小与其左侧完全一致：

同时对数螺旋区边界BC右侧的vβ为：

而边界BC右侧的vβ还可由式 (3.23)表示，且

于是可求的积分常数K为：

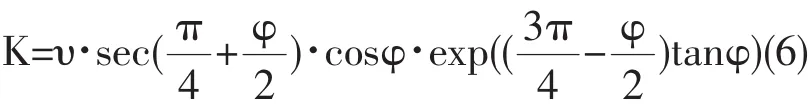
因而，对数螺旋过渡区BCD中沿α族、β族滑移线的速度为：

进而对数螺旋过渡区BCD中的速度为：

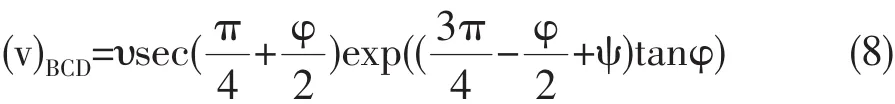
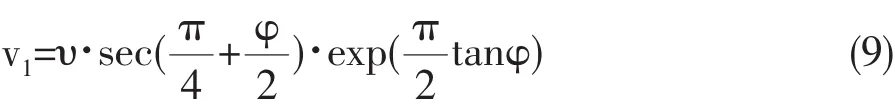
因而可知对数螺旋过渡区BCD的速度按指数规律由边线BC的(v右)BC逐渐变为BD的v1。

1.3被动滑移区BDE区域速度场分析

因被动区BDE的边界BD的滑移速度方向与边界DE成φ角，不难证明边界BD的滑移速度方向与边界BD垂直，且其大小因在边界BD两侧的速度方向未发生改变而不变，即依旧为v1，并且此区域与主动区ABC有相似的特性，即都是均匀速度区，则被动区BDE可看成以速度v1垂直于BD面斜向上的刚体运动。

2 软土基坑支护入土深度上限解

经速度场分析可知，主动区ABC以速度vo与 x轴正向成－()夹角作刚体运动，被动区BDE以速度v1与 x轴正向成()的夹角作刚体运动，对数螺旋过渡区BCD以速度 (v)BCD绕B点按对数螺旋运动，ACDE间断面因其以下土体未发生运动，故而是一个速度间断面，BC、BD两面经上文分析可知并非跟Prandtl机构场一样，而是一个速度连续面，主动区ABC所受的荷载值为q以速度v且方向垂直向下，被动区BDE所受的荷载值为q1以速度v2=v1cos()且方向垂直向上。

为一般性研究基坑支护后坑底土体极限承载能力，先暂时假设速度间断面AB长为b，则根据图2及相关分析可知道：

此外，还可根据对数螺旋区BCD中的BC与BD的长度关系可推出：

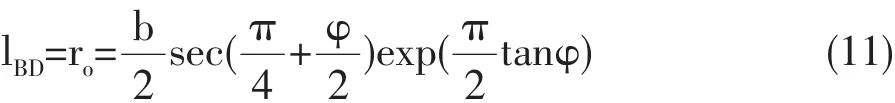
再根据图2及相关分析可得到：

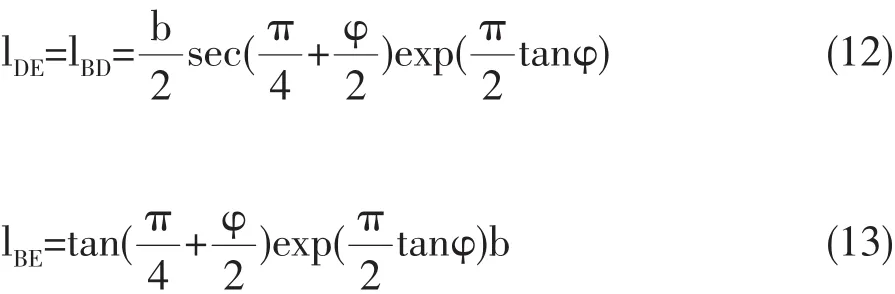
经上述分析可知，忽略滑动区内土体自重，则此机构场中q做正功，q1做负功，间断面AC、CD、DE及对数螺旋区BCD均存有能量耗散。其中间断面AC、DE属于平移情况下的能量消散，可分别通过以下两式求出：

隔离过渡区BCD区域，并建立如图3所示的极坐标分析图，故而在计算间断面CD能量消散CD时，还需要将其速度通过换元公式换成与矢径r相关的θ的参数，即假设ψ=θ－π，则式(8)可化为：

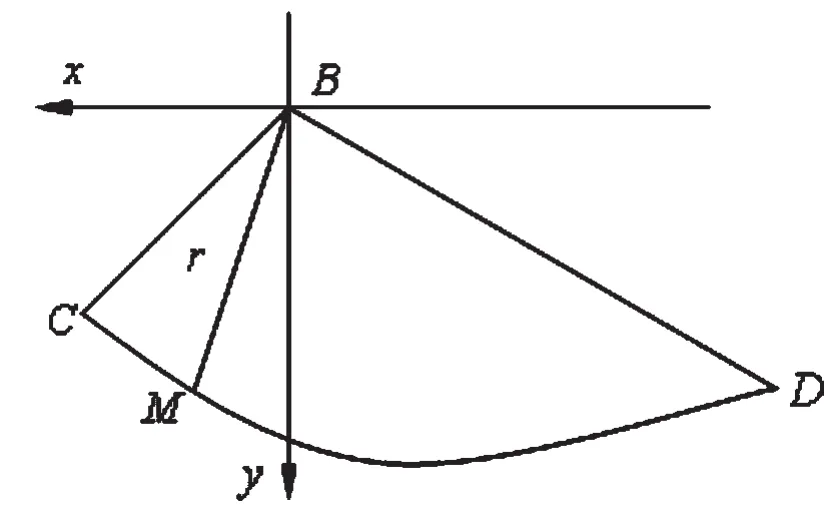
图3BCD区域极坐标分析简图

至此，则可通过对c·(v)BCD·cosφ微元积分求出对数螺旋区BCD速度间断线CD上的能量消散率CD:

图4 对数螺旋区BCD能量消散率计算简图

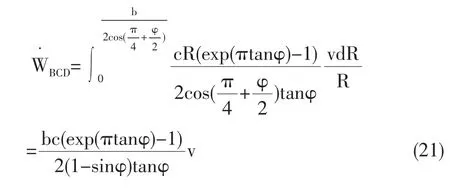
外荷载q1对此机构产生负功率q1为：·

忽略此机构场土体的自重，再结合式 (14)、式(15)、式(18)、式(21)、式(22)、式(23)，可建立虚功率方程：

对此虚功率方程求解，便可求得基坑支护入土深度的上限解和基坑底部极限荷载：

此外，假设实际支护入土深度为t，则基坑抗隆起稳定性安全系数k：

3 工程算例

采用文献1中工程实例作为算例，该主楼基坑开挖深度H为11.65m，支护桩桩长l为24.55m，超载q0取值20kPa。，基坑围护设计参数见表1。

根据式（25）和该基坑的围护设计参数，并假设支护桩桩底在土层4内，可计算出该基坑的抗隆起稳定性理论支护入土深度上限解为4.05m，超过3.7m,但是考虑到5-1a土层的参数与土层4接近，且为安全考虑，该主楼支护桩入土深度上限解就是4.05m。此外该基坑实际支护入土深度为12.9m，且坑底土层参数取土层4、5-1a、5-1b的厚度加权值，运用式（27），可以求得该抗隆起稳定性安全系数k为1.94，且与文献1中表2对比可知，本文稳定性分析是合理的，也从侧面上验证了本文基坑支护入土深度上限解。

表1 基坑围护设计参数

4 结语

本文基于极限分析上限法分析了基坑底部主动滑移区、过渡区域和被动滑移区的速度场，建立相应的虚功率方程，推导了基坑抗隆起稳定安全性要求下的支护深度上限解和支护入土深度一定时的基坑抗隆起稳定性安全系数。

[1]秦会来，陈祖煜，刘立鹏.基于上限理论的软土基坑抗隆起稳定分析方法[J].岩土工程学报，2012,34(9).

[2]陈刚，阮澍，李九思.软土基坑喷锚支护设计与实例分析[J].岩土力学，2002,23（S1）.

[3]秦会来，黄茂松，王卫东.非均质软土基坑抗隆起稳定性的极限分析方法[J].岩土力学，2008,29(10).

[4]张耀东，龚晓南.软土基坑抗隆起稳定性计算的改进[J].岩土工程学报，2006,28(S1).

[5]李镜培，唐耀，张飞.考虑支护结构的软土基坑抗隆起稳定上限分析[J].地下空间与工程学报，2011,17(5).

[6]SHIRAW J，WEN D，NADARAJAH P，et al.Design issues related to jet grouted piles at base of excavations[C].Proc Tunnels and Underground Strutctures，Singapore Aa Balkema，2000：639-645.

[7]张玉成，杨光华，钟志辉等.软土基坑设计若干关键问题探讨及基坑设计实例应用分析 [J].岩石力学与工程学报，2012,31(11).

[8]刘润,闫玥,闫澍旺.支撑位置对基坑整体稳定性的影响[J].岩石力学与工程学报,2006(1).

[9]龚晓南.土塑性力学[M].杭州：浙江大学出版社，1997.

（责任编辑：陈 辉）

Research for Upper-bound Solution to the Depth of the Driven Excavations

LI He-zhi，ZHAO lu，GUO li
（School of Civil Engineering,Jiangxi University of Technology,Nanchang 330098,China）

Based on upper bound theorem of the limit analysis method,the paper analyzes the velocity field at the bottom of active slip zone ABC and transition zone BCD and passive slip zone BDE,and sets up virtual work-rate equation,reckons upper-bound solution to excavations supporting depth which satisfies the foundation heave stable security requirement.Besides,foundation heave stability safety factor is solved.Cited with engineering examples,upperbound solution of supporting depth excavation and foundation heave stability safety factor are proved to be accepted.

limit analysis;upper-bound solution;excavations;supporting depth

TU443

A

123(2015)01-0022-05

2014-03-20

李和志(1985-)，男，湖南双峰人，江西科技学院土木工程学院，讲师，工程师，硕士。研究方向：边坡工程及地基基础研究与教学。

2014年江西科技学院自然科学研究项目"软岩隧道底鼓机理及防治技术研究"（NO.ZR14YB08）。