单项式多变量公钥密码算法的等价密钥问题

魏占祯，袁峰，许盛伟，江继军

(1.北京电子科技学院通信工程系，北京100070;2.北京电子科技学院信息安全研究所，北京100070)

1994 年，Peter Shor［1］提出了多项式时间内的量子大整数分解算法。这意味着一旦造出实用的量子计算机后，基于大整数分解和离散对数问题的传统公钥密码算法将会是不安全的。基于有限域上多元多项式方程组的多变量公钥密码算法被认为是能抵抗量子计算机攻击的几种公钥密码算法之一，其安全性基础是解有限域上的多元多项式方程组，而这一问题是NP-困难问题［1］。较之于传统公钥密码算法［2］，多变量公钥密码算法具有速度快、易于实现等优点［3-5］。多变量公钥密码算法中存在着多个私钥对应于同一个公钥的等价密钥问题。Wolf等在文献［6］中分别研究了C*，C*-和 HFE 等［1，7］著名算法的等价密钥问题，计算出了这些算法的等价密钥数量。并且，Wolf等指出，任一公钥都有指数级个私钥与之对应，从而使私钥空间大量减少。通过应用保形变换，将私钥的线性部分化为具有稀疏特性的矩阵，选该形式作为等价类的代表元，可以有效地减少运算量，从而有助于存储的高效实现。同时，等价密钥的存在导致实际安全参数空间的规模也大为减少，要想达到预想的安全强度就必须提高算法参数的大小［6］。多变量公钥密码算法C*，C*-和Square等［1，8］是中心映射为一般单项式的多变量公钥密码算法［9］的特例，即中心映射为一般单项式的多变量公钥密码算法是以上这些著名算法更为一般的推广形式，若能计算出其等价密钥的数量，就可直接推出这些“特例”算法等价密钥的数量。本文对中心映射为一般单项式的多变量公钥密码算法的等价密钥问题进行了研究，利用保形变换和有限域方面的知识计算出了其等价密钥的具体数量。

1 等价密钥和保形变换

本节介绍多变量公钥密码中等价密钥和保形变换的定义，以及有限域上的一些结论。

设k是q阶元素的有限域，即k=GF(q)。若g(x)是域k上的n次不可约多项式，则K=k［x］/(g(x))是域k的n次扩域，即K=GF(qn)。设φ:K→kn是域K到域k上n维线性空间的同构映射，即 φ(a0+a1α+…+an-1αn-1)=(a0，a1，…，an-1)。

多变量公钥密码算法的关键思想［1］是用2个可逆线性仿射(或可逆线性映射)U:kn→kn和T:kn→kn来隐藏中心映射F'。若F'是从kn到kn的映射，令F=F'，则合成映射P:kn→kn是:

若F'是从域K到域K的映射，令F=φ◦F'◦φ-1，即F是从kn到kn的映射，则合成映射P:kn→kn是:

定义 1［6］若 2 组密钥 (T，F，U)和能够使得

则称这2组密钥是等价的。

事实上，多变量公钥密码的等价密钥问题就是指对应公钥相同，对私钥空间划分等价类。

定义 2［6］映射ρ:kn→kn和 ω:kn→kn是2个可逆线性仿射，可知:

若ρ和ω能够使得映射F的形状保持不变，即映射F与ω◦F◦ρ在表达形式上是相同的，则称ρ和ω为保形变换。

事实上，所定义的保形变换ρ和ω必须要使映射F的形状保持不变，在这种情况下，所得到的映射ρ-1◦U和T◦ω-1的数量，就是等价密钥的数量。

通过应用保形变换ρ和ω，将可逆线性仿射U和T所对应的矩阵化为具有“稀疏”特性的标准形式。在计算资源和存储空间都受限的场合，如智能卡、传感器平台、无线射频识别上，选具有“稀疏”特性的标准形作为等价类的代表元，可以有效地减少计算量，提高存储效率。

引理 1［10］

其中，GLn(Fq)为域Fq上的可逆矩阵群。

引理1给出了域Fq上n×n阶可逆矩阵的数量。

引理2［1］若多项式映射L:K→K是:

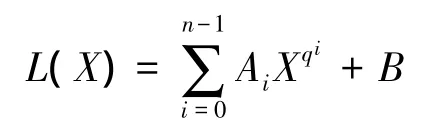
其中，Ai，B∈K。令，则是一个多项式映射:

引理2揭示了域K上的线性化多项式:

与kn上线性仿射y=Cx+D之间存在着一一对应关系，其中C∈kn×n，D∈kn，x=(x0，x1，…，xn-1)∈kn，y=(y0，y1，…，yn-1)∈kn。

下面的引理3是引理2的推广，引理3揭示了kn上的二次多项式与扩域K上的多项式映射之间的一一对应关系。

引理3［1］若多项式映射F:K→K是:

2 单项式多变量公钥密码算法的等价密钥数量

本节讨论中心映射为一般单项式F'(X)=(t＜q)的多变量公钥密码算法的等价密钥问题。下面的定理1讨论了l1，l2，…，lt∈{0，1，2，…，n-1}且l1，l2，…，lt全不相同时的情形;定理2 讨论了l1，l2，…，lt∈{0，1，2，…，n-1}且l1=l2=…=lt-1=lt时的情形。这2个结果非常一般，由这2个结果可直接推出一些基于单项式的多变量公钥算法等价密钥的数量，如C*算法和Square算法。

定理1 对于域K=GF(qn)上的中心映射F'(X)=Xql1+ql2+…+qlt，t＜q，l1，l2，…，lt∈ {0，1，2，…，n-1}且l1，l2，…，lt全不相同，使得F=ω◦F◦ρ成立的可逆线性仿射ρ和ω的数量为n(qn-1)，其中ρ和 ω的线性化多项式形式为 ρ(X)=AXqc和ω(X)=A-qn-c(qi1+qi2+…+qit)Xqn-c，c=0，1，…，n-1，0 ≠A∈K。

证明:由F=ω◦F◦ρ可得ω-1◦F=F◦ρ。根据引理2，可设

由于t＜q，则可推出ql1+ql2+…+qlt≤qn-1+qn-1+ … +qn-1=tqn-1＜qn;由于l1，l2，…，lt∈{0，1，2，…，n-1}且l1，l2，…，lt全不相同，则l1+i，l2+i，…，lt+i也全不相同。因此，对比等式F◦ρ(X)=ω-1◦F(X)两边各项系数可以发现，等式左边形如Xqa+qa+…+qa的单项式的系数为0，这里qa+qa+…+qa共有t项，a=0，1，…，n-1，即有如下n个方程:

这里i1，i2，…，it∈{0，1，2，…，n-1}，且i1，i2，…，it全不相同。要想使以上n个方程成立，就要求在A10，A11，…，A1n-1中至少有 2 个值为 0，不妨设A1n-2=0，A1n-1=0。进一步可以发现，存在形如Xqa+qa+…+qa+qb的单项式的系数为0，这里qa+qa+…+qa+qb共有t项，a∈{0，1，…，n-1}，b=0，1，…，n-1，即有如下形式的方程:

这里j1，j2，…，jt∈ {0，1，2，…，n-1}。要想使以上方程成立，就要求在A10，A11，…，A1n-3中至少有一个值为0，不妨设A1n-3=0。进一步还可以发现，存在形如Xqa+qa+…+qa+qb+qb的单项式的系数为0，其中qa+qa+…+qa+qb+qb总共有t项，a∈{0，1，…，n-1}，b=0，1，…，n-1，即有如下形式的方程:

这里k1，k2，…，kt∈ {0，1，2，…，n-1}。要想使以上方程成立，就要求在A10，A11，…，A1n-4中至少有一个值为0，不妨设A1n-4=0。以此类推，能够发现，有且仅有一个A1m≠ 0，0≤m≤n-1，其余A1i=0，i≠m。因而就有

形如Xqi1+qi2+…+qit-1的单项式的系数为0，其中qi1+qi2+…+qit-1共有t-1 项，i1，i2，…，it-1∈ {0，1，2，…，n-1}，且i1，i2，…，it-1全不相同，即有如下形式的方程:

要想使以上方程成立，就要求D=0。由于G=Dqi1+qi2+…+qit，因此G=0。再对比等式F◦ρ(X)=ω-1◦F(X)两边各项系数能够得到，C2m≠0，0≤m≤n-1，C2i=0，i≠m。

根据以上分析可设，

其中，0≤c，d≤n-1，A，C∈K。由于映射ω与ω-1互逆，因此ω(X)=C-qn-dXqn-d。再根据等式ω◦F◦ρ(X)=F(X)可得

即C-qn-dAqn-d(qi1+qi2+…+qit)=1，c=d，则可逆线性仿射 ρ和ω的线性化多项式形式就是 ρ(X)=AXqc和ω(X)=A-qn-c(qi1+qi2+…+qit)Xqn-c，c=0，1，…，n-1，A∈K，因而具有这样形式的可逆线性仿射ρ和ω的数量即为n(qn-1)。

定理2 对于域K=GF(qn)上的中心映射F'(X)=Xql1+ql2+…+qlt，t＜q，l1，l2，…，lt∈ {0，1，2，…，n-1}且l1=l2=…=lt-1=lt，使得F=ω◦F◦ρ成立的可逆线性仿射ρ和ω的数量为n(qn-1)，其中ρ和 ω的线性化多项式形式为 ρ(X)=AXqc和ω(X)=A-qn-c(qi1+qi2+…+qit)Xqn-c，c=0，1，…，n-1，0 ≠A∈K。

证明:由F=ω◦F◦ρ可得ω-1◦F=F◦ρ。根据引理2，可设

其中，A1i，B2i，C2i，D，S，G∈K=GF(qn)。

由等式ω-1◦F(X)=F◦ρ(X)可知，对比常数项可得

对比n个单项式Xq0，Xq1，…，Xqn-1的系数，可得以下n个等式:

对比以下n(n-1)个单项式:

设域k=GF(q)的特征为素数p，q=pm，m≥1，则有以下2种情形:

情形1 若 (p，t)=1，由式(2)可知，D=0或A1i=0，0≤i≤n-1。根据映射ρ是可逆线性仿射，A1i(0≤i≤n-1)都为0是不可能的，因此，由式(2)可推出D=0。再由式(1)可得，G=0。

由式(3)可推出，在A10，A11，…，A1n-1中至少有n-1个值为0，再根据映射ρ是可逆线性仿射可得，有且仅有一个A1c=A≠0，0≤c≤n-1，其余A1i=0，i≠c。以下证明过程与定理1的证明过程相同。

情形2 若p|t，可设t=pew，(p，w)=1，e，w≥1 ，则tql1=wpml1+e，就有

由于(p，w)=1，以下证明过程与情形1的证明过程相似。

3 C*算法和Square算法的等价密钥数量

在C*算法［1］中，域k是q阶元素且特征为2的有限域，域K是域k的n次扩域。中心映射F'是:F'(X)=Xqθ+1，X∈K，其中 θ要使qθ+1与qn-1互素，即gcd(qθ+1，qn-1)=1且0＜θ＜n。

由于C*算法的中心映射F'为F'(X)=Xqθ+q0，0＜θ＜n，q=2m(一般情况下m＞1，著名的SFLASH算法［1，9］的推荐参数为q=27)，因此，2=t＜q=2m，l1=0，l2=θ，l1，l2∈ {0，1，2，…，n-1}且l1≠l2，根据定理1，可得以下推论1。

推论1 若C*算法的私钥是(T，F，U)，则等价密钥的数量是n(qn-1)。

在Square算法［8］中，域k是q阶元素的有限域，其中q≡3 mod 4，域K是域k的n+l次扩域。中心映射F'是:F'(X)=X2，X∈K。映射T:kn+l→kn+l是可逆线性仿射，映射U-:kn→kn+l是将可逆线性仿射U:kn+l→kn+l(线性部分)的最后l列删掉。

由于Square算法的中心映射F'为F'(X)=Xq0+q0，q≡3 mod 4(q＞3，Square算法［8］的推荐参数为q=31)，因此，2=t＜q，l1=l2=0且l1，l2∈{0，1，2，…，n-1}，根据定理 2，可直接得到以下推论 2。

推论2 对于特征不为2的域K上的中心映射F'(X)=X2，使得F=ω◦F◦ρ成立的可逆线性仿射ρ和ω的数量为n(qn-1)，其中ρ和ω的线性化多项式形式为 ρ(X)=BXqt和 ω(X)=B-2qn-tXqn-t，t=0，…，n-1，0≠B∈K。

推论3 若Square算法的私钥为(T，F，U)，l是可逆线性仿射U删掉的列数，则等价密钥的数量是

证明:由于可逆线性仿射U和T的数量为(n+l)(qn+l-1)，U-是将线性仿射U的线性部分的最后l列删掉，因此，在U-端就产生了倍的等价密钥。注意到T和U-两端的变换是独立的，所以直接相乘就能得到结论。

4 结束语

等价密钥问题是多变量公钥密码算法中一类重要的问题，中心映射为一般单项式的多变量公钥密码算法是C*，C*-和Square等著名算法更为一般的推广形式。本文利用保形变换和一些数学技巧计算出了中心映射为一般单项式的多变量公钥密码算法等价密钥的数量。所得到的结果可直接推出C*，C*-和Square等著名算法等价密钥的数量。目前对于中心映射为高次多元多项式(如高次二项式)的等价密钥问题仍然没有结果，将来可尝试计算中心映射为一般多元多项式的多变量公钥密码算法等价密钥的数量。

［1］DING Jintai，GOWER J E，SCHMIDT D S.Multivariate public key cryptosystems［M］.New York:Springer，2006:2-3，246-247.

［2］刘振华，胡予濮，牟宁波.基于身份认证密钥协商的分析与改进［J］.哈尔滨工程大学学报，2009，30(10):1194-1198.LIU Zhenhua，HU Yupu，MU Ningbo.Analysis and improvement of identity-based authenticated key agreement［J］.Journal of Harbin Engineering University，2009，30(10):1194-1198.

［3］BETTALE L，FAUGÈRE J C，PERRET L.Cryptanalysis of HFE，multi-HFE and variants for odd and even characteristic［J］.Designs，Codes and Cryptography，2013，69(1):1-52.

［4］GAO Shuhong，HEINDL R.Multivariate public key cryptosystems from diophantine equations［J］.Designs，Codes and Cryptography，2013，67(1):1-18.

［5］YUAN Feng，SUN Ying，JIANG Jijun，et al.A multivariate public key cryptographic scheme［J］.China Communications，2014，11(12):120-124.

［6］WOLF C，PRENEEL B.Equivalent keys in HFE，C*，and variations［C］//Progress in Cryptology-MYCRPT 2005.Berlin，2005:33-49.

［7］BOUILLAGUET C，FOUQUE P A，VÉBER A.Graph-theoretic algorithms for the“isomorphism of polynomials”problem［C］//Advances in Cryptology-EUROCRYPT 2013.Berlin，2013:211-227.

［8］DING Jintai，CLOUGH C，ARAUJO R.Inverting square systems algebraically is exponential［J］.Finite Fields and Their Applications，2014，26:32-48.

［9］CAO Weiwei，HU Lei.Projective interpolation of polynomial vectors and improved key recovery attack on SFLASH［J］.Designs，Codes and Cryptography，2014，73(3):719-730.

［10］万哲先.有限域上典型群的几何学［M］.第2版.北京:科学出版社，2002:4-5.