直接边界元法解势流速度场问题

李井煜，卢晓平，赵鹏伟

直接边界元法解势流速度场问题

李井煜，卢晓平，赵鹏伟

海军工程大学舰船工程系，湖北武汉430033

在船舶水动力学中，大多采用以Hess-Smith方法为基础的间接边界元法求解势流绕流问题，但Hess-Smith方法本质上是基于物理直观提出，在理论和数值计算上都存在着缺点。直接边界元法虽然在船舶水动力领域有着非常广阔的应用前景，但至今应用较少。为推广直接边界元法在船舶水动力学中的应用，根据边界积分法建立积分方程，采用直接边界元法对无界势流绕流问题予以求解，得出流场速度势和物面上的速度分布，并通过与解析解的比较进行误差分析。对二维、三维问题的算例进行数值计算。数值计算过程用Matlab编程实现。结果表明：直接边界元法在求解船舶势流绕流问题中具有足够的精度和较高的效率，且数值计算实现过程更简洁，可发展成为求解船舶兴波等船舶水动力学问题的通用方法。

直接边界元法；势流理论；数值积分；船舶水动力学

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20150128.1201.005.html

期刊网址：www.ship-research.com

引用格式：李井煜，卢晓平，赵鹏伟.直接边界元法解势流速度场问题［J］.中国舰船研究，2015，10（1）：68-75. LI Jingyu，LU Xiaoping，ZHAO Pengwei.Direct boundary element method for the problem of potential flow velocity field［J］.Chinese Journal of Ship Research，2015，10（1）：68-75.

0　引言

船舶水动力学中的许多问题都可以归结为按初始条件和边界条件求解偏微分方程的初值和边值问题，但能求出解析解的仅限于极少数情况，故一般只用数值方法求出近似解。边界元法是一种很好的求解船舶水动力学问题的数值计算方法，经过几十年的发展，其已经在诸多领域得到广泛应用。相比有限元法等其他数值计算方法，边界元法的优势在于利用了“降维”功能，从而可以大大减少对计算机存储的需求［1-2］。采用边界元法仅需在计算域的边界上进行求解即可，其可将三维问题转化为二维问题，或者将二维问题转化为一维问题，且能方便处理无界区域问题，这也是边界元法在求解船舶水动力学势流绕流问题中得到广泛应用的重要原因之一。

边界元法分直接法和间接法2类。直接法是用物理意义明确的变量来建立积分方程，积分方程中的未知函数就是物理量在边界上的值；间接法是用物理意义不一定明确的变量来建立积分方程，例如源分布或偶极子分布函数的概念，都是基于物理直观提出，其在理论和数值计算上都存在着缺点，不便于在工程应用中推广。边界元法在船舶水动力问题上的应用可追溯到Hess-Smith方法。该方法是一种以源分布函数为未知函数的间接方法，或许是基于这个原因，后续在船舶兴波、耐波性和操纵性问题的势流理论求解中大多采用以Hess-Smith法为基础的间接法，长期以来，该方法在求解船舶水动力学势流问题中发挥着重要作用［3-5］。

针对船舶水动力学数值求解中的这种趋势，提出采用直接边界元法求解船舶水动力的势流绕流问题，直接将变量取为流场的速度势，然后求解流动区域或边界上的速度场，并采用简单的算例进行数值计算。通过比较数值解和解析解［6］，分析计算精度。对于二维流动，选取无限域的均匀来流为计算模型，对于三维流场，则选取无限域圆球绕流为计算模型。所做研究可为进一步推广使用直接边界元法求解带有兴波面、附体或多片体等复杂边界条件的船舶势流绕流问题打下基础。

1　二维势流问题算例

1.1数学模型

考虑无穷远边界的流场，有沿y轴正向的速度为1的均匀来流，流体为无旋、无粘性、不可压缩的理想流体。研究边长为1的正方形区域流场，定解问题如下：

根据第三格林公式，可得到相应的边界积分方程为

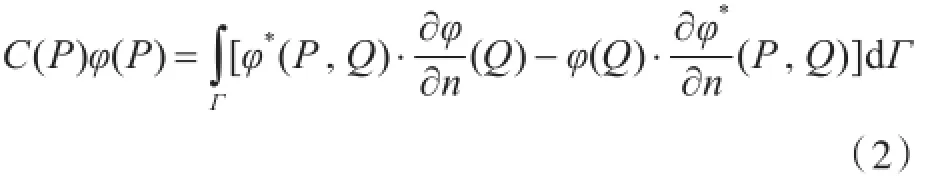
式中：Γ为边界线；φ为速度势；φ*为拉普拉斯算子的基本解（或称格林函数），在二维问题中

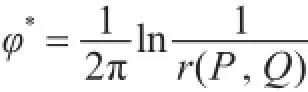
其中，r（P，Q）为场点P与源点Q之间的距离；C为

其中，θ在二维中为边界点P处边界切线的夹角，在三维中为边界点P的立体角。当边界Γ光滑时，C（P）=1/2。当场点P取在边界上时，式（2）即为求解边界上速度势φ的边界积分方程，根据边界上的速度势，可进一步解出流场中任意点的速度势。

1.2离散与数值求解

要采用直接边界元法求解式（1）所示的边界积分方程，需对边界划分单元。如图1所示，将正方形边界划分为20个单元，在每个单元上选取插值函数模式，将边界积分方程离散后，即转化为线性方程组，据此，便可对边界上的速度势φ进行求解。

图1　正方形网格区域Fig.1　A square flow field area

1.2.1常数单元

对于常数单元，单元节点位于单元中点处。如图2所示，将每个单元上的物理量等）都设为常量，且取为节点上的值。

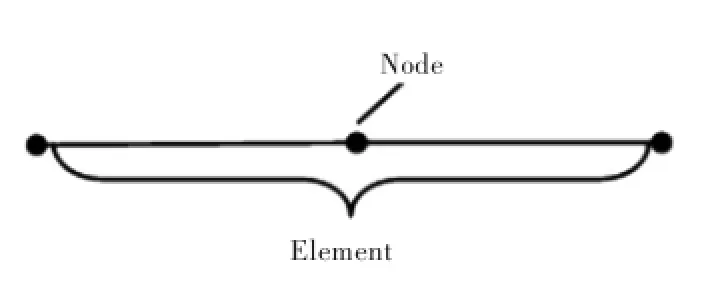
图2　常数单元示意图Fig.2　Constant element

此时，边界积分方程（2）便转为以下线性方程组：

或

对于节点（本例中为20个），线性方程组（3）可表示为如下矩阵形式：

式（5）中的系数矩阵H和G的计算方式如下：

1）当i=j时，场点P分布在单元内，位于单元节点的位置。因积分计算带有奇异点，按柯西主值积分，可以推导得到

式中，l为单元长度。

2）当i≠j时，

式中：hij和gij为场点在第i个单元时第j个单元产生的影响系数；R为场点P到源点Q的向量矢径；n为单元的单位法向量，指向方形区域外部。积分式（9）和式（10）采用4点高斯积分进行数值计算。本算例的计算结果如表1和表2所示。

在划分20个网格单元，采用常数单元离散，积分方法采用4点高斯积分公式的情况下：速度势的最大相对误差为5.225 4%，速度势的平均相对误差为1.365 3%，速度的最大相对误差为5.415 3%，速度的平均相对误差为2.491 2%。

表1　常数单元速度势计算结果Tab.1The calculation results of constant element velocity potential

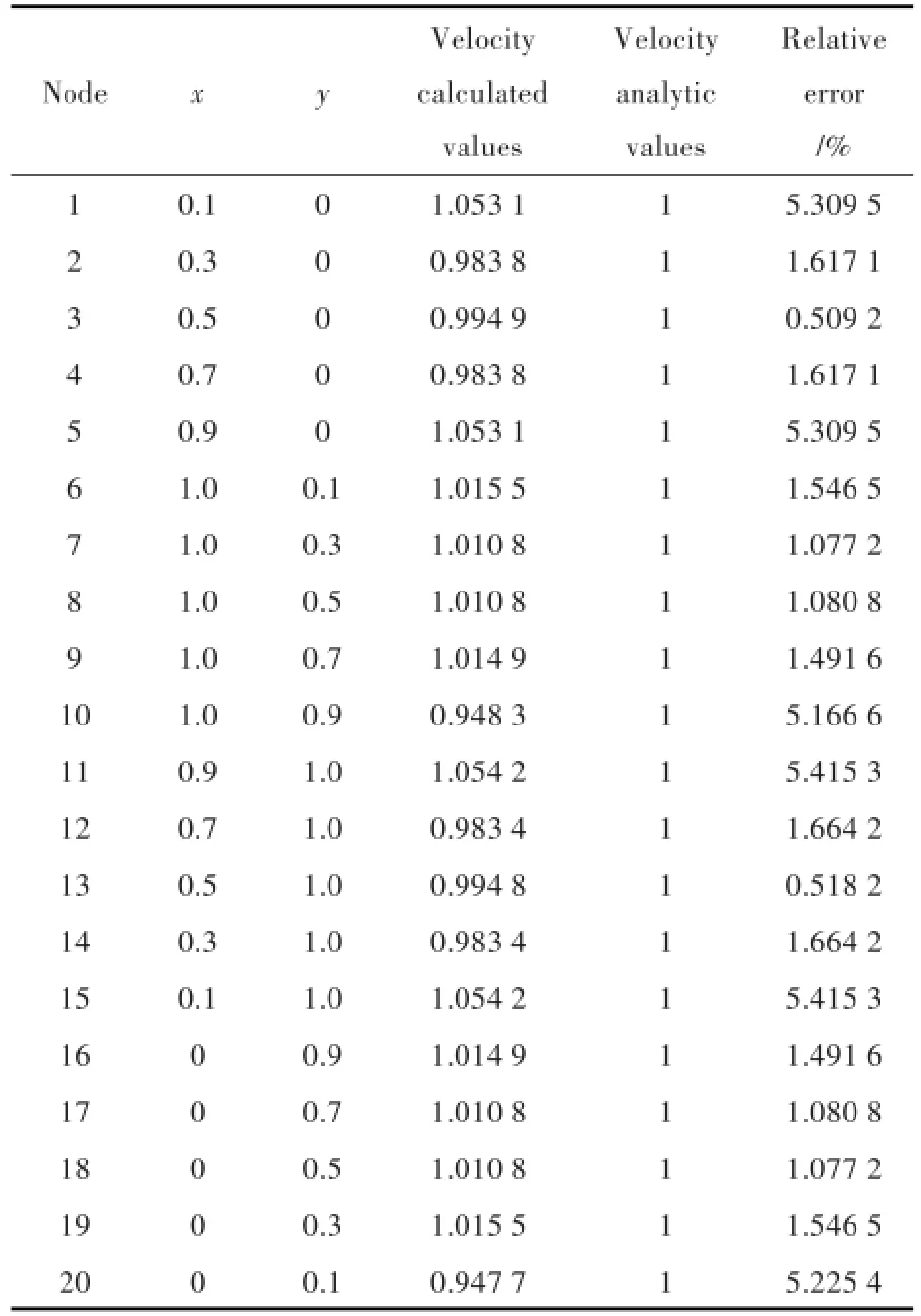
表2　常数单元速度计算结果Tab.2The calculation results of constant element velocity

1.2.2线性单元

对于线性单元，其节点设在单元端点处。如图3所示，将物理量在单元上进行线性插值处理，建立单元上任意点的函数值与单元节点的关系。

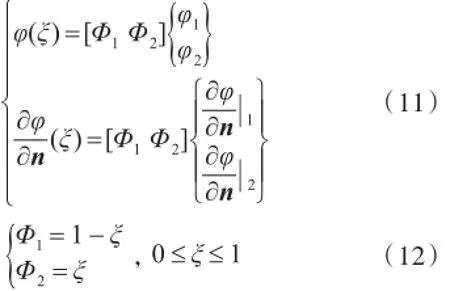
式中：ξ为边界元的局部坐标，首尾两节点的局部坐标值分别为0和1；φ1，φ2和分别为首尾两节点的值与值；Φ为插值基函数。

图3　计算影响系数时需代入边界条件的单元Fig.3　The element needing to concern boundary conditions when calculating the influence coefficients

将式（11）代入边界积分方程（2）并进行简化，得

其中：

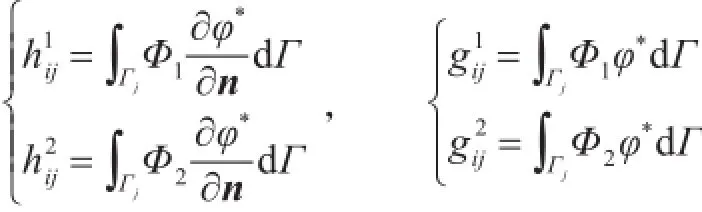
与常数单元类似，将式（13）简化成如式（5）一样的矩阵形式HU=GN后，代入已知边界条件，即可求解得出边界上未知的φ和

另需注意，对于线性单元，有些单元需进行特殊处理。如图3所示，对于本算例的角点单元：一个节点的已知条件属于本质边界条件，另一节点属于自然边界条件。对这样的单元做插值处理将会与已知条件冲突，因此在进行程序设计时需特别注意，否则，将导致这类单元节点的计算结果出现较大误差。

为便于与常数单元比较，积分方法依然选用高斯积分法，结果如表3和表4所示。

表3　线性单元速度势计算结果Tab.3The calculation results of linear element velocity potential

表4　线性单元速度计算结果Tab.4The calculation results of linear element velocity

在划分20个网格单元，采用线性单元离散，积分方法采用4点高斯积分公式的情况下：速度势的最大相对误差为0.543 9%，速度势的平均相对误差为0.137 3%，速度的最大相对误差为5.415 3%，速度的平均相对误差为2.491 2%。

1.3常数单元与线性单元比较

从以上结果可以看出，采用常数或线性单元的直接边界元法解势流速度场可以得出有效的计算结果。其误差主要是由高斯积分法近似引起，用Matlab工具箱中的int符号积分函数［7］可以提高精度，但运算效率较低。也可以通过使用更合适的数值积分方法来提高计算精度。

常数单元在数学处理和编程实现上都较为简便，在单元数相同的条件下，常数单元较线性单元精度低，但是可以通过增加单元数来提高计算精度。线性单元的节点设在单元边界上，需进行角点处理，因而对复杂边界的适应性不强。经权衡，初步认为总体上采用常数单元效率较高。

2　三维问题计算

2.1数学模型

考虑无穷远边界的流场［8-9］，有沿x轴负向的、速度为1的均匀来流。流体无旋、无粘性、不可压缩，流场中有一个半径为1的圆球。流场速度势可表示为

式中：Φ0为总速度势；V∞为无穷远处的来流速度；φ为圆球的扰动速度势。若直接求解Φ0，由于物面不可穿透条件，离散化之后的代数方程组为齐次线性方程组，不能得出唯一的非零解。因此，将求解的直接变量选择为扰动速度势φ，扰动速度势φ满足定解方程

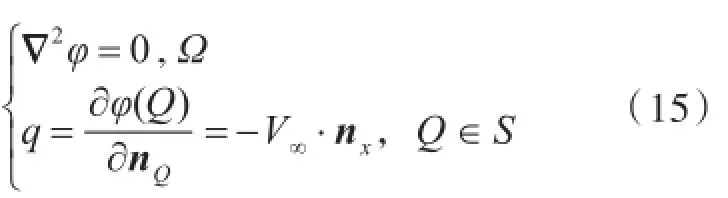
式中：Ω为流场区域；S为物面边界；nQ为Q点的单位法向量；nx为法向量在x轴上的分量。

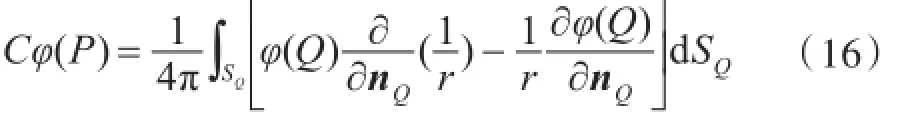
当边界光滑时，C（P）=1/2。

2.2离散与数值求解

（3）云计算技术的使用可以有效的提升各个采油厂的信息化水平，采油厂的信息化减少的投入和油田公司相差甚远，对此，就可以使用SaaS模式进行处理，构建采油厂的信息化平台，让油田公司的数据中心扮演采油厂的云服务商一角色，以各个采油厂的实际业务需求为基准，实行基础设施的托管服务以及SaaS系统服务。只有这样才可以更为高效且快速的去打造各类采油厂信息化的平台，从根源上满足采油厂的实际应用需求。

因三角形单元对复杂边界的适应性强，无需对物面的点进行坐标变换处理，所以选择将物面划分为三角形单元，如图4所示。由于三维问题的计算量比二维问题的大，为提高编程和运算效率，采用常数单元求解。

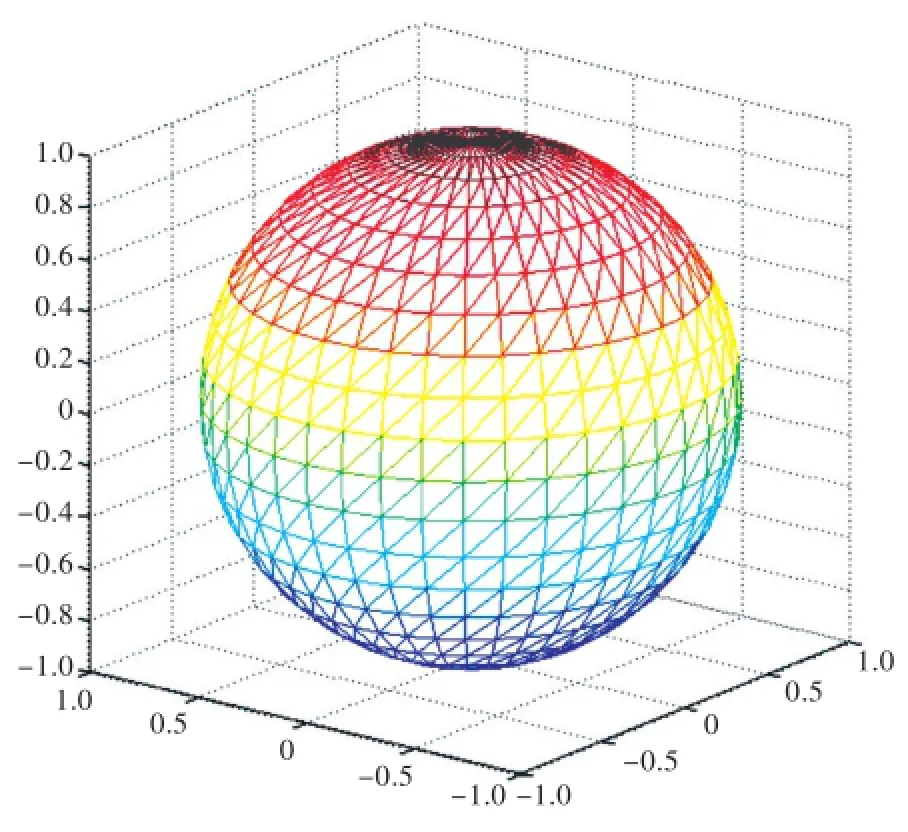
图4　圆球划分三角网格效果Fig.4　The effect of sphere divided into triangular meshes

由边界积分方程（16）离散得出线性方程组的过程与二维问题类似，见式（3）～式（5）。最后，简化为与式（5）一样的矩阵形式HU=GN，然后把边界条件·nx代入N中，即可求解得出圆球物面各个单元节点的速度势，进而可进一步求解出物面的速度场。

2.3系数矩阵与速度求解

影响系数矩阵的表达式和计算方法的说明如下：

1）当i=j时，场点P分布在单元内，涉及到高维奇异积分的处理。由于在单元内有，所以

方法1：采用3点高斯积分式。

因为奇点只在三角区域的中心处存在，而3点高斯积分法需要的积分点都是在三角形的边界上，所以避开了奇点。如图5所示。

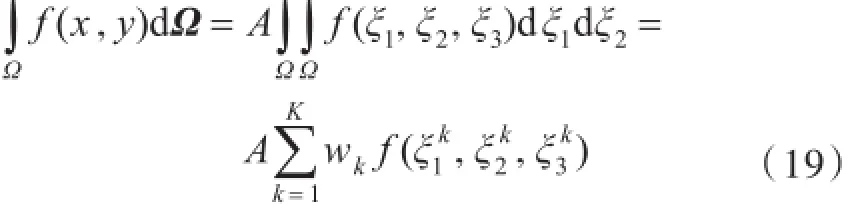
式中：f为被积函数；A为三角形区域的面积；w为权系数；ξ1，ξ2，ξ3为三角形面积坐标［1，10］。

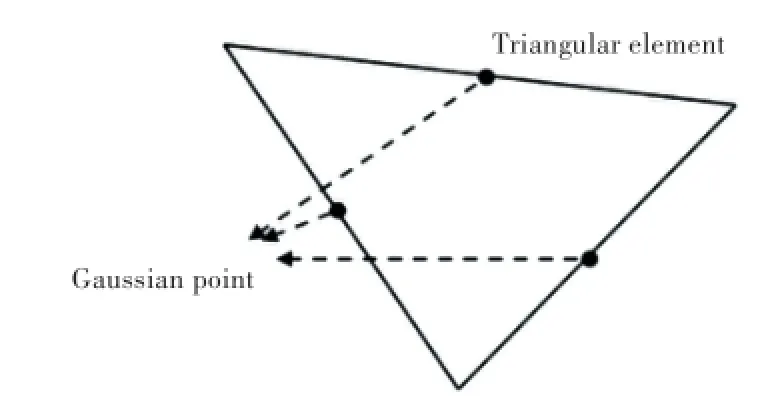
图5　高斯积分点示意图Fig.5　Sketch of Gauss integral points

方法2：采用在四边形上均匀分布奇点的诱导速度公式。

引入坐标系oξηζ，原点一般取在四边形ΔS的形心处，坐标平面ξηζ即为四边形ΔS所在平面，ζ轴的正向为ΔS的法线方向。ΔS的四个顶点p1，p2，p3，p4按逆时针方向排列，顶点pi的坐标为（ξi，ηi，0）（i=1，2，3，4）。奇点的坐标p的坐标为（x，y，z）。给出单层位势计算公式［5］：

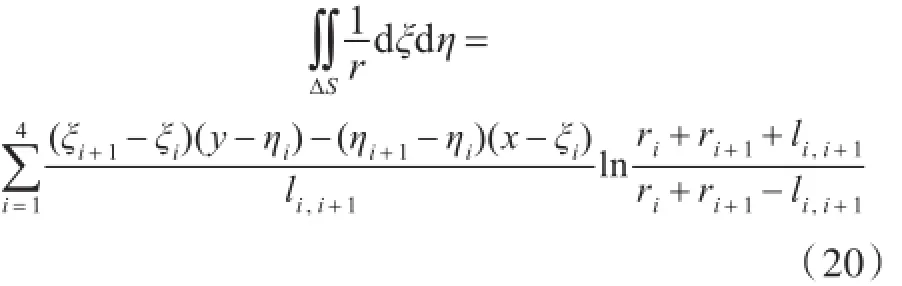
式中：li，j为四边形边长，其中i，j为顶点编号；ri为各顶点到奇点p的距离。

把三角形视为某两个顶点重合的四边形进行计算，发现与高斯积分法计算结果相比，其节点速度势最大误差提高了，平均误差降低了。

方法3：采用Matlab函数quad2d（）处理匿名函数积分［7］。

2009版以后的Matlab软件带有二重积分函数quad2d（），可以近似计算奇异积分，运算时的效率也挺高，但和高斯积分相比要慢。其精度与方法2的处理结果相近。

2）当i≠j时，

式中，n为单元的单位法向量，指向流场外部（物面内部）。该积分式因不含奇异性，故结果易收敛。

求得物面控制点处的势函数值后，文献［11］提供了一种简便的用数值微分方法计算物面上速度分布的方法。设物面方程为y=y（x，z），势函数在物面上的增量可以写成

式中：。在控制点附近任意找两点，两次使用式（23），便可求解出u*，w*。用下式求解速度矢量：

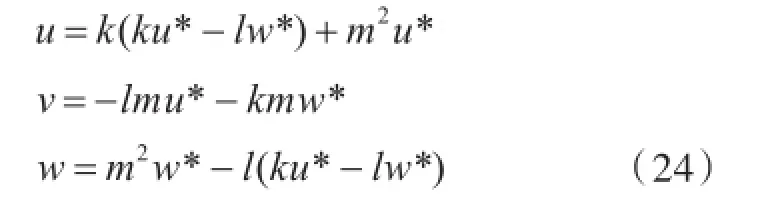
式中：u，v，w为控制点速度的3个分量；l，m，k为控制点单位法向量的3个分量。

由于单元数对计算结果的影响很大，故本文选取不同的单元数分别采用上述方法进行了试验。以7点的高斯积分法计算系数矩阵的结果如图6～图11所示。

当单元数为360时，速度势的最大误差为14.683 7%，平均误差为3.002 5%；速度的最大误差为12.750 0%，平均误差为2.080 0%。

基于网格的划分方法，球的两个极点附近的单元数较少，因而其误差较其它位置节点处的突出。由于所使用二维积分式的数值积分精度不高，因此三维问题的计算结果不如二维问题的好，可以考虑结合采用改进网格划分和数值积分的方法提高计算精度。

图6　360个网格速度势计算结果Fig.6　The velocity potential calculation results of 360 grids

图7　360个网格速度计算结果Fig.7　The velocity calculation results of 360 grids

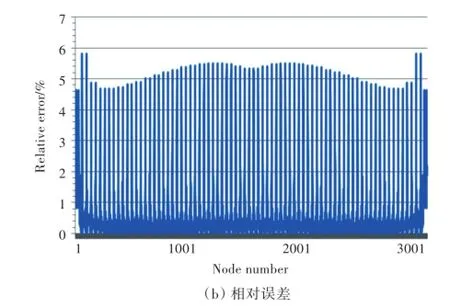
图9　 1230个网格速度势计算结果Fig.9　The velocity potential calculation results of 3 120 grids

图11　 3120个网格速度矢量Fig.11　The velocity vector results of 3 120 grids

图10　 3120个网格速度计算结果Fig.10　The velocity calculation results of 3 120 grids

图8　360个网格速度矢量Fig.8　The velocity vector results of 360 grids

速度幅值计算结果的精度是可以接受的，但该计算结果未能精确反映解析解给出的速度变化趋势，例如，驻点和速度最大值的位置未能精确反映出来。这主要是由数值计算误差所致，不仅物面速度计算存在误差，而且速度势函数计算本身也存在误差。

当单元数为3 120个时，速度势最大误差为5.807 8%，平均误差为0.621 8%；速度最大误差为7.090 0%，平均误差为0.120 0%。随着单元数的增加，计算精度显著提高。

3　结语

对应用于船舶水动力学数值计算中的边界元法，多采用以Hess-smith方法为基础的间接边界元法。Hess-smith方法是先求解各单元的源强密度，使其与系数矩阵相乘而得到速度势，由于其借助了作为中间变量的源强密度，从而使得这类间接边界元法在编程和计算效率上不如直接边界元法。另外，相对于间接边界元法，直接边界元法的数学意义更严谨，物理意义更明确。

边界元法的计算量主要集中在影响系数矩阵的计算上，误差也大多源于此。本文对多种数值积分方法进行了数值试验，分析了各种方法对最终结果误差的影响。改进本文方法或使用精度更高的数值积分算法，是提高计算结果精度的重要途径。

本文研究了无限域的势流问题，通过求解经典算例并与解析解的比较，证明了采用直接边界元法求解船舶水动力学势流绕流问题的可行性。直接边界元法的数值计算和程序设计过程具有通用性，适用于任何无限域三维势流的速度势和速度的求解。若进一步引入兴波条件和多片体干扰效应等，还可求解更广泛的船舶水动力学势流绕流数值计算问题。

［1］王元淳.边界元法基础［M］.上海：上海交通大学出版社，1988：6-33.

［2］姚寿广.边界元数值方法及其工程应用［M］.北京：国防工业出版社，1995：1-24.

［3］邓小敏.多体船计算及船型优化研究［D］.大连：大连理工大学，2012.

［4］李子如.用面元法预报船体兴波阻力［D］.武汉：武汉理工大学，2006.

［5］戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京：国防工业出版社，2008：24-28.

［6］张兆顺，崔桂香.流体力学［M］.2版.北京：清华大学出版社，2006：130-131.

［7］陈泽，占海明.详解MATLAB在科学计算中的应用［M］.北京：电子工业出版社，2011.

［8］余灵，李干洛.球尾渔船表面流场的数值计算［J］.华南理工学报（自然科学版），1995，23（10）：155-163. YU Ling，LI Ganluo.Numerical calculation of flow fields over ship hulls of bulbous stern fishing boat［J］. Journal of South China University of Technology（Natu⁃ral Science），1995，23（10）：155-163.

［9］余灵，李干洛，羊少刚.船体表面流场的理论计算与数值分析［J］.广东造船，1994（3）：1-7.

［10］HIRSCH C.Numerical computation of internal and external flows［M］.2nd ed.Butterworth-Heinemann，2007：221-223.

［11］王献孚.计算船舶流体力学［M］.上海：上海交通大学，1992：244-245.

［责任编辑：卢圣芳］

Direct Boundary Element Method for the Problem of Potential Flow Velocity Field

LI Jingyu，LU Xiaoping，ZHAO Pengwei
Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

In the field of ship hydrodynamics，scholars usually adopt Hess-Smith method to solve the po⁃tential flow problem.However，this method is essentially based on the physical intuition，and there are shortcomings concerning this theory in numerical calculation.Since the direct boundary element method is rarely used in ship hydrodynamic problems，the presented method in this paper has broad application pros⁃pects in the field of ship hydrodynamics and may promote the direct boundary element method.According to the boundary integral method，an integral equation is established to solve the unbounded potential flow problem，and the flow field velocity distribution on the surface of the velocity potential is then obtained.A comparison with the analytical solution is finally conducted for error analysis.In this paper，both 2D and 3D numerical examples are provided and programmed to realize the numerical calculation process in Mat⁃lab.The results show that the direct boundary element method has decent precision and efficiency，and the numerical implementation is even more concise.Moreover，this method can be developed into general forms to solve other ship dynamic problems.

direct boundary element method；potential flow theory；numerical integration；ship hydrody⁃namics

中国分类号：U661.1A

10.3969/j.issn.1673-3185.2015.01.010

2014-08-18

网络出版时间：2015-1-28 12:01

国家部委基金资助项目

李井煜，男，1990年生，硕士生。研究方向：舰船流体动力性能。E⁃mail：935228691@qq.com

卢晓平（通信作者），男，1957年生，博士，教授。研究方向：舰船流体动力性能