大跨度空腹夹层板楼盖的静力稳定性分析*
2015-08-27张瑞鹏马克俭刘卓群杨志勇孙敬明华建坤
张瑞鹏,马克俭 ,刘卓群,杨志勇,孙敬明,华建坤,张 震
(贵州大学 空间结构研究中心,贵州 贵阳550003)
钢筋混凝土空腹夹层板结构称为“剪力键双向空心大板”,它是由上、下两层井字格带肋板组成,并在井字格交叉处用宽度大于高度的剪力键联结而成。空腹夹层板楼盖体系是大跨度空间结构常用的结构形式,是一种新型空间网格板,它克服了空腹网架抗剪刚度差的缺点,同时还保持了空腹网架结构的优点,具有广泛的用途[1]。
空腹夹层板楼盖结构自1995 年被马克俭教授等人提出后,这类新型结构引起众多学者的广泛关注。目前对空腹夹层板结构的静力性能研究文献较少,文献[2]对空腹夹层板的整体挠度、剪力键变形和上下肋变形做了基础性研究,了解到空腹夹层板的相关的静力性能和实用的计算方法。文献[3]对空腹夹层板的自振特性进行了研究,明白了空腹夹层板的自振特性。为了进一步掌握空腹夹层板的静力稳定性,本文采用基于ANSYS 的线性有限元法进行分析,得出了空腹夹层板的静力稳定性的特点。
1 计算模型及参数分析方案
本文的计算模型为大跨度钢筋混凝土空腹夹层板楼盖,采用24 m ×24 m 周边柱网支撑的正交正放空腹夹层板楼盖结构进行研究,各边每隔6 m按柱子的布置原则设置一个刚性连接,平面布置图如图1 所示,剖面如图2 所示,ANSYS 有限元模型如图3 所示。钢筋混凝土空腹夹层板静力稳定性的影响因素主要有空腹夹层板厚度、表层薄板的厚度和上下肋的高度,文中的参数化分析主要基于以上三种参数进行。采用ANSYS 有限元软件进行分析时,对空腹夹层板的所有构件均采用实体单元建模,混凝土材料的密度为2500 kg/m3,弹性模量为3 ×104N/mm2,泊松比为0.2,钢筋采用HRB400。
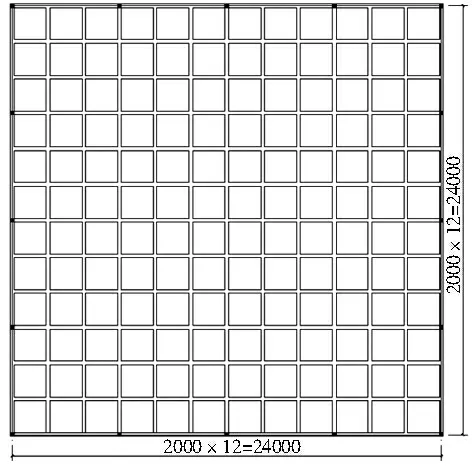
图1 空腹夹层板平面布置图

图2 空腹夹层板剖面图

图3 空腹夹层板有限元模型
2 静力稳定性分析
2.1 分析方法
静力稳定性分析对于研究空腹夹层板楼盖体系的静力性能具有重要意义,结构失稳(屈曲)是指在外力作用下结构的平衡状态开始丧失,稍有扰动变形便迅速增大,最后使结构发生破坏。特征值屈曲分析是理想化情况下的分析,即结构达到某种荷载时,除结构原来的平衡状态存在外,还可能出现第二个平衡状态,所以又称为平衡分岔失稳或分支点失稳,此类结构失稳时相应的荷载称为屈曲荷载[4]。本文主要对空腹夹层板楼盖结构体系的特征值屈曲进行一定的研究分析,并可为研究其非线性屈曲分析和工程应用提供一定的参考。
2.2 空腹夹层板结构的特征值屈曲模态
分析模型取空腹夹层板厚度900 mm,上下肋截面尺寸为400 mm×250 mm,剪力键尺寸取400 mm×400 mm,网格尺寸为2000 mm,板厚为100 mm。该模型的前六阶屈曲模态如图4 所示,前六阶屈曲荷载值如图5 所示,从结果可以看出,空腹夹层板的第一阶屈曲模态为整体变形,后几阶屈曲模态以大面积局部屈曲为主,说明该结构的整体刚度比较好,静力稳定性较好。
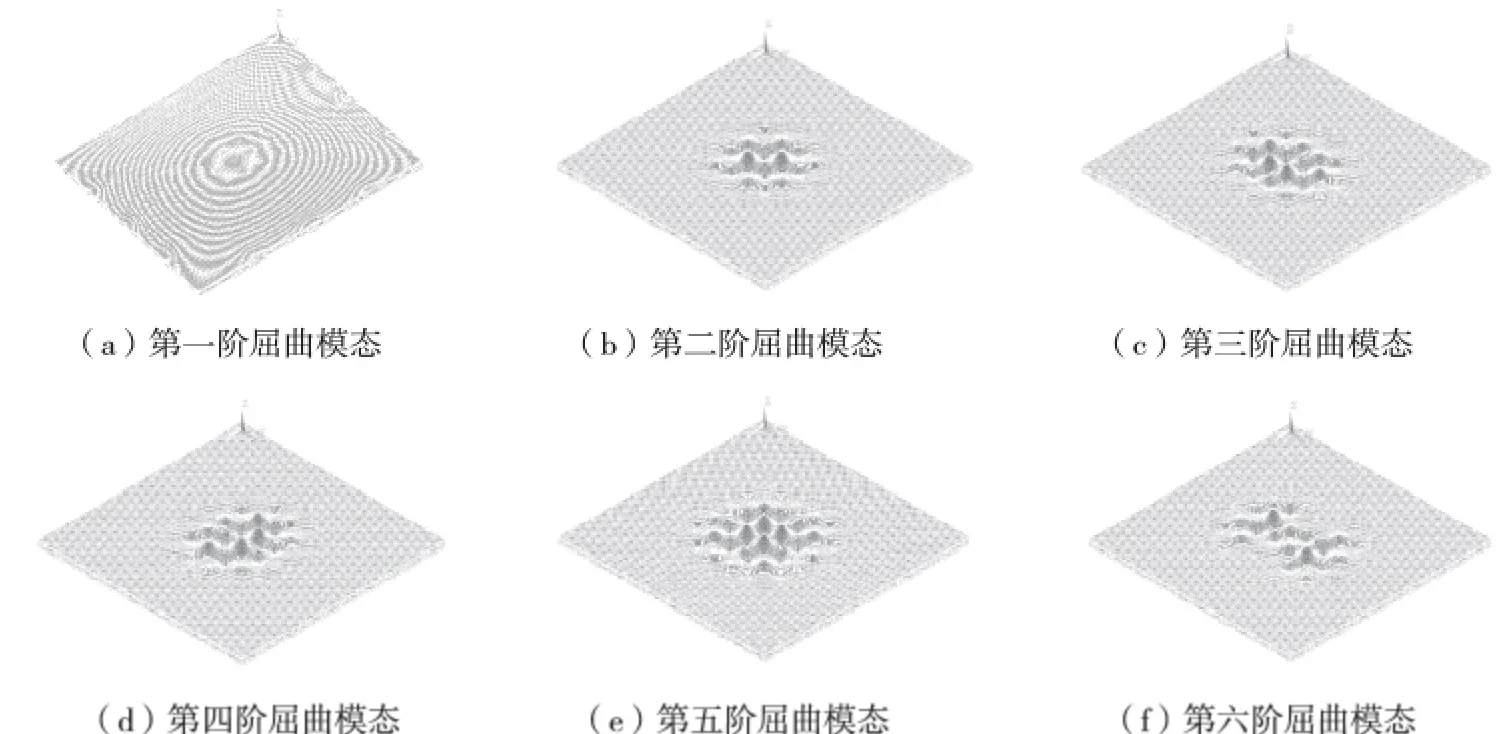
图4 钢筋混凝土空腹夹层板前六阶特征值屈曲模态
2.3 特征值屈曲的参数化分析
2.3.1 钢筋混凝土空腹夹层板厚度对特征值屈曲的影响
各分析模型取空腹夹层板上下肋截面尺寸为400 mm×250 mm,剪力键尺寸取400 mm ×400 mm,网格尺寸为2000 mm,板厚为100 mm。在此基础上保证其他条件不变,空腹夹层板厚度取值由800 mm起按照50 的增量增加到1000 mm,共5 个计算模型。各个模型的前六阶特征值屈曲荷载值如图6 所示,特征值屈曲荷载值随着空腹夹层板的厚度增加而明显增大。以第一阶屈曲荷载值为例,空腹夹层板厚度由800 mm 变为1000 mm 时,相应荷载值由129.78 kN/m2增加到173.52 kN/m2,荷载值增大43.74 kN/m2,数值增加幅度为33.7%,表明增加空腹夹层板的厚度可以显著提高其静力稳定性,提高其特征值屈曲荷载值。

图5 前六阶特征值屈曲荷载值
2.3.2 钢筋混凝土空腹夹层板上下肋高度对特征值屈曲的影响
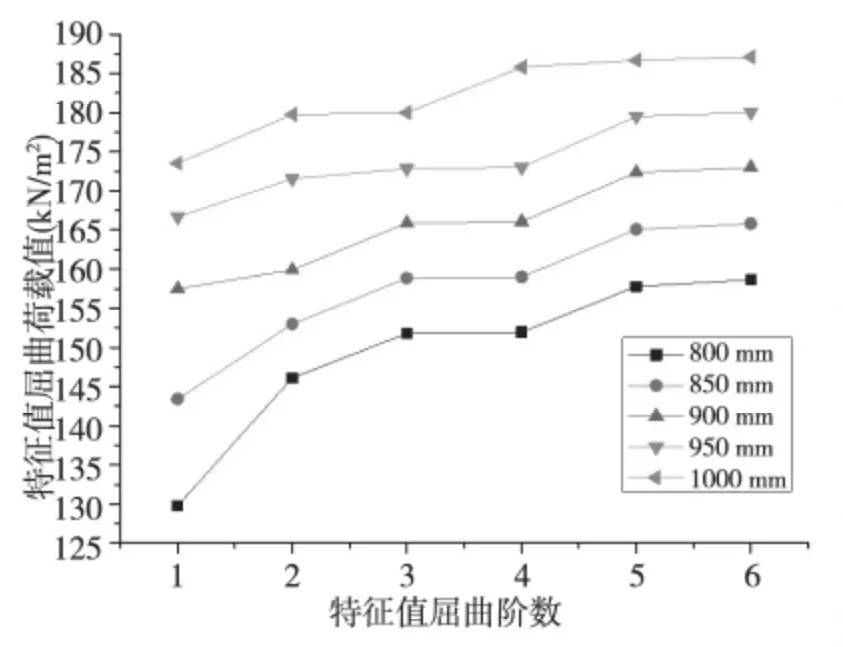
图6 空腹夹层板板厚与屈曲荷载关系图
各分析模型的空腹夹层板厚度取900 mm,上下肋截面尺寸宽度为400 mm,剪力键尺寸取400 mm×400 mm,网格尺寸为2000 mm,板厚为100 mm,高度由200 mm 起按照10 mm 的增量增大到300 mm,共11 个计算模型。各模型的前六阶特征值屈曲荷载值如图7 所示,屈曲荷载值随着空腹夹层板上下肋高度的增加先增大到一定程度,然后又稍有下降。以第一屈曲荷载值为例,当上下肋高度由200 mm 增加到270 mm 时,相应屈曲荷载值由123.6 kN/m2增大到160.82 kN/m2,荷载值增大37.22 kN/m2,数值增加幅度为30.1%。当上下肋高度由270 mm 增加到300 mm 时,数值由160.82 kN/m2下降到159.94 kN/m2,荷载值减小0.88 kN/m2。以上数据表明,适当增大空腹夹层板上下肋的高度可提高其特征值屈曲荷载,当高度达到一定程度后继续加大时,空腹夹层板的特征值屈曲荷载值将稍微减小,工程中应该选用适当的上下肋高度值以提高结构的屈曲荷载和静力稳定性。

图7 上下肋高度与屈曲荷载关系图
2.3.3 钢筋混凝土空腹夹层板表层薄板厚度对特征值屈曲的影响

图8 表层薄板厚度与屈曲荷载关系图
各分析模型取空腹夹层板厚度取900 mm,上下肋截面尺寸为400 mm×250 mm,剪力键尺寸取400 mm ×400 mm,网格尺寸为2000 mm,表层薄板厚度分部取值为60 mm、80 mm、90 mm、100 mm、110 mm、120 mm 和140 mm,共7 个计算模型。各模型的前六阶特征值屈曲荷载值如图8 所示,屈曲荷载值随着空腹夹层板上下肋高度的增加开始时显著增大,当增大到一定程度后,又有较大的下降。以第一屈曲荷载值为例,当表层薄板厚度由60 mm增大到100 mm 时,相应荷载值由57.05 kN/m2增大到157.48 kN/m2,荷载值增大100.43 kN/m2,数值增加幅度为175.98%。当表层薄板厚度由100 mm增大到140 mm 时,相应荷载值由157.48 kN/m2下降到144.05 kN/m2,荷载值下降了13.43 kN/m2,数值下降幅度为8.53%。综上所述,空腹夹层板特征值屈曲荷载随着表层薄板厚度的增加而先增大后减小,厚度取跨度的1/24 时其特征值屈曲荷值较大,静力稳定性较好。
3 结论
本文通过用ANSYS 有限元软件对空腹夹层板的特征值屈曲分析,得出结论如下:
(1)空腹夹层板特征值屈曲以整体变形为主,其次为大面积局部屈曲为主,结构的整体刚度较好,静力稳定性较好。
(2)空腹夹层板厚度的增加可以显著提高其静力稳定性,特征值屈曲荷载值也明显增大。
(3)空腹夹层板的上下肋高度适当增大可提高其特征值屈曲荷载,但高度达到一定程度后继续加大时,其特征值屈曲荷载值将减小,静力稳定性将变差。
(4)空腹夹层板的特征值屈曲荷载随表层薄板厚度的增加而先增大后减小,建议取跨度的1/24,其特征值屈曲荷载和结构的静力稳定性较好。
[1]马克俭,张华刚,郑涛. 新型建筑空间网格结构理论与实践[M].北京:人民交通出版社,2006.
[2]张华刚,马克俭.空腹夹层板刚度分析的简化算法及其静力性能分析[J].贵州工业大学学报:自然科学版,2003,32(5):66-71.
[3]钟永力,张华刚,马克俭. 空腹夹层板的自振特性分析[J]. 贵州大学学报:自然科学版,2014,31(1):104 -107.
[4]北京金木土软件技术有限公司. SAP2000 中文版使用指南[M].北京:人民交通出版社,2011.
